
Криволинейные интегралы - определение и вычисление с примерами решения
Содержание:
Криволинейные интегралы
Криволинейный интеграл первого рода
Пусть К — некоторая гладкая (или кусочно-гладкая) плоская кривая
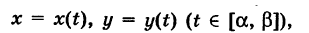
где t — параметр, а
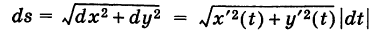
— ее дифференциал дуги. Здесь если 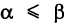 , то dt > 0 и
, то dt > 0 и 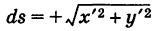 ; если же
; если же 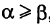 , то dt < 0 и
, то dt < 0 и 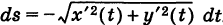 . Если
. Если 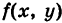 — функция, непрерывная на кривой К, то под ее криволинейным интегралом первого рода, взятым по кривой понимается интеграл
— функция, непрерывная на кривой К, то под ее криволинейным интегралом первого рода, взятым по кривой понимается интеграл
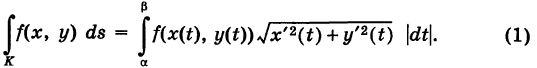
Если кривая 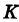 задана уравнением
задана уравнением
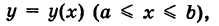
то, рассматривая х как параметр, получим
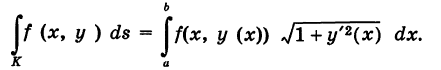
Допустим, что кривая К — материальная, т. е. имеет массу. Пусть 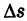 — некоторая дуга кривой К, содержащая точку М, а
— некоторая дуга кривой К, содержащая точку М, а 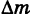 — масса этой дуги. Тогда отношение
— масса этой дуги. Тогда отношение 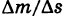 носит название средней плотности дуги
носит название средней плотности дуги 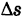 , а
, а
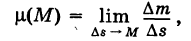
т. е предел средней плотности дуги при условии, что дуга 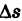 стягивается в точку М, называется линейной плотностью дуги в точке М.
стягивается в точку М, называется линейной плотностью дуги в точке М.
Если 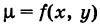 рассматривать как линейную плотность дуги в текущей ее точке М (х, у), то
рассматривать как линейную плотность дуги в текущей ее точке М (х, у), то
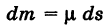
есть масса бесконечно малой дуги ds (элементарная масса) и интеграл

представляет собой массу линии (физический смысл криволинейного интеграла первого рода).
Криволинейный интеграл первого рода обладает следующими очевидными свойствами.
1) При изменении направления интегрирования криволинейный интеграл первого рода не изменяет своего значения (рис. 238), т. е.
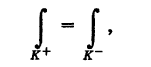
где К+ — кривая К, пробегаемая в заданном направлении (например, при возрастании параметра t), а К-— кривая К, пробегаемая в противоположном направлении (соответственно при убывании t).
2) Если кривая интегрирования К с помощью некоторой точки разбита на части: 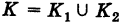 (рис. 238), то
(рис. 238), то
Пример:
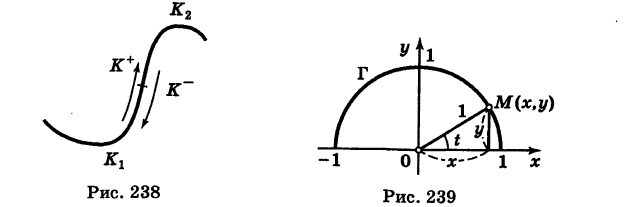
Найти массу полуокружности  (рис. 239), если линейная плотность ее в текущей точке М (х, у) пропорциональна ординате у.
(рис. 239), если линейная плотность ее в текущей точке М (х, у) пропорциональна ординате у.
Решение:
Беря в качестве параметра t полярный угол (рис. 239), получаем параметрические уравнения полуокружности
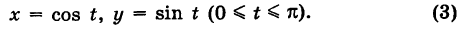
Элементарная масса
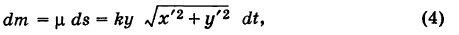
где k — коэффициент пропорциональности. Так как
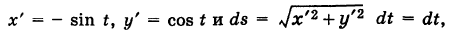
то из (4) имеем
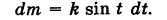
Отсюда масса линии Г будет равна
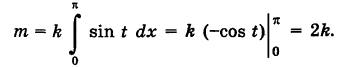
Аналогично определяется криволинейный интеграл первого рода от функции f(x, у, z), взятый по кусочно-гладкой пространственной кривой К:
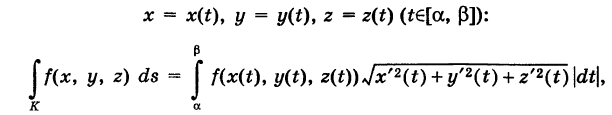
где
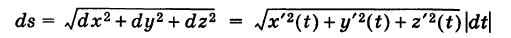
— дифференциал дуги пространственной кривой -К.
Криволинейный интеграл второго рода
Пусть
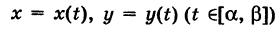
— гладкая (или кусочно-гладкая) кривая К с выбранным направлением (такую линию, для краткости, будем называть путем) и Х(х, у), Y (х, у) — пара функций, непрерывных на кривой К. Учитывая, что дифференциалы текущих координат х и у кривой К имеют вид
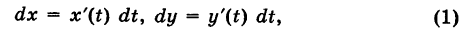
под криволинейным интегралом второго рода от пары функций X и Y, взятым по кривой К, понимается интеграл
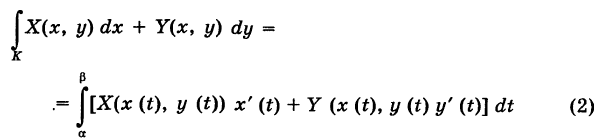
(по традиции для выражения, стоящего слева, скобки не пишутся и предполагается, что интеграл  относится ко всей сумме).
относится ко всей сумме).
Если путь К задается уравнением 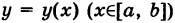 , то формула (2) принимает вид
, то формула (2) принимает вид
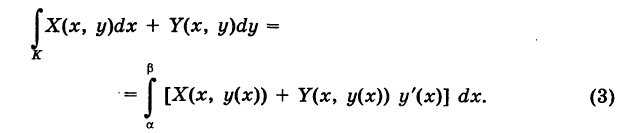
Аналогично, если K, задается уравнением 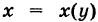
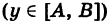 , то
, то
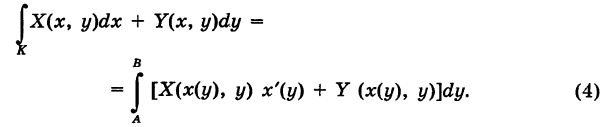
Криволинейный интеграл второго рода обладает следующими свойствами.
1) При изменении направления пути интегрирования криволинейный интеграл второго рода изменяет свой знак на обратный, т. е

Действительно, изменение направления пути интегрирования равносильно перестановке пределов интегрирования 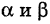 в определенном интеграле (2); а это влечет изменение знака определенного интеграла.
в определенном интеграле (2); а это влечет изменение знака определенного интеграла.
2) Если путь интегрирования К состоит из двух частей К = 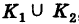 , то
, то

Пример:
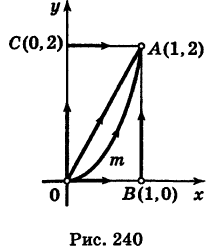
Найти значения интеграла 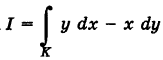 вдоль указанных путей: 1) OA — прямая; 2)
вдоль указанных путей: 1) OA — прямая; 2) 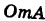 — парабола с вершиной О и осью Оу; 3) ОВА — ломаная, 4) ОСА — ломаная (рис. 240).
— парабола с вершиной О и осью Оу; 3) ОВА — ломаная, 4) ОСА — ломаная (рис. 240).
Решение:
1) Уравнение прямой OA есть у = 2х 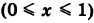 . Отсюда dy = 2 dx и, следовательно,
. Отсюда dy = 2 dx и, следовательно,
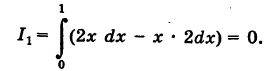
2) Уравнение параболы  имеет вид у = kx2. Так как парабола проходит через точку
имеет вид у = kx2. Так как парабола проходит через точку 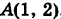 , то 2 = k - 12 и, значит, k = 2, т. е. у = 2х2. Отсюда dу = 4х dx и
, то 2 = k - 12 и, значит, k = 2, т. е. у = 2х2. Отсюда dу = 4х dx и
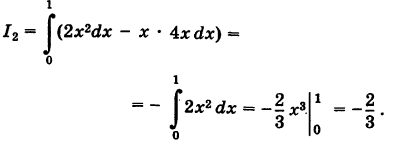
3) На основании свойства 2 имеем
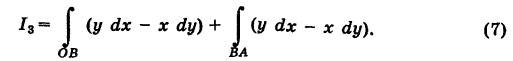
Так как уравнение ОВ есть у = 0 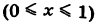 , то
, то 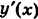 = 0. Далее, уравнение ВА записывается так: х = 1
= 0. Далее, уравнение ВА записывается так: х = 1 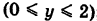 ; поэтому х'(у) = 0. Из формулы (7) получаем
; поэтому х'(у) = 0. Из формулы (7) получаем
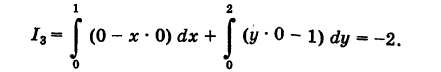
4) Аналогично,
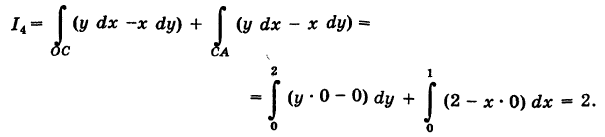
Заметим, что здесь интеграл I при фиксированных концах пути интегрирования К зависит от вида этого пути.
Пример:
Найти
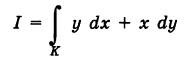
вдоль линий К, указанных в примере 1.
Воспользовавшись приведенными выше уравнениями линии К, последовательно имеем:
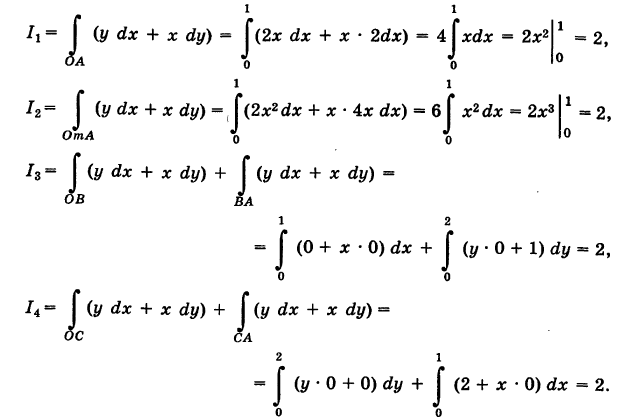
Таким образом, здесь интеграл I имеет одно и то же значение для различных путей, соединяющих точки О и А. Принципиальное различие примеров 1 и 2 будет разъяснено. Если
есть кусочно-гладкая пространственная кривая 
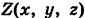 — тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл
— тройка функций, непрерывных на кривой К, то под соответствующим криволинейным интегралом второго рода понимается интеграл
Физический смысл криволинейного интеграла второго рода
Пусть 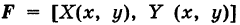 — непрерывно меняющаяся переменная сила и
— непрерывно меняющаяся переменная сила и
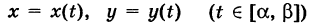
— путь К, пробегаемый точкой ее приложения (рис. 241); обозначим через 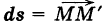 бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку
бесконечно малый вектор перемещения из текущей точки М (х, у) кривой К в бесконечно близкую точку 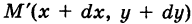 (мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = {dx, dy}. Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна
(мы здесь пренебрегаем бесконечно малыми высшего порядка по сравнению с ds). Имеем ds = {dx, dy}. Так как на бесконечно малом пути ds непрерывную силу F можно считать постоянной, то элементарная работа силы равна
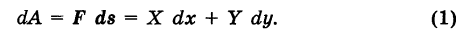
Интегрируя выражение (1) вдоль кривой К, получим работу силы
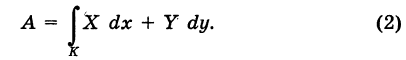
Выражение (2), очевидно, есть соответствующий криволинейный интеграл второго рода.
Итак, криволинейный интеграл второго рода представляет собой работу переменной силы вдоль пути интегрирования, проекциями которой на координатные оси являются соответствующие коэффициенты при дифференциалах переменных.
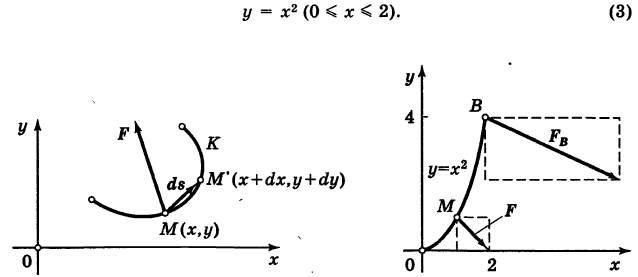
Пример:
Найти работу А переменной силы  , точка приложения которой описывает параболу ОВ (рис. 242)
, точка приложения которой описывает параболу ОВ (рис. 242)
Решение:
Согласно формуле (2) имеем
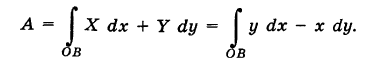
Из уравнения (3) получаем dy = 2х dx, поэтому
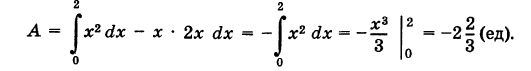
Аналогично, работа пространственной силы
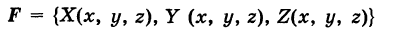
вдоль пути К: 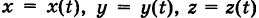 выражается криволинейным интегралом второго рода
выражается криволинейным интегралом второго рода
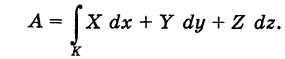
Условие независимости криволинейного интеграла второго рода от вида пути интегрирования
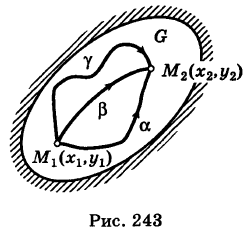
Пусть 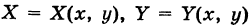 — непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки
— непрерывные функции в области G (рис. 243). Рассмотрим две произвольные точки 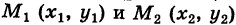 области и всевозможные пути
области и всевозможные пути 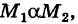
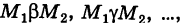 соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что
соединяющие эти точки (М1 — начало пути, М2 — конец пути) и не выходящие за пределы области G. Может случиться, что
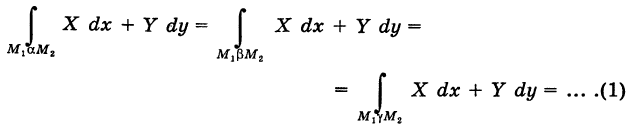
В таком случае говорят, что криволинейный интеграл второго рода
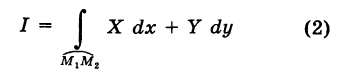
не зависит от вида пути интегрирования в данной области G.
Если выполняются условия (1), то для интеграла (2) нет необходимости указывать путь интегрирования, а достаточно отметить лишь его начальную точку  и его конечную точку М2
и его конечную точку М2 пути. Поэтому здесь употребляется обозначение
пути. Поэтому здесь употребляется обозначение
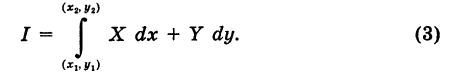
Справедлива следующая теорема:
Теорема: Если в области G подынтегральное выражение X dx + Y dy является полным дифференциалом некоторой функции U = U (х, у), т. е.
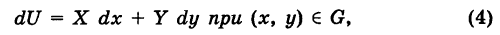
то криволинейный интеграл (2) не зависит от пути интегрирования в области G.
Доказательство: Пусть
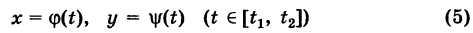
— произвольный путь К в области G, соединяющий точки 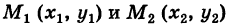 , причем
, причем
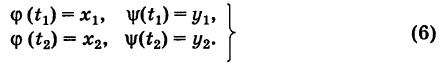
Из формулы (4) имеем
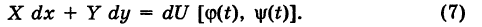
Отсюда получаем
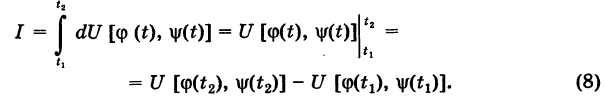
Далее, используя соотношения (6), будем иметь
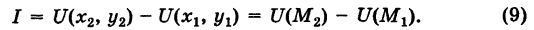
Таким образом, значение интеграла I одно и то же при любом выборе функций 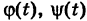 , и, следовательно, интеграл I не зависит от вида пути, соединяющего точки
, и, следовательно, интеграл I не зависит от вида пути, соединяющего точки 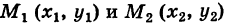
Следствие 1. Если выполнено соотношение (4), то в силу (9) имеем
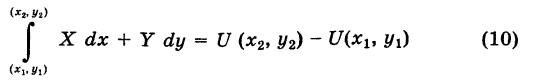
(обобщенная формула Ньютона — Лейбница).
Следствие 2. Если подынтегральное выражение X dx + Y dy есть полный дифференциал и путь интегрирования К замкнутый, то
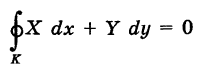
(кружок при интеграле обозначает интегрирование вдоль замкнутого пути).
Пример:
Найти
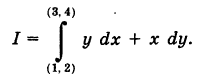
Решение:
Так как у dx + х dy = d (ху), то, независимо от вида пути, соединяющего точки 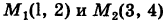 , имеем
, имеем
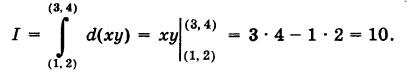
Работа потенциальной силы
Теорема предыдущего параграфа имеет физическое содержание. Пусть в области G определено силовое поле
Примером силового поля может служить поле силы тяжести у поверхности Земли, где на любую материальную точку массы т действует сила mg (g — ускорение свободного падения). Более общим примером силового поля является гравитационное поле, создаваемое массой М. Здесь на материальную точку массы 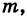 находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила
находящуюся на расстоянии г от притягивающего центра, согласно закону Ньютона действует сила 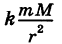 (k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.
(k — гравитационная постоянная), направленная к притягивающему центру. Другим примером силового поля служит электрическое поле Кулона.
Если существует функция 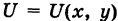 такая, что
такая, что
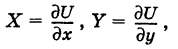
то говорят, что поле потенциальное (иначе, F — потенциальная сила), а функцию U называют потенциалом поля. В этом случае, очевидно,
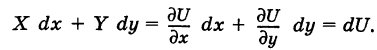
Отсюда для работы А потенциальной силы F вдоль пути, соединяющего точки 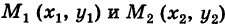 , имеем
, имеем
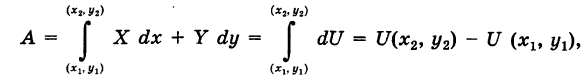
т. е. работа потенциальной силы не зависит от вида пути и равна разности потенциалов силы для конечной и начальной точек пути.
В частности, если путь замкнут, то работа А = 0.
Пример:
Найти работу А силы тяжести при перемещении в вертикальной плоскости Оху (вблизи поверхности Земли) точки массы т из положения 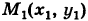 в положение
в положение 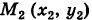 (рис. 244).
(рис. 244).
Решение:
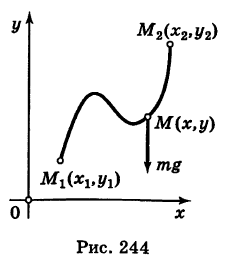
Если ось Ох горизонтальна, а ось Оу вертикальна, то проекции силы тяжести, действующей на материальную точку массы т, равны X = 0, У = -mg. Имеем
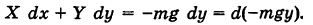
Поэтому за потенциал поля силы тяжести можно принять
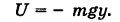
Отсюда работа силы тяжести, независимо от пути 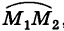 , равна
, равна
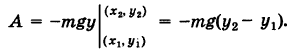
Замечание. Аналогичные результаты справедливы для криволинейного интеграла, взятого по пространственной кривой. В частности, если
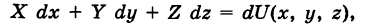
то
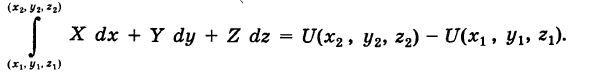
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |