
Криволинейное движение в физике - формулы и определения с примерами
Криволинейное движение:
Мы изучили прямолинейное движение — равномерное и равнопеременное. Криволинейное движение (рис. 88, а, б) встречается гораздо чаще. Каковы закономерности такого движения?
Пусть тело движется по криволинейной траектории, изображенной на рисунке 88, в. Ее (как и любую другую) можно приближенно разбить на прямолинейные участки 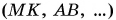
Прямолинейное движение мы изучили. Рассмотрим теперь движение тела (считая его материальной точкой) по окружности (рис. 89).

Чтобы охарактеризовать положение тела, проводят вектор 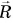 из центра окружности в ту точку траектории, где в данный момент это тело находится. Вектор
из центра окружности в ту точку траектории, где в данный момент это тело находится. Вектор 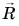 называют радиус-вектором.
называют радиус-вектором.
На рисунке 89 радиус-вектор 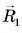 указывает, где находится тело в момент времени
указывает, где находится тело в момент времени 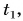 а радиус-вектор
а радиус-вектор 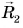 — в момент
— в момент 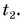
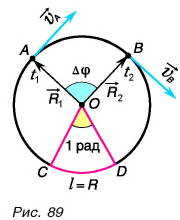
Тело движется по окружности, а радиус-вектор совершает вращательное движение. За время 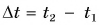 тело пройдет путь, равный длине дуги АВ, а радиус-вектор повернется на угол
тело пройдет путь, равный длине дуги АВ, а радиус-вектор повернется на угол 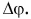
В СИ угол поворота измеряется в радианах (сокращенно — рад). Угол в 1 рад — это центральный угол, длина дуги которого равна радиусу окружности (рис. 89, угол СОD)).
Значит, если тело пройдет но окружности путь s, то угол поворота 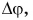 выраженный в радианах, будет равен
выраженный в радианах, будет равен

Для одного полного оборота по окружности путь 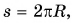 а угол поворота
а угол поворота 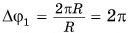 рад. Значит,
рад. Значит, 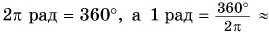
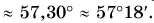
Двигаясь по траектории, в каждый момент времени тело имеет мгновенную скорость 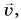 направленную по касательной к окружности (рис. 89). При рассмотрении движения но окружности ее принято называть линейной скоростью.
направленную по касательной к окружности (рис. 89). При рассмотрении движения но окружности ее принято называть линейной скоростью.
Рассмотрим самое простое из криволинейных движений — дви женив по окружности, при котором за любые равные промежутки времени тело (материальная точка) проходит одинаковые пути. В этом случае модуль линейной скорости 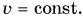 Однако скорость движения
Однако скорость движения 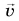 как векторная величина непостоянна
как векторная величина непостоянна 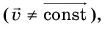 т. к. ее направление непрерывно изменяется (рис. 89).
т. к. ее направление непрерывно изменяется (рис. 89).
При движении по окружности со скоростью, модуль которой 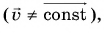 его радиус-вектор
его радиус-вектор 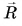 совершает равномерное вращение. Быстроту вращательного движения характеризуют угловой скоростью. Ее обозначают буквой со (омега). При равномерном вращении угловая скорость равна отношению угла поворота
совершает равномерное вращение. Быстроту вращательного движения характеризуют угловой скоростью. Ее обозначают буквой со (омега). При равномерном вращении угловая скорость равна отношению угла поворота 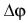 радиус-вектора к промежутку времени
радиус-вектора к промежутку времени 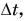 за который этот поворот произошел:
за который этот поворот произошел:

При равномерном вращении угловая скорость 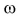 постоянна, а ее числовое значение равно углу поворота радиус-вектора за единицу времени.
постоянна, а ее числовое значение равно углу поворота радиус-вектора за единицу времени.
Единица угловой скорости в СИ — 1 радиан в секунду 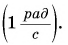
Как связан модуль линейной скорости 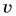 с угловой скоростью
с угловой скоростью 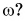 Подставив
Подставив 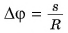 в формулу
в формулу 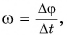 получим:
получим: 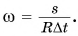 Отношение
Отношение 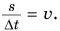 Значит, связь между угловой скоростью и модулем линейной скорости выражается формулой
Значит, связь между угловой скоростью и модулем линейной скорости выражается формулой

Равномерное вращение характеризуют также периодом обращения, который обозначается буквой Т. Он равен времени, за которое тело (материальная точка) совершает один полный оборот по окружности.
За промежуток времени 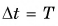 радиус-вектор поворачивается на угол
радиус-вектор поворачивается на угол 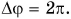 Значит, согласно формуле (2)
Значит, согласно формуле (2)

С периодом и угловой скоростью связана частота вращения. Ее обычно обозначают греческой буквой 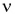 (ню).
(ню).
Частота вращения равна отношению числа оборотов N к промежутку времени 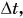 за которое они совершены:
за которое они совершены:

Из формулы (5) следует: частота вращения равна числу оборотов за единицу времени. Единицей частоты в СИ является 1 оборот в секунду, или 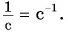
За промежуток времени, равный периоду 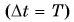 совершается один оборот: N = 1. Тогда согласно формуле (5)
совершается один оборот: N = 1. Тогда согласно формуле (5)

т. е. частота вращения 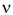 — величина, обратная периоду Т.
— величина, обратная периоду Т.
Из формул (4) и (6) следует связь между угловой скоростью и частотой вращения:

Угловая скорость пропорциональна частоте вращения.
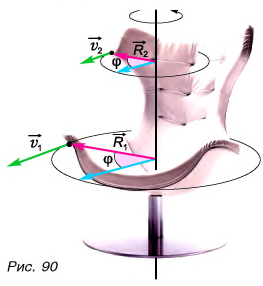
Мы рассмотрели движение материальной точки по окружности. Рассмотрим теперь равномерное вращение тела вокруг неподвижной оси (рис. 90).
Точки, находящиеся на оси, покоятся. Остальные точки тела описывают окружности, лежащие в плоскостях, перпендикулярных оси вращения. Углы поворота 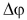 радиус-векторов этих точек за одно и то же время одинаковы. Значит, одинаковы период Т, частота
радиус-векторов этих точек за одно и то же время одинаковы. Значит, одинаковы период Т, частота 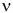 и угловая скорость
и угловая скорость 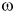 всех этих точек.
всех этих точек.
В то же время модули линейных скоростей точек тела различны. Они зависят от расстояния R точки до оси вращения (рис. 90). Согласно формуле (3)
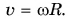
Модули линейных скоростей точек тела, равномерно вращающегося вокруг неподвижной оси, прямо пропорциональны расстоянию ДО этой оси.
Главные выводы:
- Угловая скорость вращательного движения численно равна углу поворота радиус-вектора за единицу времени.
- Единица угловой скорости — 1 радиан в секунду.
- Частота вращения есть величина, обратная периоду.
Пример решения задачи:
Вал электродвигателя кофемолки совершает N = 45 оборотов за время 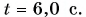 Определите период, частоту и угловую скорость равномерного вращения вала.
Определите период, частоту и угловую скорость равномерного вращения вала.
Решение Частота вращения вала:
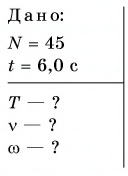
Решение
Частота вращения вала:
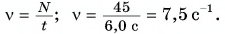
Учитывая связь между периодом и частотой, находим:
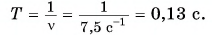
Угловая скорость:
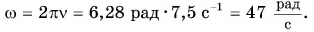
Ответ: 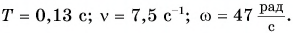
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |