Криволинейное движение материальной точки в теоретической механике

Содержание:

Криволинейное движение материальной точки:

В случае криволинейного движения по плоскости имеется два дифференциальных уравнения движения точки в декартовой системе координат, а в общем случае движения в пространстве— система трех дифференциальных уравнений. Дифференциальные уравнения криволинейного движения точки интегрируются сравнительно просто, если каждое из этих уравнений интегрируется независимо от других уравнений и при этом возможен один из трех рассмотренных случаев зависимости проекции равнодействующей силы от времени, координаты и скорости.

Рассмотрим примеры криволинейного движения точки в плоскости и в пространстве:

Пример 1. Материальная точка массой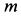

Определить уравнения движения точки и уравнение ее траектории в координатной форме.

Решение:

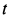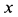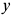Пусть в момент движущаяся точка имеет координаты и . Прикладываем к точке силу 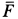и составляем дифференциальные уравнения ее движения в проекциях на оси координат. Имеем:

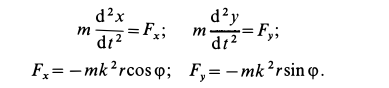
Учитывая, что

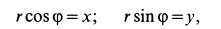
дифференциальные уравнения принимают форму

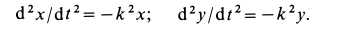
Для интегрирования этих уравнений можно применить подстановки

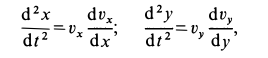
или интегрировать их как линейные дифференциальные уравнения с постоянными коэффициентами. Выполним интегрирование уравнений, используя подстановки. Имеем

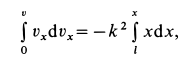
или

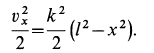
Аналогично для 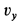получаем

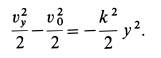
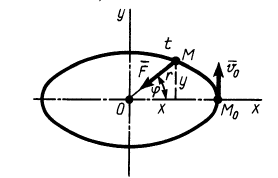
Рис. 11

Учитывая, что

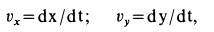
имеем

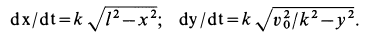
Эти дифференциальные уравнения интегрируем путем разделения переменных. Получаем

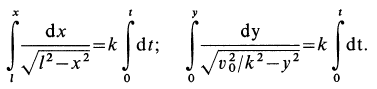
Выполняя интегрирование и подставляя пределы, имеем

или

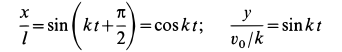
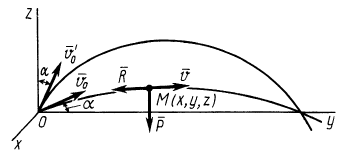
Рис. 12

и уравнения движения точки принимают вид

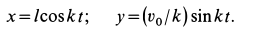
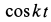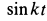Возводя в квадрат и , получаем уравнение траектории точки в координатной форме:

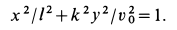
Траекторией точки оказался эллипс с полуосям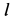и и .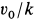

Пример 2. Материальная точка массой 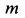 (рис. 12) брошена с поверхности Земли в вертикальной плоскости со скоростью 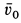под углом  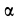к горизонту. Определить уравнения движения точки, если сила сопротивления воздуха, направленная против скорости, пропорциональна скорости и массе, т. 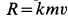е. , где 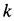— постоянный коэффициент пропорциональности.

Решение:

Задачу удобно решать в прямоугольной декартовой системе координат, начало которой находится в точке бросания, а ось 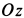направлена по вертикали вверх. Ос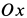и и 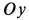 при этом расположатся в горизонтальной плоскости. Для определенности предположим, что начальная скорость 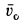располагается в плоскости 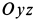. Для составления дифференциальных уравнений движения точки возьмем такое ее положение в момент 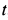, когда координаты точки 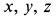и их первые производные по времени положительны. На точку действуют две силы: сила тяжести 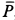, направленная по вертикали вниз, и сила сопротивления 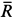, направление которой противоположно направлению скорости 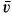. Равнодействующая сила

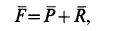
причем .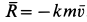

Для проекций равнодействующей силы 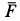на оси координат, считая, что в выбранном положении точки и положительных значениях 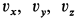, имеем

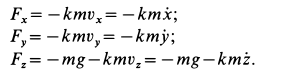
Знак минус у проекций силы сопротивления указывает на то, что их знаки противоположны знакам проекций скорости, принятым положительными.

Дифференциальные уравнения движения точки имеют вид

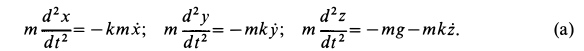
При сделанном выборе осей координат имеем следующие начальные условия:

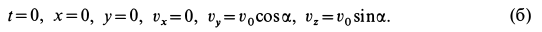
Каждое дифференциальное уравнение системы в рассматриваемом случае можно интегрировать отдельно, независимо от других уравнений. После сокращения на т дифференциальные уравнения примут вид

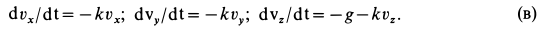
Разделяя переменные и интегрируя каждое из уравнений системы, получаем:

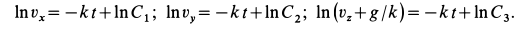
После потенцирования имеем:

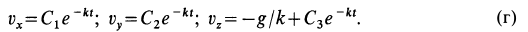
Подставляя в (г) начальные значения для 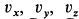, получаем уравнения для определения произвольных постоянных :

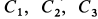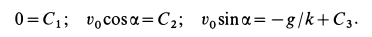
Постоянные интегрирования имеют следующие значения:

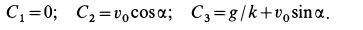
После подстановки постоянных интегрирования в (г) и замены проекций скорости на оси координат производными от координат по времени получаем

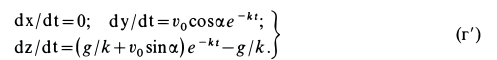
Разделяя в (г') переменные и интегрируя каждое дифференциальное уравнение первого порядка, имеем

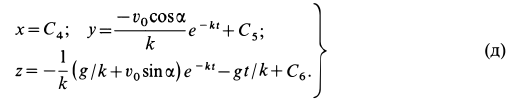
Подставляя в (д) начальные условия, получаем уравнения для определения постоянных интегрирования :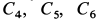

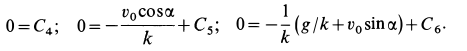
Отсюда находим

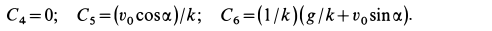
Подставляя значения постоянных в (д), получаем искомые уравнения движения точки:

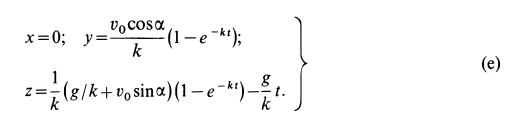
Проведем некоторые исследования движения точки. Из уравнений движения (е) путем предельного перехода при 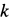, стремящемся к нулю, можно получить уравнения движения точки под действием только одной силы тяжести. Обозначая координаты точки в этом случае 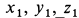, раскрываем неопределенности в уравнениях (е) по правилу Лопиталя. Для  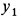 получаем

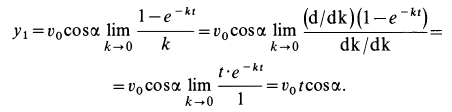
Прежде чем переходить к пределу в 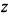, преобразуем его к виду

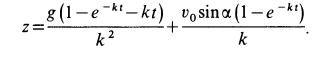
После этого

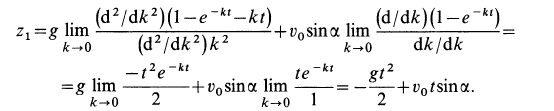
Получаем следующие уравнения движения точки под действием одной силы тяжести:

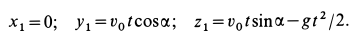
Если из этих уравнений исключить время 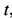,  то получим уравнения траектории точки в координатной форме (рис. 12):

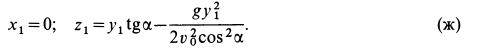
Траекторией точки является парабола, расположенная в плоскости .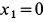

Если в (ж) принять 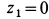, то 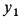при этом окажется горизонтальной дальностью 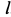, которая определяется по формуле

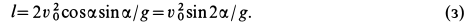
Из (з) следует, что наибольшая горизонтальная дальность получается при угле бросания :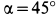

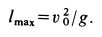
При других углах бросания 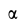одну и ту же дальность 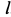, как это следует из (з), можно получить бросая точку под углом 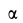к горизонту или под тем же углом 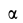к вертикали с той же самой скоростью .

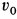Криволинейное движение точки

Как известно из кинематики, при движении материальной точки по криволинейной траектории ее ускорение 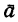имеет два составляющих ускорения: 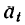— касательное (тангенциальное) и 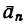— — нормальное (центростремительное).

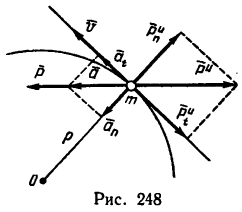
Из динамики уже известно, что ускорение 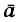, приобретенное точкой, есть результат действия определенной системы сил. Равнодействующая 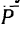этой системы и ускорение 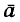(рис. 248) находятся в зависимости, выражающей основной закон динамики точки:

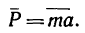
Если уравновесить силу 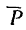приложением к точке силы инерции 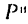, а затем разложить ее на две составляющие 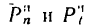соответственно по нормали и по касательной, то эти составляющие будут находиться в зависимости от нормальных и касательных ускорений, определяемых такими векторными равенствами:

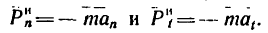
В задачах на криволинейное движение точки в основном рассматривается нормальная (центробежная) сила инерции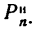

Числовое значение нормальной (центробежной) силы инерции можно выражать следующими формулами:

Заменим здесь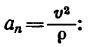

Если материальная точка, рассматриваемая в задаче, связана с каким-либо вращающимся телом, то скорость точки удобнее выражать через угловую скорость тела 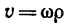и тогда

Если в последней формуле выразить массу точки через ее вес 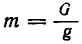, а угловую скорость — в об. мин 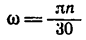то

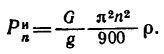
Здесь 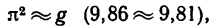поэтому формуле можно придать такой вид

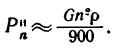(4)
Эта формула дает приближенное значение центробежной силы инерции, но она очень удобна при решении многих задач.

Последовательность решения задач на криволинейное движение точки при помощи метода кинетостатики та же, что в предыдущем параграфе.

Задача №1

Шарик, масса которого m= 0,5 кг, привязки к нити длиной 0,7 м. Нить вместе с шариком вращается в вертикальной плоскости, затрачивая на один оборот 1 сек. Определить натяжение шнура в моменты высшего и низшего положения шарика, считая, что скорость остается постоянной при перемещении по всей длине окружности.

Решение.

1.    В соответствии с условием задачи считаем, что шарик движется равномерно по окружности, радиус которой равен длине нити (r=0,7 м). Следовательно, его скорость

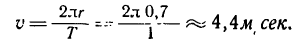
Оставаясь численно неизменной, скорость точки непрерывно изменяет направление, значит точка имеет нормальное ускорение

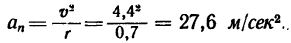
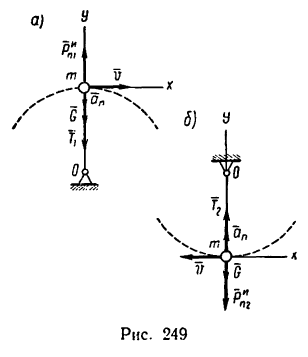
2.    Рассмотрим движущийся шарик в тот момент, когда он проходит через верхнюю точку траектории (рис. 249, а).

На шарик действуют две силы: его вес 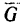и реакция нити 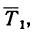равная ее натяжению. Заметим, что обе силы направлены в одну сторону — к точке О подвеса, так как вес всегда направлен вертикально вниз. Реакция гибкой связи всегда направлена вдоль нити от тела, которое удерживается нитью. Шарик, привязанный к нити и приведенный в движение, стремится согласно закону инерции двигаться равномерно и прямолинейно и поэтому он постоянно натягивает пить.

3.    Добавим к силам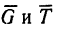 силу инерции 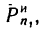направив ее в сторону, противоположную ускорению 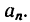Образовав таким образом уравновешенную систему сил, получим уравнение равновесия

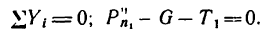
4.    Из уравнения разновесия находим 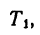учитывая, что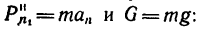

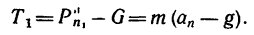
Подставим в это уравнение числовые значения:

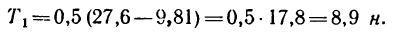
Таким образом, находясь в верхнем положении, двигающийся шарик натягивает пить силой 8,9 н, что соответствует0,91 кГ.

Отметим, что натяжение нити будет ослабевать при уменьшении скорости движения шарика. Следовательно, для того чтобы шарик при движении в вертикальной плоскости смог пройти верхнюю точку траектории с заданным радиусом кривизны р, он должен иметь в этой точке определенную скорость.

5.    Рассмотрим теперь движущийся шарик в момент прохождения нм нижней точки траектории (рис. 249,6).

В этом положении на шарик действуют также две силы: вес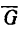 и реакция нити 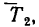но в отличие от предыдущего случая эти силы, действуя вдоль одной прямой, направлены в противоположные стороны.

6.    Добавим к силам 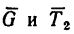силу инерции 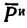и составим уравнение равновесия:

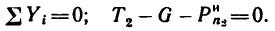
7.    Находим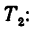

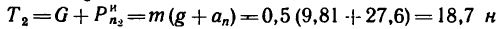
или приблизительно

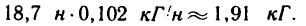
Как видно, при прохождении через нижнюю точку траектории шарик создает наибольшее натяжение нити.

Задача №2

Шарик А, масса которого 2 кг, подвешен на нити длиной 60 см, закрепленной в точке В. Он равномерно двигается по окружности в горизонтальной плоскости так, что нить описывает коническую поверхность и образует с вертикалью угол а = 30°. Определить натяжение нити и скорость шарика.

Решение 1 — с применением метода проекций.

1.    Если масса шарика m=2 кг, то его вес G = mg = 2* 9,81 =19,62 н.Кроме веса, на шарик действует натяжение (реакция 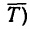нити. Длина нити l= 60 см = 0,6 м.

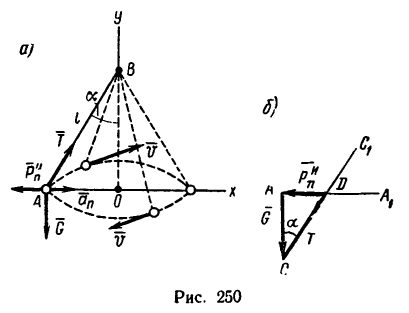
Изобразим двигающийся шарик с приложенными к нему силами G и 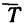(рис. 250,а). Так как шарик

мерно, то он имеет только

6.    Добавим к силам 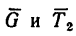силу инерции 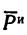и составим уравнение равновесия:

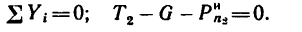
7.    Находим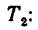

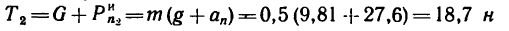
или приблизительно

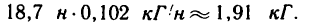
Как видно, при прохождении через нижнюю точку траектории шарик создает наибольшее натяжение нити.

• Заказать решение задач по теоретической механике

Задача №3

Шарик А, масса которого 2 кг, подвешен на нити длиной 60 см, закрепленной в точке В. Он равномерно двигается по окружности в горизонтальной плоскости так, что нить описывает коническую поверхность и образует с вертикалью угол а = 30°. Определить натяжение нити и скорость шарика.

Решение 1 — с применением метода проекций.

1.    Если масса шарика m=2 кг, то его вес G = mg = 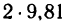=19,62 н

Кроме веса, на шарик действует натяжение (реакция 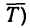нити. Длина нити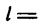

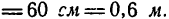
Изобразим двигающийся шарик с приложенными к нему силами 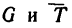(рис. 250,а). Так как шарик мерно, то он имеет только
движется по окружности равно-нормальное ускорение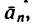, направленное по радиусу АО = r окружности. Применяя принцип Даламбера, для уравновешивания сил Т и G приложим к шарику нормальную (центробежную) силу инерции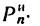

Изображая на рис. 250 силу инерции, необходимо учитывать, что она прикладывается к шарику условно. В действительности, сила инерции, как известно, приложена к двигающему телу или к связи. В данном случае нить служит для шарика и двигающим телом (через нить шарик приводится в движение), и связью (нить одновременно и ограничивает движение шарика). Поэтому сила инерции приложена к нити и отклоняет ее су вертикали.

2. Совместив оси координат с прямыми AO и ВО и спроектировав силы на оси х и у, выведем уравнения равновесия:

3. Из уравнения (2)

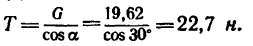
4 Из уравнения (1)

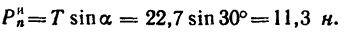
Так как

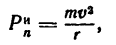
где 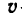—искомая скорость шарика, а радиус окружности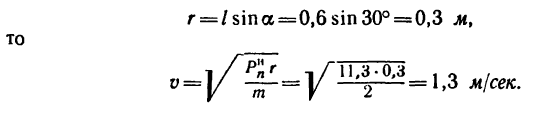
Таким образом, натяжение нити составляет 22,7 н при скорости движения шарика 1,3 м/сек.

Решение 2—с применением графо-аналитического метода.

1.    Этот вариант решения начинаем так же, как и предыдущий: изображаем шарик с действующими на него силами С = 19,62 н и искомой Т, а затем добавляем силу инерции 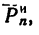направленную противоположно вектору 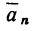(см. рис. 250, о).

2.    Силы 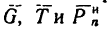образуют уравновешенную систему, поэтому многоугольник, построенный из векторов этих сил, должен быть замкнутым. Построение силового многоугольника начинаем с изображения вектора 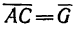(рис. 250,6). Затем из точек С и A проводим соответственно линии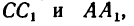параллельные направлениям сил 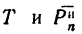(см. рис. 250,а). Прямые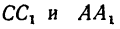пересекаются в точке D и образуется векторный прямоугольный треугольник 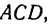в котором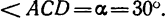

3.    Из прямоугольного треугольника ACD имеем:

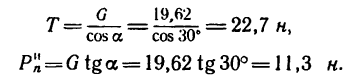
И, наконец, так же как и в первом решении, находим скорость движения шарика по окружности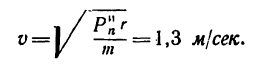

Задача №4

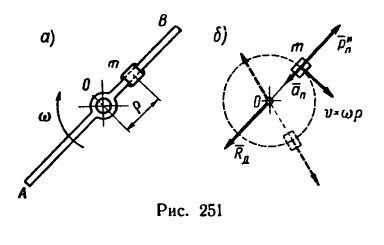
Тонкий стержень AВ, центр тяжести которого расположен на его оси О, вращается с угловой скоростью n -3009 об, мин.

На сколько увеличится нагрузка на подшипник, в котором вращается стержень, если на одну из половинок стержня прикрепить массу m — 0,5 кг, на расстоянии р = 0,1 м от оси вращения (рис. 251,а).

Решение.

1.    Стержень АВ без прикрепленной к нему массы т создает нагрузку на подшипник, равную его собственному весу. Причем, если стержень хорошо центрирован, т. е. его центр тяжести расположен точно на оси подшипника, то нагрузка при вращении не изменится — она также будет равна весу стержня и будет действовать на подшипник вертикально вниз.

2.    Если к стержню, по условию задачи, прикрепить массу m, то эта масса (примем ее за материальную точку), двигаясь по окружности радиусом р = 0,1 м, начнет растягивать ту часть стержня, которая расположена между массой т и подшипником, силой, равной 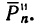Благодаря этому возникает дополнительная так называемая динамическая нагрузка на подшипник, уравновешиваемая его реакцией 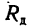(рис. 251,6).

3.    Так как увеличение нагрузки равно возникшей силе инерции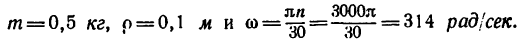
Подставим эти значения в формулу (3):

PJ| = 0,5 • 3142 • 0,1 =4929,8 н?«4,93 кн.
Таким образом, в результате прикрепления массы т нагрузка на подшипник увеличивается почти на 5 кн, что соответствует почти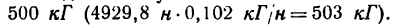

4. Применив формулу (4) и положив в ней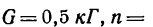 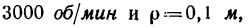м, найдем силу инерции 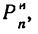выраженную в кГ:

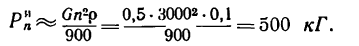
Результат, получившийся в этой задаче, подтверждает необходимость тщательной балансировки вращающихся деталей машин. Несбалансированные детали при вращении создают огромные дополнительные динамические нагрузки, которые приводят к быстрому износу подшипников.