Критерий совместности Кронекера-Капелли с примерами решения

Содержание:

Критерий совместности Кронекера-Капелли

Система линейных уравнений имеет вид: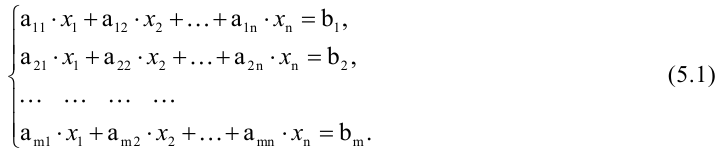

Здесь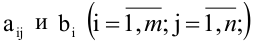

Используя понятие произведения матриц, можно переписать систему (5.1) в виде:

где 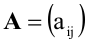- матрица, состоящая из коэффициентов при неизвестных системы (5.1), которая называется матрицей системы,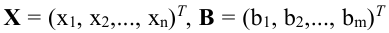векторы-столбцы, составленные соответственно из неизвестных 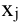и из свободных членов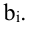

Упорядоченная совокупность n вещественных чисел 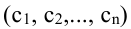называется решением системы (5.1), если в результате подстановки этих чисел вместо соответствующих переменных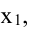 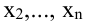каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор 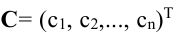такой, что АС = В.

Система (5.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

Матрица 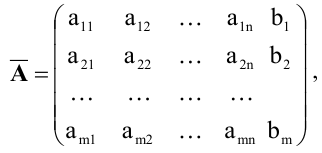образованная путем приписывания справа к матрице А столбца свободных членов, называется расширенной матрицей системы.

Вопрос о совместности системы (5.1) решается следующей теоремой.

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц 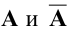совпадают, т.е.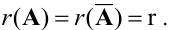

Для множества М решений системы (5.1) имеются три возможности:

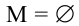1. (в этом случае система несовместна);
2. М состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной)',
3. М состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.

Система имеет единственное решение только в том случае, когда 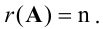При этом число уравнений - не меньше числа неизвестных 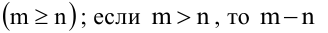уравнений являются следствиями остальных.

Если 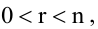то система является неопределенной.

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа: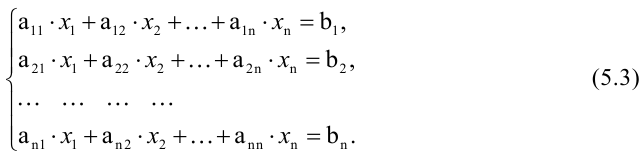

Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера; 3) матричным методом.

• Заказать решение задач по высшей математике

Пример:

Исследовать систему уравнений и решить ее, если она совместна:

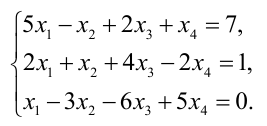
Решение:

Выписываем расширенную матрицу системы: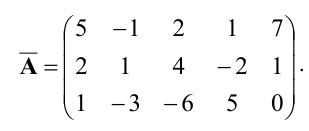

Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 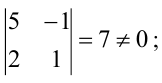содержащие его миноры третьего порядка равны нулю: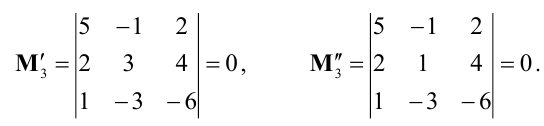

Следовательно, ранг основной матрицы системы равен 2, т.е. 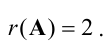Для вычисления ранга расширенной матрицы 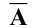рассмотрим окаймляющий минор 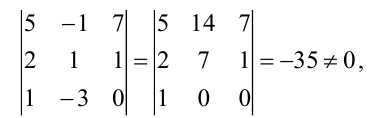значит, ранг расширенной матрицы 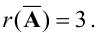Поскольку 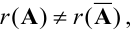то система несовместна.