
Кратный интеграл - определение с примерами решения
Содержание:
В теории определенного интеграла для нахождения площади криволинейной трапеции вводится понятие интегральной суммы, пределом которой является определенный интеграл. Определенный интеграл существует для трех типов функций: непрерывных, кусочно-непрерывных и монотонных. Задача интегрирования может быть также сформулирована и для функции n переменных, заданной в ограниченной области 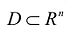
Интегрирование функций многих переменных
Понятие двумерной интегральной суммы, пределом которой является двойной интеграл, можно ввести на основе задачи об объеме тела.
Задача: Найти объем тела, ограниченного сверху непрерывной поверхностью 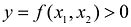
Для этого разобьем основание S на конечное число элементарных ячеек 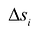 и в каждой из этих ячеек выберем точку
и в каждой из этих ячеек выберем точку 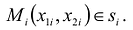 Объем такого элемента равен
Объем такого элемента равен 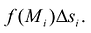 Объем всей фигуры можно приближенно найти как сумму
Объем всей фигуры можно приближенно найти как сумму 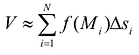 с любой степенью точности в зависимости от числа ячеек
с любой степенью точности в зависимости от числа ячеек 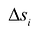 и, соответственно, их размера. Если предположить, что число элементарных ячеек
и, соответственно, их размера. Если предположить, что число элементарных ячеек 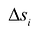 бесконечно возрастает, а их диаметр при этом является величиной бесконечно малой, то можно получить точное выражение для объема всей фигуры:
бесконечно возрастает, а их диаметр при этом является величиной бесконечно малой, то можно получить точное выражение для объема всей фигуры: 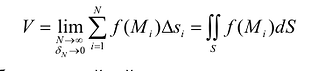
Таким образом, двойной интеграл имеет простой геометрический смысл, он выражает объем криволинейного цилиндрического бруса, ограниченного сверху непрерывной поверхностью 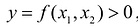 , снизу - конечной замкнутой областью S плоскости
, снизу - конечной замкнутой областью S плоскости 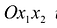 и с боков - прямой цилиндрической поверхностью, построенной на границе объекта S и имеющей образующие, перпендикулярные плоскости
и с боков - прямой цилиндрической поверхностью, построенной на границе объекта S и имеющей образующие, перпендикулярные плоскости 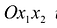 .
.
Двумерной интегральной суммой от данной функции 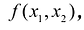 определенной на области S называется сумма парных произведений площадей элементарных ячеек
определенной на области S называется сумма парных произведений площадей элементарных ячеек 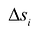 области S на значения функции
области S на значения функции 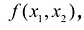 в точке
в точке 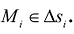
Двойным интегралом от функции 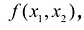 определенной на области S называется предел соответствующей двумерной интегральной суммы при неограниченном возрастании числа N элементарных ячеек
определенной на области S называется предел соответствующей двумерной интегральной суммы при неограниченном возрастании числа N элементарных ячеек 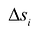 и стремлении к нулю их наибольшего диаметра
и стремлении к нулю их наибольшего диаметра 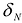 при условии, что этот предел существует и не зависит от способа разбиения области S на элементарные ячейки
при условии, что этот предел существует и не зависит от способа разбиения области S на элементарные ячейки 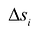 и выбора точек
и выбора точек 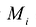 в них.
в них.
Теорема. Если область S с кусочно-непрерывной границей I ограничена и замкнута, а функция 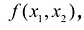 непрерывна в области S, то двойной интеграл
непрерывна в области S, то двойной интеграл
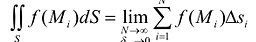 , т.е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа разбиения области S на элементарные ячейки
, т.е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа разбиения области S на элементарные ячейки 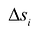 и выбора точек
и выбора точек 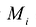 в них.
в них.
Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем целесообразно пользоваться наиболее удобным для декартовой системы координат разбиением на прямоугольную сетку, образованную пересечением двух систем прямых, параллельных соответственно координатным осям Ох и Оу. В этом случае элементарными ячейками являются прямоугольники, со сторонами 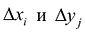 . Таким образом, в обозначении интеграла можно учесть что
. Таким образом, в обозначении интеграла можно учесть что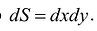 Тогда:
Тогда: 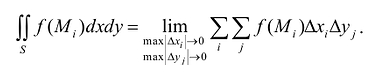
Для вычисления двойного интеграла применяется процедура повторного интегрирования.
Предположим для определенности, что область интегрирования S представляет собой криволинейную трапецию: 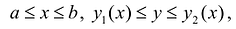 где
где 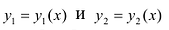 - однозначные непрерывные функции на отрезке [а,b]. Важно отметить, что вертикаль, проходящая через любую точку х па отрезке [а,b) оси Ох, пересекает границу области интегрирования S только в двух точках: в точке входа
- однозначные непрерывные функции на отрезке [а,b]. Важно отметить, что вертикаль, проходящая через любую точку х па отрезке [а,b) оси Ох, пересекает границу области интегрирования S только в двух точках: в точке входа 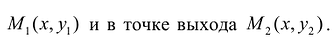 Такая область называется стандартной относительно оси Оу.
Такая область называется стандартной относительно оси Оу.
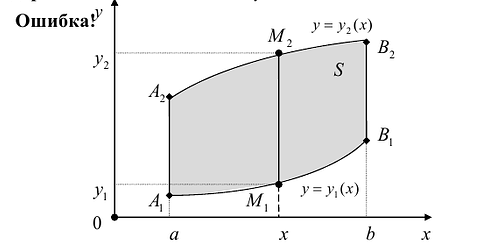
Теорема. Если для функции f(x,y) определенной в области S (стандартной относительно оси Оу), существует двойной интеграл 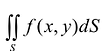 и существует интеграл
и существует интеграл 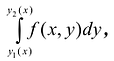 то
то 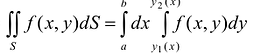 .
.
При этом, интеграл 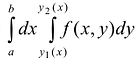 называется повторным.
называется повторным.
Таким образом, вычисление двойного интеграла сводится к вычислению двух интегралов: вначале находится внутренний интеграл по переменной у (при этом переменная х рассматривается как постоянная величина); после этого полученное выражение повторно интегрируется по переменной х.
Задача вычисления кратного интеграла может быть обобщена на n-мерный случай и аналогично решена путем сведения кратного интеграла к повторному. Пусть функция у = f(M) определена и ограничена в замкнутой области 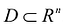 . Область D разбивается на N элементарных частей
. Область D разбивается на N элементарных частей 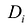
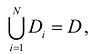 пересечением любой пары элементарных частей будет множество точек, размерность которого не превышает n -1.
пересечением любой пары элементарных частей будет множество точек, размерность которого не превышает n -1.
В каждой элементарной части выбирается точка 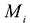 и составляется интегральная сумма:
и составляется интегральная сумма: 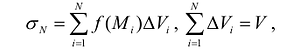 где
где 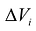 - объемная мера области
- объемная мера области 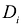 ; V-объемная мера области D.
; V-объемная мера области D.
Для того чтобы вычислить интегральную сумму, необходимо, чтобы элементарные части 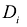 допускали исчисление объемной меры в достаточно простой и редуктируемой форме.
допускали исчисление объемной меры в достаточно простой и редуктируемой форме.
n-кратным интегралом функции у = f(M) по области D называется предел интегральной суммы 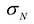 при
при 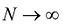 и, соответственно,
и, соответственно, 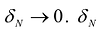 - наибольшая протяженность элементарной области
- наибольшая протяженность элементарной области 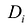 для данного разбиения.
для данного разбиения.
Этот предел не должен зависеть от способов разбиения D на части и от выбора точек 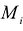 в каждой из них. Указанный интеграл можно представить в следующим образом:
в каждой из них. Указанный интеграл можно представить в следующим образом:
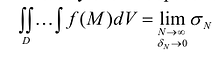
По форме этот интеграл сходен с определенным интегралом 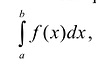 , который также является пределом интегральной суммы:
, который также является пределом интегральной суммы:
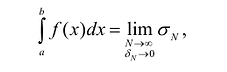
где 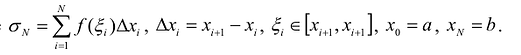
Очевидно, что в n-кратном интеграле, как и в случае определенного интеграла, интегральные суммы ограничены снизу и сверху значениями сумм Дарбу 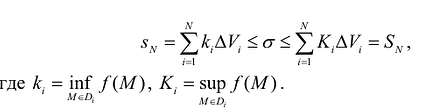
Свойствами одномерных сумм Дарбу обладают и n -мерные суммы. При этом для любой ограниченной функции: 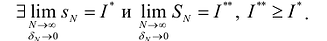
Необходимым и достаточным условием интегрируемости функции является условие 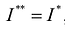 , что эквивалентно выражению:
, что эквивалентно выражению:
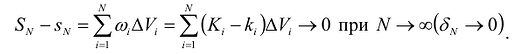
Величина 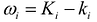 , называется колебанием функции в элементарной области
, называется колебанием функции в элементарной области 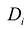 и является величиной положительной при любом i.
и является величиной положительной при любом i.
В результате можно установить, что к числу интегрируемых функций будут относиться функции, непрерывные на замкнутой области D. При вычислении n-кратный интеграл сводится к повторному интегралу, т.е. вычислению обычного интеграла от внутреннего интеграла кратности n -1.
Свойства n-кратного интеграла
- Интеграл по области, имеющей нулевую «объемную» меру в
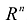 , равен нулю. При этом к областям с нулевой «объемной» мерой в
, равен нулю. При этом к областям с нулевой «объемной» мерой в 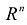 , относятся разнообразные множества, которые заданы в пространстве
, относятся разнообразные множества, которые заданы в пространстве 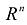 , (m
, (m- Если две функции f(M) и g(M) интегрируемы в D, то сумма этих функций также интегрируема в D и
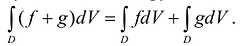
- Если функция f(M) интегрируема в D, а С - постоянная величина, то функция С f(M) также интегрируема в D и
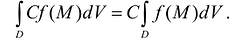
- Пусть область D является объединением областей
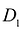 и
и 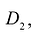 , а пересечение этих областей есть множество S, размерность которого меньше N. Если функция f(M) интегрируема в D, то она интегрируема в
, а пересечение этих областей есть множество S, размерность которого меньше N. Если функция f(M) интегрируема в D, то она интегрируема в 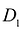 и
и 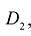 и при этом
и при этом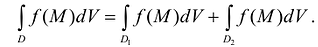
- Если функция f(M) определена и интегрируема в D, и при этом
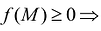 (за исключением, быть может, некоторой части D с размерностью меньше n), то
(за исключением, быть может, некоторой части D с размерностью меньше n), то 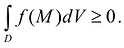
- Если две функции /fМ) и g(M) определены и интегрируемы в D, причем
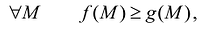 то
то 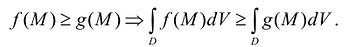
- Если функция f(M) определена и интегрируема в D, то
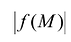 также интегрируема в D, причем
также интегрируема в D, причем 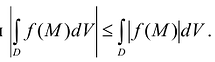
- Если функция f(M) = С является постоянной
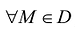 , то
, то 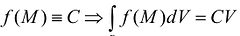 .
.- Если функция f(M) определена и интегрируема в D и ограничена снизу и сверху значениями к к К, соответственно
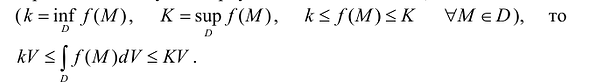
- Если две функции f(M) и g(M) интегрируемы в D, то сумма этих функций также интегрируема в D и
Понятие о двойном интеграле
Мы рассматривали определенный интеграл, как предел суммы для случая, когда функция f(x) определена на отрезке 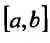 , который называется отрезком интегрирования. В настоящем параграфе мы обобщим понятие интеграла на случай, когда областью интегрирования является некоторая область на плоскости, или некоторая область в пространстве, при этом мы будем пользоваться интуитивным представлением площади и объема.
, который называется отрезком интегрирования. В настоящем параграфе мы обобщим понятие интеграла на случай, когда областью интегрирования является некоторая область на плоскости, или некоторая область в пространстве, при этом мы будем пользоваться интуитивным представлением площади и объема.
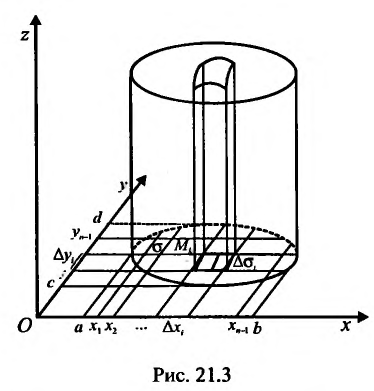
Пусть 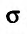 - ограниченная плоская область (см. рис. 21.3). Рассмотрим функцию z = f{x,y), определенную и непрерывную в области
- ограниченная плоская область (см. рис. 21.3). Рассмотрим функцию z = f{x,y), определенную и непрерывную в области 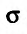 , ограниченной замкнутой линией L. Разобьем область о на элементарные области
, ограниченной замкнутой линией L. Разобьем область о на элементарные области 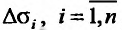 , произвольной формы, при-чем через
, произвольной формы, при-чем через 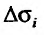 , обозначим сами элементарные области и их площади. В каждой из элементарных областей
, обозначим сами элементарные области и их площади. В каждой из элементарных областей 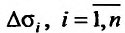 произвольно выберем точки
произвольно выберем точки 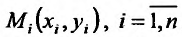 , и вычислим значения функции в этих точках:
, и вычислим значения функции в этих точках: 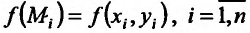 . Составим сумму произведений значений функции
. Составим сумму произведений значений функции 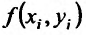 на площади
на площади 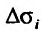 :
:
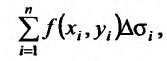 которая называется интегральной суммой.
которая называется интегральной суммой.
Предел этой интегральной суммы при неограниченном увеличении числа делений и неограниченном уменьшении каждой из элементарных областей 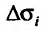 , если он существует, называется двукратным (двойным) интегралом от функции f(x,y) и обозначается
, если он существует, называется двукратным (двойным) интегралом от функции f(x,y) и обозначается 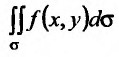
Если 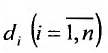 - максимальное расстояние между двумя точками элементарной области
- максимальное расстояние между двумя точками элементарной области 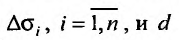 - наибольшее из этих чисел:
- наибольшее из этих чисел: 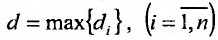 то неограниченное уменьшение каждой из элементарных областей равносильно тому, что
то неограниченное уменьшение каждой из элементарных областей равносильно тому, что 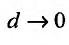 . Тогда можно записать:
. Тогда можно записать:
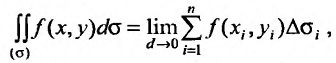
где f(х,у) - подынтегральная функция, а 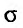 - область интегрирования.
- область интегрирования.
Если отнести область 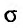 к прямоугольной системе координат (см. рис. 21.3), то
к прямоугольной системе координат (см. рис. 21.3), то 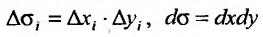 (элемент площади) и тогда справедливо равенство:
(элемент площади) и тогда справедливо равенство:
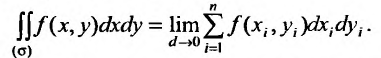
Геометрический смысл двойного интеграла состоит в том, что он равен объему цилиндра с основанием о и ограниченного сверху поверхностью 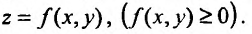
Вычисление двойного интеграла сводится к вычислению двух определенных интегралов; при вычислении "внутреннего интеграла" (записанного в скобках) х (у) считается постоянным (рис. 21.4):
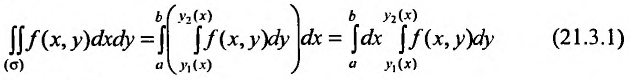
или (рис. 21.5)
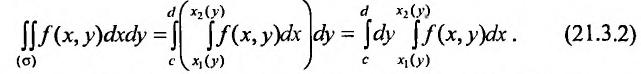
Если область интегрирования о отлична от областей, указанных на рисунках 21.4 и 21.5, то ее разбиваем на части прямыми, параллельными оси Ох и оси Оу, чтобы каждая из полученных частей имела соответствующий вид. 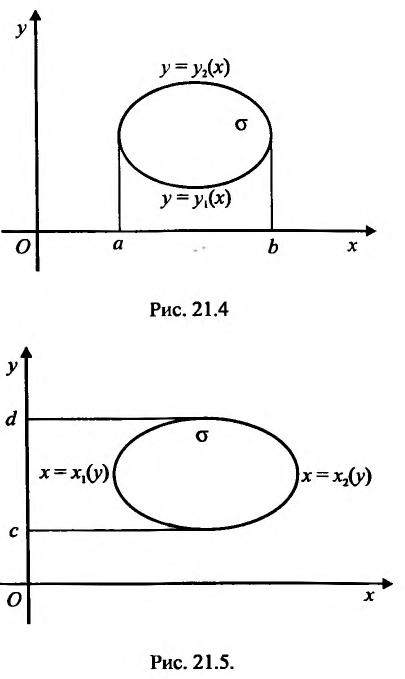
Пример №1
Вычислить двойной интеграл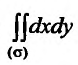 по области
по области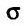 , ограниченной линиями:
, ограниченной линиями: 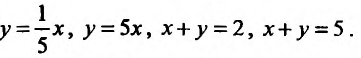
Решение:
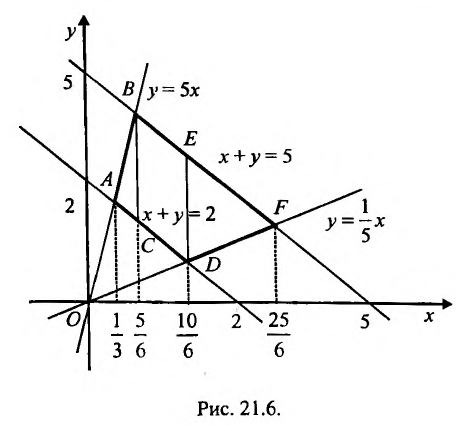
Построим на плоскости хОу область а (см. рис. 21.6).
Из рисунка 21.6 мы видим, что область  отлична от областей, указанных на рисунках 21.5 и 21.6, так как ни одну из границ в направлении оси Ох или оси Оу нельзя записать одним уравнением
отлична от областей, указанных на рисунках 21.5 и 21.6, так как ни одну из границ в направлении оси Ох или оси Оу нельзя записать одним уравнением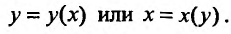
Поэтому разобьем заданную область на части прямыми 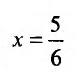
(абсцисса точки пересечения прямых _у = 5х и х + у = 5) и 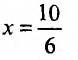
(абсцисса точки пересечения прямых 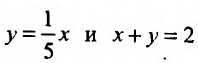 ). Тогда заданный интеграл будет равен сумме трех интегралов по областям: ABC, CBED, DEF:
). Тогда заданный интеграл будет равен сумме трех интегралов по областям: ABC, CBED, DEF: 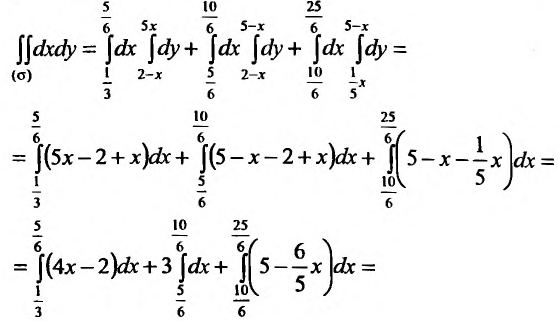
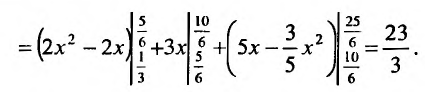
Понятие о тройном интеграле
По аналогии с двойным интегралом вводится понятие тройного интеграла. Пусть задана замкнутая пространственная область V, в которой задана непрерывная функция 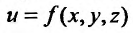 . Разобьем область V на и элементарных пространственных областей
. Разобьем область V на и элементарных пространственных областей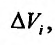
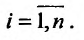 . Составим сумму произведений значений функции на объемы элементарных областей:
. Составим сумму произведений значений функции на объемы элементарных областей:
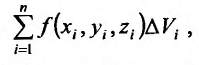
которая называется интегральной суммой.
Обозначим 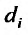 - максимальное расстояние между двумя точками элементарной пространственной области
- максимальное расстояние между двумя точками элементарной пространственной области 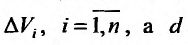 -наибольшее из этих чисел:
-наибольшее из этих чисел: 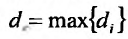 . Предел этой интегральной суммы, при неограниченном увеличении числа делений n и неограниченном уменьшении (при
. Предел этой интегральной суммы, при неограниченном увеличении числа делений n и неограниченном уменьшении (при 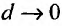 ) каждой из элементарных областей
) каждой из элементарных областей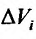 , если он существует, называется трехкратным (тройным) интегралом от функции f (х, у, z) и обозначается
, если он существует, называется трехкратным (тройным) интегралом от функции f (х, у, z) и обозначается
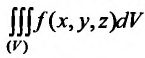 . Итак, по определению:
. Итак, по определению:
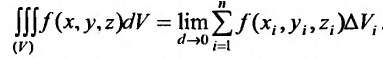
Если ввести в пространстве прямоугольные координаты, то будет справедливо равенство:
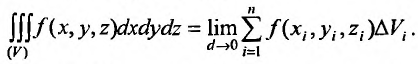
При вычислении тройного интеграла, он сводится к двойному интегралу, путем проектирования поверхности, ограничивающий объем V , на плоскость хОу в виде области 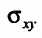 и определение координат
и определение координат 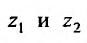 точек входа и выхода прямой, параллельной оси Oz и проведенной через точку (х, у) области
точек входа и выхода прямой, параллельной оси Oz и проведенной через точку (х, у) области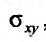 и вычисления интеграла
и вычисления интеграла 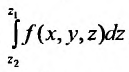 , считая х и у постоянными, а затем вычисляется двойной интеграл:
, считая х и у постоянными, а затем вычисляется двойной интеграл:
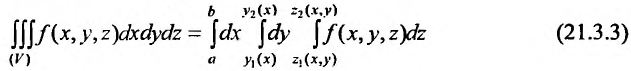
или
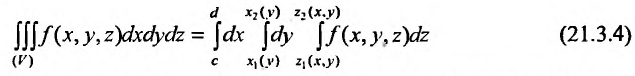
Кратные интегралы (двойные и тройные) удовлетворяют следующим основным свойствам:
- Постоянный множитель можно выносить за знак кратного интеграла.
- Кратный интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме кратных интегралов от отдельных слагаемых.
- Если подынтегральная функция интегрируема в области, а эта область разбита на две непересекающиеся части, то кратный интеграл по области равен сумме кратных интегралов по непересекающимся частям.
Пример №2
Вычислить тройной интеграл 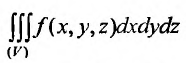 по пространственной области V, ограниченной плоскостями:
по пространственной области V, ограниченной плоскостями: 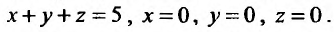
Решение:
Область V является треугольной пирамидой (см. рис. 21.7), ограниченной плоскостью х + у + z = 5 . Спроектируем поверхность, ограничивающую объем V, на плоскость хОу, получим греугольник ЛОВ, при этом z будет изменяться от 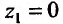 до
до 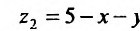 . Двойной интеграл
. Двойной интеграл 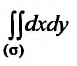 вычислим, используя формулу (21.3.1).
вычислим, используя формулу (21.3.1). 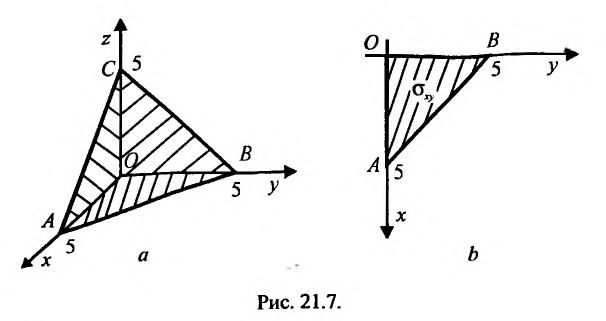
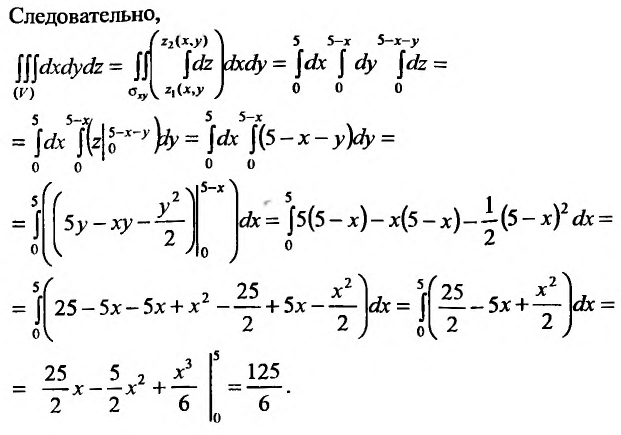
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |