
Ковариация в теории вероятности - определение и вычисление с примерами решения
Содержание:
Ковариация:
Важную информацию о системе случайных величин 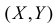
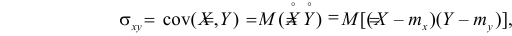
которая называется ковариацией или ковариационным моментом. Заметим, что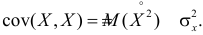 Из определения ковариации следует, что
Из определения ковариации следует, что 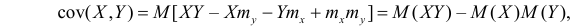
откуда
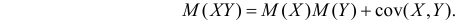
Кроме того, 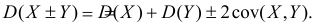
Если случайные величины X и Y независимы, то их ковариация равна нулю и тогда

Ковариация содержит информацию о зависимости между величинами. Но значение 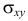 изменяется при изменении единиц измерения X и Y. Поэтому для характеристики зависимости между величинами удобно рассматривать величину
изменяется при изменении единиц измерения X и Y. Поэтому для характеристики зависимости между величинами удобно рассматривать величину
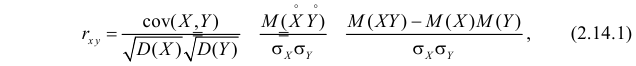
которая называется коэффициентом корреляции величин X и Y.
Величины 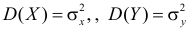 и
и 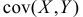 характеризуют разброс положений случайной точка на плоскости. Эти числовые характеристики принято записывать в виде матрицы
характеризуют разброс положений случайной точка на плоскости. Эти числовые характеристики принято записывать в виде матрицы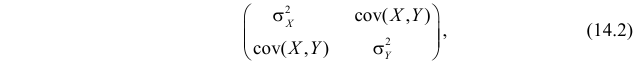
которую называют ковариационной матрицей системы случайных величин (X,Y).
Корреляционная зависимость
Наиболее простой и известной формой зависимости между величинами является функциональная зависимость, при которой каждому значению аргумента соответствует строго определенное значение функции. Функциональная зависимость может быть и между случайными величинами. Существует иной, широко распространенный в природе, тип зависимости между случайными величинами. Эта зависимость проявляется в том, что закон распределения одной случайной величины изменяется при изменении другой. Такая зависимость называется статистической.
Следует заметить, что функциональная зависимость бывает лишь в теоретических построениях или в условиях специально подготовленных опытов. Физический опыт в том и состоит, что исследователь старается по возможности исключить влияние всех посторонних факторов и наблюдать зависимость в чистом виде.
Явления окружающего нас мира взаимосвязаны и воздействие одной переменной на другую происходит при одновременном воздействии множества других переменных, поэтому даже функциональные зависимости проявляются как зависимости статистические.
Итак, при статистической зависимости изменение одной величины приводит к изменению закона распределения другой. Если Y – дискретная случайная величина, то это означает, что при каждом фиксированном значении 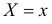 имеется набор возможных значений
имеется набор возможных значений 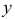 и соответствующих им вероятностей
и соответствующих им вероятностей 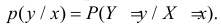 Последним обозначением подчеркивается, что речь идет о событии
Последним обозначением подчеркивается, что речь идет о событии 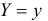 при условии, что произошло событие
при условии, что произошло событие 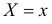 .
.
Набор возможных значений 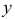 и соответствующих им условных вероятностей образует условный закон распределения
и соответствующих им условных вероятностей образует условный закон распределения 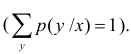
Для непрерывной случайной величины можно ввести понятие условной функции распределения или условной плотности вероятности. Если рассмотреть вероятности событий 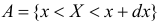 и
и 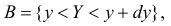 то по аналогии с теоремой умножения вероятностей событий можно получить для условной плотности вероятности
то по аналогии с теоремой умножения вероятностей событий можно получить для условной плотности вероятности 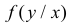 соотношение
соотношение 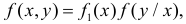 где
где 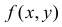 – плотность вероятности системы
– плотность вероятности системы 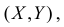 а
а 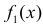 – маргинальная плотность вероятности случайной величины X. Из этого соотношения
– маргинальная плотность вероятности случайной величины X. Из этого соотношения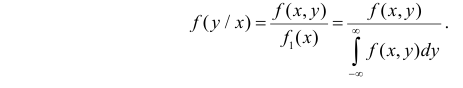
На протяжении этого раздела будем проводить выкладки только для дискретных случайных величин. Для непрерывных случайных величин все рассуждения и выводы останутся в силе, если заменить суммы на интегралы, а вероятности на плотности вероятности.
Статистическая зависимость сложна для изучения. Трудно проследить за изменением всего закона распределения сразу. Проще сосредоточиться на изучении изменения числовых характеристик, в первую очередь математического ожидания. Условный закон распределения имеет числовые характеристики такие же, как и обычные законы распределения. В частности, 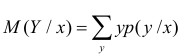 – для дискретной случайной величины называют условным математическим ожиданием, или средним значением Y при заданном значении
– для дискретной случайной величины называют условным математическим ожиданием, или средним значением Y при заданном значении 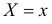 . Для непрерывной случайной величины его вычисляют в виде
. Для непрерывной случайной величины его вычисляют в виде 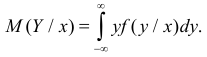 Если условные математические ожидания при разных значениях X соединить, то получится линия, называемая линией регрессии Y на X. Уравнение этой линии называют уравнением регрессии Y на X (см. рис. 2.14.1, на котором точками показаны возможные значения двумерной случайной величины
Если условные математические ожидания при разных значениях X соединить, то получится линия, называемая линией регрессии Y на X. Уравнение этой линии называют уравнением регрессии Y на X (см. рис. 2.14.1, на котором точками показаны возможные значения двумерной случайной величины 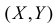 ).
).
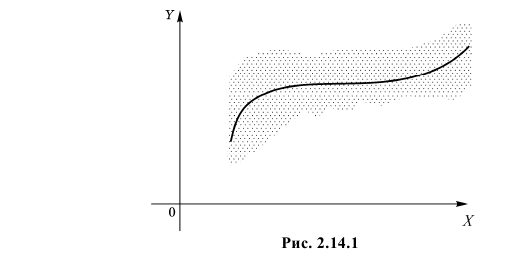
Корреляционной зависимостью Y от X называется функциональная зависимость условного среднего значения Y от X. Графиком корреляционной зависимости служит линия регрессии. Например, рост человека X и его вес Y связаны статистической зависимостью. Для каждого значения роста существует целое распределение возможных значений веса. Между этими величинами существует и корреляционная зависимость, которая для людей зрелого возраста выражается известной формулой:

Вместе с изменением условного среднего значения может изменяться и разброс Y относительно условного среднего значения. При каждом 142 значении 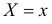 можно вычислить дисперсию соответствующих значений Y. Эту дисперсию называют условной дисперсией. Например, для дискретной случайной величины условная дисперсия равна
можно вычислить дисперсию соответствующих значений Y. Эту дисперсию называют условной дисперсией. Например, для дискретной случайной величины условная дисперсия равна 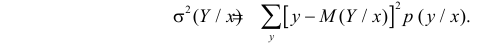
Всякую зависимость изучают для того, чтобы уметь по известному значению одной величины предсказывать значение другой. При статистической зависимости между величинами можно использовать для прогноза линию регрессии. Если стало известно, что 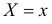 , то в качестве предполагаемого значения Y можно назвать соответствующее условное среднее значение
, то в качестве предполагаемого значения Y можно назвать соответствующее условное среднее значение 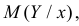 т.е. ординату линии регрессии при данном
т.е. ординату линии регрессии при данном 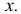 Если Y принимает значение
Если Y принимает значение 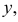 то
то 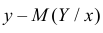 будет ошибкой прогноза и величину
будет ошибкой прогноза и величину 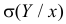 можно рассматривать как среднюю квадратическую ошибку прогноза Y по значению X при указанном способе действий.
можно рассматривать как среднюю квадратическую ошибку прогноза Y по значению X при указанном способе действий.
Представление о среднем квадрате ошибки прогноза Y по линии регрессии дает средняя из условных дисперсий
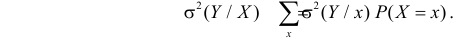
Здесь значения 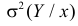 взяты с учетом вероятности каждого значения
взяты с учетом вероятности каждого значения 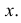 Величина
Величина 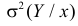 равна среднему квадрату отклонения значений Y от линии регрессии. Ее можно записать в виде
равна среднему квадрату отклонения значений Y от линии регрессии. Ее можно записать в виде 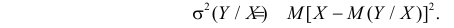
Заметим, что при прогнозе Y по любой другой линии средний квадрат ошибки прогноза будет больше. В самом деле, для любой постоянной 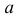
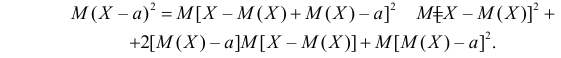
Второе слагаемое в правой части равно нулю, так как 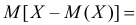
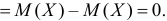 Третье слагаемое, очевидно, неотрицательно. Поэтому
Третье слагаемое, очевидно, неотрицательно. Поэтому 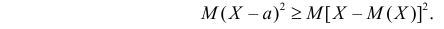
Равенство возможно лишь при 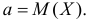 Это означает, что средняя квадратическая ошибка прогноза будет наименьшей, если случайную величину прогнозировать по ее среднему значению. Линия регрессии проходит через условные средние значения Y. Поэтому можно утверждать, что линия регрессии минимизирует среднюю квадратическую ошибку прогноза случайной величины Y по наблюдаемому значению величины X.
Это означает, что средняя квадратическая ошибка прогноза будет наименьшей, если случайную величину прогнозировать по ее среднему значению. Линия регрессии проходит через условные средние значения Y. Поэтому можно утверждать, что линия регрессии минимизирует среднюю квадратическую ошибку прогноза случайной величины Y по наблюдаемому значению величины X.
Линейная корреляция
Корреляция называется линейной, если линия регрессии одной величины на другую является прямой. В противном случае говорят о нелинейной корреляции.
Пусть линия регрессии имеет вид 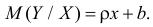 Согласно свойству линии регрессии, должен быть минимален средний квадрат отклонений Y от этой линии, т.е. минимальной должна быть величина
Согласно свойству линии регрессии, должен быть минимален средний квадрат отклонений Y от этой линии, т.е. минимальной должна быть величина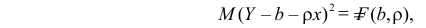
причем ее минимальное значение равно 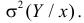
Параметры 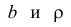 можно найти из условия минимума функции
можно найти из условия минимума функции 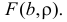 Необходимые условия экстремума дают систему уравнений
Необходимые условия экстремума дают систему уравнений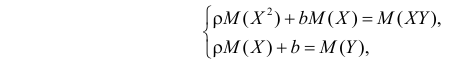
решения которой имеют вид 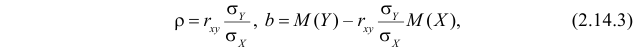
где 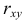 – коэффициент корреляции (2.14.1). Если выражения (2.14.3) подставить в
– коэффициент корреляции (2.14.1). Если выражения (2.14.3) подставить в 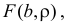 то после ряда преобразований получается, что
то после ряда преобразований получается, что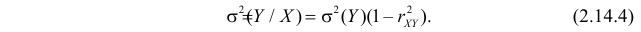
Из соотношений (2.14.3) и (2.14.4) можно извлечь информацию о свойствах коэффициента корреляции.
1. Так как 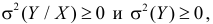 то
то 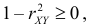 откуда
откуда 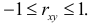
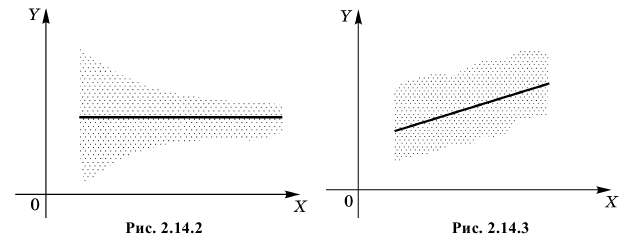
2. Если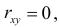 то в силу (2.14.3) и угловой коэффициент линии регрессии равен нулю. Линия регрессии параллельна оси ОX. В этом случае говорят, что величины некоррелированы, так как среднее значение Y не изменяется при изменении X. Отсутствие корреляционной зависимости не всегда означает независимость величин. Например, при постоянном среднем значении Y может изменяться разброс значений относительно среднего (см. рис. 2.14.2, на котором точками изображены возможные положения случайной точки).
то в силу (2.14.3) и угловой коэффициент линии регрессии равен нулю. Линия регрессии параллельна оси ОX. В этом случае говорят, что величины некоррелированы, так как среднее значение Y не изменяется при изменении X. Отсутствие корреляционной зависимости не всегда означает независимость величин. Например, при постоянном среднем значении Y может изменяться разброс значений относительно среднего (см. рис. 2.14.2, на котором точками изображены возможные положения случайной точки).
3. Из (2.14.3) следует, что угловой коэффициент линии регрессии 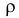 и коэффициент корреляции имеют одинаковые знаки. Если
и коэффициент корреляции имеют одинаковые знаки. Если 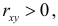 то говорят, что величины коррелированы положительно. В этом случае большему значению величины X соответствует большее среднее значение Y (см. рис. 2.14.3). Еще раз подчеркнем, что речь идет именно об увеличении среднего значения Y. В отдельных опытах большему X может соответствовать меньшее Y. Например, положительно коррелированы рост и вес человека, возраст и высота дерева, качество сырья и качество продукции и т.д.
то говорят, что величины коррелированы положительно. В этом случае большему значению величины X соответствует большее среднее значение Y (см. рис. 2.14.3). Еще раз подчеркнем, что речь идет именно об увеличении среднего значения Y. В отдельных опытах большему X может соответствовать меньшее Y. Например, положительно коррелированы рост и вес человека, возраст и высота дерева, качество сырья и качество продукции и т.д.
Если 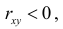 то говорят, что величины коррелированы отрицательно. Это означает, что большему значению одной величины соответствует в среднем меньшее значение другой. Например, число пропусков занятий и успеваемость коррелированы отрицательно.
то говорят, что величины коррелированы отрицательно. Это означает, что большему значению одной величины соответствует в среднем меньшее значение другой. Например, число пропусков занятий и успеваемость коррелированы отрицательно.
4. Если 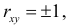 то из (2.14.4) следует, что
то из (2.14.4) следует, что 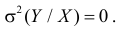 В этом случае разброса относительно линии регрессии нет. Между величинами существует линейная функциональная зависимость.
В этом случае разброса относительно линии регрессии нет. Между величинами существует линейная функциональная зависимость.
5. Из (2.14.4) следует, что 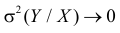 при
при 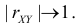 Значит, чем больше по модулю коэффициент корреляции, тем теснее прилегают значения Y к линии регрессии, тем меньше средний квадрат ошибки прогноза Y по наблюдаемому значению X. На рис. 2.14.4 для сравнения показан разброс положений случайной точки
Значит, чем больше по модулю коэффициент корреляции, тем теснее прилегают значения Y к линии регрессии, тем меньше средний квадрат ошибки прогноза Y по наблюдаемому значению X. На рис. 2.14.4 для сравнения показан разброс положений случайной точки 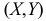 относительно линии регрессии при двух разных значениях коэффициента корреляции
относительно линии регрессии при двух разных значениях коэффициента корреляции 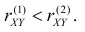
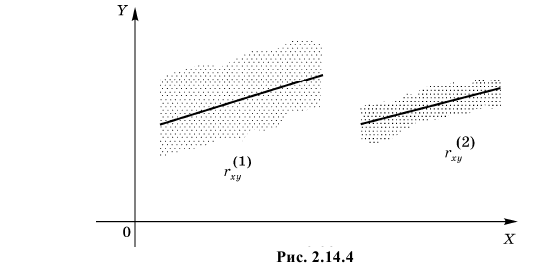
Коэффициент корреляции служит мерой линейной зависимости между величинами. Он показывает насколько статистическая зависимость близка к функциональной.
Отметим, что в силу (2.14.3) уравнение линии регрессии можно записать в виде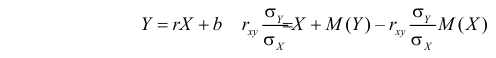
или
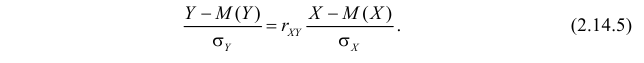
Пример №1
Случайные величины X и Y независимы и имеют одинаковое распределение с математическим ожиданием 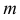 и дисперсией
и дисперсией 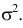
1) Найти коэффициент корреляции случайных величин 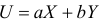 и
и 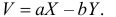
2) Найти коэффициент корреляции между случайными величинами 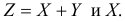
Решение. 1) По определению 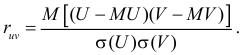 Найдем необходимые для вычисления
Найдем необходимые для вычисления 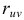 величины. По свойствам математического ожидания и дисперсии имеем:
величины. По свойствам математического ожидания и дисперсии имеем:
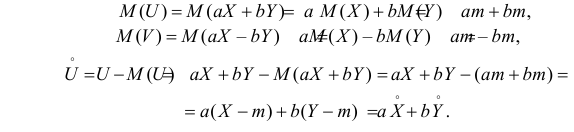
Аналогично, 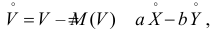
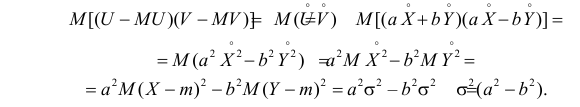
Так как X и Y независимы, то 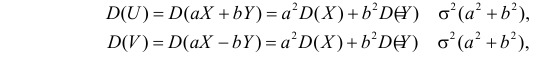
В результате имеем
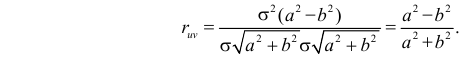
2) Вычислим величины, которые необходимы для использования формулы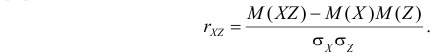
Так как X и Y независимы, то 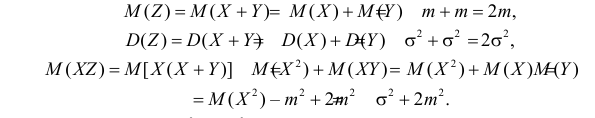
Поэтому 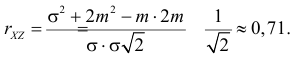
Ответ. 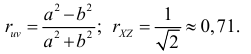
Пример №2
Равновозможны все положения случайной точки 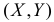 в треугольнике D с вершинами А(0,0), В(0,1) и С(2,1). Найти коэффициент корреляции случайных величин X и Y. Найти линию регрессии Y на X и оценить точность прогноза величины Y по наблюдаемому значению X.
в треугольнике D с вершинами А(0,0), В(0,1) и С(2,1). Найти коэффициент корреляции случайных величин X и Y. Найти линию регрессии Y на X и оценить точность прогноза величины Y по наблюдаемому значению X.
Решение. Равновозможность всех положений случайной точки 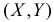 в треугольнике АВС (см. рис. 2.14.5) означает, что плотность вероятности
в треугольнике АВС (см. рис. 2.14.5) означает, что плотность вероятности 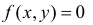 вне этого треугольника, а в точках треугольника постоянна.
вне этого треугольника, а в точках треугольника постоянна.
Площадь треугольника АВС равна 1. В точках треугольника положим 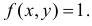 Тем самым соблюдено условие равенства единице объема, заключенного между функцией плотности вероятности и координатной плоскостью (напомним, что это является одним из отличительных свойств функции плотности вероятности системы двух случайных величин).
Тем самым соблюдено условие равенства единице объема, заключенного между функцией плотности вероятности и координатной плоскостью (напомним, что это является одним из отличительных свойств функции плотности вероятности системы двух случайных величин).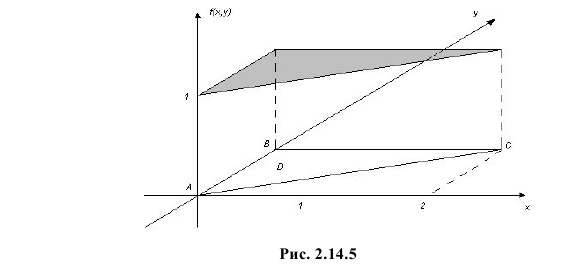
Маргинальные функции плотности вероятности величин X и Y равны соответственно:
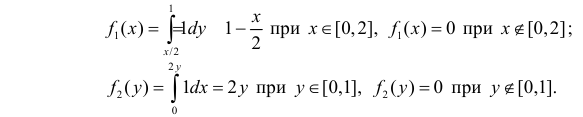
Вычислим величины, необходимые для использования формул (2.14.3) и (2.14.5): 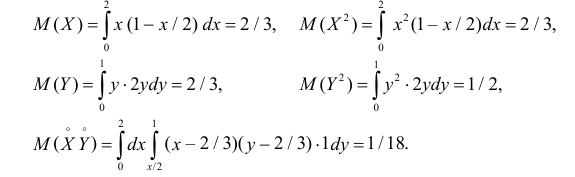
Тогда 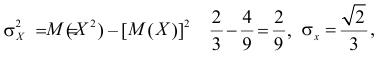
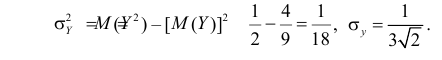
По формулам (2.14.3), (2.14.5) находим коэффициент корреляции 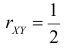 и уравнение линии регрессии
и уравнение линии регрессии 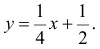 Если использовать эту линию регрессии для прогноза Y по известному значению X, то средний квадрат ошибки прогноза по формуле (2.14.4) равен
Если использовать эту линию регрессии для прогноза Y по известному значению X, то средний квадрат ошибки прогноза по формуле (2.14.4) равен 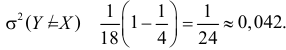
Ответ. 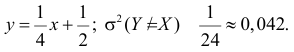
Пример №3
Подбрасывают два игральных кубика. Пусть X – число выпавших «пятерок», а Y – число нечетных очков. Найдите закон 149 распределения случайного вектора 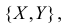 его математическое ожидание и дисперсионную матрицу. Найдите коэффициент корреляции
его математическое ожидание и дисперсионную матрицу. Найдите коэффициент корреляции 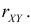
Решение. Если кубики однородны и симметричны, то вероятность выпадения каждой грани равна 1/6. Запишем сначала закон распределения случайного вектора 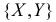 . Каждая из компонент вектора может принимать только значения 0, 1 и 2. Поэтому закон распределения можно представить в виде таблицы:
. Каждая из компонент вектора может принимать только значения 0, 1 и 2. Поэтому закон распределения можно представить в виде таблицы: 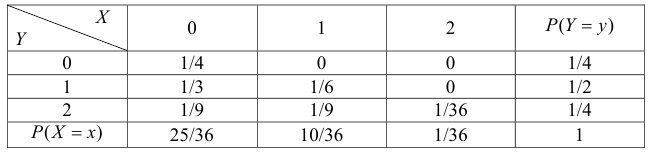
В клетках таблицы записаны вероятности 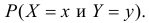 Например, 1
Например, 1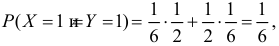 так как с вероятностью
так как с вероятностью 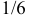 на первом кубике появится «5», а на втором кубике с вероятностью
на первом кубике появится «5», а на втором кубике с вероятностью 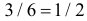 выпадет четное число, либо наоборот, на первом кубике – четное число, а на втором – «5». Или, например,
выпадет четное число, либо наоборот, на первом кубике – четное число, а на втором – «5». Или, например, 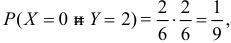 так как на каждом кубике должна выпасть нечетная цифра, но не «5». Вычислим числовые характеристики случайного вектора:
так как на каждом кубике должна выпасть нечетная цифра, но не «5». Вычислим числовые характеристики случайного вектора:
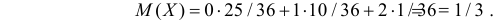
Заметим, что X имеет биномиальное распределение. Поэтому математическое ожидание можно было подсчитать проще: 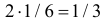 – произведение числа опытов на вероятность появления события в одном опыте. Аналогично,
– произведение числа опытов на вероятность появления события в одном опыте. Аналогично,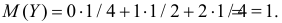 Для вычисления дисперсий вычислим предварительно математические ожидания квадратов величин:
Для вычисления дисперсий вычислим предварительно математические ожидания квадратов величин: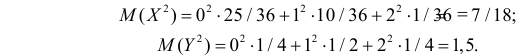
Тогда 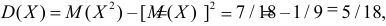
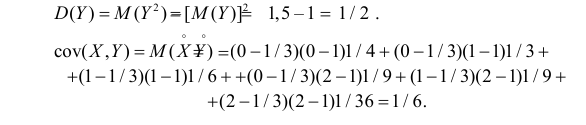
Дисперсионная матрица случайного вектора имеет вид 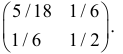
Коэффициент корреляции равен
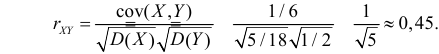
Ответ. 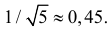
Замечание. Рассмотрим индикатор события A:
Известно, что 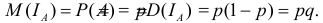 Силу зависимости между событиями A и B можно оценить по величине коэффициента корреляции индикаторов этих событий. По формуле (2.14.1) имеем
Силу зависимости между событиями A и B можно оценить по величине коэффициента корреляции индикаторов этих событий. По формуле (2.14.1) имеем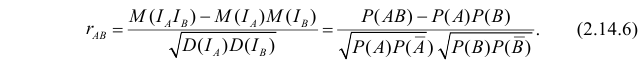
Коэффициент 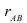 принимает значения в [-1;1], но есть некоторые особенности в трактовке значений коэффициента.
принимает значения в [-1;1], но есть некоторые особенности в трактовке значений коэффициента.
Если 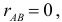 то события независимы и наоборот (вспомните, для случайных величин факт равенства коэффициента корреляции нулю не означал независимость случайных величин). Положительные значения коэффициента корреляции говорят о том, что появление одного события увеличивает вероятность появления другого. Например, из рис. 2.14.6 видно, что отношение площади области B к площади прямоугольника меньше, чем отношение площади области AB к площади области A. Поэтому факт появления события A увеличивает вероятность появления события B.
то события независимы и наоборот (вспомните, для случайных величин факт равенства коэффициента корреляции нулю не означал независимость случайных величин). Положительные значения коэффициента корреляции говорят о том, что появление одного события увеличивает вероятность появления другого. Например, из рис. 2.14.6 видно, что отношение площади области B к площади прямоугольника меньше, чем отношение площади области AB к площади области A. Поэтому факт появления события A увеличивает вероятность появления события B.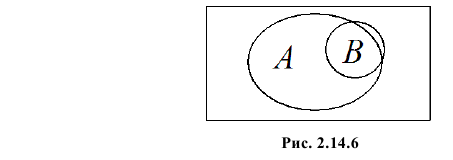
Чем ближе к плюс единице значение 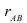 , тем в большей степени проявляется это увеличение. При
, тем в большей степени проявляется это увеличение. При 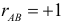 появление одного события всегда влечет появление другого. Если же
появление одного события всегда влечет появление другого. Если же 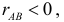 то появление одного события уменьшает вероятность появления другого. Например, из рис. 2.14.7 видно, что отношение площади области B к площади прямоугольника больше, чем отношение площади области AB к площади области A. Поэтому факт появления события A уменьшает вероятность появления события B. Значение
то появление одного события уменьшает вероятность появления другого. Например, из рис. 2.14.7 видно, что отношение площади области B к площади прямоугольника больше, чем отношение площади области AB к площади области A. Поэтому факт появления события A уменьшает вероятность появления события B. Значение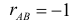 свидетельствует о том, что появление одного события исключает появление другого.
свидетельствует о том, что появление одного события исключает появление другого. 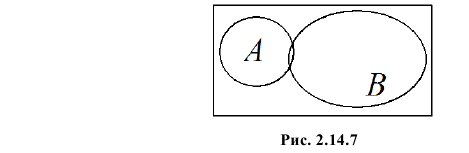
Пример №4
В одной урне четыре белых и два черных шара, а во второй два белых и три черных. Обозначим через A и B выбор белого шара соответственно из первой и второй урны. Ясно, что 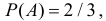 а 152 P( ) 2 / 5 B = и события независимы. Пусть при выборе из первой урны белого шара, его перекладывают во вторую урну и только потом выбирают из нее шар. Оценить силу зависимости между событиями A и B.
а 152 P( ) 2 / 5 B = и события независимы. Пусть при выборе из первой урны белого шара, его перекладывают во вторую урну и только потом выбирают из нее шар. Оценить силу зависимости между событиями A и B.
Решение. Для вычисления коэффициента корреляции воспользуемся формулой (2.14.6):
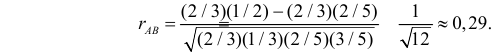
Заметим, что в случае добавлении не одного, а двух белых шаров во вторую урну этот коэффициент равен
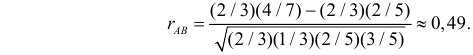
Ответ. 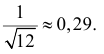
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |