
Корреляция - определение и вычисление с примерами решения
Содержание:
Понятие о корреляции:
Марксистская философия учит, что каждое явление природы и общества не возникает само по себе, отдельно от других, а находится в связи с другими явлениями, причем каждое из них представляет собой единство составляющих его частей и свойств. Для того чтобы познать какое-либо явление, необходимо изучить его не только во всех сложных взаимоотношениях с окружающими явлениями-факторами, но также во взаимосвязи всех его сторон.
Если всеобщая связь и взаимозависимость явлений составляют один из наиболее общих законов, то основной задачей науки является изучение этой взаимосвязи.
В математической статистике взаимосвязь явлений изучается методом корреляции. Термин корреляция происходит от английского слова correlation — соотношение, соответствие. Особенность изучения связи явлений методом корреляции состоит в том, что нельзя изолировать влияние посторонних факторов либо потому, что эти факторы неизвестны, либо потому, что их изоляция невозможна. Поэтому метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выяснить, какова была бы зависимость между результатом фактором, если бы посторонние факторы не изменялись и своим изменением не искажали основную зависимость. При этом небольшое число наблюдений не дает возможности обнаружить закономерность связи.
Первая задача корреляции заключается в выявлении на основе наблюдения над большим количеством фактов того, как изменяется в среднем результативный признак в связи с изменением данного фактора. Это изменение предполагает условие неизменности ряда других факторов, хотя искажающее влияние этих других факторов на самом деле имеет место. Вторая задача заключается в определении степени влияния искажающих факторов.
Первая задача решается нахождением уравнения связи.
Вторая задача решается при помощи различных показателей тесноты связи.
Такими показателями являются меры тесноты связи, найденные разными исследователями, а также коэффициент корреляции и корреляционное отношение.
Результативный и факториальный признаки
При изучении влияния одних признаков явлений на другие из цепи признаков, характеризующих данное явление, выделяются два признака — факториальный и результативный. Необходимо установить, какой из признаков является факториальным и какой результативным. В этом помогает прежде всего логический анализ.
Пример. Себестоимость промышленной продукции отдельного предприятия зависит от многих факторов, в том числе от объема продукции на данном предприятии. Себестоимость продукции выступает в этом случае как результативный признак, а объем продукции — как факториальный.
Другой пример. Чтобы судить о преимуществах крупных предприятий перед мелкими, рассмотрим, как увеличивается производительность труда рабочих крупных предприятий, и выявим зависимость производительности труда от увеличения размеров предприятия.
Таблица!
Группировка магазинов Министерства торговли по числу рабочих мест на 1 января 1960 г.1
Группы магазинов по числу рабочих мест Число магазинов Товарооборот в расчете на одного работника за квартал (в тыс. руб.)
Всего 68 375 117
Из них
с числом рабочих мест:
- с 1 19 893 109
- с 2 18 030 108
- с 3—4 16 508 108
- с 5—7 8 321 111
- с 8—10 2 868 118
- с 11 — 15 1 559 122
- с 16 и более 1 196 139
- J
Группировка показывает прямую зависимость производительности труда торговых работников, выражающуюся в товарообороте, приходящегося на одного работника, от размера магазина. Признак группировки — число рабочих мест — является факториальным, товарооборот — результативным признаком.
От размеров производства зависит также производительность оборудования, о чем свидетельствует следующая таблица:
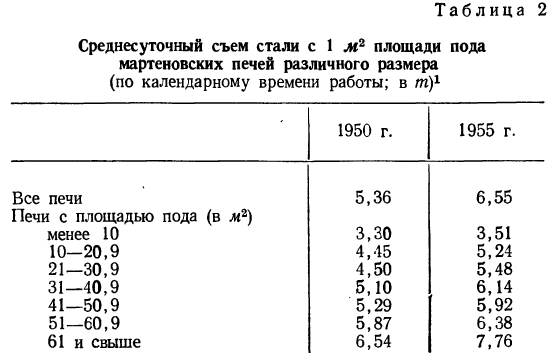
Из таблицы ясно видна связь между размерами печей и их производительностью. Эта связь прямая: чем крупнее печь, тем она производительнее.
Однако зависимость результативного признака (суточного съема стали) от факториального носит не обязательный характер. Если в общей массе мы наблюдаем эту связь, то в отдельных группах бывают и отступления от общей закономерности. Такие отступления—характерная особенность статистической связи вообще, о которой будет рассказано ниже.
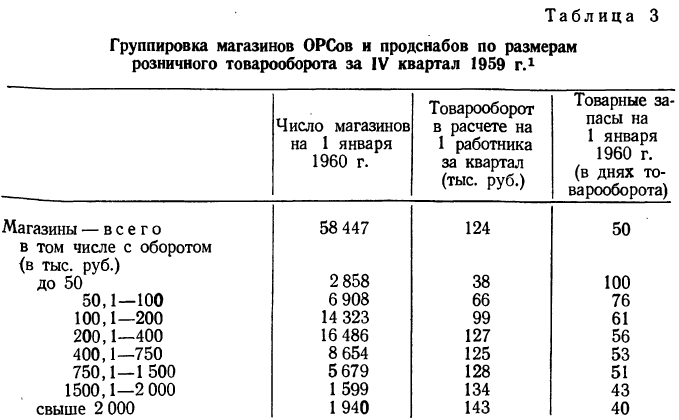
Группировки позволяют выявить и зависимость нескольких результативных признаков от одного факториального. Рассмотрим табл. 3.
В этой таблице мы видим зависимость двух результативных признаков: товарооборота на одного работника и товарных запасов—от размеров магазинов. Зависимость товарооборота от размеров магазина прямая, а зависимость товарных остатков от размеров магазина — обратная. В первом случае она растет с ростом размеров магазина, во втором уменьшается. Однако то и другое благоприятно.
Графическое изображение связи
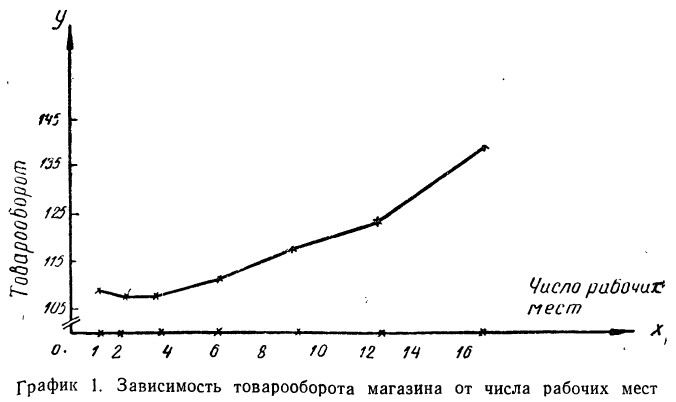
Графическое изображение изучаемых явлений позволяет не только установить наличие или отсутствие связи между ними, но и изучить характер этой связи, иначе говоря изучить форму связи и ее тесноту.
Имея перед собой числовые характеристики факториального и результативного признаков одного и того же явления, можно каждую пару чисел изобразить в виде точки на плоскости. Для этого на плоскости берем две взаимно перпендикулярные линии и образуем систему координат. В этой системе по оси абсцисс откладываем значения факториального признака, а по оси ординат— значения результативного признака. Каждая пара чисел дает при этом точку на плоскости координатного поля.
Возьмем, например, группировку магазинов по числу рабочих мест, данную на стр. 239, и будем откладывать число рабочих мест по горизонтальной оси (оси Ох), а товарооборот в расчете на одного работника — по вертикальной оси (оси Оу). Будем иметь ряд точек, соединив которые получим ломаную линию, которая называется ломаной регрессии (см. график 1).
Как видно из графика, с ростом числа рабочих мест в магазине растет и товарооборот, приходящийся на одного работника, что говорит о связи между этими признаками, причем связи прямой. График подчеркивает эту зависимость ходом ломаной линии из нижнего угла в верхний правый угол.
Такого же рода зависимость будем наблюдать на графике 2, изучая связь между величиной мартеновских печей по площади пода и среднесуточным съемом стали с 1 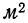 пода. Как и в предыдущем примере, факториальный признак — величину площади пода — будем откладывать на оси абсцисс, а результативный — среднесуточный съем стали с 1
пода. Как и в предыдущем примере, факториальный признак — величину площади пода — будем откладывать на оси абсцисс, а результативный — среднесуточный съем стали с 1 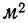 пода — на оси ординат.
пода — на оси ординат.
Здесь также ясно выраженная прямая зависимость между результативным и факториальным признаками.
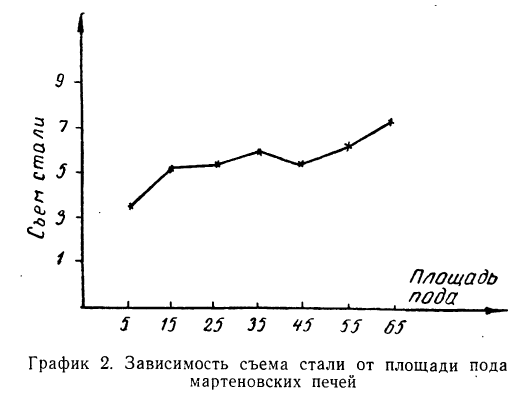
По-другому будет выглядеть график зависимости товарных запасов от размера товарооборота магазина.
Здесь мы наблюдаем ярко выраженную обратную связь между признаками: падение товарных запасов сопровождается ростом размера магазина по товарообороту.
Графический метод наглядно иллюстрирует зависимость, выявленную группировкой. Недостаток графического метода изучения связи заключается в том, что он позволяет выявить связь лишь между двумя признаками.
Функциональные и статистические связи
До сих пор говорилось о связях между явлениями и их признаками без объяснения формы и степени этих связей. В приведенных примерах связи носят логически обоснованный характер, но числовое выражение этих связей говорит о том, что они проявляются не всегда одинаково. В определенных случаях имеются отступления от наблюдаемых общих закономерностей. В приведенной на стр. 240 таблице о среднесуточном съеме стали с 1  пода печи наблюдается зависимость съема стали от размера печи по площади пода, но эта зависимость за 1955 г. искажена показателями 5-й группы, где съем стали значительно ниже, чем в 4-й группе. Если бы рассматривалась при этом каждая печь в отдельности, то это несоответствие установленному правилу зависимости проявлялось бы неоднократно. Но средние величины съема стали, вычисленные на основании данных довольно большого числа печей в группе, говорят о явно выраженной зависимости. Связи между явлениями, или их признаками. проявляющиеся в изменении в зависимости от одного признака характеристик распределения (из которых главная — средняя) другого признака, называются связями статистическими.
пода печи наблюдается зависимость съема стали от размера печи по площади пода, но эта зависимость за 1955 г. искажена показателями 5-й группы, где съем стали значительно ниже, чем в 4-й группе. Если бы рассматривалась при этом каждая печь в отдельности, то это несоответствие установленному правилу зависимости проявлялось бы неоднократно. Но средние величины съема стали, вычисленные на основании данных довольно большого числа печей в группе, говорят о явно выраженной зависимости. Связи между явлениями, или их признаками. проявляющиеся в изменении в зависимости от одного признака характеристик распределения (из которых главная — средняя) другого признака, называются связями статистическими.
Статистические связи характеризуются тем, что в них результативный признак не полностью определяется влиянием признака факториального. Это влияние проявляется лишь в среднем, а в отдельных случаях получаются результаты, даже противоречащие установленной связи.
В отличие от статистических связей связи функциональные характеризуются тем, что при таких связях факториальный признак полностью определяет величину результативного признака.
Функциональные связи почти не встречаются в явлениях общественной жизни, отличающихся сложностью и многообразием существующих и проявляющихся взаимосвязей. Но во многих явлениях в основе статистических связей лежат функциональные связи. Связь функциональная может показывать зависимость между результативным признаком и несколькими аргументами. Так, площадь прямоугольника зависит от длины его двух сторон, путь, проходимый телом, зависит от скорости его движения и времени движения и т. д.
Уравнение связи
Наблюдая статистическую связь между двумя признаками, математическая статистика стремится придать этой связи форму функциональной, т. е. связи, выражаемой при помощи математической функции.
На помощь приходит ее графическое изображение при отыскании нужной функции связи. При этом необходимо стремиться найти такую функцию, которая давала бы наименьшее отклонение от полученных при наблюдении значений их признаков, которая выражала бы основную зависимость, проявляющуюся в эмпирическом материале. Уравнение этой функции будет уравнением связи между результативным и факториальным признаками.
Уравнение связи находится с помощью способа наименьших квадратов, который требует, чтобы сумма квадратов отклонений эмпирических значений от значений, получаемых на основании уравнения связи, была минимальной.
Применение способа наименьших квадратов позволяет находить параметры уравнения связи при помощи решения системы так называемых нормальных уравнений, различных для связи каждого вида.
Чтобы отметить, что зависимость между двумя признаками выражается в среднем, значения результативного признака, найденные по уравнению связи, обозначаются 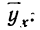
Зная уравнение связи, можно вычислить заранее среднее значение результативного признака, когда значение факториального признака известно. Таким образом, уравнение связи является методом обобщения наблюдаемых статистических связей, методом их изучения.
Применение той или иной функции в качестве уравнения связи разграничивает связи по их форме: линейную связь и криволинейную связь (параболическую, гиперболическую и др.).
Рассмотрим уравнения связи для зависимостей от одного признака при разных формах связи (линейной, криволинейной параболической, гиперболической) и для множественной связи.
Линейная зависимость
Уравнение связи как уравнение прямой 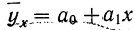 применяется в случае равномерного нарастания результативного признака с увеличением признака факториального. Такая зависимость будет зависимостью линейной (прямолинейной).
применяется в случае равномерного нарастания результативного признака с увеличением признака факториального. Такая зависимость будет зависимостью линейной (прямолинейной).
Параметры уравнения прямой линии 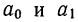 находятся путем решения системы нормальных уравнений, получаемых по способу наименьших квадратов:
находятся путем решения системы нормальных уравнений, получаемых по способу наименьших квадратов:
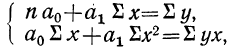
где n — число полученных при наблюдении пар взаимосвязанных величин; 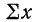 — сумма значений факториального признака;
— сумма значений факториального признака;
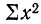 — сумма квадратов значений факториального признака;
— сумма квадратов значений факториального признака;
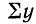 — сумма значений результативного признака;
— сумма значений результативного признака; 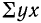 — сумма произведений значений факториального признака на значения результативного признака.
— сумма произведений значений факториального признака на значения результативного признака.
Примером расчета параметров уравнения и средних значений результативного признака 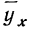 может служить следующая таблица, являющаяся результатом группировки по факториальному признаку и подсчета средних по результативному признаку.
может служить следующая таблица, являющаяся результатом группировки по факториальному признаку и подсчета средних по результативному признаку.
Группировка предприятий по стоимости основных средств и подсчет сумм необходимы для уравнения связи.
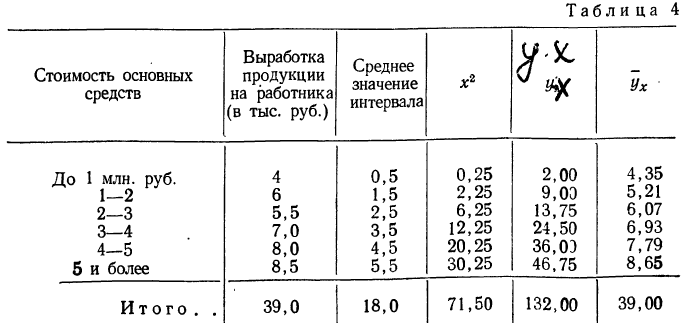
Из таблицы находим:  132,0. Строим систему двух уравнений с двумя неизвестными:
132,0. Строим систему двух уравнений с двумя неизвестными:
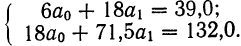
Поделив каждый член в обоих уравнениях на коэффициенты при 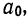 получим:
получим:
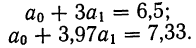
Вычтем из второго уравнения первое: 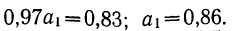 Подставив значения
Подставив значения 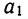 в первое уравнение
в первое уравнение 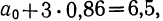 найдем
найдем 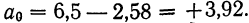
Уравнение связи примет вид: 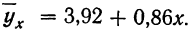 Подставив в это уравнение соответствующие х, получим значения результативного признака, отражающие среднюю зависимость у от х в виде корреляционной зависимости.
Подставив в это уравнение соответствующие х, получим значения результативного признака, отражающие среднюю зависимость у от х в виде корреляционной зависимости.
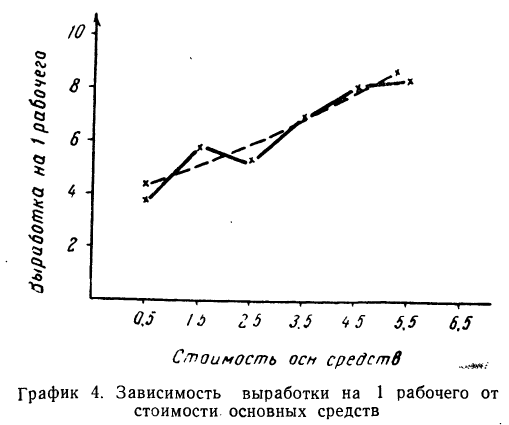
Заметим, что суммы, исчисленные по уравнению и фактические, равны между собой. Изображение фактических и вычисленных значений на графике 4 показывает, что уравнение связи отображает наблюденную зависимость в среднем.
Параболическая зависимость
Параболическая зависимость, выражаемая уравнением параболы 2-го порядка 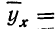
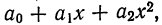 имеет место при ускоренном возрастании или убывании результативного признака в сочетании с равномерным возрастанием факториального признака.
имеет место при ускоренном возрастании или убывании результативного признака в сочетании с равномерным возрастанием факториального признака.
Параметры уравнения параболы 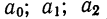 вычисляются путем решения системы 3 нормальных уравнений:
вычисляются путем решения системы 3 нормальных уравнений:
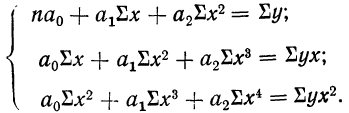
Возьмем для примера зависимость месячного выпуска продукции (у) от величины стоимости основных средств (х). Оба показателя округлены до миллионов рублей. Расчеты необходимых сумм приведем в таблице 5.
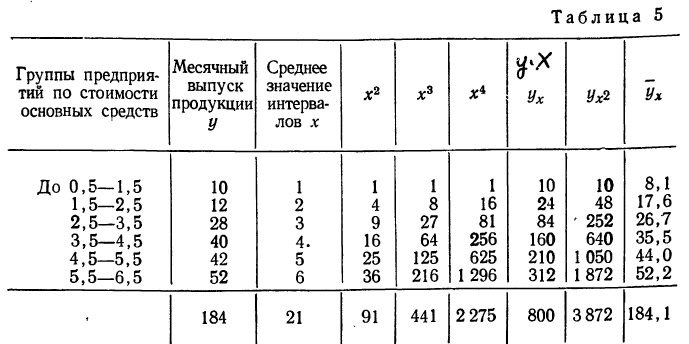
По данным таблицы, составляем систему уравнений:
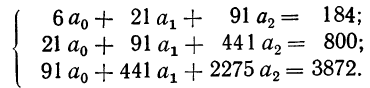
После деления всех уравнений на коэффициенты при 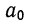 получим:
получим:
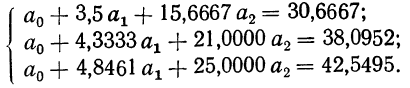
Вычтя из второго уравнения первое и из третьего второе, получим два новых уравнения с двумя неизвестными:
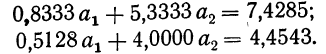
Полученные уравнения снова разделим на коэффициенты при 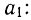
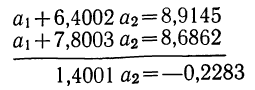
Следовательно, 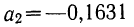
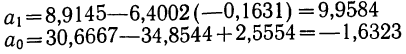
Запишем уравнение параболы, выражающей связь между х и у.
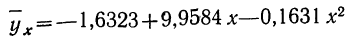
Графическое сопоставление опытных данных и данных расчета (см. график 5) показывает почти полное совпадение хода обеих линий, что говорит о хорошем воспроизведении опытных данных расчетными средними значениями результативного признака.
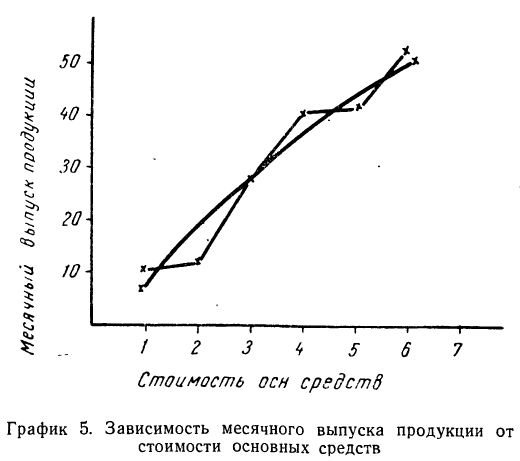
В практике изучения связи между признаками, кроме параболы 2-го порядка, применяются параболы и более высоких порядков. Чем выше порядок параболы, тем точнее он воспроизводит опытные данные.
Если уравнение связи представляет собой параболу 3-го порядка 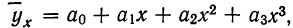 то система нормальных уравнений примет вид:
то система нормальных уравнений примет вид:
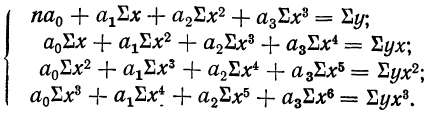
Имея соответствующие хну, можем составить Дополнительную расчетную таблицу по следующей схеме:

которая используется для нахождения нужных сумм. Решив систему 4 уравнений, найдем параметры 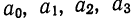 и, следовательно, уравнение связи.
и, следовательно, уравнение связи.
Уравнение гиперболы
Обратная связь указывает на убывание результативного признака при возрастании факториального. Такова линейная связь при отрицательном значении 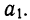 В ряде других случаев обратная связь может быть выражена уравнением гиперболы
В ряде других случаев обратная связь может быть выражена уравнением гиперболы 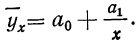
Параметры уравнения гиперболы 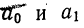 находятся из системы нормальных уравнений:
находятся из системы нормальных уравнений:
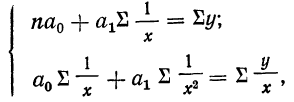
где 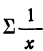 — сумма величин, обратных значениям факториального признака, а
— сумма величин, обратных значениям факториального признака, а 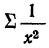 — сумма их квадратов.
— сумма их квадратов.
Примером расчета обратной связи по гиперболе может служить следующая таблица:
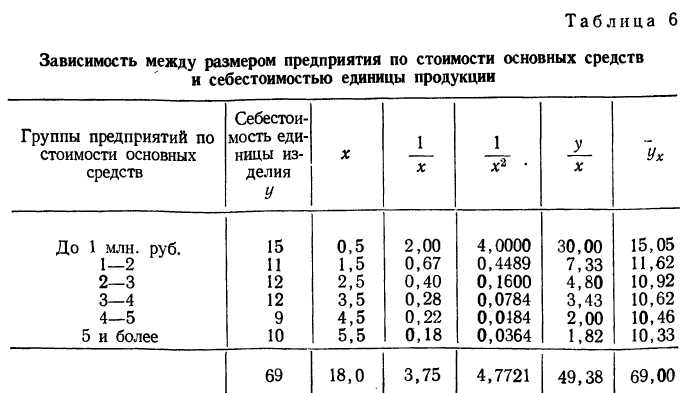
Составив по данным таблицы систему уравнений и разделив каждый член обоих уравнений на коэффициенты при а, получим:
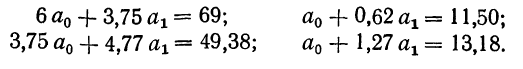
Находим вычитанием из второго уравнения первого величину 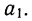
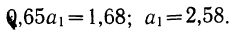
Подставив вместо 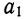 его значение, получим
его значение, получим 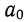
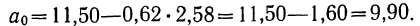
Запишем уравнение связи в общем виде 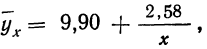 затем, подставив каждое значение х в уравнение, находим
затем, подставив каждое значение х в уравнение, находим 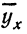 по любой строке таблицы. Строим ломаную по парам х и у и кривую по х и
по любой строке таблицы. Строим ломаную по парам х и у и кривую по х и 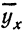 . Ломаная и кривая очень близки друг к другу.
. Ломаная и кривая очень близки друг к другу.
Корреляционная таблица
При большом объеме наблюдений, когда число взаимосвязанных пар велико, парные данные легко могут быть расположены в корреляционной таблице, являющейся наиболее удобной формой представления значительного количества пар чисел.
В корреляционной таблице один признак располагается в строках, а другой — в колонка таблицы. Число, расположенное в клетке на пересечении графы и колонки, показывает, как часто встречается данное значение результативного признака в сочетании с данным значением факториального признака.
Для простоты расчета возьмем небольшое число наблюдений на 20 предприятиях за средней месячной выработкой продукции на одного рабочего (тыс. руб. — у) и за стоимостью основных производственных средств (млн. руб. — х).
В обычной парной таблице эти сведения располагаются так: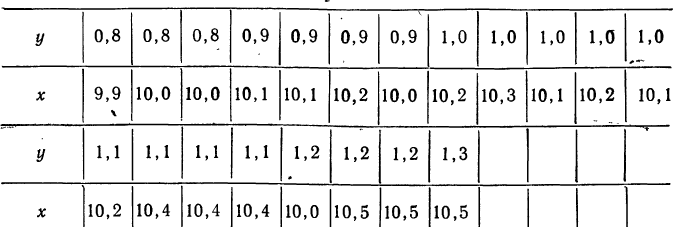
Сведем эти данные в корреляционную таблицу.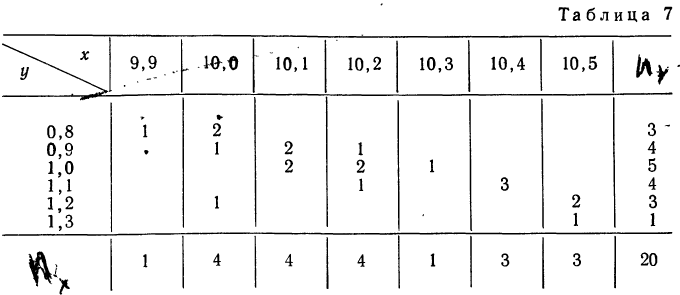
Итоги строк у показывают частоту признака 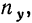 итоги граф х — частоту признака
итоги граф х — частоту признака 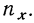 Числа, стоящие в клетках корреляционной таблицы, являются частотами, относящимися к обоим признакам и обозначаются
Числа, стоящие в клетках корреляционной таблицы, являются частотами, относящимися к обоим признакам и обозначаются 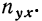
Корреляционная таблица даже при поверхностном знакомстве дает общее представление о прямой и обратной связи. Если частоты расположены по диагонали вниз направо, то связь между признаками прямая (при увеличивающихся значениях признака в строках и графах). Если же частоты расположены по диагонали вверх направо, то связь обратная.
Для предварительного суждения о связи по корреляционной таблице можно для каждого столбца рассчитать средние значения 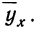 Так, в первом столбце х = 9,9, а
Так, в первом столбце х = 9,9, а 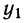 имеет лишь одно значение, равное 0,8. Найдем среднее значение для второго столбца. Оно будет равно:
имеет лишь одно значение, равное 0,8. Найдем среднее значение для второго столбца. Оно будет равно:
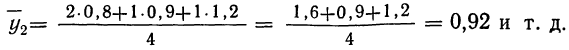
Следовательно, при 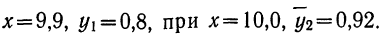 Выпишем все значения х и соответствующие им
Выпишем все значения х и соответствующие им 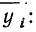

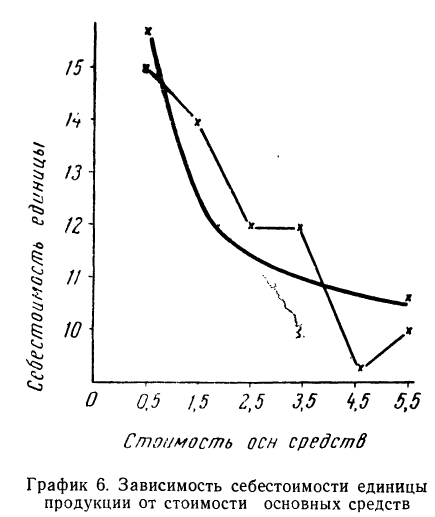
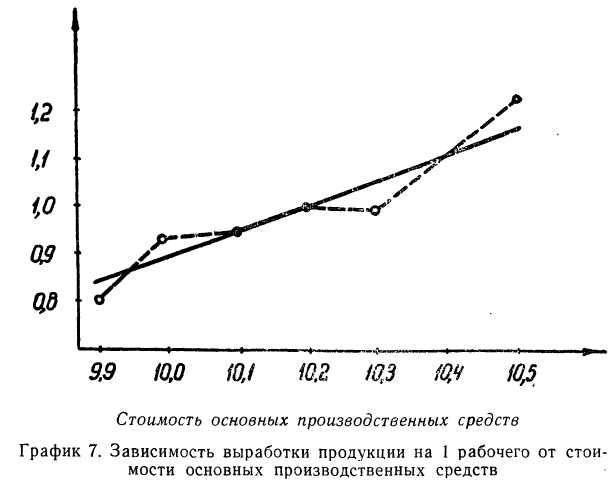
Зависимость, выраженная в таблице, более ярко и убедительно выступит в «ломаной регрессии», когда каждую пару чисел нанесем на график (см. график 7).
По корреляционной таблице можно вести расчеты параметров уравнения связи, как уравнения прямой, так и уравнений параболы и гиперболы. При этом необходимо учитывать, что сочетание каждой пары значений может встречаться не один, а несколько раз. Сами значения хну необходимо взвешивать, т. е. умножать на соответствующие частоты. Для самого признака х частота будет обозначаться 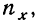 для признака
для признака 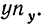 Частоту сочетаний обозначим
Частоту сочетаний обозначим 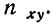
Ввиду сказанного мы можем систему нормальных уравнений написать так, чтобы были учтены веса. Тогда для линейной зависимости система нормальных уравнений примет вид:
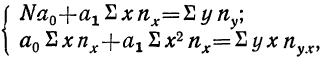
где N — число произведенных наблюдений (число пар). В приведенной корреляционной таблице N = 20. 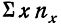 будет суммой произведений соответствующих х на их частоты. В данной таблице эта сумма составит:
будет суммой произведений соответствующих х на их частоты. В данной таблице эта сумма составит:
9,9 +10,0 • 4 +10,1 • 4 + 10,2 • 4 +10,3 • 1 +10,4 • 3 +10,5 • 3 = 204.
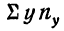 —сумма произведений у на соответствующие частоты. В нашем примере она равна:
—сумма произведений у на соответствующие частоты. В нашем примере она равна:
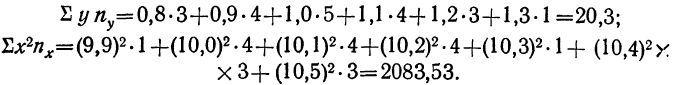
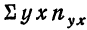 включает сумму произведений всех х на у и на
включает сумму произведений всех х на у и на 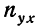 для тех клеток корреляционной таблицы, в которых записаны частоты. Рассчитаем суммы произведений для 1-й и 2-й строки
для тех клеток корреляционной таблицы, в которых записаны частоты. Рассчитаем суммы произведений для 1-й и 2-й строки
- Для 1 -и строки:
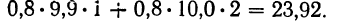
- Для 2-й строки:
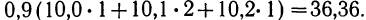
Нетрудно заметить, что в каждой строке у повторяется столько раз, сколько раз мы его суммируем, а, следовательно, у можно вынести за скобку.
- Для 1-й строки: 0,8 (9,9 • 1 +10,0 • 2) =23,92.
- Для 2-й строки:
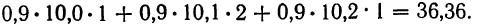
Следовательно, сумма произведений 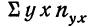 может быть записана при постоянном у, как
может быть записана при постоянном у, как 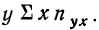 Заметим, что сумма произведений может быть записана и рассчитана как произведение
Заметим, что сумма произведений может быть записана и рассчитана как произведение 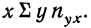
Продолжим расчет для последующих строк.
- Для 3-й строки
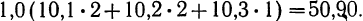
- Для 4-й строки
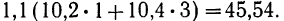
- Для 5-й строки
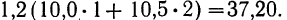
- Для 6-й строки
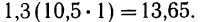
Общая сумма по всем строкам 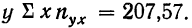
Система нормальных уравнений может быть записана по результатам подсчета в таком виде:
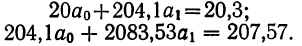
Для расчета параметров уравнения линейной связи делим каждое из уравнений на коэффициенты при 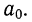
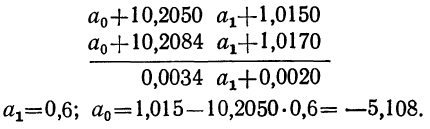
Уравнение связи 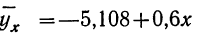 определяет среднюю зависимость выработки рабочего от стоимости основных средств. Вычислительная работа облегчается, если в самой корреляционной таблице путем записи дополнительных граф и строк производить нужные подсчеты для решения системы уравнений.
определяет среднюю зависимость выработки рабочего от стоимости основных средств. Вычислительная работа облегчается, если в самой корреляционной таблице путем записи дополнительных граф и строк производить нужные подсчеты для решения системы уравнений.
Число наблюдений N может быть подсчитано и по столбцу 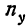 как его сумма. Она равна итогу по строке
как его сумма. Она равна итогу по строке 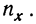 Для определения
Для определения 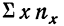 необходимо ввести новую строку
необходимо ввести новую строку 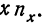 Итог этой строки и дает искомую сумму.
Итог этой строки и дает искомую сумму.
Следующая дополнительная строка 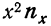 представляет возможность определить
представляет возможность определить 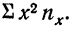 Далее,
Далее, 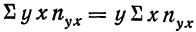 и может быть определена на основе расчета двух дополнительных граф:
и может быть определена на основе расчета двух дополнительных граф:
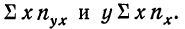
В корреляционной таблице (см. табл. 8) в последних строках дается расчет 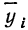 для построения ломаной регрессии
для построения ломаной регрессии 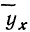 — для построения прямой (см. график 7).
— для построения прямой (см. график 7).
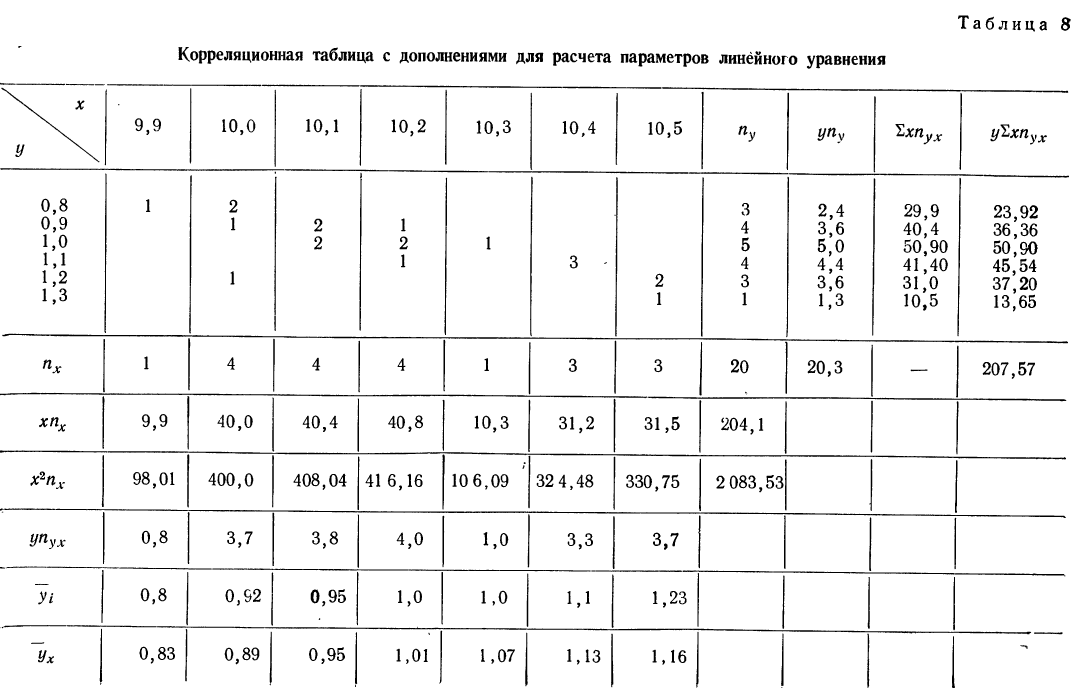
Корреляционная таблица позволяет вычислять уравнение связи для любой формы: прямой, параболы, гиперболы и др. Однако в подобной таблице видна зависимость результативного признака лишь от одного факториального.
Зависимость результативного признака от двух или более факториальных признаков носит название множественной связи.
Множественная связь
Исследование зависимости результативного признака от двух или нескольких факториальных признаков возможно при помощи уравнения множественной связи.
В простейшем уравнении множественной связи предполагается, что зависимость между признаками линейная. Сначала рассмотрим линейную зависимость результативного признака (у) от двух факториальных (х, z). Уравнение связи в этом случае выразится формулой 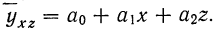 Параметры этого уравнения находятся при решении системы нормальных уравнений, получаемых для способа наименьших квадратов
Параметры этого уравнения находятся при решении системы нормальных уравнений, получаемых для способа наименьших квадратов
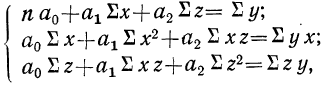
где п — число одновременных наблюдений по трем признакам;
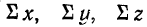 —суммы соответствующих значений по этим признакам.
—суммы соответствующих значений по этим признакам.
Все расчеты удобно сосредоточить в специальной таблице, как это делается в приводимом ниже примере.
Рассмотрим зависимость средней урожайности ячменя (у) на равных участках от количества внесенных минеральных удобрений (х) и количества выпавших в период цветения осадков (z).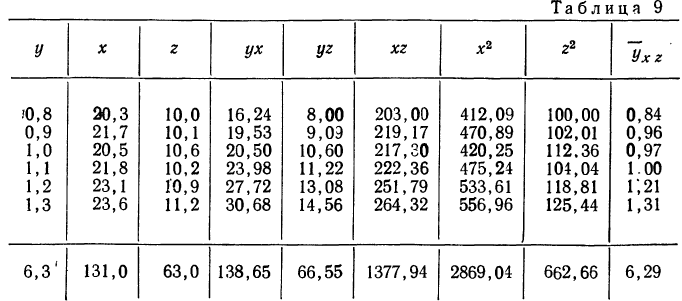
Средняя урожайность исчислялась по участкам с равным количеством внесенных удобрений и с равным количеством выпавших осадков.
Пользуясь данными таблицы, составляем систему трех уравнений:
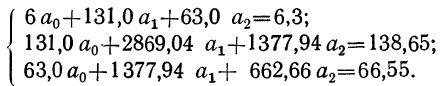
Поделив все члены уравнений на коэффициенты при 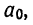 получим:
получим:
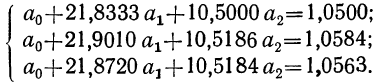
Вычитая из второго уравнения сначала первое, а затем третье, получим 2 уравнения с двумя неизвестными:
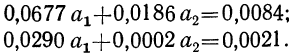
Делим каждый член обоих уравнений на коэффициенты при 
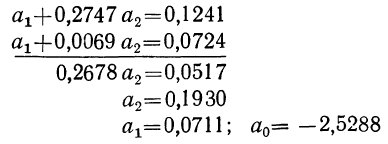
Уравнение связи, определяющее зависимость результативного признака (у) от двух факториальных
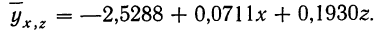
Вычислив по этому уравнению при соответствующих х и z величины 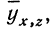 замечаем, что суммы опытных данных (y) и расчетных данных
замечаем, что суммы опытных данных (y) и расчетных данных 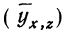 совпадают, а отдельные значения их мало отличаются друг от друга.
совпадают, а отдельные значения их мало отличаются друг от друга.
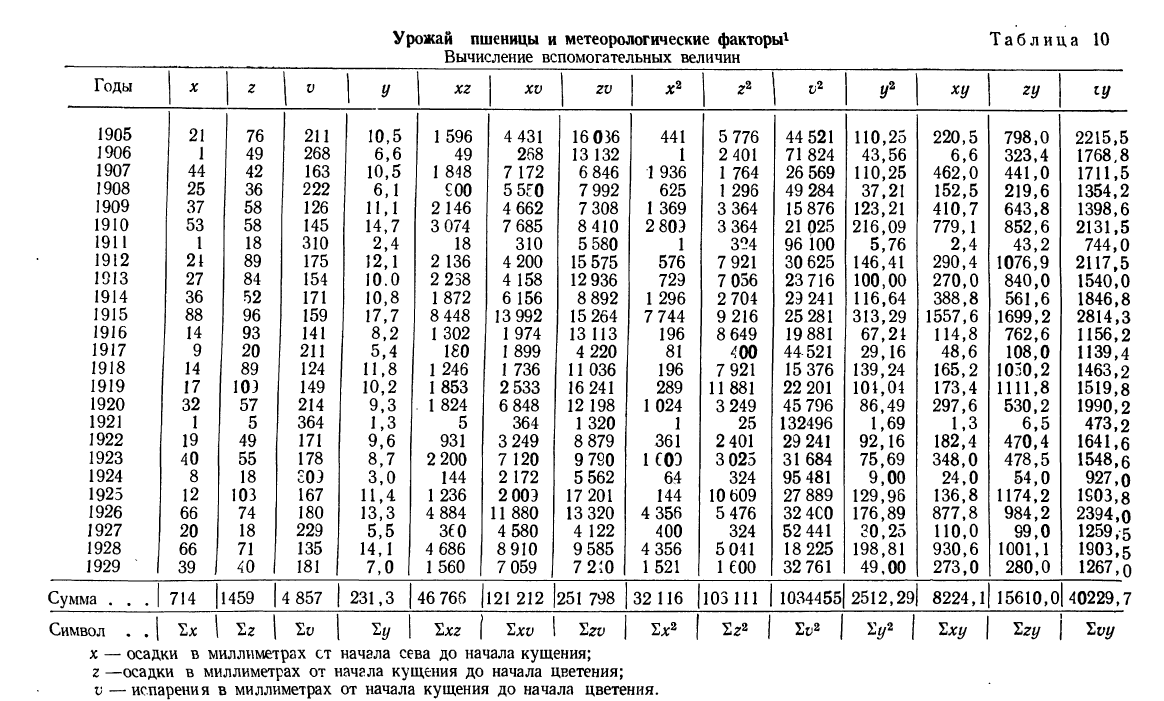
Найдем уравнение связи между урожайностью пшеницы на Безенчукской опытной станции и тремя факторами (х, z, v).
Статистические данные, полученные в результате наблюдения, и расчеты представлены в табл. 10, откуда возьмем необходимые данные для составления системы нормальных уравнений:

Следовательно,, корреляционное уравнение будет:
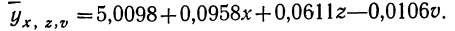
Расширив число факториальных признаков, можно найти уравнение множественной связи для 4, 5, 6 и т. д. признаков. При этом необходимо брать только такие признаки, которые оказывают существенное влияние на величину результативного признака, ибо учет несущественных, второстепенных признаков лишь увеличивает расчетную работу при нахождении уравнения связи, а не приближает к более полному изучению связи.
Если число факториальных признаков возрастает, возрастает и число членов уравнения связи. Так, для трех факториальных признаков линейное уравнение связи будет записано формулой:
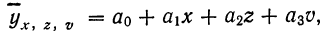
где параметры уравнения 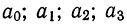 находятся путем решения системы четырех нормальных уравнений:
находятся путем решения системы четырех нормальных уравнений:
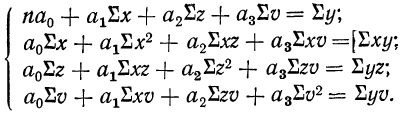
Построив соответствующую таблицу, получим в ней необходимые суммарные данные для приведенной системы уравнений (см. табл. 10).
Мерой существенности влияния того или иного факториального признака на результативный являются показатели тесноты связи.
В настоящем издании мы рассмотрим эмпирические меры тесноты связи, полученные разными исследователями, и меры тесноты связи, основанные на измерении вариации.
Эмпирические меры тесноты связи
Эмпирические меры тесноты связи позволяют оценить степень связи между явлениями или факторами, находящимися в зависимости один от другого. Эмпирические меры получены различными исследователями, занимавшимися статистической обработкой фактического материала. Они получены ранее, чем был открыт метод корреляции. Практическое пользование эмпирическими показателями довольно удобно.
К эмпирическим мерам тесноты относятся:
- а) коэффициент ассоциации:
- б) коэффициенты взаимной напряженности;
- в) коэффициент Фехнера;
- Г) коэффициент корреляции рангов;
Рассмотрим каждый из них.
а) Коэффициент ассоциации. Коэффициент ассоциации как мера тесноты связи применяется для изучения связи двух качественных признаков, состоящих только из двух групп. Для его вычисления строится четырехклеточная таблица корреляции, которая выражает связь между двумя явлениями, каждое из которых, в свою очередь, должно быть альтернативным, т. е. состоящим только из двух видов, качественно отличных друг от друга. Например, при изучении зависимости урожая от количества внесенных в почву удобрений выделяем по урожайности и по количеству внесенных удобрений лишь по две группы. При этом условии можно построить следующую четырехклеточную таблицу.
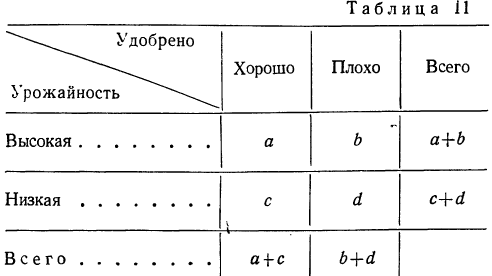
Числа, стоящие на пересечении строк и граф — a,b,c,d, показывают, сколько участков встречается с тем и другим количеством удобрений, внесенным в почву, с той и другой урожайностью.
Мера тесноты связи — коэффициент ассоциации — исчисляется по формуле:
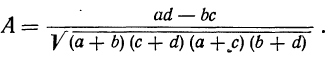
Заполнив клетки конкретными числовыми данными, получим следующую четырехклеточную таблицу, где числа, стоящие в клетках, — гектары посевов.

Коэффициент ассоциации равен: 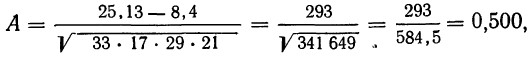
что говорит о достаточно тесной прямой связи между урожайностью и степенью удобрения почв.
Коэффициент ассоциации может иметь и отрицательные значения, когда ad б) Коэффициент взаимной сопряженности. Коэффициенты взаимной сопряженности являются мерами тесноты связи для качественных признаков, каждый из которых состоит более чем из двух групп. Для расчета коэффициентов взаимной сопряженности чаще всего применяются формулы, предложенные известным английским статистиком И. Пирсоном и видным русским статистиком А. А. Чупровым. Коэффициент взаимной сопряженности Пирсона исчисляется по формуле: По той же схеме исчисляется коэффициент взаимной сопряженности Чупрова: Приведем конкретный пример расчета взаимной сопряженности между урожайностью и поливом посевов. В каждой клетке таблицы записаны частоты, их квадраты, квадраты частот, деленные на сумму частот по столбцу. В итоговых столбцах записаны суммы частот, сумма результатов деления, а также результат деления нижнего числа на верхнее Исчислив коэффициент взаимной сопряженности по формуле Пирсона, получим; Формула Чупрова дает другой результат: в) Коэффициент корреляции рангов. При количественном выражении взаимосвязанных признаков теснота связи между ними может быть определена при помощи рангового коэффициента корреляции. Для определения рангового коэффициента корреляции ранжируем (записываем в возрастающем или убывающем порядке) все значения факториального признака и вместе с тем записываем соответствующие значения результативного признака. Другими словами, определяем ранг по обоим признакам, т. е. номер каждого признака в ранжированных рядах. Пример: В нижеприведенных рядах определены ранги по обоим признакам Для равных значений ранг находится путем деления суммы приходящихся на них рангов на число равных значений. Величина рангового коэффициента корреляции определяется по формуле: г) Коэффициент Фехнера. Коэффициент Фехнера основан на применении первых степеней отклонений всех значений взаимосвязанных признаков от средней величины по каждому признаку. Вслед за определением линейных отклонений от средней сравниваем знаки отклонения по одному и другому признакам. Обозначаем совпадения знаков отклонений через а, а несовпадение— через b. Найдя величину по i можно судить о степени тесноты связи между признаками. Продолжим предыдущий пример, дополнив его таблицей отклонений от средних по обоим признакам и предварительно рассчитав Величина i достаточно близка к величине рангового коэффициента корреляции. Вывод остается прежним: связь между признаками тесная. Если произведено измерение явления по двум признакам, то имеется возможность находить меры рассеяния (главным образом дисперсию) по результативному признаку для одних и тех же значений факториального признака. Дана, например, корреляционная таблица двух взаимозависимых рядов, в которых для простоты имеется лишь три значения факториального признака количества внесенных удобрений (х), а результативный признак—урожайность (у) — значительно колеблется. Каждая группа участков с разной урожайностью имела разное количество внесенных удобрений. Так, когда вносилось удобрений по 20 т, урожайность на разных участках была разной: на одном участке она составила 0,8 т, на двух участках — 0,9 г, на трех— 1,0 т и на одном — 1,1 т. Найдем среднюю урожайность и дисперсию по урожайности для этой группы участков Для группы участков с количеством внесенных удобрений 30,0 т средняя урожайность составит: Дисперсия равна: Вычислим аналогичные характеристики для группы участков получивших удобрений по 40 т: Из этих данных можно определить также средний урожай всех 20 участков, независимо от количества внесенных удобрений, т. е. общую среднюю: и меру колеблемости (дисперсию), средней урожайности групп •около общей средней. Эту дисперсию называют межгрупповой дисперсией и обозначают где Межгрупповая дисперсия для данного примера составит: Однако, кроме межгрупповой дисперсии, можно вычислить и дисперсию как показатель рассеяния за счет остальных факторов (если называть так все прочие факторы, кроме удобрений). Этот показатель явится средней (взвешенной) величиной из показателей рассеяния (дисперсий) по группам участков Для нашего примера: Это практически означает, что можно получить общую меру рассеяния (дисперсию) для всех 20 участков, если имеются сведения о средних и дисперсиях по группам участков, отличающихся количеством внесенных удобрений. Следовательно, общая дисперсия по урожайности для 20 участков составит: Формулы для исчисления межгрупповой и средней из групповых дисперсий можно сокращённо записать так: Расчет общей дисперсии, внутригрупповой и межгрупповой дисперсий позволяет делать некоторые выводы о мере влияния факториального признака на колеблемость признака результативного. Эта мера влияния находится при помощи корреляционного отношения: Корреляционное отношение показывает, какую долю в общей мере рассеяния (дисперсии) занимает дисперсия, возникающая за счет влияния Факториального признака. Для приведённого в предыдущем параграфе примера При изучении тесноты связи между двумя взаимозависимыми рядами применяется линейный коэффициент корреляции, который показывает, существует ли и насколько велика связь между этими рядами. Линейный коэффициент корреляции может принимать любые значения в пределах от —1 до +1. Если величина линейного коэффициента корреляции отрицательная, то это говорит об обратной связи между изучаемыми признаками; если она положительная — о прямой связи. Если коэффициент корреляции равен нулю, то связи между признаками нет. Если коэффициент корреляции равен единице (с любым знаком), то между признаками существует функциональная связь. Для расчета линейного коэффициента корреляции пользуются формулой: Рассчитаем величину линейного коэффициента корреляции по данным о зависимости, урожая у от количества внесенных удобрений (в баллах) х. Для этого построим таблицу, в которую введем и необходимые для расчета дополнительные графы. Однако число наблюдений (5) недостаточно для того, чтобы сделать вывод о тесноте связи. Для более точного суждения необходимо произвести значительное число испытаний. Как уже говорилось, при большом числе испытаний данные двух взаимозависимых рядов сводятся в корреляционную таблицу. В таком случае необходимо каждое значение признака находить как значение, взвешенное по числу его повторений. Тогда будем иметь: Линейный коэффициент корреляции служит мерой тесноты связи при линейной связи между признаками х и у. В случае криволинейной связи пользоваться линейным коэффициентом корреляции как мерой тесноты связи не всегда можно. Тогда пользуются уже известным из предыдущего изложения корреляционным отношением: Воспользуемся примером на стр. 247 и рассчитаем корреляционное отношение. Значения что говорит об очень тесной связи между признаками. Когда на результативный признак действует два факториальных, то в случае линейной связи ее теснота измеряется совокупным коэффициентом корреляции, исчисляемым по следующей формуле: Линейные коэффициенты корреляции между парами взаимосвязанных значений могут быть найдены по формулам: Исчислим линейные коэффициенты корреляции между парами признаков и совокупный коэффициент корреляции по данным о зависимости между объемом у, диаметром х и высотой z модельных деревьев, выбранных из Сурской лесной дачи Пинежского бассейна (табл. 19). Вычислим теперь совокупный коэффициент корреляции: Совокупный коэффициент корреляции показывает степень, тесноты связи между результативным признаком и совокупным влиянием двух факториальных признаков. В данном примере эта связь очень тесная. Если имеется 3 и более факториальных признака, то совокупный коэффициент корреляции рассчитывается по формуле Для оценки надежности полученного коэффициента корреляции определяют погрешность коэффициента корреляции, которую находят по формуле: Такая вероятностная оценка линейного коэффициента корреляции необходима в том случае, когда произведенное число измерений является как бы выборкой из большого числа возможных измерений. Величина В примере на стр. 268 полученный линейный коэффициент корреляции, равный 0,9, имеет ошибку: Гарантийный минимум будет равен 0,9—0,09 = 0,81, или 81%. Гарантийный максимум приближается к 100%,. Это означает, что при условиях данного опыта следует ожидать влияния количества внесенных удобрений на урожай не менее, чем на 81 процент. Так как число наблюдений здесь совсем небольшое, то находить отношение Кроме совокупного коэффициента корреляции, познавательное значение имеют частные коэффициенты корреляции, которые оценивают степень связи одного фактора с другим фактором, взятым в отдельности, при исключении влияния третьих факторов. Так, при линейной связи между у, х, z частный коэффициент корреляции у и х при исключенном влиянии z будет равен: Если исключить влияние фактора х, то частный коэффициент корреляции исчисляется по формуле: При нахождении коэффициентов корреляции по выборочным данным возникает вопрос о связи выборочного коэффициента корреляции с генеральным. Для нормальной корреляции (когда оба признака подчинены закону нормального распределения) связь между ними установлена Р. Фишером, который нашел распределение величины где Статистическими характеристиками z является средняя Когда выборочный коэффициент корреляции z находится в пределах Практически можно считать распределение Фишера нормальным. Оно позволяет решить следующие задачи: Решая первую задачу, необходимо иметь сведения о выборочном коэффициенте корреляции r, генеральном Пример: Пусть r = 0,55, Из нормального распределения критерия следует: Найдем: Следовательно, вероятность того, что существуют случайные значения коэффициента корреляции, отличающиеся от действительного коэффициента корреляции Пример: Для решения второй задачи допустим, что в двух выборках По приложению V найдем для В этом случае: Вероятность расхождений Пример: Для решения третьей задачи возьмем те же данные: По величине Подставив в формулу значение z = 0,46, найдем r = 0,43. Значит, если 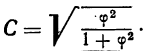
Входящая в эту формулу величина  называется показателем взаимной сопряженности и определяется суммой отношений квадратов частот каждой клетки таблицы, изображающей связь качественных признаков, к произведению частот итоговых соответствующего столбца и строки. Вычтя из этой суммы единицу, получим
называется показателем взаимной сопряженности и определяется суммой отношений квадратов частот каждой клетки таблицы, изображающей связь качественных признаков, к произведению частот итоговых соответствующего столбца и строки. Вычтя из этой суммы единицу, получим 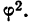
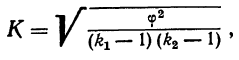
где 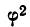 имеет одинаковое значение с
имеет одинаковое значение с 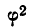 Пирсона и является показателем взаимной сопряженности,
Пирсона и является показателем взаимной сопряженности, 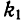 — число групп по столбцам таблицы,
— число групп по столбцам таблицы, 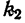 — число групп по строкам таблицы.
— число групп по строкам таблицы.
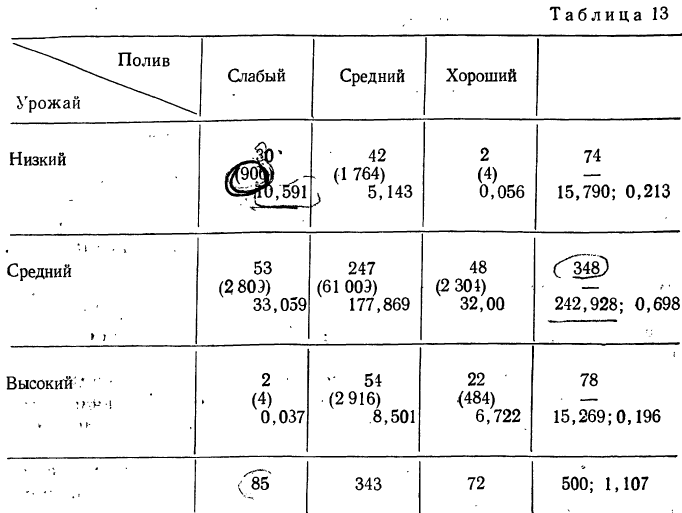
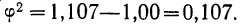
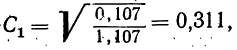
что говорит о значительной связи между урожайностью и поливом посевов. .
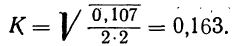
Коэффициент взаимной сопряженности Чупрова К является более гибким, поскольку он учитывает число образуемых по каждому признаку групп 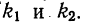 Поэтому результат 0,163 является более точным по сравнению с исчисленным коэффициентом взаимной сопряженности по формуле Пирсона.
Поэтому результат 0,163 является более точным по сравнению с исчисленным коэффициентом взаимной сопряженности по формуле Пирсона.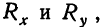 разности рангов
разности рангов 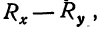 а также квадраты этих разностей
а также квадраты этих разностей 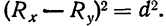
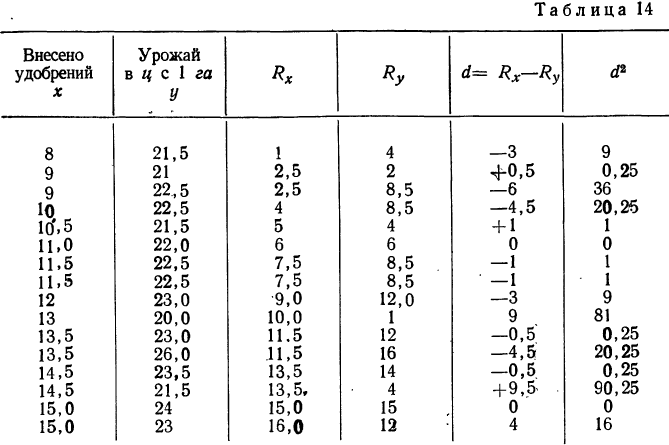
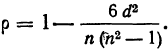
Если связь между признаками полная, прямая, то ранги по обоим признакам совпадут, тогда 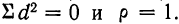 Если связь полная, обратная, то
Если связь полная, обратная, то 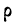 = —1. Если связи нет, то
= —1. Если связи нет, то 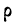 = 0. В приведенном примере
= 0. В приведенном примере 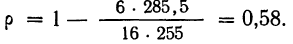 Следовательно, связь между изучаемыми признаками довольно тесная.
Следовательно, связь между изучаемыми признаками довольно тесная.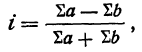
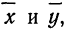 получим
получим 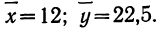

Корреляционное отношение


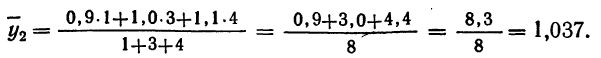
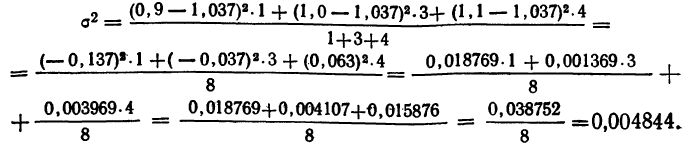
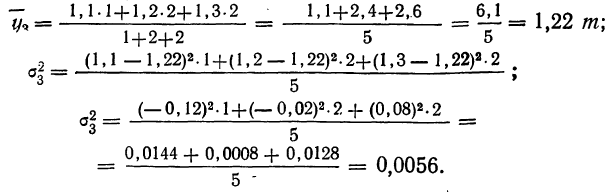
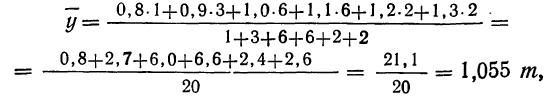
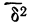
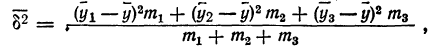
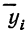 —средние урожайности по группам участков, отличающихся количеством внесенных удобрений;
—средние урожайности по группам участков, отличающихся количеством внесенных удобрений; 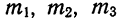 — численности групп.
— численности групп.
Межгрупповая дисперсия, показывает рассеяние, возникающее за счет факториального признака. В данном примере 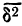 =0,010247 является показателем рассеяния урожайности, возникшего за счет разности в количестве внесенных удобрений.
=0,010247 является показателем рассеяния урожайности, возникшего за счет разности в количестве внесенных удобрений.
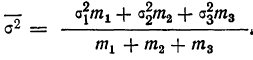
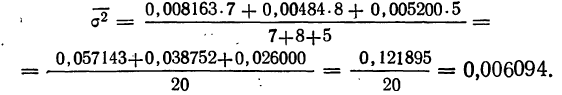
Выше было доказано, что сумма межгрупповой дисперсии и средней из дисперсий групп равна общей дисперсии: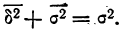
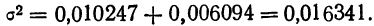
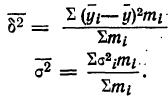
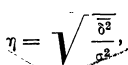
где 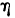 — показатель корреляционного отношения;
— показатель корреляционного отношения;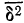 — межгрупповая дисперсия;
— межгрупповая дисперсия;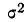 — общая дисперсия.
— общая дисперсия.
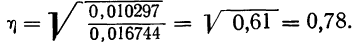
Значит, колеблемость по урожайности участков на 78% зависит от колеблемости количества внесенных удобрений. Иначе говоря, колеблемость по урожайности на 78% зависит от разности внесенных удобрений. Если бы устранить разность внесенных удобрений (иметь участки одинаково удобренные), то колеблемость по урожайности в значительной мере уменьшилась бы.Линейный коэффициент корреляции
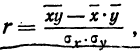
где 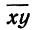 — среднее значение произведения х на у,
— среднее значение произведения х на у,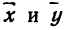 — средние значения соответствующих признаков;
— средние значения соответствующих признаков;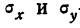 —средние квадратические отклонения, найденные по признаку х и по признаку у.
—средние квадратические отклонения, найденные по признаку х и по признаку у.
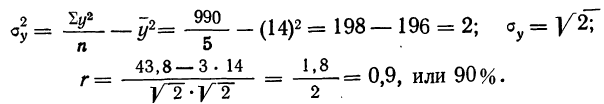
Линейный коэффициент корреляции показывает тесную связь, существующую между признаками х и у.
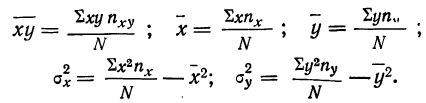
Вводя дополнительные данные в корреляционную таблицу и найдя необходимые показатели, рассчитаем линейный коэффициент корреляции по приведенной уже формуле.Теснота связи при криволинейной зависимости
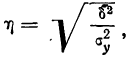
где 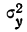 — дисперсия результативного признака;
— дисперсия результативного признака;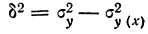 —величина
—величина 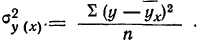
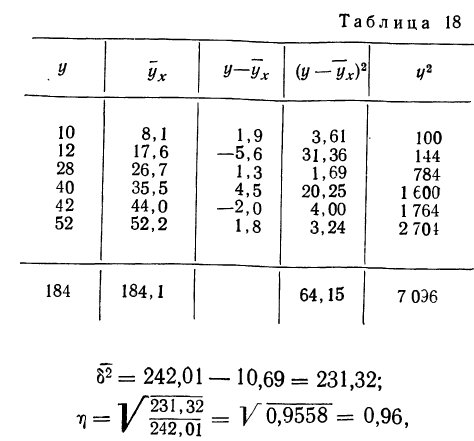
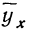 определены ранее. Дополним таблицу новыми необходимыми нам данными (см. табл. 18)
определены ранее. Дополним таблицу новыми необходимыми нам данными (см. табл. 18)
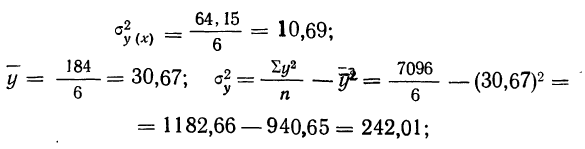
Совокупный коэффициент корреляции
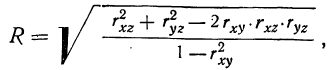
где r —линейные коэффициенты корреляции, а подстрочные знаки показывают, между какими признаками они исчисляются.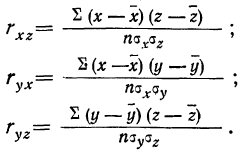
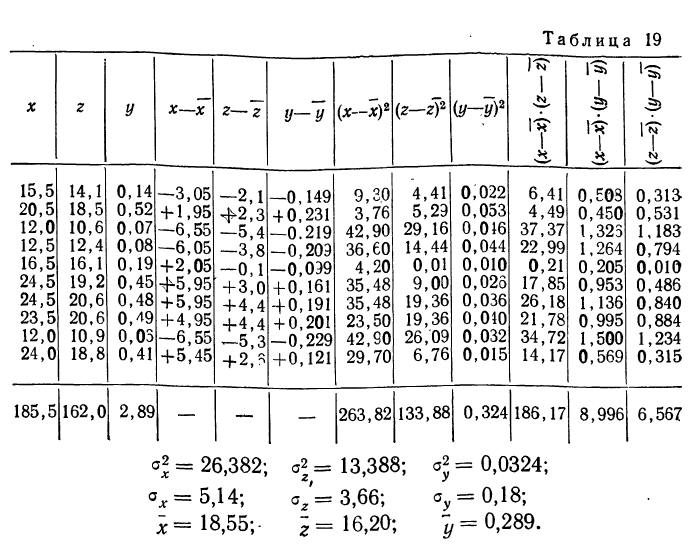
Найдем коэффициенты корреляции между х и z, у и х, у и z по приведенным выше формулам.

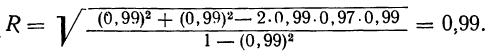
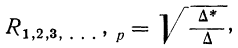
где 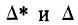 выражаются определителями:
выражаются определителями: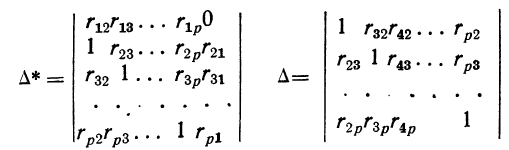
Определение надежности коэффициента корреляции
После расчета 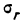 находят отношение
находят отношение 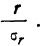 Если величина этого отношения превышает 3 при числе наблюдений, большем 50, то можно считать, что полученный коэффициент корреляции отображает истинное положение вещей.
Если величина этого отношения превышает 3 при числе наблюдений, большем 50, то можно считать, что полученный коэффициент корреляции отображает истинное положение вещей.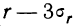 является гарантийным минимумом, а величина
является гарантийным минимумом, а величина 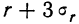 —гарантийным максимумом коэффициента корреляции.
—гарантийным максимумом коэффициента корреляции.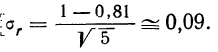
Ошибка возникает вследствие небольшого числа измерений.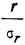 не имеет смысла.
не имеет смысла.Частные коэффициенты корреляции
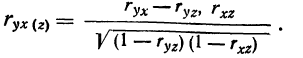 Для приведенного на стр. 271 примера:
Для приведенного на стр. 271 примера: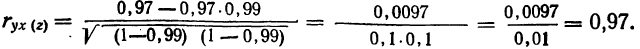
Частный коэффициент корреляции между у и х не зависит от значений фактора z. На этот коэффициент влияет только то, что за фактором z закрепляются постоянные значения, а не сами значения фактора z.
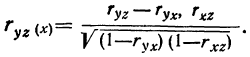
Этот коэффициент не зависит уже от значений фактора х, которые принимаются за постоянные величины, и определяет зависимость между у и z.Оценка выборочных коэффициентов корреляции
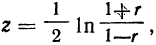 являющейся функцией выборочного коэффициента корреляции. Это распределение имеет формулу:
являющейся функцией выборочного коэффициента корреляции. Это распределение имеет формулу:
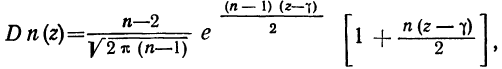
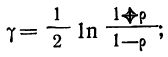
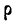 —коэффициент корреляции в генеральной совокупности.
—коэффициент корреляции в генеральной совокупности.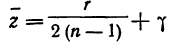 и среднее квадратическое отклонение
и среднее квадратическое отклонение 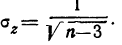
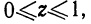 найденная функция изменяется в пределах
найденная функция изменяется в пределах 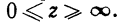
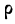 коэффициентами корреляции;
коэффициентами корреляции;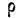 и числе наблюдений.
и числе наблюдений.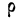 = 0,6, n — 25. На основании приложения V исчисляем:
= 0,6, n — 25. На основании приложения V исчисляем: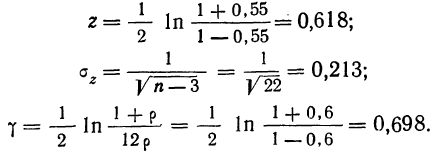
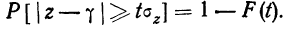
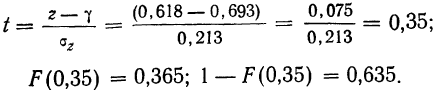
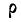 = 0,6, не менее, чем найденный нами коэффициент корреляции r=0,55, равна 0,635. Она говорит нам о допустимости гипотезы о случайном расхождении между r и
= 0,6, не менее, чем найденный нами коэффициент корреляции r=0,55, равна 0,635. Она говорит нам о допустимости гипотезы о случайном расхождении между r и 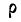 .
.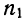 = 25 и
= 25 и 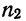 =19 коэффициенты корреляции
=19 коэффициенты корреляции 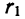 = 0,5 и
= 0,5 и 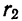 — 0,35.
— 0,35.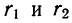 значения
значения 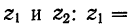
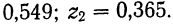
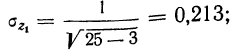
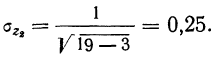
Исчислим разность 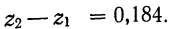 Эта разность также имеет нормальное распределение, дисперсия которого
Эта разность также имеет нормальное распределение, дисперсия которого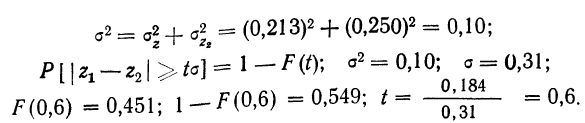
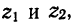 превышающих 0,184, имеет достаточно большое значение — 0,549. Поэтому исчисленные коэффициенты корреляции мало отличаются друг от друга.
превышающих 0,184, имеет достаточно большое значение — 0,549. Поэтому исчисленные коэффициенты корреляции мало отличаются друг от друга.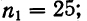
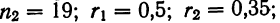 тогда
тогда 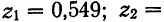
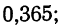
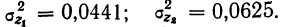 Среднее значение будет найдено как средняя арифметическая взвешенная:
Среднее значение будет найдено как средняя арифметическая взвешенная: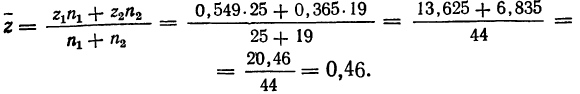
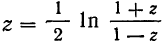 можно вычислить
можно вычислить 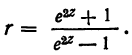
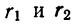 получились в результате выборок из одной генеральной совокупности, то наилучшим является коэффициент корреляции, равный 0,43.
получились в результате выборок из одной генеральной совокупности, то наилучшим является коэффициент корреляции, равный 0,43.
Рекомендую подробно изучить предметы: Ещё лекции с примерами решения и объяснением: