
Корень n-й степени из числа и его свойства с примерами решения
Содержание:
Корень n-й степени из числа a(n⩾2, n∈N)
Рассмотрим несколько задач.
Задача №1.
Кубический экологический резервуар для хранения воды имеет объем 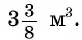
Решение:
Обозначим длину ребра куба через 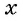
Ответ: длина ребра куба равна 1,5 м.
Задача №2.
Вкладчик положил 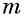 рублей на банковский счет, по которому сумма вклада увеличивается ежегодно на
рублей на банковский счет, по которому сумма вклада увеличивается ежегодно на 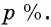 Через 4 года сумма на счете оказалась равной
Через 4 года сумма на счете оказалась равной 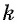 рублей. Определите процент
рублей. Определите процент 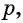 под который сделан вклад, если известен первоначальный вклад
под который сделан вклад, если известен первоначальный вклад 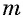 и сумма на счете
и сумма на счете 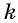 через 4 года.
через 4 года.
Решение:
Денежный вклад ежегодно увеличивается на 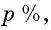 т. е. в
т. е. в 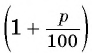 раз. Через 4 года он будет равен
раз. Через 4 года он будет равен 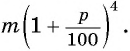 По условию задачи
По условию задачи 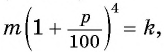 откуда
откуда 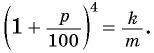 Для определения
Для определения 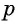 сначала нужно найти такое число, четвертая степень которого равна
сначала нужно найти такое число, четвертая степень которого равна 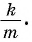
Многие задачи, как и рассмотренные, приводят к необходимости извлечения корня 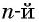 степени из действительного числа.
степени из действительного числа.
Определение:
Пусть 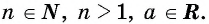 Корнем
Корнем 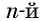 степени из числа
степени из числа 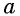 называется число,
называется число, 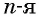 степень которого равна
степень которого равна 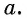
Например:
- корнем третьей степени из числа 125 является число 5, поскольку
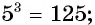
- корнем пятой степени из числа
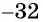 является число
является число 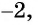 поскольку
поскольку 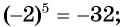
- корнями четвертой степени из числа 81 являются числа 3 и
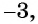 поскольку
поскольку 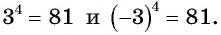
Из определения следует, что для нахождения корня 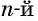 степени из действительного числа
степени из действительного числа 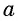 надо решить уравнение
надо решить уравнение 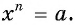
Выясним, сколько корней может иметь это уравнение в зависимости от 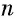 и от
и от 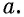
Корень четной степени из действительного числа
Рассмотрим уравнение 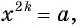 где
где 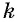 — натуральное число.
— натуральное число.
а) Если 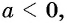 то уравнение не имеет корней, так как
то уравнение не имеет корней, так как 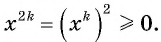
Следовательно, не существует корня четной степени из отрицательного числа.
б) Если 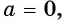 то уравнение
то уравнение 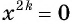 имеет единственный корень, равный нулю.
имеет единственный корень, равный нулю.
Значит, существует единственный корень четной степени из числа нуль.
в) Если 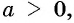 то уравнение
то уравнение 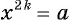 имеет два действительных корня: один положительный, а другой — противоположный ему — отрицательный.
имеет два действительных корня: один положительный, а другой — противоположный ему — отрицательный.
Рассмотрим функцию 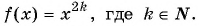 Мы рассматривали частный случай этой функции —
Мы рассматривали частный случай этой функции — 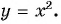 Свойства и график функции
Свойства и график функции 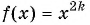 аналогичны свойствам и графику функции
аналогичны свойствам и графику функции 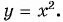
Так как функция 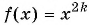 возрастает на множестве неотрицательных чисел и
возрастает на множестве неотрицательных чисел и 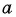 — значение, которое принимает эта функция
— значение, которое принимает эта функция 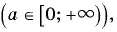 то уравнение
то уравнение 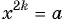 имеет единственный действительный корень при любом
имеет единственный действительный корень при любом 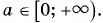
Пусть 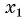 — положительный корень уравнения
— положительный корень уравнения 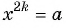 (рис. 116), значит, числовое равенство
(рис. 116), значит, числовое равенство 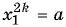 является верным. Так как
является верным. Так как 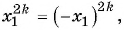 то верным является и числовое равенство
то верным является и числовое равенство 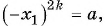 а значит, число
а значит, число 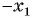 также является корнем уравнения
также является корнем уравнения 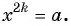
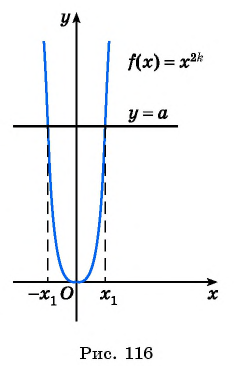
Таким образом, существует ровно два корня четной степени из положительного числа. Один из корней является положительным числом, а другой — противоположным ему числом.
Определение:
Арифметическим корнем 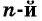 степени из числа
степени из числа 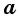 называется неотрицательное число,
называется неотрицательное число, 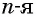 степень которого равна
степень которого равна 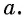
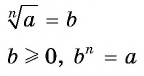
Например, 2 — арифметический корень четвертой степени из числа 16, поскольку 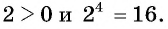
Арифметический корень 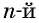 степени из числа
степени из числа 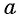 обозначается
обозначается 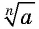 и читается: «арифметический корень
и читается: «арифметический корень 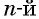 степени из числа
степени из числа 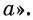 Число
Число 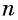 называется показателем корня, число
называется показателем корня, число 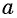 — подкоренным выражением.
— подкоренным выражением.
Можно, используя обозначения, записать 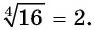 Читается: «арифметический корень четвертой степени из числа 16 равен 2». Слово «арифметический», как правило, опускается.
Читается: «арифметический корень четвертой степени из числа 16 равен 2». Слово «арифметический», как правило, опускается.
Корень второй степени из числа принято называть квадратным корнем (его свойства изучались в 8-м классе). Показатель корня второй степени при записи опускают. Например, корень второй степени из 13 обозначают 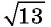 и говорят: «квадратный корень из 13».
и говорят: «квадратный корень из 13».
Действие нахождения арифметического корня 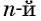 степени из числа
степени из числа 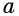 называется извлечением корня из числа.
называется извлечением корня из числа.
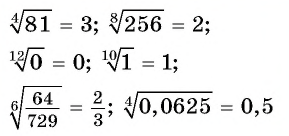
Пример №1
Выполните извлечение корня:
а) шестой степени из числа 64;
б) восьмой степени из числа 0,00000001.
Решение:
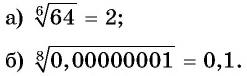
Такие числа, как 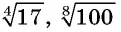 и т. п., являются иррациональными. С помощью десятичных приближений можно найти их значения с любой заданной степенью точности.
и т. п., являются иррациональными. С помощью десятичных приближений можно найти их значения с любой заданной степенью точности.
Корень нечетной степени из действительного числа
Рассмотрим уравнение 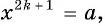 где
где 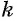 — натуральное число. Это уравнение имеет единственный корень.
— натуральное число. Это уравнение имеет единственный корень.
Рассмотрим функцию 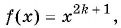 где
где 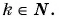 Эта функция является возрастающей на множестве всех действительных чисел и принимает все значения из промежутка
Эта функция является возрастающей на множестве всех действительных чисел и принимает все значения из промежутка 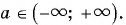
Так как функция 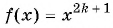 возрастает на
возрастает на 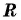 и
и 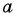 — значение, которое принимает эта функция
— значение, которое принимает эта функция 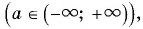 то уравнение
то уравнение 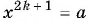 имеет единственный действительный корень при любом
имеет единственный действительный корень при любом 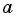 (рис. 117).
(рис. 117).
Существует единственный действительный корень нечетной степени из любого действительного числа.
Этот корень для неотрицательного числа 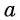 называется арифметическим и обозначается так же, как корень четной степени.
называется арифметическим и обозначается так же, как корень четной степени.
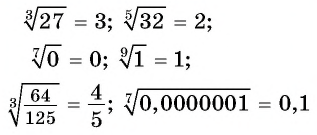
Например 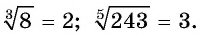
Такие числа, как 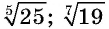 и т. п., являются иррациональными числами.
и т. п., являются иррациональными числами.
Корень третьей степени из числа называют кубическим корнем. Например, 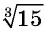 — кубический корень из 15.
— кубический корень из 15.
Корень нечетной степени из отрицательного числа принято записывать в виде 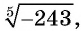 не называя его арифметическим корнем (читается: «корень пятой степени из числа -243»). А выражают его через арифметический корень из противоположного ему положительного числа.
не называя его арифметическим корнем (читается: «корень пятой степени из числа -243»). А выражают его через арифметический корень из противоположного ему положительного числа.
Например, 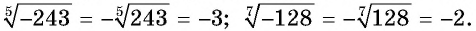
Пример №2
Определите, сколько существует корней:
а) четвертой степени из числа 25; б) пятой степени из числа 46; в) восьмой степени из числа -256; г) седьмой степени из числа -1.
Решение:
а) Так как 25 — положительное число, то существует два корня четвертой (четной) степени из числа 25;
б) так как существует только один корень нечетной степени из действительного числа, то существует только один корень пятой степени из числа 46;
в) так как число -256 — отрицательное, то не существует корня восьмой степени из числа -256, поскольку не существует корня четной степени из отрицательного числа;
г) так как существует только один корень нечетной степени из действительного числа, то существует только один корень седьмой степени из числа -1.
Пример №3
Назовите показатель корня, подкоренное выражение, прочитайте данное выражение:
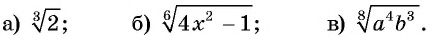
Решение:
а) Показатель корня равен 3, подкоренное выражение 2, данное выражение: «кубический корень из двух»;
б) показатель корня равен 6, подкоренное выражение 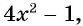 данное выражение: «корень шестой степени из разности
данное выражение: «корень шестой степени из разности 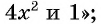
в) показатель корня равен 8, подкоренное выражение 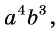 данное выражение: «корень восьмой степени из произведения степеней
данное выражение: «корень восьмой степени из произведения степеней 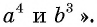
Пример №4
Какие из следующих равенств:
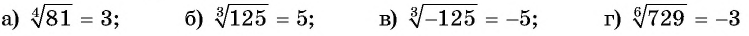 — являются верными?
— являются верными?
Решение:
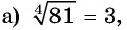 так как
так как 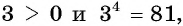 то по определению арифметического корня
то по определению арифметического корня 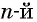 степени из числа равенство верное;
степени из числа равенство верное;
б) 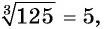 так как
так как 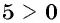 и
и 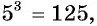 то по определению арифметического корня
то по определению арифметического корня 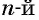 степени из числа равенство верное;
степени из числа равенство верное;
в) 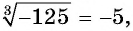 так как
так как 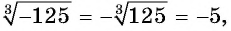 то равенство верное;
то равенство верное;
г) 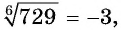 так как по определению арифметический корень четной степени из числа равен неотрицательному числу, то равенство неверное.
так как по определению арифметический корень четной степени из числа равен неотрицательному числу, то равенство неверное.
Пример №5
Какие из данных выражений:
 — не имеют смысла?
— не имеют смысла?
Решение:
а) Выражение 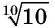 есть арифметический корень десятой степени из положительного числа 10, оно имеет смысл;
есть арифметический корень десятой степени из положительного числа 10, оно имеет смысл;
б) выражение 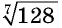 есть арифметический корень седьмой степени из положительного числа 128, оно имеет смысл;
есть арифметический корень седьмой степени из положительного числа 128, оно имеет смысл;
в) подкоренное выражение арифметического корня четвертой степени равно отрицательному числу -81, данное выражение не имеет смысла, так как не существует корня четной степени из отрицательного числа;
г) выражение 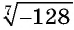 имеет смысл, так как существует корень нечетной степени из отрицательного числа.
имеет смысл, так как существует корень нечетной степени из отрицательного числа.
Пример №6
Сколько корней имеет уравнение:
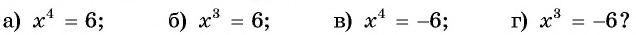
Решение:
а) Уравнение имеет два корня 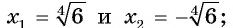
б) уравнение имеет один корень 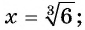
в) уравнение не имеет корней;
г) уравнение имеет один корень 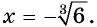
Пример №7
Решите уравнение:

Решение:

Ответ: -5; 5.
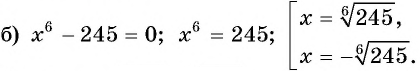
Ответ: 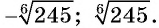
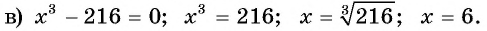
Ответ: 6.
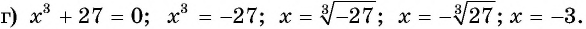
Ответ: -3.
Свойства корней n-й степени (n>1, n∈N)
Рассмотрим два свойства корней 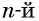 степени, аналогичные свойствам квадратных корней.
степени, аналогичные свойствам квадратных корней.
Свойство 1.
Корень  степени из произведения неотрицательных множителей равен произведению корней
степени из произведения неотрицательных множителей равен произведению корней 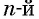 степени из этих множителей:
степени из этих множителей:
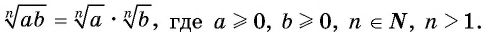
Свойство 2.
Корень 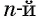 степени из частного равен частному корней
степени из частного равен частному корней 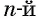 степени делимого и делителя, если делимое — неотрицательное число, а делитель — положительное число:
степени делимого и делителя, если делимое — неотрицательное число, а делитель — положительное число:
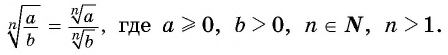
Докажем свойство 1 для корней 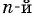 степени из произведения двух множителей:
степени из произведения двух множителей: 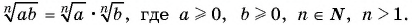
Доказательство:
При доказательстве используем определение арифметического корня 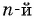 степени из числа и свойства степени с целым показателем. Обозначим
степени из числа и свойства степени с целым показателем. Обозначим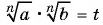 и покажем, что
и покажем, что 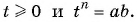
1) По определению арифметического корня 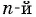 степени из числа имеем:
степени из числа имеем: 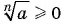 и
и 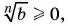 а так как произведение двух неотрицательных множителей есть число неотрицательное, то
а так как произведение двух неотрицательных множителей есть число неотрицательное, то 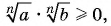 значит,
значит, 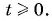
2) По свойству степени с целым показателем получим: 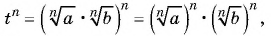 а по определению корня
а по определению корня 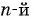 степени из числа
степени из числа 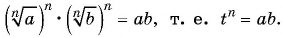
Таким образом, свойство доказано.
Свойство 2.
Докажите самостоятельно.
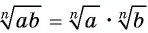
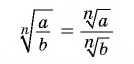
Пример №8
Вычислите:
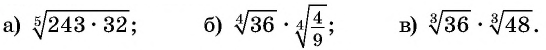
Решение:
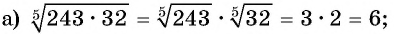
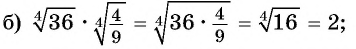
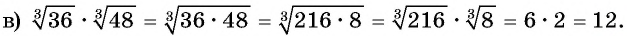
Пример №9
Вычислите:

Решение:
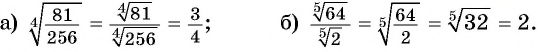
Свойство 3.
Значение корня из степени не изменится, если и показатель корня, и показатель подкоренного выражения умножить на одно и то же натуральное число или разделить на их общий делитель:
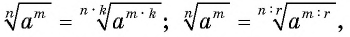
где 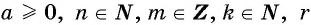 — общий натуральный делитель чисел
— общий натуральный делитель чисел 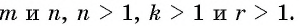
Докажем, что 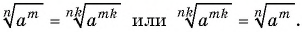 Доказательство проведем на основании определения корня степени
Доказательство проведем на основании определения корня степени 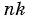 из числа
из числа 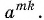 Обозначим
Обозначим 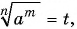 покажем, что
покажем, что 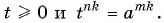 Очевидно, что
Очевидно, что 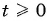 по определению арифметического корня.
по определению арифметического корня.
Покажем, что 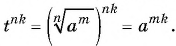 По свойству степени с целым показателем и
По свойству степени с целым показателем и
определению корня справедливы равенства: 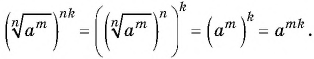
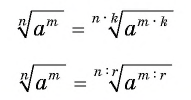
Пример №10
Упростите выражение
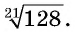
Решение:
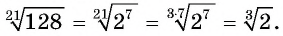
Свойство 4.
Чтобы извлечь корень 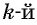 степени из корня
степени из корня 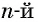 степени из неотрицательного числа, достаточно извлечь корень степени
степени из неотрицательного числа, достаточно извлечь корень степени 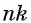 из этого числа:
из этого числа: 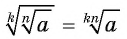 Для любых натуральных
Для любых натуральных 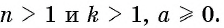 Для доказательства достаточно показать, что
Для доказательства достаточно показать, что 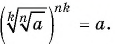
По свойству степени с натуральным показателем имеем: 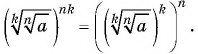 По определению корня получим:
По определению корня получим: 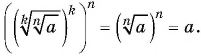 Свойство доказано.
Свойство доказано.
Пример №11
Упростите выражение
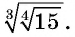
Решение:
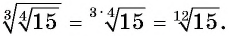
Свойство 5.
Для любого действительного 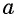 и натурального
и натурального 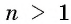 справедливо равенство
справедливо равенство 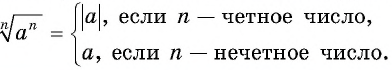
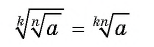
Действительно, если 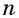 — четное, то
— четное, то 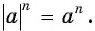 Если
Если 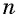 — нечетное, то
— нечетное, то 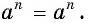 Таким образом, на основании определения корня
Таким образом, на основании определения корня 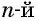 степени свойство доказано.
степени свойство доказано.
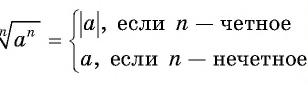
Пример №12
Вычислите:

Решение:
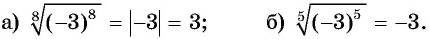
Пример №13
Найдите значение выражения:
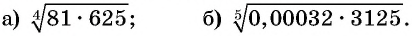
Решение:
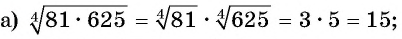
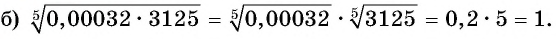
Пример №14
Вычислите:
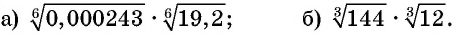
Решение:
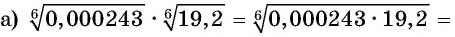
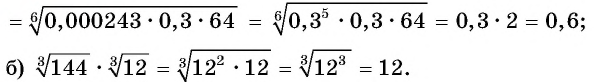
Пример №15
Найдите значение выражения:

Решение:
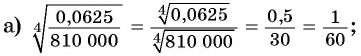
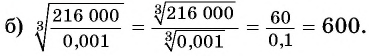
Пример №16
Найдите значение выражения:
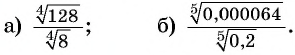
Решение:
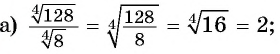
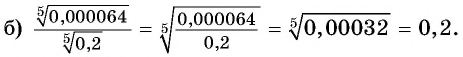
Пример №17
Упростите выражение:
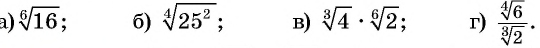
Решение:
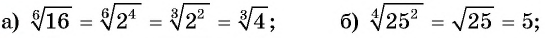
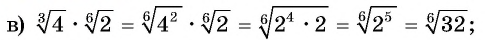

Пример №18
Упростите выражение:
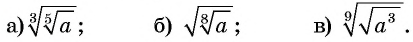
Решение:
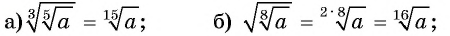
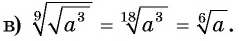
Пример №19
Найдите значение выражения:

Решение:
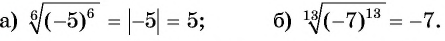
Пример №20
Замените выражение на тождественно равное ему:

Решение:
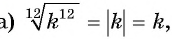 так как
так как 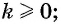
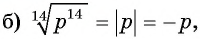 так как
так как 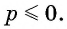
Применение свойств корней n-й степени для преобразования выражений
Вынесение множителя за знак корня
При выполнении преобразований иррациональных выражений, содержащих корни 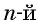 степени, подкоренные выражения раскладываются на множители, некоторые из которых представляют собой степень с показателем, равным показателю корня. Тогда можно выполнить действие, которое называется вынесением множителя за знак корня.
степени, подкоренные выражения раскладываются на множители, некоторые из которых представляют собой степень с показателем, равным показателю корня. Тогда можно выполнить действие, которое называется вынесением множителя за знак корня.
Вынесем множитель за знак корня в выражении 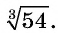 . Для этого число 54 представим в виде произведения двух множителей, один из которых является кубом некоторого выражения.
. Для этого число 54 представим в виде произведения двух множителей, один из которых является кубом некоторого выражения.
Тогда 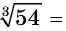
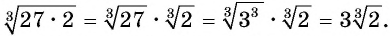
В этом случае говорят, что множитель 3 вынесли за знак корня.
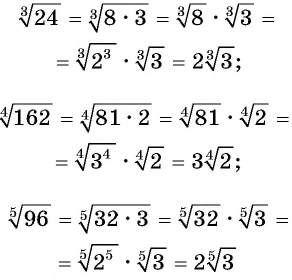
Чтобы вынести множитель за знак корня, нужно:
- Представить подкоренное выражение в виде произведения, содержащего степени выражений с показателем, равным показателю корня.
- Применить свойство корня из произведения.
- Найти корень
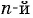 степени из выражения в степени
степени из выражения в степени 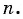
- Записать произведение полученного множителя и корня.
Вынесите множитель за знак корня в выражении 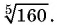
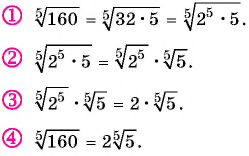
Внесение множителя под знак корня
При выполнении вычислений и преобразований, сравнении значений выражений иногда нужно выполнить действие, обратное действию вынесения множителя за знак корня. Оно называется внесением множителя под знак корня.
Внесем множитель 2 под знак корня в выражении 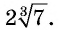
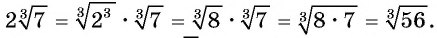
В выражении 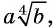 где
где 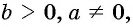 , внесем множитель
, внесем множитель 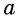 под знак корня:
под знак корня:
Если 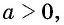 то
то 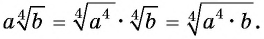
Если 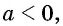 то
то 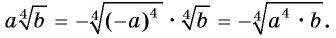
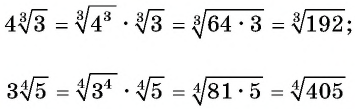
Чтобы внести множитель под знак корня, нужно:
- Представить неотрицательный множитель в виде корня
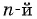 степени из
степени из 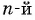 степени этого множителя.
степени этого множителя. - Произведение корней заменить корнем из произведения.
- Записать корень из произведения.
- Внесите множитель под знак корня в выражении
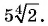
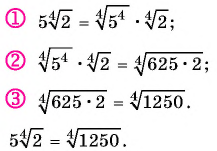
Пример №21
Найдите сумму 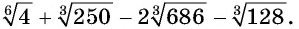
Решение:
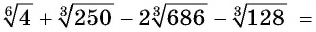
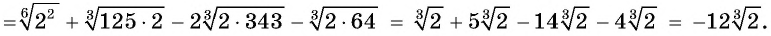
Пример №22
Упростите выражение 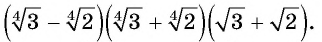
Решение:
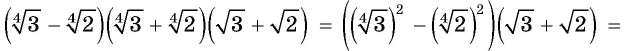
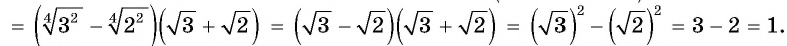
Пример №23
Разложите на множители 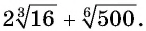
Решение:
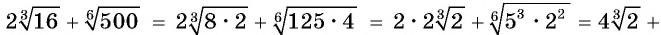
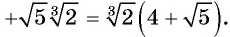
Пример №24
Сократите дробь 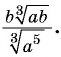
Решение:
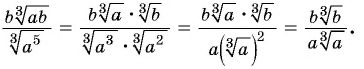
Избавление от иррациональности в знаменателе дроби
Если в знаменателе дроби содержатся выражения с корнями, выполняют преобразования, которые приводят к дробям без выражений с корнями в знаменателе. Традиция такого преобразования корней, с одной стороны, связана с приближенными вычислениями, а с другой — с более удобным (рациональным) упрощением выражений.
Пример №25
Избавиться от корня в знаменателе дроби 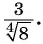
Решение:
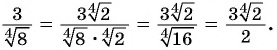
Пример №26
Избавиться от иррациональности в знаменателе дроби
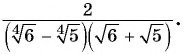
Решение:
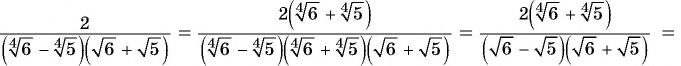
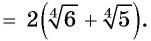
Пример №27
Вынесите множитель за знак корня:
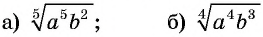 при
при 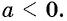
Решение:
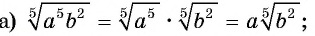
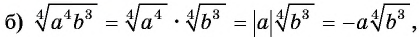 так как
так как 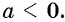
Пример №28
Внесите множитель под знак корня:

Решение:
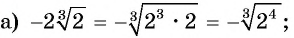
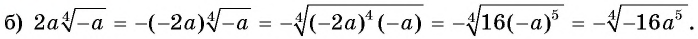
Пример №29
Упростите выражение:
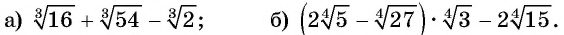
Решение:
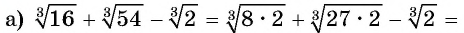
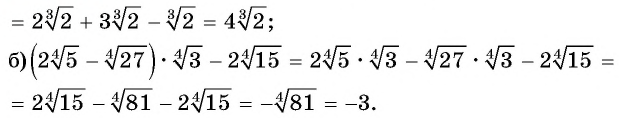
Пример №30
Выполните действия: 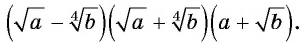
Решение:
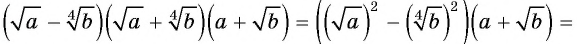
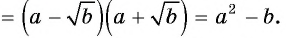
Пример №31
Сократите дробь 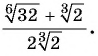
Решение:
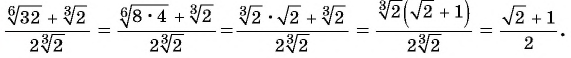
Пример №32
Избавьтесь от иррациональности в знаменатели дроби 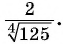
Решение:
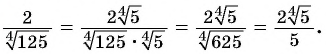
Пример №33
Упростите выражение 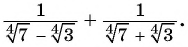
Решение:
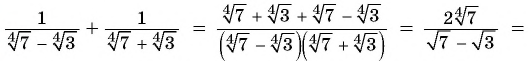
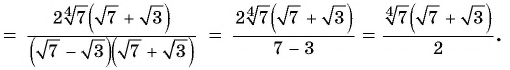
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |