
Корень из числа - нахождение и вычисление с примерами решения
Содержание:
Вам уже известно, что уравнение
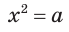
при неотрицательном значении а имеет два корня:
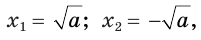
где выражение 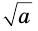 обозначает арифметический квадратный корень из числа
обозначает арифметический квадратный корень из числа 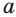 , т. е. такое неотрицательное число, квадрат которого равен
, т. е. такое неотрицательное число, квадрат которого равен 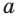 .
.
Рассмотрим уравнение
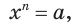
где 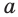 — некоторое действительное число,
— некоторое действительное число, 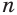 — натуральное число. Корень этого уравнения называют корнем
— натуральное число. Корень этого уравнения называют корнем 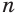 -й степени из числа
-й степени из числа 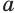 .
.
Корнем 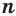 -й степени из числа
-й степени из числа 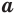 называется такое число,
называется такое число, 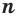 -я степень которого равна
-я степень которого равна 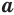 .
.
Теоремы и доказательства
Теорема 1.
Из положительного числа существует единственный положительный корень степени 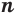 .
.
Доказательство:
Пусть 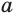 — положительное число. Нужно доказать, что существует такое единственное положительное число
— положительное число. Нужно доказать, что существует такое единственное положительное число 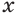 , что
, что
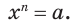
Доказательство существования искомого числа 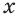 выходит за пределы тех возможностей, которые теперь у нас есть. Покажем на примере, как можно найти приближенное значение положительного корня
выходит за пределы тех возможностей, которые теперь у нас есть. Покажем на примере, как можно найти приближенное значение положительного корня 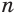 -й степени из положительного числа с любой степенью точности.
-й степени из положительного числа с любой степенью точности.
Пусть нужно найти значение корня третьей степени из числа 6. Приближенными значениями этого корня с точностью до единицы являются число 1 с недостатком и число 2 с избытком, так как
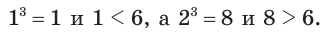
Чтобы найти нужное значение с точностью до десятой, следует испытать числа
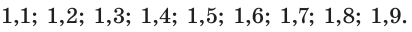
Поскольку
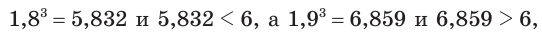
то нужное значение находится между числами 1,8 и 1,9. Испытав числа
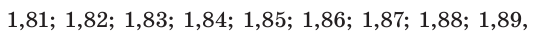
найдем, что значение корня третьей степени из числа 3 находится между числами 1,81 и 1,82.
Если этот процесс продолжать далее, то мы будем получать искомое значение корня с все большей точностью.
Докажем единственность положительного корня степени 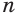 из положительного числа
из положительного числа  . Пусть есть два таких положительных числа
. Пусть есть два таких положительных числа 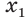 и
и 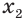 , что
, что 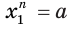 и
и 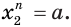 Тогда
Тогда 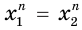 .
.
Допустим, что 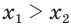 , тогда по соответствующему свойству числовых неравенств получим, что
, тогда по соответствующему свойству числовых неравенств получим, что 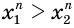 , а это противоречит отношению
, а это противоречит отношению 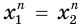 .
.
Также ведет к противоречию и допущение о том, что 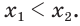
Поэтому для 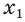 и
и 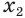 остается единственная возможность:
остается единственная возможность: 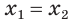 .
.
Неотрицательный корень 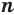 -й степени из неотрицательного числа называют арифметическим корнем
-й степени из неотрицательного числа называют арифметическим корнем 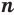 -й степени.
-й степени.
Корень 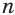 -й степени из числа
-й степени из числа 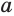 обозначают
обозначают 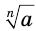 . Число
. Число 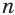 называют показателем корня, число
называют показателем корня, число 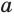 — подкоренным выражением. Если подкоренное выражение
— подкоренным выражением. Если подкоренное выражение 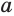 неотрицательно, то
неотрицательно, то 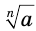 обозначает арифметический корень.
обозначает арифметический корень.
Действие нахождения корня 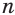 -й степени из числа
-й степени из числа 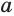 называется извлечением корня степени
называется извлечением корня степени 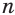 . Это действие является обратным для действия возведения в натуральную степень
. Это действие является обратным для действия возведения в натуральную степень 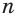 (рис. 49). Корень второй степени называют еще квадратным корнем, корень третьей степени — кубическим корнем.
(рис. 49). Корень второй степени называют еще квадратным корнем, корень третьей степени — кубическим корнем.
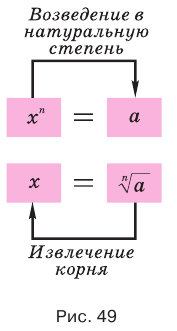
Пример №1
а) Запись 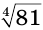 означает корень четвертой степени из числа 81.
означает корень четвертой степени из числа 81.
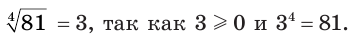
б) Запись 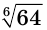 означает корень шестой степени из числа 64.
означает корень шестой степени из числа 64.
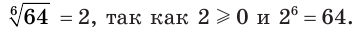
в) Запись 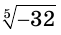 означает корень пятой степени из числа -32.
означает корень пятой степени из числа -32.
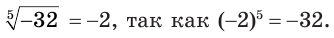
г) 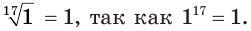
д) 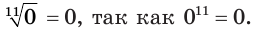
Теорема 2.
Из положительного числа:
- а) не существует отрицательного корня нечетной степени;
- б) существует единственный отрицательный корень четной степени, причем он противоположен положительному корню из данного числа.
Доказательство:
Пусть 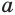 — положительное число.
— положительное число.
Пусть степень 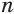 корня — нечетное число. Допустим, что есть такое отрицательное число
корня — нечетное число. Допустим, что есть такое отрицательное число 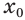 , для которого истинно равенство
, для которого истинно равенство 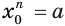 . Поскольку по условию
. Поскольку по условию 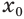 — отрицательное число, то число
— отрицательное число, то число 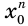 также отрицательное как произведение нечетного количества отрицательных чисел. Получается, что левый компонент
также отрицательное как произведение нечетного количества отрицательных чисел. Получается, что левый компонент 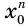 равенства
равенства 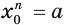 — отрицательное число, а его правый компонент
— отрицательное число, а его правый компонент 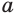 — положительное число. Но такое невозможно. Поэтому допущение о существовании отрицательного корня нечетной степени из положительного числа нужно отклонить и признать, что отрицательного корня нечетной степени из положительного числа не существует.
— положительное число. Но такое невозможно. Поэтому допущение о существовании отрицательного корня нечетной степени из положительного числа нужно отклонить и признать, что отрицательного корня нечетной степени из положительного числа не существует.
Пусть степень 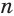 корня — четное число. По теореме 1 существует единственный положительный корень
корня — четное число. По теореме 1 существует единственный положительный корень 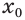 уравнения
уравнения 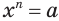 . А если истинно равенство
. А если истинно равенство 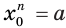 , то истинно и равенство
, то истинно и равенство 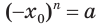 . А это означает, что
. А это означает, что 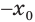 — отрицательный корень уравнения
— отрицательный корень уравнения 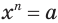 . Единственность отрицательного корня устанавливается так же, как и единственность положительного корня.
. Единственность отрицательного корня устанавливается так же, как и единственность положительного корня.
Теорема 3.
Из отрицательного числа:
- а) не существует корней четной степени;
- б) существует единственный корень нечетной степени, причем это отрицательное число.
Доказательство:
Пусть 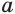 — отрицательное число.
— отрицательное число.
Пусть степень 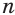 корня — четное число. Допустим, что есть такое число
корня — четное число. Допустим, что есть такое число 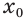 , для которого истинно равенство
, для которого истинно равенство 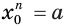 . Тогда число
. Тогда число 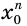 неотрицательно как произведение четного количества равных чисел
неотрицательно как произведение четного количества равных чисел 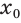 . Получается, что левый компонент
. Получается, что левый компонент 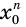 равенства
равенства 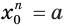 — неотрицательное число, а его правый компонент
— неотрицательное число, а его правый компонент 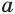 — отрицательное число. Получили противоречие. Поэтому допущение о существовании корня четной степени из отрицательного числа нужно отклонить и признать, что не существует корней четной степени из отрицательного числа.
— отрицательное число. Получили противоречие. Поэтому допущение о существовании корня четной степени из отрицательного числа нужно отклонить и признать, что не существует корней четной степени из отрицательного числа.
Пусть степень 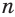 корня — нечетное число. Тогда корень
корня — нечетное число. Тогда корень 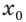 степени
степени 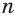 из отрицательного числа
из отрицательного числа 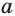 не может быть неотрицательным, так как в противном случае в равенстве
не может быть неотрицательным, так как в противном случае в равенстве 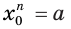 левый компонент
левый компонент 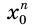 был бы неотрицательным, а правый компонент
был бы неотрицательным, а правый компонент 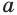 отрицательным.
отрицательным.
Поскольку 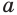 — число отрицательное, то противоположное число
— число отрицательное, то противоположное число 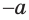 положительное. В соответствии с теоремой 1 существует положительный корень
положительное. В соответствии с теоремой 1 существует положительный корень 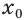 уравнения
уравнения 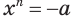 , т. е. истинно равенство
, т. е. истинно равенство 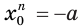 . Тогда
. Тогда 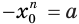 . Поскольку по условию число
. Поскольку по условию число 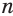 нечетное, то
нечетное, то 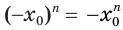 . Значит,
. Значит, 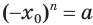 . А это и означает, что отрицательное число
. А это и означает, что отрицательное число 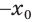 есть корень нечетной степени
есть корень нечетной степени 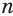 из отрицательного числа
из отрицательного числа 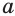 .
.
Единственность отрицательного корня нечетной степени из отрицательного числа устанавливается так же, как и единственность положительного корня.
Таким образом, если  , то выражение
, то выражение 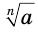 имеет значение при любом натуральном значении
имеет значение при любом натуральном значении 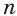 , как четном, так и нечетном, а если
, как четном, так и нечетном, а если 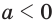 , то выражение
, то выражение 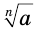 имеет значение только при нечетном натуральном значении
имеет значение только при нечетном натуральном значении 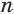 .
.
По определению корня, при каждом значении 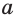 , при котором выражение
, при котором выражение 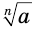 имеет значение, истинно равенство
имеет значение, истинно равенство
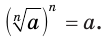
Следствие 1.
Корни нечетной степени 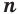 из противоположных чисел являются противоположными числами:
из противоположных чисел являются противоположными числами:
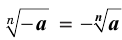 , если
, если 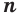 — нечетное число.
— нечетное число.
Действительно, если 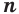 — нечетное число, то истинное равенство
— нечетное число, то истинное равенство 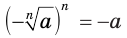 означает, что число
означает, что число 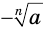 является значением корня степени
является значением корня степени 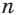 из числа
из числа 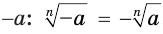 .
.
Следствие 2.
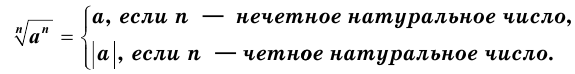
Рассмотрим примеры решения уравнений вида 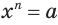 .
.
Пример №2
Решим уравнение 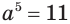 .
.
Уравнение имеет единственный корень. Он является положительным числом, пятая степень которого равна 11, т. е. числом 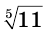 .
.
Число 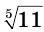 иррациональное. С помощью калькулятора находим, что с точностью до тысячной оно равно 1,615.
иррациональное. С помощью калькулятора находим, что с точностью до тысячной оно равно 1,615.
Пример №3
Решим уравнение 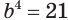 .
.
Уравнение имеет два корня, которые являются противоположными числами. Положительный корень — это положительное число, четвертая степень которого равна 21, т. е. число 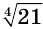 . Отрицательный корень — число
. Отрицательный корень — число 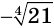 .
.
Числа 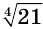 и
и 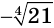 иррациональные. С помощью калькулятора находим, что с точностью до десятитысячной они равны 2,1407 и -2,1407.
иррациональные. С помощью калькулятора находим, что с точностью до десятитысячной они равны 2,1407 и -2,1407.
Пример №4
Решим уравнение 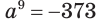 .
.
Уравнение имеет единственный корень. Он является отрицательным числом, девятая степень которого равна -373, т. е. числом 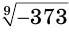 , или, используя представление с помощью арифметического корня, числом
, или, используя представление с помощью арифметического корня, числом 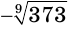 .
.
Число 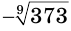 иррациональное. Его десятичное приближение с точностью до десятитысячной равно -1,9308.
иррациональное. Его десятичное приближение с точностью до десятитысячной равно -1,9308.
Свойства арифметического корня
Мы знаем, что квадратный корень имеет такие свойства:
- если
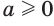 и
и 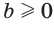 , то
, то 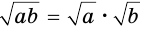 ;
; - если
 и
и 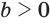 , то
, то 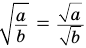 ;
; - если
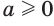 и
и 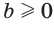 , то неравенство
, то неравенство 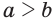 равносильно неравенству
равносильно неравенству 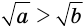 .
.
Аналогичные свойства имеет корень 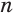 -й степени и при
-й степени и при 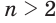 .
.
Теорема 4.
При любом натуральном значении 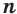 :
:
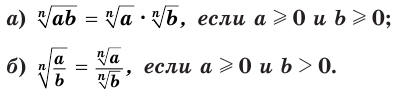
Доказательство:
Пусть  и
и 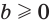 . Докажем, что
. Докажем, что 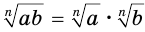 . Для этого в соответствии с определением арифметического корня нужно доказать, что:
. Для этого в соответствии с определением арифметического корня нужно доказать, что:
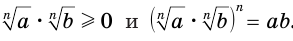
Поскольку  , то выражение
, то выражение 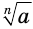 имеет значение и это значение неотрицательно. Так же поскольку
имеет значение и это значение неотрицательно. Так же поскольку 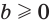 , то выражение имеет неотрицательное значение. Поэтому и выражение
, то выражение имеет неотрицательное значение. Поэтому и выражение 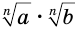 имеет неотрицательное значение.
имеет неотрицательное значение.
Далее по свойству натуральной степени произведения и определению корня получим
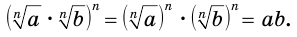
Доказательство равенства 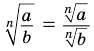 проводится аналогично.
проводится аналогично.
Следствие 1.
При любом нечетном натуральном значении 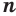 :
:
- а)
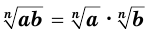 , если
, если 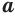 и
и 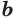 — любые числа;
— любые числа; - б)
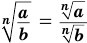 , если
, если 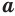 — любое число и
— любое число и 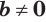 .
.
Действительно, если, например,  и
и 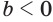 , то
, то 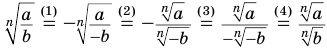 . Здесь использованы (1) и (4) — следствие 1 из параграфа 3, (2) — теорема 4, (3) — свойство дроби.
. Здесь использованы (1) и (4) — следствие 1 из параграфа 3, (2) — теорема 4, (3) — свойство дроби.
Теорема 4 дает правила извлечения корня из произведения и из дроби:
- чтобы найти корень из произведения, можно найти корни из отдельных множителей и полученные числа перемножить;
- чтобы извлечь корень из дроби, можно извлечь его отдельно из числителя и знаменателя и первый результат разделить на второй.
Прочтение тождеств из теоремы 4 справа налево:
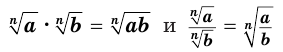
дает правила умножения и деления корней с одинаковыми показателями:
- чтобы перемножить корни с одинаковыми показателями, можно перемножить их подкоренные выражения и извлечь корень из полученного произведения.
- чтобы разделить корни с одинаковыми показателями, можно разделить их подкоренные выражения и извлечь корень из полученного частного.
Пример №5
а) 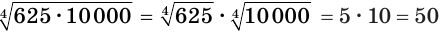 ;
;
б) 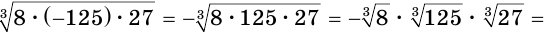
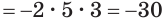 ;
;
в) 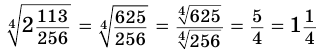 ;
;
г) 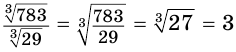 .
.
Теорема 5.
Если 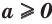 , то при любых натуральных значениях
, то при любых натуральных значениях 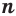 и
и 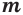 истинны равенства
истинны равенства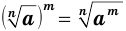 и
и 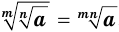 .
.
Доказательство:
Пусть 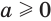 . Тогда:
. Тогда:
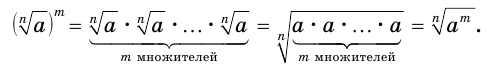
Докажем второе тождество. Выражение 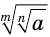 имеет значение, причем это значение неотрицательно. Поскольку
имеет значение, причем это значение неотрицательно. Поскольку
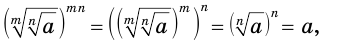
то выражение 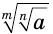 является значением корня степени
является значением корня степени 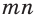 из числа
из числа 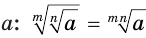 .
.
Следствие 2.
Если 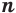 и
и 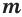 — нечетные числа, то при любом значении
— нечетные числа, то при любом значении 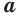 истинны равенства
истинны равенства 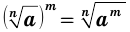 и
и 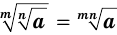 .
.
Действительно, если, например,  ,
, 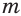 и
и 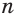 — нечетные числа, то
— нечетные числа, то
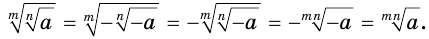
Теорема 5 позволяет сформулировать правило возведения корня в степень и правило извлечения корня из корня:
- чтобы возвести корень в степень, можно возвести в эту степень подкоренное выражение, оставив показатель корня прежним;
- чтобы извлечь корень из корня, можно перемножить показатели корней, оставив подкоренное выражение без изменений.
Пример №6
a) 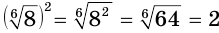 ;
;
б) 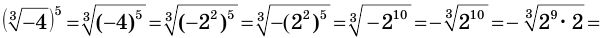
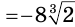 ;
;
в) 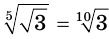 .
.
Следствие 3.
Если  , то при любых натуральных значениях
, то при любых натуральных значениях  ,
, 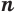 и
и 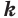 истинно равенство
истинно равенство 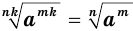 .
.
Действительно:
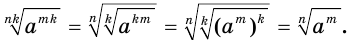
Доказанное утверждение выражает основное свойство корня:
- если показатель корня и показатель подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
Пример №7
а) 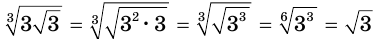 ;
;
б) 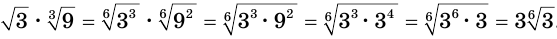
Можно доказать, что если  ,
, 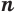 и
и 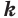 — нечетные числа, то при всех значениях
— нечетные числа, то при всех значениях 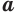 истинно равенство
истинно равенство 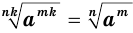 .
.
Теорема 6.
Если 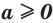 и
и 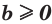 , то неравенство
, то неравенство 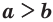 равносильно неравенству
равносильно неравенству 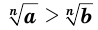 при любом натуральном значении
при любом натуральном значении 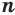 .
.
Доказательство:
Пусть 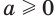 и
и 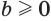 . Тогда выражения
. Тогда выражения 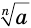 и
и 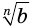 имеют значения при любом значении
имеют значения при любом значении 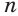 .
.
Пусть 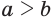 . Допустим, что
. Допустим, что 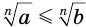 . Возведя обе части этого неравенства с неотрицательными компонентами в
. Возведя обе части этого неравенства с неотрицательными компонентами в 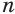 -ю степень, получим
-ю степень, получим 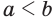 . Но это противоречит условию
. Но это противоречит условию 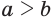 .
.
Пусть 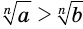 . Возведя обе части этого неравенства с неотрицательными компонентами в
. Возведя обе части этого неравенства с неотрицательными компонентами в 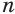 -ю степень, получим
-ю степень, получим 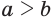 .
.
Следствие 4.
Если 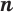 — нечетное число, то неравенство
— нечетное число, то неравенство 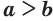 равносильно неравенству
равносильно неравенству 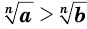 при любых значениях
при любых значениях 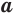 и
и 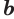 .
.
Действительно, если 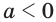 и
и 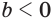 , то
, то 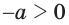 и
и 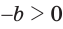 . Неравенство
. Неравенство 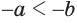 по уже доказанному равносильно неравенству
по уже доказанному равносильно неравенству 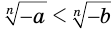 , или неравенству
, или неравенству 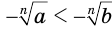 , или неравенству
, или неравенству 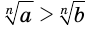 . Получили, что если
. Получили, что если 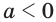 и
и 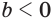 , то неравенство
, то неравенство 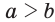 равносильно неравенству
равносильно неравенству 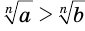 .
.
Равносильность неравенств в случаях, когда числа 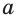 и
и 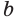 имеют разные знаки и когда одно из чисел равно нулю, устанавливается аналогично.
имеют разные знаки и когда одно из чисел равно нулю, устанавливается аналогично.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |