Координаты на плоскости - определение и вычисление с примерами решения

Координаты на плоскости:

Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке

Определение: Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) направления, 2) масштаб и 3) общая точка отсчета.

Назовем одну из осей осью или осью абсцисс, другую—осью или осью ординат. Точку их пересечения назовем началом координат.

Возьмем произвольную точку 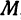, лежащую на плоскости, и опустим из нее перпендикуляры на оси координат, т. е. найдем ее проекции на оси. Обозначим проекцию на ось 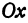через 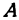, а проекцию на ось 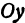через 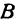. Обозначим координату точки 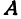(по оси 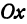) через 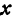, а координату точки 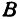(по оси 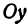) через 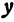. Введем определение:

Определение. Абсциссой точки называется координата ее проекции на ось 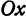. Ординатой точки называется координата ее проекции на ось .

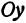Абсциссу точки обычно обозначают буквой 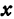, ординату— буквой 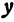. Точку 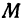, имеющую абсциссу 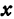и ординату 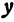, обозначают следующим образом: пишут скобку и в ней на первом месте ставят абсциссу, на втором ординату и разделяют эти два числа запятой или точкой с запятой. Таким образом, запись точки выглядит так: .

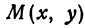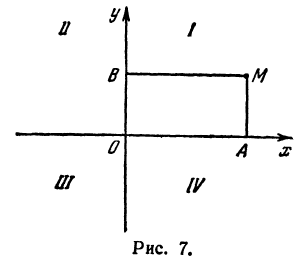
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.

Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.

Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.

Третьей четвертью—та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой,—та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7). На рис. 8 указаны 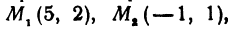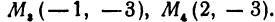Заметим, что абсцисса 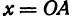по абсолютной величине равна расстоянию точки от оси ординат, так как 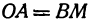(см. рис. 7), а ордината — расстоянию точки 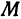от оси абсцисс, так как .

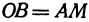Пример:

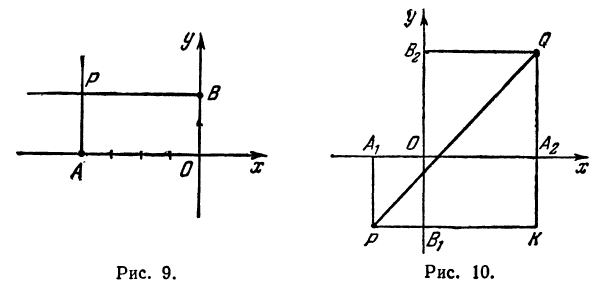
Найти точку 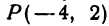(рис. 9).

Решение:

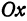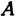Возьмем на оси точку с координатой 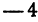, ее координатный отрезок 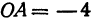. На оси 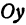возьмем точку 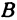с координатным отрезком 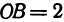. Восставим перпендикуляры к осям из точек 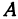и 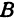, точка их пересечения и даст искомую точку .

Пример:

Найти расстояние между точкам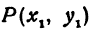и и 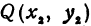. Иначе говоря, нужно найти длину отрезка 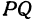(рис. 10).

Решение:

Обозначим проекцию точки 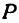на ось 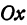через 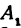, а ее проекцию на ось 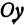— через 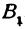. Проекцию точки 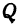на ось 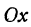обозначим через 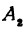и через 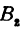— ее проекцию на ось 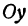. Тогда 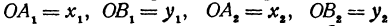. Из точки 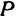проведем прямую, параллельную оси 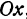, до пересечения с прямой 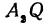в точке 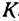. Рассмотрим треугольник 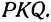По теореме Пифагора имеем 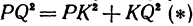. to 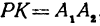, , 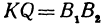как противоположные стороны прямоугольников; кроме того, на основании формулы (3 из § 1) направленные отрезк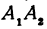и , и 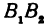будут равны 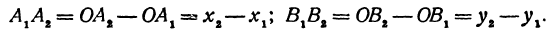Подставляя полученные выражения в 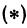, получим

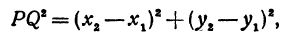
откуда

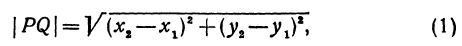
т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей, координат.

Примечание. Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.

Пример:

Найти расстояние между точкам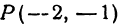и и .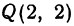

Решение:

Применяя формулу (1), получим

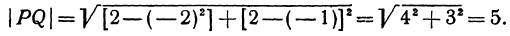
Пример:

Найти длину отрезка 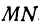, если даны 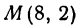и .

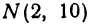Решение:

Применяя формулу (1), получим

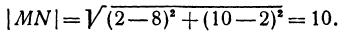
Пример:

Найти точку 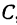, делящую отрезок 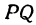в отношении 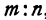, если известны координаты точек 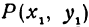и .

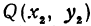Решение:

По условию задачи надо найти такую точку 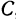, чтобы было выполнено равенство

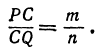
Обозначим, как и выше, проекции точки 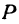на оси через 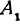и 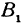, а проекции точки 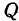—через 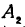и 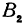; тогда 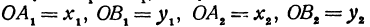(рис. 11).

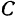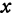Кроме того, обозначим координаты искомой точки через и 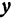, а ее проекции на оси — через 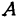и 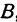, т. е.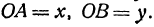

Так как прямые 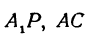и 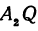параллельны между собой, то на основании теоремы о пропорциональных отрезках можно записать, что

Но 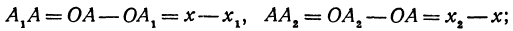поэтому, подставляя в равенство 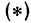, будем иметь уравнение

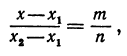
решая которое найдем абсциссу точки :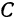

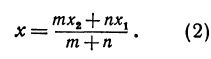
Рассуждая аналогично о проекциях на оси 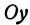, т.е. о точках 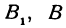и 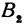, по- лучим ординату точки 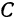, делящей отрезок в отношении ,

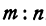Итак, искомая точка 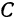имеет координаты, определяемые равенствами (2) и (3).

Пример:

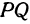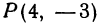Найти точку, делящую в отношении 1:2 отрезок , где и .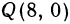

Здесь .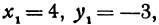

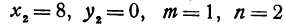Решение:

Применяя формулы (2) и (3), получим:

• Заказать решение задач по высшей математике

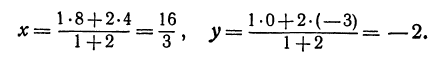
Пример:

Найти точку, делящую расстояние между точкам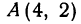и и 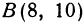в отношении 3:1.

Здесь .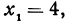

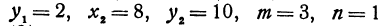Решение:

По формулам (2) и (3) находим:

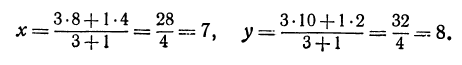
Следствие (из формул (2) и (3)). Если точка 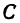делит отрезок 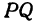пополам, то 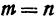, поэтому

т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.

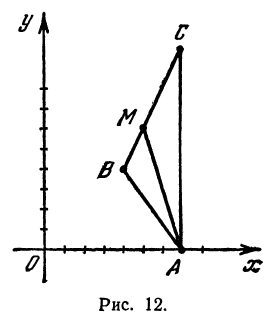
Пример:

Даны три вершины треугольника: 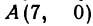, 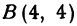и 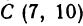. Найти длину биссектрисы угла 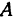(рис. 12).

Решение:

Найдем длины сторон 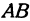и 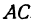. Для этого применим формулу (1):

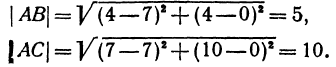
Обозначим точку пересечения биссектрисы угла с противоположной стороной через , а ее координаты—через 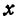и 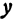. Помня, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, можно утверждать, что точка 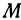делит отрезок 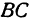в отношении 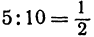; поэтому, применяя формулы (2) и (3), получим:

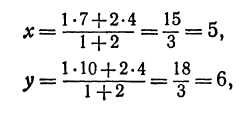
т.е. (5,6).

Теперь вычисляем длину биссектрисы как расстояние между точкам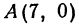и и :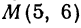

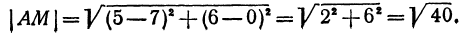
Пример:

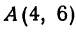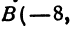
Найти точку пересечения медиан треугольника, вершинами которого являются точки , (рис. 13).

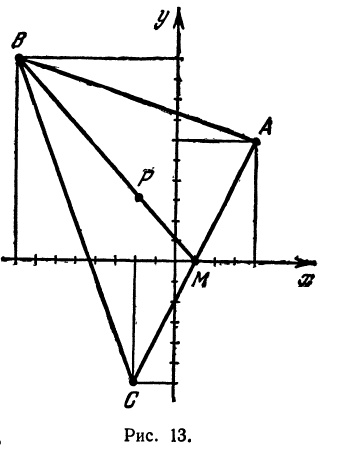
Решение:

Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через 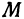середину стороны 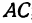; по формулам (4) и (5) можно найти ее координаты:

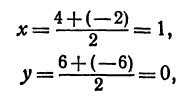
т. е. 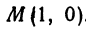. Точка 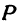пересечения медиан делит отрезок 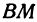в отношении 2:1, поэтому ее координаты найдутся по формулам (2) и (3):

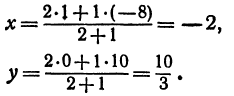
Итак, искомая точка 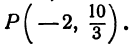Задача 5. Записать условие того, что точка 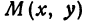находится на расстоянии 5 от точки 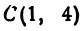. По формуле (1) имеем

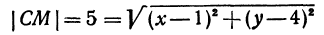
или, возводя обе части равенства в квадрат, получим

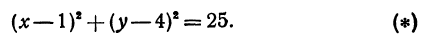
Это равенство есть уравнение с двумя неизвестным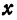и и 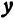. Этому уравнению удовлетворяют координаты любой точки, лежащей на расстоянии 5 от точки 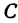. Иначе говоря, ему удовлетворяют координаты любой точки, принадлежащей геометрическому месту точек, расстояние которых от точки 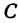равно 5. Это геометрическое место есть окружность.

Следовательно, можно сказать, что уравнение 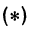есть уравнение окружности с центром в точке 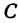и радиуса 5.

В следующих главах будут рассмотрены уравнения с двумя неизвестным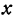и и 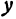и те линии (геометрические места), точки которых имеют координаты, удовлетворяющие этим уравнениям.