
Конус в геометрии - элементы, формулы, свойства с примерами
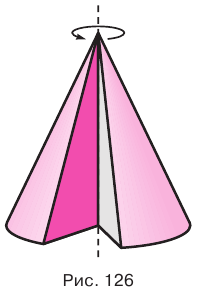
Конусом называется тело, полученное вращением прямоугольного треугольника вокруг оси, проходящей через один из его катетов (рис. 126).
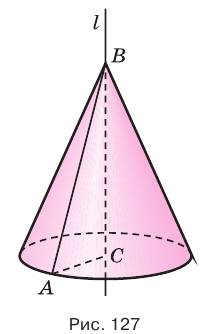
На рисунке 127 показано образование конуса при вращении прямоугольного треугольника 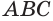 вокруг прямой
вокруг прямой 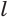 , которой принадлежит катет
, которой принадлежит катет 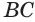 . При этом ломаная
. При этом ломаная 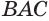 описывает поверхность конуса, гипотенуза
описывает поверхность конуса, гипотенуза 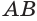 — боковую поверхность, а катет
— боковую поверхность, а катет 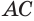 — основание конуса (рис. 128). Саму гипотенузу
— основание конуса (рис. 128). Саму гипотенузу 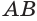 называют образующей конуса, неподвижную точку
называют образующей конуса, неподвижную точку 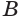 — вершиной конуса, прямую, проходящую через неподвижный катет
— вершиной конуса, прямую, проходящую через неподвижный катет 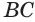 , — осью конуса, а перпендикуляр, опущенный из вершины конуса на основание, — высотой конуса (рис. 129). Основание высоты конуса совпадает с центром основания конуса.
, — осью конуса, а перпендикуляр, опущенный из вершины конуса на основание, — высотой конуса (рис. 129). Основание высоты конуса совпадает с центром основания конуса.
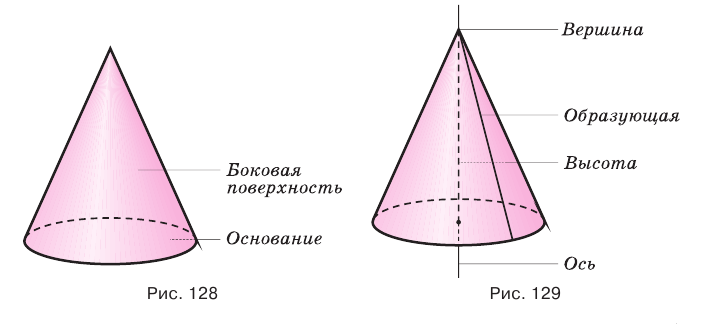
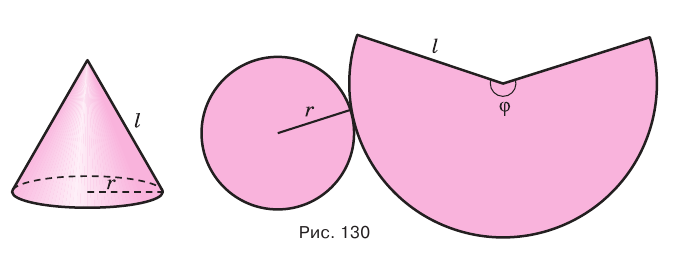
Поверхность конуса можно развернуть на плоскость, в результате получится сектор, представляющий боковую поверхность конуса, и круг, представляющий основание конуса. На рисунке 130 представлены конус и его развертка.
Теорема 5.
Боковая поверхность конуса равна произведению полуокружности его основания и образующей:
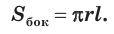
Доказательство проведите самостоятельно, используя рисунок 130.
Важной пространственной конфигурацией, которая часто встречается в задачах, является сочетание конуса с плоскостью.
Если конус пересечь плоскостью, параллельной основанию, то получится круг (рис. 131), а если плоскостью, проходящей через вершину, то — равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 132).
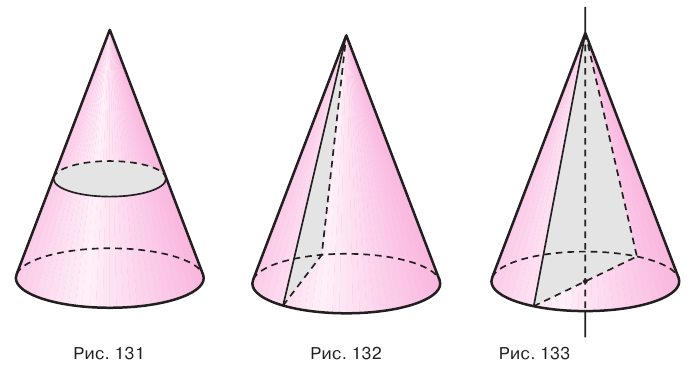
Осевое сечение конуса, т. е. сечение плоскостью, проходящей через ось конуса, является равнобедренным треугольником, у которого основание равно диаметру основания конуса (рис. 133).
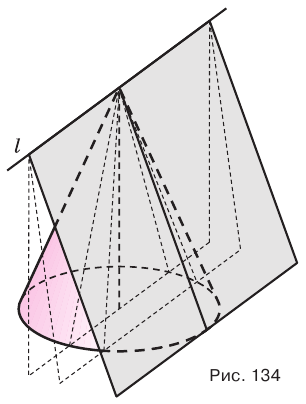
Проведем через вершину конуса секущую плоскость и будем ее поворачивать вокруг прямой, перпендикулярной оси конуса (рис. 134). При этом основание треугольника-сечения будет укорачиваться, а его боковые стороны сближаться до того момента, пока не совпадут. Получим плоскость, целиком содержащую образующую и не имеющую с конусом других общих точек. Такая плоскость называется касательной плоскостью конуса.
Теорема 6.
Если плоскость касается конуса по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось конуса.
Доказательство:
Пусть плоскость 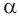 касается конуса с осью
касается конуса с осью  по образующей
по образующей 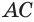 (рис. 135). Докажем, что плоскость, содержащая эту образующую и ось
(рис. 135). Докажем, что плоскость, содержащая эту образующую и ось  , перпендикулярна плоскости
, перпендикулярна плоскости 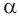 .
.
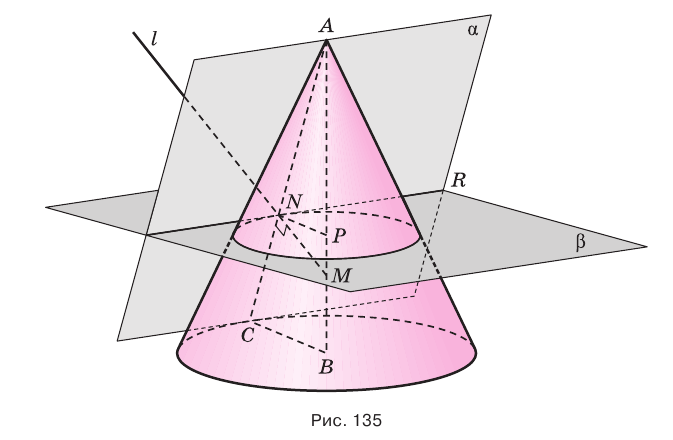
Проведем прямую 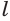 , которая перпендикулярна образующей
, которая перпендикулярна образующей  , пересекает ось конуса в точке
, пересекает ось конуса в точке 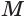 , отличной от вершины
, отличной от вершины 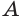 . Через точку
. Через точку 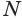 проведем плоскость
проведем плоскость 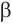 , перпендикулярную оси
, перпендикулярную оси  , она пересечет конус по кругу с центром
, она пересечет конус по кругу с центром 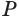 и плоскость
и плоскость 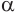 — по прямой
— по прямой 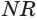 , касающейся окружности с центром
, касающейся окружности с центром 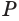 . Эта касательная по свойству касательной к окружности перпендикулярна радиусу
. Эта касательная по свойству касательной к окружности перпендикулярна радиусу 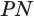 соответствующей окружности. Но этот радиус является проекцией наклонной
соответствующей окружности. Но этот радиус является проекцией наклонной 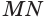 на плоскость
на плоскость 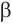 , поэтому по теореме о трех перпендикулярах прямая
, поэтому по теореме о трех перпендикулярах прямая 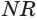 перпендикулярна наклонной
перпендикулярна наклонной 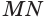 , т. е. прямой
, т. е. прямой 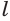 .
.
Таким образом, прямая 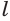 перпендикулярна прямым
перпендикулярна прямым  и
и 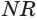 , которые пересекаются и лежат в плоскости
, которые пересекаются и лежат в плоскости 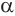 , поэтому по признаку перпендикулярности прямой и плоскости прямая
, поэтому по признаку перпендикулярности прямой и плоскости прямая 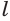 перпендикулярна плоскости
перпендикулярна плоскости  . Значит, плоскость
. Значит, плоскость 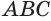 , содержащая прямую
, содержащая прямую  , перпендикулярна плоскости
, перпендикулярна плоскости  .
.
Теорема 6 выражает свойство касательной плоскости конуса.
Теорема 7.
Плоскость касается конуса, если она проходит через его образующую и перпендикулярна плоскости, проходящей через эту образующую и ось конуса.
Доказательство:
Пусть плоскость  проходит через образующую
проходит через образующую  конуса с осью
конуса с осью  и перпендикулярна плоскости
и перпендикулярна плоскости  (рис. 136). Докажем, что плоскость
(рис. 136). Докажем, что плоскость  касается конуса, т. е. что точки образующей
касается конуса, т. е. что точки образующей  , и только они, являются общими точками конуса и плоскости
, и только они, являются общими точками конуса и плоскости  .
.
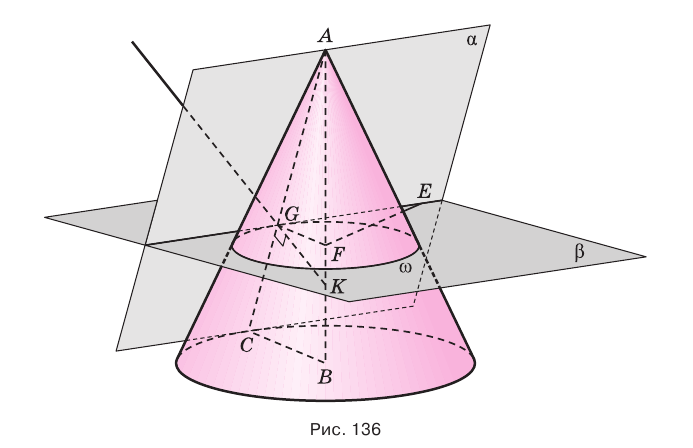
Точки образующей  принадлежат и конусу, и плоскости
принадлежат и конусу, и плоскости  . Пусть
. Пусть  — какая-либо точка плоскости
— какая-либо точка плоскости  вне образующей
вне образующей  . Через эту точку проведем плоскость
. Через эту точку проведем плоскость 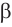 , перпендикулярную оси
, перпендикулярную оси  , она пересекает поверхность конуса по окружности
, она пересекает поверхность конуса по окружности 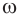 с центром
с центром 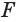 , образующую
, образующую  — в некоторой точке
— в некоторой точке 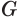 и плоскость
и плоскость  — по прямой
— по прямой 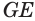 . Пусть
. Пусть 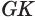 — прямая, которая перпендикулярна плоскости
— прямая, которая перпендикулярна плоскости  и пересекает ось
и пересекает ось  в точке
в точке 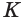 . Тогда по теореме о трех перпендикулярах прямая
. Тогда по теореме о трех перпендикулярах прямая 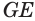 , проведенная в плоскости
, проведенная в плоскости 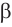 через основание наклонной
через основание наклонной 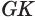 перпендикулярно к ней, перпендикулярна ее проекции
перпендикулярно к ней, перпендикулярна ее проекции 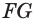 . Значит,
. Значит, 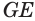 — касательная к окружности
— касательная к окружности 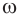 , и поэтому точка
, и поэтому точка 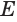 находится вне окружности
находится вне окружности 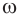 , а значит, и вне конуса.
, а значит, и вне конуса.
Теорема 7 выражает признак касательной плоскости конуса.
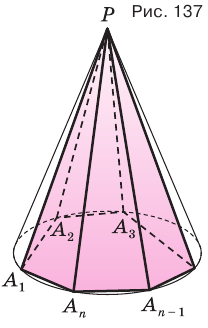
Пусть есть конус с вершиной 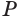 (рис. 137). Впишем в основание конуса многоугольник
(рис. 137). Впишем в основание конуса многоугольник 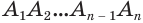 и через его вершины
и через его вершины 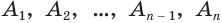 проведем образующие
проведем образующие 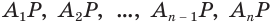 . В результате получим тело
. В результате получим тело 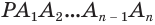 , являющееся пирамидой. Ее называют пирамидой, вписанной в конус, а сам конус — конусом, описанным около пирамиды.
, являющееся пирамидой. Ее называют пирамидой, вписанной в конус, а сам конус — конусом, описанным около пирамиды.
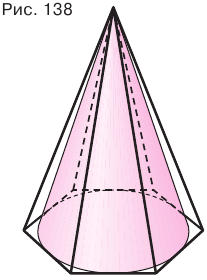
Если основание конуса вписано в основание пирамиды, а боковая поверхность конуса касается боковых граней пирамиды, то говорят, что пирамида описана около конуса, или конус вписан в пирамиду (рис. 138).
Теорема 8.
Объем конуса равен третьей доле произведения площади Рис. 139 т его основания и высоты:
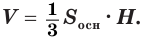
Доказательство:
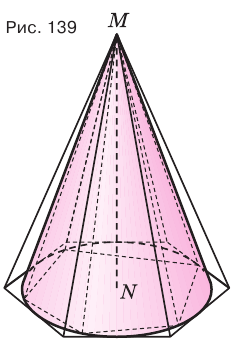
Пусть есть конус с осью 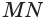 (рис. 139). В него впишем правильную пирамиду
(рис. 139). В него впишем правильную пирамиду 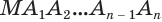 , а около него опишем правильную пи-рамиду
, а около него опишем правильную пи-рамиду 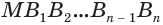 . В соответствии с теоремой 4 объем первой пирамиды равен третьей доле произведения площади многоугольника
. В соответствии с теоремой 4 объем первой пирамиды равен третьей доле произведения площади многоугольника 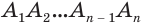 и высоты
и высоты 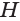 пирамиды, т. е. высоты конуса, а объем второй — произведению площади многоугольника
пирамиды, т. е. высоты конуса, а объем второй — произведению площади многоугольника 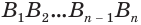 и той же высоты. Объем самого конуса заключен между этими числами.
и той же высоты. Объем самого конуса заключен между этими числами.
Будем увеличивать количество 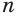 сторон оснований пирамид. Тогда объем первой пирамиды будет увеличиваться, объем второй — уменьшаться, причем их разность стремится к нулю, если значение переменной
сторон оснований пирамид. Тогда объем первой пирамиды будет увеличиваться, объем второй — уменьшаться, причем их разность стремится к нулю, если значение переменной 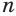 неограниченно увеличивается. То число, к которому приближаются объемы обеих пирамид, принимается за объем конуса.
неограниченно увеличивается. То число, к которому приближаются объемы обеих пирамид, принимается за объем конуса.
В описанном процессе высота 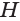 пирамиды не изменяется, а площади обоих многоугольников —
пирамиды не изменяется, а площади обоих многоугольников — 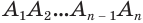 и
и 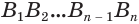 — стремятся к площади
— стремятся к площади 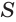 круга, являющегося основанием конуса. Значит, объем
круга, являющегося основанием конуса. Значит, объем 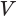 конуса равен третьей доле произведения площади
конуса равен третьей доле произведения площади 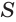 основания конуса и его высоты
основания конуса и его высоты 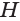 :
:
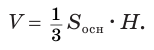
Теорема 9.
Если конус пересечь плоскостью, параллельной его основанию, то:
- а) образующая и высота разделяются на пропорциональные части;
- б) площади сечения и основания относятся как квадраты их расстояний от вершины.
Используя рисунок 140, докажите эту теорему самостоятельно.
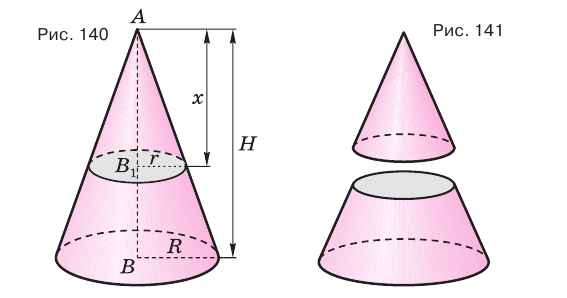
Секущая плоскость, параллельная основанию конуса, разделяет его на две части (рис. 141). Одна из этих частей также является конусом, а другая — телом, которое называется усеченным конусом.
Основание данного конуса и круг, полученный в сечении, называют основаниями усеченного конуса, а отрезок образующей данного конуса, заключенный между его основанием и секущей плоскостью, — образующей усеченного конуса (рис. 142). Высотой усеченного конуса называется перпендикуляр, проведенный из какой-либо точки одного его основания к плоскости другого основания.
Усеченный конус можно получить вращением прямоугольной трапеции вокруг боковой стороны, к которой прилежат прямые углы (рис. 143).

Пример:
Найдем боковую поверхность усеченного конуса. Пусть есть усеченный конус, у которого радиусы оснований 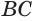 и
и 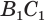 равны
равны 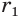 и
и 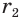 соответственно, а образующая
соответственно, а образующая 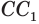 равна
равна 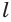 (рис. 144).
(рис. 144).
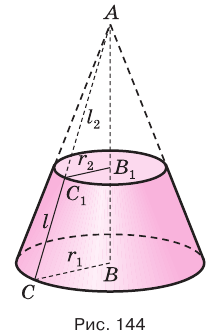
Достроим его до полного конуса. Достроенная часть представляет собой конус, у которого радиус основания равен 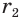 . Пусть образующая
. Пусть образующая 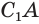 достроенного конуса равна
достроенного конуса равна 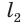 .
.
Боковую поверхность 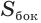 усеченного конуса можно получить как разность боковых поверхностей
усеченного конуса можно получить как разность боковых поверхностей 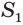 и
и 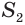 полного и достроенного конусов. Пусть
полного и достроенного конусов. Пусть 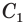 и
и 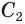 — длины окружностей нижнего и верхнего оснований усеченного конуса.
— длины окружностей нижнего и верхнего оснований усеченного конуса.
Тогда:
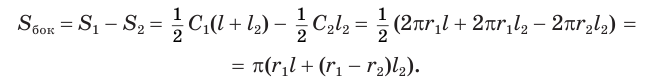
Найдем 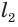 , учитывая подобие треугольников
, учитывая подобие треугольников 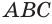 и
и 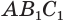 :
:
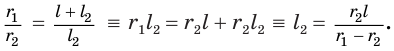
Значит,
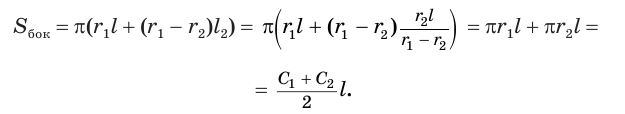
Таким образом, боковая поверхность усеченного конуса равна произведению полусуммы длин окружностей его оснований и образующей.
Пример:
Используя рисунок 144, можно, как и для усеченной пирамиды (см. параграф 9), доказать, что объем 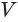 усеченного конуса равен третьей доле произведения высоты
усеченного конуса равен третьей доле произведения высоты 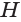 конуса и суммы площадей
конуса и суммы площадей 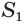 и
и 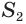 оснований конуса и их среднего геометрического
оснований конуса и их среднего геометрического 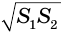 :
:
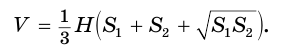
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |