
Конструктивное отображение пространства в начертательной геометрии с примерами
Содержание:
Начертательная геометрия представляет собой раздел геометрии, занимающийся изучением форм предметов реального мира и абстрактных закономерностей с использованием ’’плоских эквивалентов многомерного пространства”— чертежей.
В этой связи содержание начертательной геометрии можно свести к следующим двум основным вопросам:
- а) разработке способов построения изображений (чертежей) пространственных фигур на двумерной плоскости;
- б) изучению способов решения и исследования пространственных задач при помощи ’’плоских эквивалентов” (чертежей).
Потребность в построении изображений проявлялась уже на ранних стадиях развития человеческого общества. Об этом свидетельствуют многочисленные изображения на камнях и скалах, на предметах и орудиях первобытного человека, сохранившиеся до нашего времени. В дальнейшем развитие производственной деятельности человека поставило перед ним задачу более точного изображения пространственных предметов на плоскости. Строительство крепостных укреплений и других сооружений требовало предварительного составления их изображений или чертежей. Чертежи были необходимы и для производства механизмов и во многих других проявлениях производственной деятельности. Создалась ситуация, когда изготовление любого предмета начинается с составления его чертежей, позволяющих не только определить форму и размеры всех частей предмета, но и получать наглядное представление о нем. Ужесточающиеся требования, предъявлявшиеся к чертежам, привели к необходимости разработать «теорию изображений», которая и составляет основу начертательной геометрии.
В начертательной геометрии чертеж является инструментом, осуществляющим непосредственное изучение геометрических форм предметов и позволяющим решать пространственные задачи. Это обуславливает ряд требований, предъявленных к чертежам, наиболее существенные следующие:
- а) чертеж должен быть наглядным, т.е. он должен давать пространственное представление изображаемого предмета;
- б) он должен быть обратимым, т.е. таким, чтобы по нему можно было бы точно воспроизвести форму и размеры изображаемого предмета;
- в) чертеж должен быть достаточно простым с точки зрения его выполнения. Графические операции, выполняемые на чертеже, должны давать достаточно точные решения.
Для всех видов технических чертежей «обратимость» является особенно важным требованием. Чертеж - это производственный документ, по которому выполняется то или другое изделие. Поэтому необходимо, чтобы по чертежу можно было точно установить форму и размеры будущего изделия, а также некоторые другие данные о нем. Кроме того, чертеж дает наглядное представление об изделии, что в свою очередь облегчает его выполнение. Никакие описания предмета не могут заменить чертежа. Последний является «языком техника», как говорил один из создателей начертательной геометрии французский ученый и инженер Гаспар Монж (1746—1818).
Очевидно, что не всякое изображение предмета на плоскости позволяет точно определить его форму и положение в пространстве. Необходимо, чтобы чертеж объекта был построен по определенным правилам, позволяющим от плоских и, следовательно, искаженных форм на чертеже переходить к натуральным пространственным формам реального объекта.
Такое геометрически закономерное изображение пространственного объекта на плоскости достигается на основе метода проецирования, который является основным в начертательной геометрии. Чертежи, построенные по методу проецирования, получили название проекционных.
Следует иметь в виду, что переход от пространственных объектов, непосредственно наблюдаемых человеком, к их изображениям на плоскости (проекционным чертежам), а затем умение пользоваться такими изображениями взамен самих предметов нередко вызывают на первых порах большие трудности.
Начертательная геометрия является той научной дисциплиной, которая формализует процесс построения и реконструкции чертежей, что значительно облегчает интерпретацию изображений не только в технике, но и вообще в практической жизни человека.
Одним из направлений при изучении начертательной геометрии является моделирование соответствующих геометрических форм. Другое направление глубокая формализация методов построения и реконструкции чертежей.
На первом этапе допустимо использование первого подхода, в дальнейшем желательно базироваться на втором.
В методическом пособии приняты следующие условности и обозначения.
Рассматривается расширенное Евклидово пространство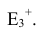
Все объекты такого пространства рассматриваются как множества точек. В качестве характеристики множества выступает его размерность. Точка представляется нульмерным множеством, линия — одномерным множеством точек, а поверхность - двумерным множеством точек (при рассмотрении каркасов поверхность представляется одномерным множеством линий).
Пособие построено на базе синтетической начертательной геометрии, в которой все элементы пространства моделируются симплексами. Симплексы объектов большей размерности конструируются на базе симплексов меньшей размерности.
В целях уменьшения объема пособия в тексте применяются широко используемые в математике обозначения операций такие, как 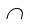
Конструктивное отображение пространства
Начертательная геометрия, являясь одним из разделов математики, изучает методы отображения пространства на плоскость и способы графических решений стереометрических задач на чертеже.
Известны три основных способа отображения пространства: конструктивный, аналитический и аксиоматический.
Начертательная геометрия базируется на конструктивном способе отображения. Это и определяет основной метод начертательной геометрии — метод проецирования.
Проецирование
В математике под проецированием понимают процесс установления однозначного соответствия между точками пространства и точками подпространств меньшей размерности.
Применительно к задачам реального мира, в конкретизированном понимании этого процесса, проецирование — это установление однозначного соответствия между точками трехмерного пространства и точками плоскости.
Один из вариантов установления такого соответствия - это проведение прямых. Аппарат проецирования, в этом случае, представляет из себя плоскость проекции или картинную плоскость П и центр проецирования S (точка, не лежащая в этой плоскости).
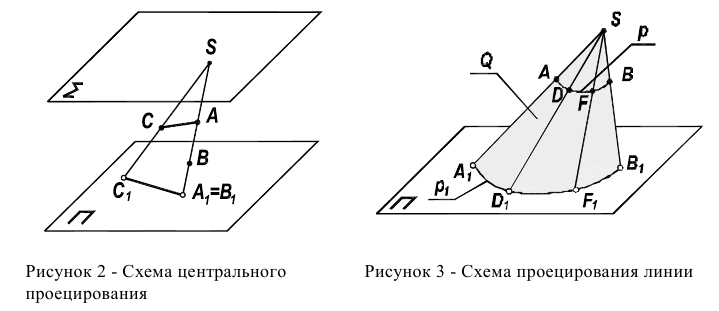
Соответствие устанавливается с помощью прямых L (рисунок 1), которые получили название проецирующих прямых или проецирующих лучей. В том случае, когда точка S - действительная точка пространства, говорят о центральном проецировании. Модель такого проецирования приведена на рисунке 2. В этой модели точке А, расположенной в пространстве, соответствует в картинной плоскости точка 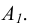 . Эта точка
. Эта точка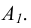 получила название проекции точки А. Проекция
получила название проекции точки А. Проекция 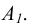 получается в результате пересечения проецирующей прямой AS с плоскостью проекции П.
получается в результате пересечения проецирующей прямой AS с плоскостью проекции П.
Для этой модели характерно следующее:
- а) точке в пространстве соответствует единственная проекция (т.к. через две точки А и S можно провести одну единственную проецирующую прямую),
- б) проекции точек, лежащих на линиях, лежат на проекциях этих линий,
- в) для точек, расположенных в плоскости
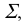 параллельной плоскости П и проходящей через точку S, нет возможности получить проекции. Также не определена проекция точки S,
параллельной плоскости П и проходящей через точку S, нет возможности получить проекции. Также не определена проекция точки S, - г) проекцией прямой в этой модели является прямая
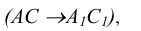
- д) проекция отрезка прямой, лежащей на проецирующей линии, -вырожденная. Концы проекций отрезка совпадают
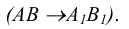
Проекцию линии можно получить, проецируя из центра S ряд точек, принадлежащих этой кривой. Полученная проекция будет единственной для данной линии при заданном положении центра S и Р. В этом случае проекция может рассматриваться как результат пересечения конической поверхности 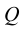 с картинной плоскостью
с картинной плоскостью 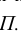
Следует отметить, что проекция линии и центр проекций не определяют положения линии в пространстве: на конической поверхности можно разместить множество линий, дающих в одну и ту же проекцию.
Центральное проецирование иначе называют коническим, т.к. проецирующими поверхностями является различного рода конусы.
Перенос центра проецирования S в бесконечность позволяет несколько улучшить модель проецирования. Вопрос о невозможности получать проекции реальных объектов отпадает.
Проецирующие прямые переходят в параллельные (такие прямые пересекаются в несобственной точке). Исходная модель переходит в модель параллельного проецирования.
Все свойства при этом сохраняются.
Вместе с этим, для этой модели, нужно отметить следующее: отрезок прямой СК, параллельной плоскости проекций 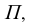 , проецируется на эту плоскость в натуральную величину (как противоположные стороны параллелограмма).
, проецируется на эту плоскость в натуральную величину (как противоположные стороны параллелограмма).
Здесь сохраняется простое отношение трех точек
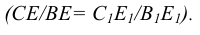
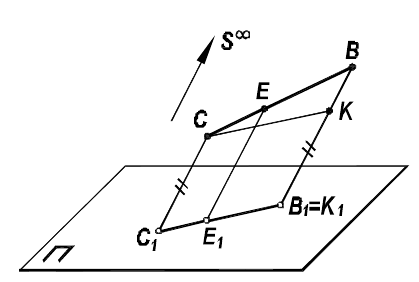
Рисунок 4 - Схема параллельного проецирования
Если в модели параллельного проецирования проецирующие прямые перпендикулярны плоскости проекций, то говорят о прямоугольном (ортогональном) проецировании, остальные случаи представляют собой косоугольное проецирование.
Для обеих рассмотренных выше моделей очевидно, что полученные с их помощью чертежи (проекции) не позволяют реконструировать форму и положение объекта в пространстве.
Такие однокартинные чертежи получили название необратимых. Рассмотрим возможность построения чертежей, допускающих реконструкцию пространственных объектов.
Моделирование трехмерного пространства
Известно несколько способов, позволяющих получать обратимые чертежи. Наиболее распространенные из них базируются на схеме метода двух изображений.
Аппарат классического метода двух изображений состоит из основного центра проецирования S, плоскости изображения 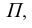 , двух вспомогательных плоскостей проекций
, двух вспомогательных плоскостей проекций 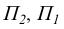 и двух вспомогательных центров проецирования
и двух вспомогательных центров проецирования  (рисунок 5).
(рисунок 5).
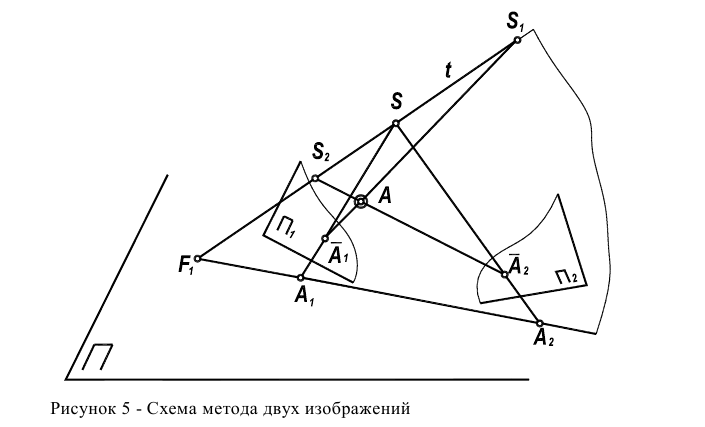
Центры проецирования  и S принадлежат одной прямой t, которая пересекает главную картинную плоскость
и S принадлежат одной прямой t, которая пересекает главную картинную плоскость  в исключенной точке
в исключенной точке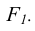 Произвольная точка А пространства изображается на чертеже двумя проекциями
Произвольная точка А пространства изображается на чертеже двумя проекциями 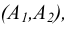 лежащими на одной прямой с точкой
лежащими на одной прямой с точкой 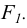
Первоначально точка А проецируется из вспомогательных центров 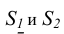 на вспомогательные плоскости проекций
на вспомогательные плоскости проекций 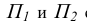 соответственно в точки
соответственно в точки 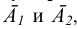 которые затем из основного центра проецирования S проецируются в точки
которые затем из основного центра проецирования S проецируются в точки 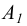 и А2 на главную картинную плоскость
и А2 на главную картинную плоскость 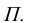
Полученный по этой схеме чертеж является обратимым, так как по известным проекциям 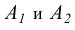 можно реконструировать положение оригинала А в пространстве.
можно реконструировать положение оригинала А в пространстве.
Большинство обратимых чертежей, применяемых в практике (аксонометрия, перспектива, эпюр Монжа), получаются по схеме рассмотренного выше метода двух изображений.
Комплексный чертеж (Эпюр Монжа)
Эпюр Монжа, он же комплексный чертеж, получается из общей схемы при следующих условиях
Главная картинная плоскость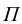 совмещается с фронтальной плоскостью проекций
совмещается с фронтальной плоскостью проекций 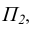 горизонтальная плоскость проекций
горизонтальная плоскость проекций 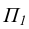 / выбирается перпендикулярной
/ выбирается перпендикулярной 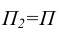 (в соответствии с рисунком 6). Центры проецирования
(в соответствии с рисунком 6). Центры проецирования 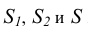 являются несобственными. При этом точка
являются несобственными. При этом точка 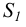 находится в направлении, перпендикулярном плоскости
находится в направлении, перпендикулярном плоскости 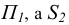 - плоскости
- плоскости 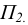
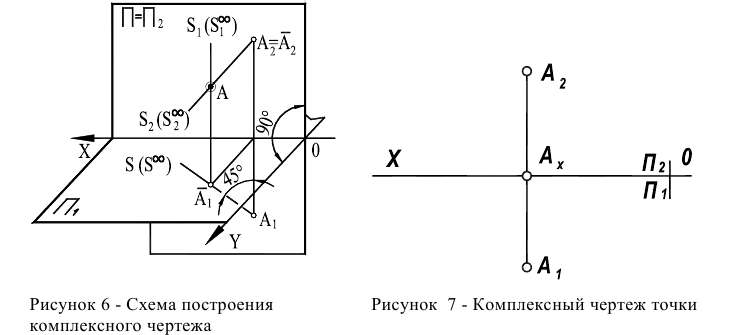
Главный центр проецирования S является несобственной точкой прямой, перпендикулярной оси 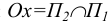 и составляющей с главной картинной плоскостью
и составляющей с главной картинной плоскостью 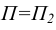 угол в 45°. Ось чертежа здесь совпадает с линией Ох.
угол в 45°. Ось чертежа здесь совпадает с линией Ох.
Изображение, получаемое на главной картинной плоскости 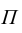 (рисунок 7), и получило название комплексного чертежа или эпюра Мопжа.
(рисунок 7), и получило название комплексного чертежа или эпюра Мопжа.
Точка A на этом чертеже задается парой проекций 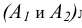 лежащих на линии связи перпендикулярной оси чертежа Ох.
лежащих на линии связи перпендикулярной оси чертежа Ох.
Традиционно плоскость 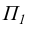 принято называть горизонтальной плоскостью проекции, а плоскость
принято называть горизонтальной плоскостью проекции, а плоскость 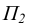 -фронтальной плоскостью проекции.
-фронтальной плоскостью проекции.
Сами же проекции называют по именам плоскостей проекции: 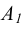 - горизонтальной проекцией точки
- горизонтальной проекцией точки 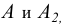 соответственно, фронтальной проекцией этой же точки.
соответственно, фронтальной проекцией этой же точки.
Еще Г. Монж мечтал о том, чтобы была возможность дополнять чертежи различных геометрических объектов их точным математическим описанием. Это требует установления связи между конструктивным способом отображения и аналитическим.
При аналитическом способе отображения пространства (моделирования) точкам ставятся в соответствие их координаты, поверхностям и линиям — уравнения и системы уравнений.
Установление связи между чертежом и аналитическим описанием объектов, на нем изображенных, возможно на основе Декартовой системы координат.
Ось чертежа можно принять за ось Ох декартовой системы координат. Координатную плоскость xOz - за фронтальную плоскость проекции 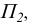 а плоскость
а плоскость
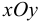 за горизонтальную плоскость проекции
за горизонтальную плоскость проекции 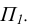
Тогда появляется возможность любую точку пространства, задаваемую на чертеже парой проекций, определять с помощью тройки чисел 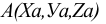 — Декартовых координат этой точки. Сам же процесс проецирования будет сводиться к построению по координатам точек
— Декартовых координат этой точки. Сам же процесс проецирования будет сводиться к построению по координатам точек 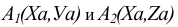 (в соответствии с рисунком 8).
(в соответствии с рисунком 8).
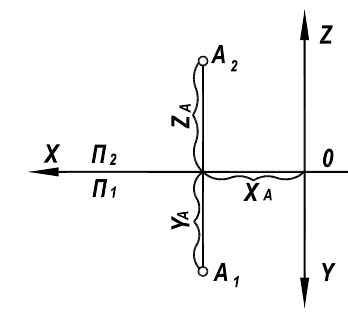
Рисунок 8.
Комплексный чертеж, ось которого совпадает с осью Ох Декартовой системы координат и на котором нанесены координатные оси Оу, Oz и зафиксировано начало Декартовых координат, получил название арифметизированного эпюра Монжа.
Такой чертеж позволяет при необходимости по аналитическому описанию объекта получать его изображение и решать обратную задачу — по чертежу получать аналитическое описание.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |