Комплексный чертеж в начертательной геометрии с примерами

Рассмотрим систему трех взаимно перпендикулярных плоскостей проекций (рис. 3.1): П₁ - горизонтальная плоскость проекций, П₂ - фронтальная плоскость проекций и П3 - профильная плоскость проекций.

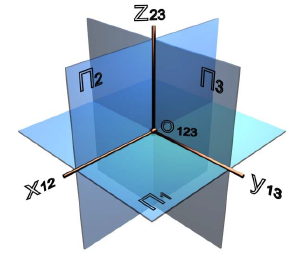
Рис. 3.1. Плоскости проекций:
x ₁₂ = Π₁

Точка пересечения трех плоскостей О123 - начало координат. Поскольку плоскости проекций бесконечны, три плоскости разделят все пространство на восемь частей - октантов. Порядок отсчета октантов (см. рис. 3.1): слева от плоскости П3 (против часовой стрелки) с первого по четвертый, справа - с пятого по восьмой.

 Направление осей x, y, zв первом октанте считается положительным. Знаки осей, продолженных за начало координат, считают отрицательными.

Для получения проекций точки А на три плоскости проекций (рис. 3.2)П₁, П₂ и П₃ через точку А проводятся проецирующие лучи [AA₁) - до пересечения с плоскостьюП₁, [AA₂) - до пересечения с плоскостью П₂ и [AA₃) - до пересечения с плоскостьюП₃. Точка A₁ - горизонтальная проекция точкиА, A₂-фронтальная проекция точкиА A3 -профильная проекция точкиА. Точки A₁₂ , A₁₃ , A₂₃ - вспомогательные, лежащие соответственно на осяхх, y, z.

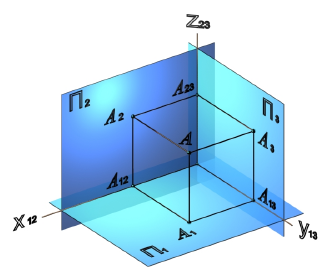
Рис. 3.2. Проецирование точки на три плоскости проекций

Для получения плоского чертежа точки А необходимо повернуть плоскость П1 вокруг оси x по часовой стрелке, а плоскость П3 - вокруг оси z до совмещения с П2. Плоскость П2, точки A2 и A12 остаются неподвижными (рис. 3.3), точки A 1 и A 13 и ось y₁ поворачиваются вместе с П1. После поворота, точкиА 1, A 12 и A2 образуют вертикальную линию связи. Точки A23 и A3, поворачиваясь вместе с П₃ и осью y₃, образуют, после поворота, горизонтальную линию связи A₂A₃. Точки A₁ и A₃ соединяются ломаной линией связи A₁A₀A₃. Вершина ломаной линии связи или точка преломления A₀ лежит на биссектрисе угла y₁O₁₂₃y₃. Множество вершин ломаных линий связи определяют условную линию, называемую постоянной прямой комплексного чертежа k123.

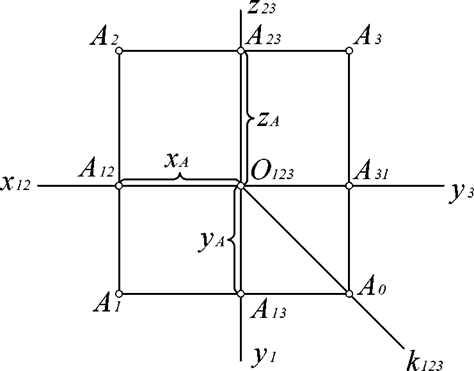
Рис. 3.3. Трехкартинный комплексный чертеж точки:
A1A13 = O123A12 = A2A23 = x - широтаА;
A1A12 = O123A13 = A23A3 = y - глубинаточкиА;
A1A12 = O123A23 = A31A3 = z - высотаточкиА

Чертеж трех совмещенных плоскостей проекций называется трехкартинным комплексным чертежом. Метод образования комплексного чертежа называют методом Монжа, в честь французского ученого Гаспара Монжа, жившего в XIX веке, первым предложившего использовать совмещенные чертежи.

• Заказать чертежи

Для решения задач в начертательной геометрии часто используются чертежи на двух совмещенных плоскостях проекций, которые называются двухкартинными комплексными чертежами (рис. 3.4).

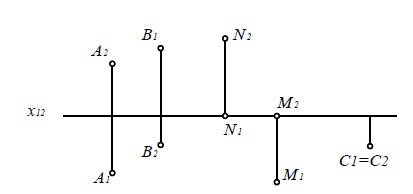
Рис. 3.4. Двухкартинный комплексный чертеж точек, занимающих различное положение относительно плоскостей проекций

1. Горизонтальная и фронтальная проекция точки A лежат на вертикальной линии связи A1A 2±х 12.
2. Фронтальная и профильная проекции точки A лежат на горизонтальной линии связи A ₂A 3±z23.
3. Горизонтальная и профильная проекция точки A лежат на ломаной линии связи A1A3 = A1A0 + A0A3, вершина которой находится на постоянной прямой комплексного чертежа& 123.

Основные свойства комплексного чертежа

Оси проекций фиксируют положение плоскостей проекций. Практически гораздо важнее установить взаимное расположение изображаемых объектов и их элементов, нежели расстояния до плоскостей проекций. На рис. 3.5,а представлен

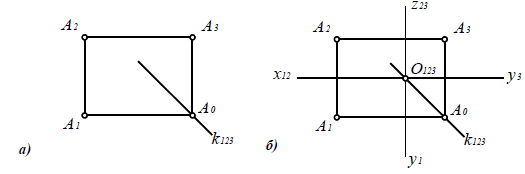
Рис. 3.5. Двухкартинные комплексные чертежи точки A:

а - безосный; б - с восстановленными осями

На технических чертежах оси не проводят, предполагая, что проецирование ведется ортогонально на три взаимно перпендикулярные плоскости проекций.

Если же оси показать необходимо, их можно восстановить (рис. 3.5,б) таким образом, чтобых 12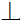A 1A2, , z₂₃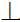A2A3, а начало координат находилось на постоянной прямой комплексного чертежа k123.