Комплексные функции электрических цепей

Содержание:

Комплексные функции электрических цепей:

Задача анализа электрической цепи состоит в определении реакции цепи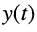

Ясно, что амплитуды и начальные фазы гармонических колебаний в цепи зависят не только от амплитуды и начальной фазы воздействия, но и от частоты его колебаний. Последнее объясняется частотной зависимостью комплексных сопротивлений элементов цепей: индуктивностей и ёмкостей. Например, реактивное сопротивление элемента индуктивности равно нулю на частоте 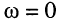(режим постоянного тока) и линейно возрастает с ростом частоты; реактивное сопротивление элемента ёмкости, наоборот, бесконечно велико на частоте 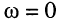и падает с ростом частоты, устремляясь к нулю при безграничном увеличении частоты, т. е. при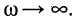

Таким образом, изменение частоты гармонического воздействия влечёт за собой изменение амплитуд и фаз гармонических колебаний во всех ветвях цепи, т. е. реакция цепи является не только функцией времени, но и функцией частоты.

Анализ электрической цепи в частотной области состоит в выявлении закономерностей изменения реакции в зависимости от частоты.
 

Определение комплексных функций электрических цепей

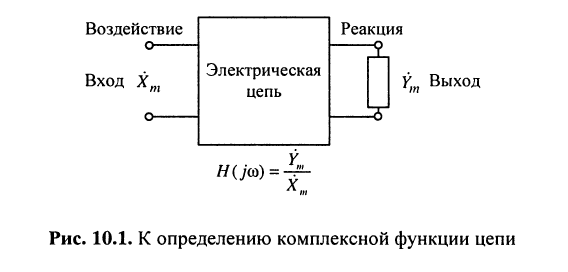
Пусть на вход цепи, представляющей собой четырёхполюсник (рис. 10.1), воздействует гармоническое колебание 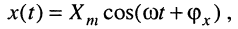комплексная амплитуда которого

Реакция будет полностью определяться частотными свойствами самого четырёхполюсника. Поскольку цепь линейная, то частота гармонического колебания не изменится, а вот амплитуда реакции 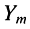и начальная фаза реакции 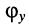будут отличаться от амплитуды 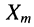и начальной фазы воздействия  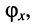что ясно хотя бы из рассмотрения частотных свойств элементов индуктивности и ёмкости.

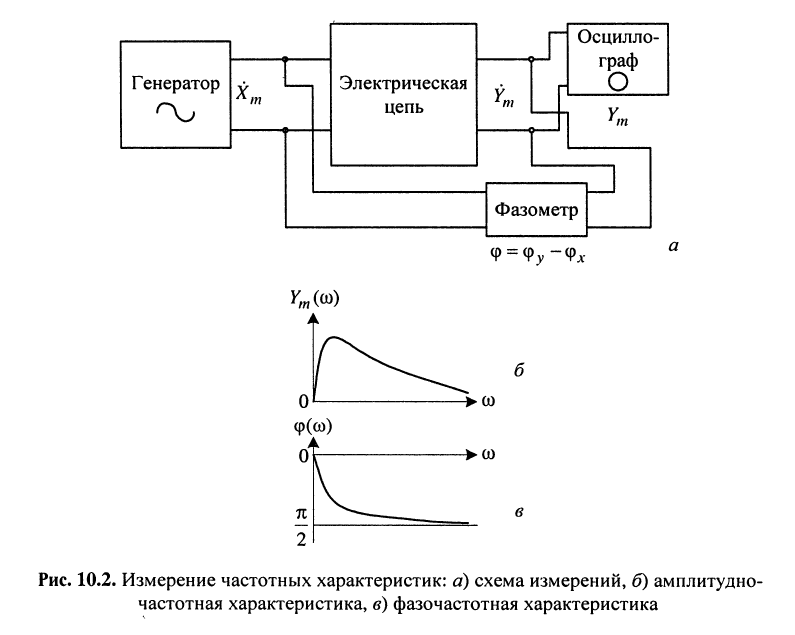
Особый интерес представляет соотношение вход/выход, которое отображает частотные свойства цепи, показывающие, каким образом откликается цепь на конкретное гармоническое колебание. Изучение частотных свойств цепи можно провести, например, с помощью схемы, показанной на рис. 10.2, а: на входе цепи действует генератор гармонических колебаний, к её выходу подключён осциллограф, а параллельно цепи подключён фазометр.

Будем последовательно подавать на вход электрической цепи различные гармонические колебания известной частоты 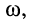амплитуды 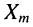и с произвольной начальной фазой  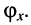Обычно при измерениях амплитуду гармонических колебаний устанавливают постоянной 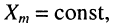которую можно без потери общности результатов принять за 1. Все дальнейшие измерения будем производить при условии установления колебаний, т. е. в режиме установившихся колебаний.

Измеряя с помощью осциллографа амплитуду колебания 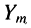на выходе цепи, построим график зависимости амплитуды от частоты 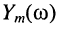(рис. 10.2, б). Эту характеристику называют амплитудно-частотной характеристикой цепи.

С помощью фазометра измерим разность между начальной фазой гармонического колебания на входе 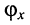и фазой соответствующего гармонического колебания на выходе 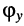, и построим график (рис. 10.2, в) частотной зависимости 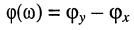разности начальных фаз реакции и воздействия. Такую характеристику называют фазочастотной характеристикой цепи.

Однако такая процедура выявления частотных свойств цепи, во-первых, трудоёмка и, во-вторых, не позволяет получить общий характер частотных зависимостей произвольной цепи. В то время как знание закономерностей изменения реакции цепи от частоты позволяет точно определить возможность передачи по этой цепи сигнала, распределённого по частоте, т. е. занимающего некоторую область частот от до

Очевидно, что отношение вход/выход, т. е. отношение реакции к воздействию, наиболее просто выразить через отношение комплексных амплитуд гармонического воздействия и гармонической реакции, поскольку комплексные амплитуды содержат амплитуду и начальную фазу гармонического колебания.

Определение:

Комплексной частотной характеристикой цепи 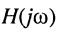(КЧХ) называется отношение комплексной амплитуды реакции 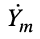к комплексной амплитуде воздействия  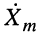в установившемся режиме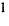(рис. 10.1):

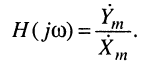       (10.1)

Размерность комплексной частотной характеристики зависит от того, какие величины (напряжения или токи) выбраны в качестве реакции и воздействия (рис. 10.3).

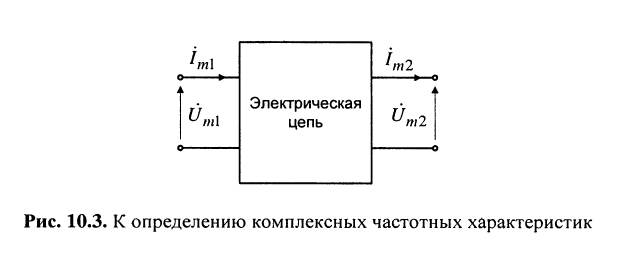
В связи с этим различают следующие виды КЧХ (табл. 10.1), смысл которых ясен из смысла входящих в них реакций и воздействий: безразмерные 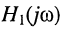и 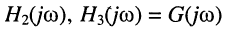имеет размерность проводимости, а 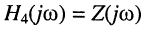— размерность сопротивления.

По определению (10.1) комплексная амплитуда реакции равна произведению комплексной передаточной функции воздействия на комплексную частотную характеристику цепи:

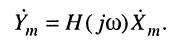      (10.2)

Как и всякая комплексная функция, КЧХ может быть записана как в показательной

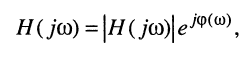       (10.3)

так и в алгебраической форме

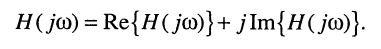         (10.4)

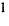 Это отношение также называют комплексной передаточной функцией или комплексным коэффициентом передачи.

Найдём выражения для модуля 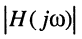и аргумента 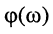комплексной функции (10.3) и (10.4), которые являются функциями частоты, поэтому амплитуды и начальные фазы также являются функциями частоты: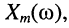 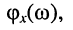,  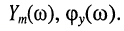 При этих условиях имеем:

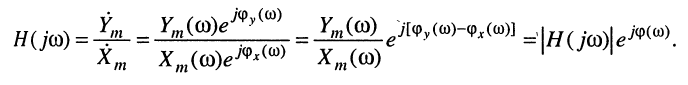        (10.5)

Полученное соотношение позволяет определить важнейшие частотные характеристики линейных цепей: амплитудно-частотную (модуль (10.5)) и фазочастотную (аргумент (10.5)). Дадим определения этим характеристикам.

Определение:

Амплитудно-частотной характеристикой (АЧХ) 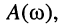, называется частотная зависимость отношения амплитуды гармонической реакции к амплитуде гармонического воздействия в установившемся режиме:

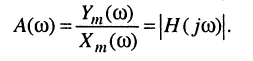       (10.6)

Определение:

Фазочастотной характеристикой (ФЧХ) 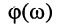называется частотная зависимость разности начальных фаз гармонической реакции и гармонического воздействия в установившемся режиме:

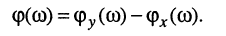
Эти же характеристики нетрудно определить из алгебраической формы представления КЧХ (10.4):

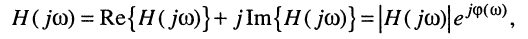
откуда АЧХ

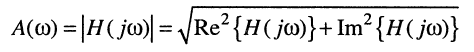       (10.8)

и ФЧХ

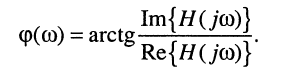     (10.9)

Среди комплексных частотных характеристик выделяют комплексные входные функции-.

□ функцию входного сопротивления

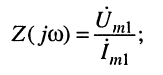      (10.10)

□ функцию входной проводимости

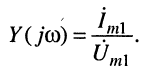      (10.11)

Из определений частотных характеристик следуют важные выводы:

• комплексная частотная характеристика содержит в себе амплитудно-частотную и фазочастотную характеристики цепи;
• комплексная частотная характеристика цепи численно равна комплексной амплитуде реакции цепи на воздействие,                                 описываемое единичной гармонической функцией
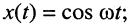
• частотные характеристики электрической цепи зависят только от параметров самой цепи и не зависят от воздействия.

Расчёт частотных характеристик

Расчёт частотных характеристик при известном воздействии 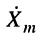осуществляется в следующем порядке:

1. Рассчитывается комплексная амплитуда реакции
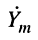
2. Определяется комплексная частотная характеристика (КЧХ) заданной цепи согласно (10.1).
3. Записывается выражение для АЧХ как модуль КЧХ согласно (10.6) или (10.8)    и строится график АЧХ.
4. Записывается выражение для ФЧХ как аргумент КЧХ согласно (10.7) или (10.9)    и строится график ФЧХ.

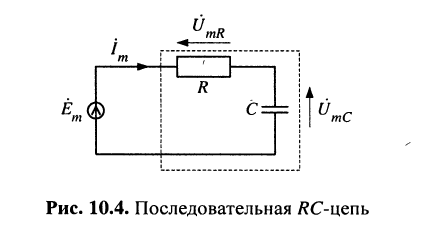
В качестве примера рассчитаем частотные характеристики последовательной RС-цепи (рис. 10.4).

Задача 10.1.

Воздействием на последовательную RС-цепь является напряжение 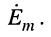 Найти выражения и построить графики для КЧХ, АЧХ и ФЧХ цепи для двух случаев:

реакцией является ток в цепи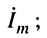

реакцией является напряжение на ёмкости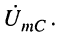

Решение.

Реакцией является ток в цепи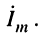

Рассчитаем комплексную амплитуду тока:

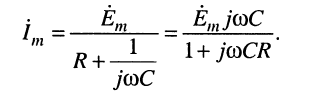
Определим комплексную частотную характеристику как отношение комплексной амплитуды тока к комплексной амплитуде напряжения воздействия:

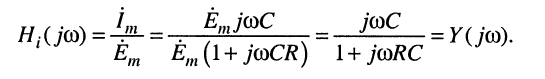      (10.12)

Полученное соотношение говорит о том, что в данном случае КЧХ имеет размерность проводимости.

Исходя из (10.12), запишем выражение амплитудно-частотной характеристики:

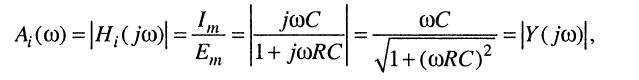       (10.13)

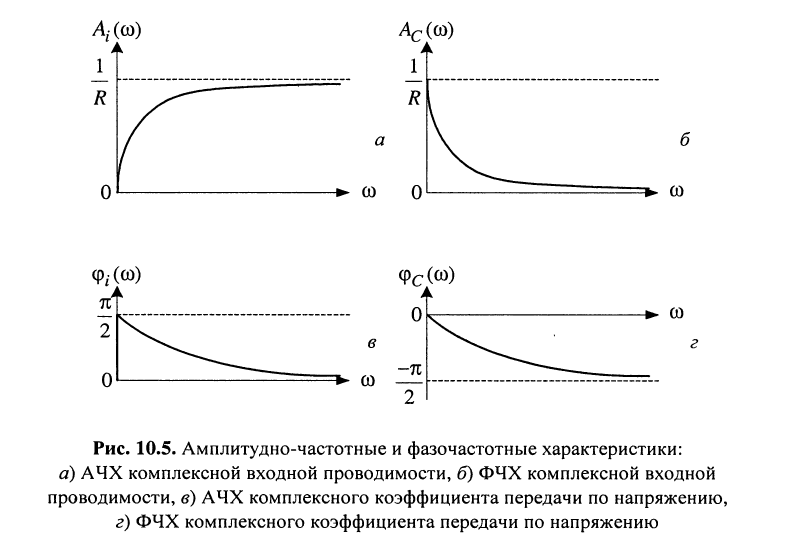
которая представляет собой полную частотно зависимую входную проводимость цепи (рис. 10.5, а).

Запишем выражение для ФЧХ как аргумент КЧХ, который согласно (10.5) и (10.7) можно представить в виде разности аргументов числителя и знаменателя КЧХ (10.12):

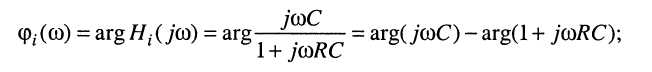
но аргумент числителя равен:

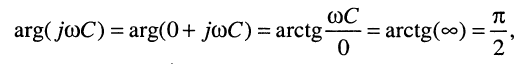
аргумент знаменателя равен:

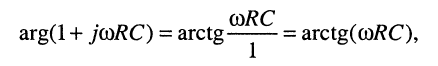
поэтому ФЧХ цепи (рис. 10.5, б), когда в качестве реакции принят ток, имеет вид:

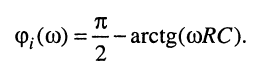   (10.14)

□ Реакцией является напряжение на конденсаторе 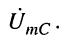Тогда вновь по определению КЧХ имеем:

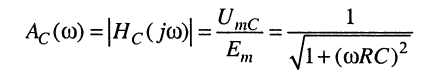
эта КЧХ является безразмерной величиной и часто называется комплексным коэффициентом передачи по напряжению.

Из формулы КЧХ (10.15) нетрудно получить выражения для АЧХ (рис. 10.5, в)

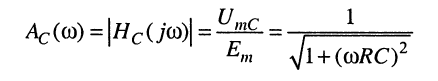
и ФХЧ  (рис.10.5, г)

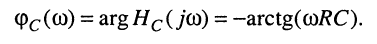
Таким образом, задача решена.

Комплексная частотная характеристика, как было отмечено ранее, содержит в себе АЧХ и ФЧХ цепи и поэтому может быть представлена графически в виде годографа (рис. 10.6), если её записать в алгебраической форме (10.4) и учесть соотношения (10.8) и (10.9).

На годографе каждому значению частоты со соответствует свой вектор, модуль которого равен АЧХ, а фаза — ФЧХ цепи. Годограф строят для частот со в диапазоне от 0 до   На рис. 10.6 представлен годограф комплексной частотной характеристики (10.15).

Годограф построен по точкам следующим образом:

на частоте 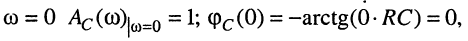 т. е. точка лежит на вещественной оси, её координата (1, 0);

на частоте т. е. точка лежит в начале координат (0, 0);

величина 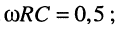при этом

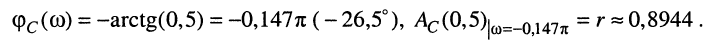
Аналогичным образом вычисляются интересуемые точки; направление перемещения конца вектора указывают стрелкой в сторону увеличения частоты. Иногда годограф КЧХ называют амплитудно-фазовой характеристикой цепи.
 

Логарифмические частотные характеристики

Обычно значения амплитудно-частотных характеристик изменяются в очень широких пределах. В связи с этим более удобным оказывается логарифмический масштаб их представления. Такие характеристики называются логарифмическими. Они находятся в результате логарифмирования безразмерной амплитудно-частотной характеристики. Это означает, что согласно табл. 10.1 логарифмическими могут быть только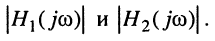

Для оценки АЧХ введено понятие логарифмической амплитудно-частотной характеристики (ЛAX)

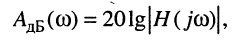      (10.16)

которая имеет размерность "децибел" (дБ). В активных цепях, где имеет место превышение амплитуды реакции над амплитудой воздействия, ЛAX 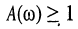называют также логарифмическим усилением.

В пассивных цепях, где усиление в принципе невозможно, всегда 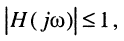поэтому имеет место ослабление

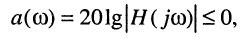         (10.17)

причём 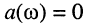только при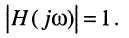

Часто в системах многоканальной связи используют понятие затухания Ь(со), отличающееся от ослабления только знаком:

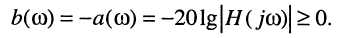      (10.18)

Тогда отрицательное затухание имеет смысл усиления.

В большинстве практических задач, включая синтез фильтров и сравнительное исследование свойств АЧХ цепей различной природы, более удобным оказывается введение нормированной АЧХ 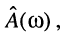 которая представляет собой отношение текущего значения АЧХ 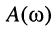к её максимальному значению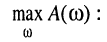 

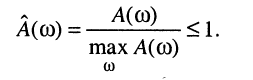     (10 19)

Нормированная АЧХ является безразмерной величиной и может использоваться для характеристики как пассивных, так и активных цепей. Соответствующие ей характеристики затухания и ослабления имеют вид:

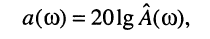      (10.20)

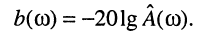       (10.21)

Из смысла нормированной АЧХ ясно, что нормированная АЧХ пассивных цепей не может превосходить единицу:

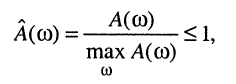
а ослабление (затухание) не может быть больше 0 дБ (меньше 0 дБ).

Нормированная АЧХ активных цепей может превосходить единицу, а ослабление (затухание) может быть больше 0 дБ (меньше 0 дБ). Далее рассматриваются пассивные цепи, если не оговорено другое.

Примеры нормированной АЧХ и соответствующей ей характеристики ослабления пассивной цепи приведены на рис. 10.7 соответственно.

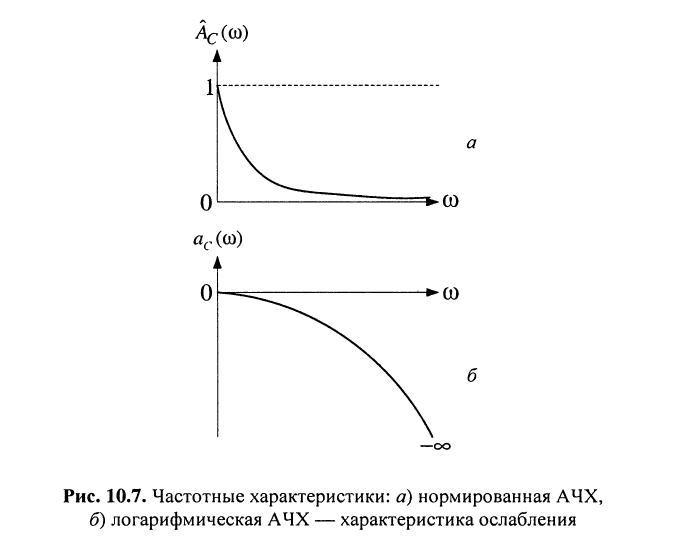
Здесь

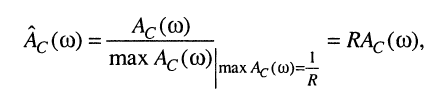
причем

В соответствии с нормированной АЧХ характеристика ослабления располагается в четвёртом квадранте так, что

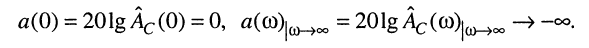
Поясним смысл децибела. Пусть на некоторой частоте со* ослабление составляет 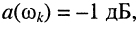что отражается равенством:

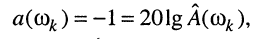
откуда значение нормированной АЧХ на этой частоте равно:

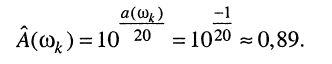     (10-22)

Последнее означает, что на частоте 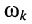значение ненормированной АЧХ составляет 0,89 от максимума АЧХ:

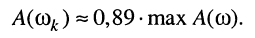
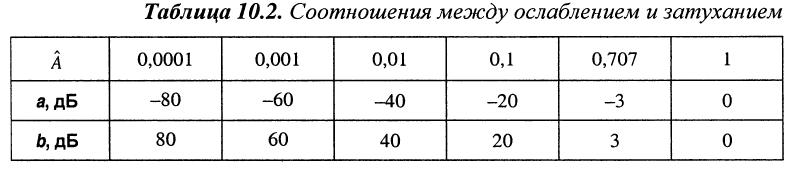
Соответствие между нормированными значениями 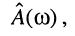выраженными в разах, ослаблением и затуханием 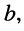выраженными в децибелах, приведено в табл. 10.2

.

Ещё раз следует обратить внимание на то, что при 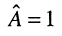ослабление (затухание) 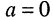.  При уменьшении АЧХ относительно 1 ослабление принимает отрицательные значения, а затухание — положительные.