Колебания в линиях без потерь

Содержание:

Колебания в линиях без потерь:

Любая реальная линия всегда обладает потерями. Однако на практике во многих случаях применяются очень короткие линии, собственное затухание которых составляет тысячные доли децибел, а длина их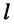

В подобных линиях величины первичных параметров R и G очень малы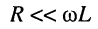

Определение:

Линии, в которых удовлетворяются условия 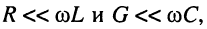 называются линиями с пренебрежимо малыми потерями или линиями без потерь.

Такая идеализация справедлива для линий, работающих в области сверхвысоких частот (фидеров, измерительных линий, согласующих СВЧ устройств и т. д.). Она позволяет более ясно представить волновые процессы в длинных линиях и существенно упростить расчёты.

25.1.1. Вторичные параметры и уравнения передачи длинной линии без потерь

При условии равенства нулю первичных параметров R = 0 и G = 0 вторичные параметры линии без потерь принимают вид:

коэффициент распространения линии без потерь чисто мнимый:

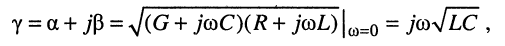
    коэффициент затухания равен нулю

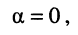
    коэффициент фазы линейно зависит от частоты

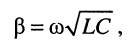
    волновое сопротивление является чисто активным (резистивным)

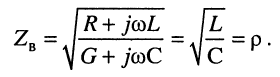
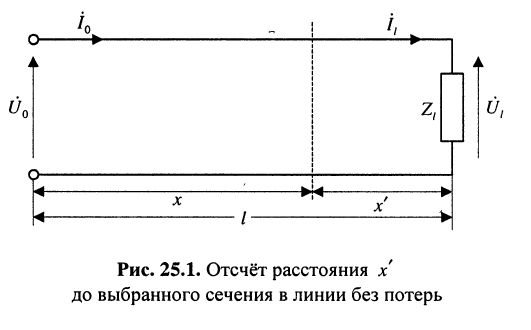
Уравнения передачи линии без потерь, описывающие распределение напряжений и токов в режиме гармонических колебаний, можно получить из выражений (24.16) и (24.17) после подстановки в них соответствующих вторичных параметров. Необходимо также учесть, что в теории длинных линий без потерь общепринято отсчитывать расстояние до выбранного сечения не от начала линии, а от её конца, как показано на рис. 25.1. 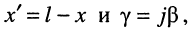Тогда, произведя в уравнениях (24.16) и (24.17) замены получаем:

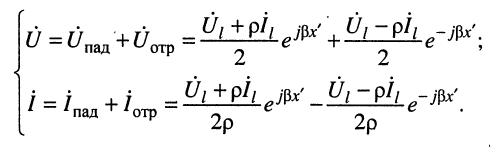      (25.1)

Группируя слагаемые в уравнениях (25.1) и пользуясь формулой Эйлера

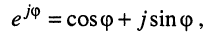приведём систему уравнений к более удобному виду:

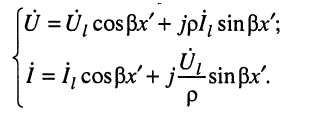         (25 2)

Выразим напряжение 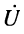и ток 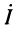через напряжение 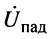и ток 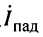падающей волны. Рассмотрим первое уравнение в (25.1):

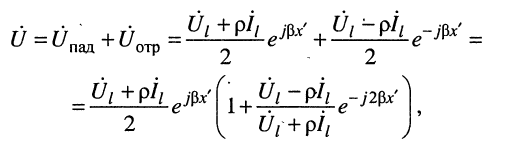
в котором стоящая в скобках дробь представляет собой коэффициент отражения р линии без потерь. Действительно,

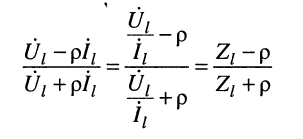
и согласно определению (24.15) имеем:

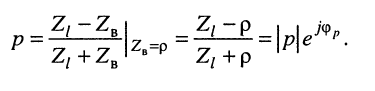       (23.5)

Полученный результат позволяет записать выражение для комплексной амплитуды напряжения

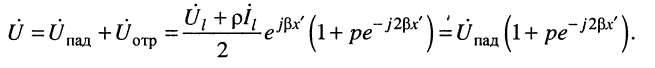       (25.4)

Аналогичные преобразования второго уравнения в (25.1) приводят к записи комплексной амплитуды тока в виде:

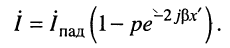         (25.5)

Уравнения (25.4) и (25.5) являются уравнениями передачи длинной линии без потерь, которые удобно представить в виде системы уравнений:

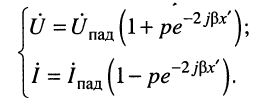        (25.6)

Важно:

в длинных линиях без потерь модуль коэффициента отражения при нагрузке линии на любой пассивный двухполюсник не может превышать единицы.

Действительно, поскольку вещественная часть комплексного пассивного сопротивления нагрузки 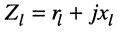всегда не меньше нуля 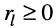, то имеет место неравенство

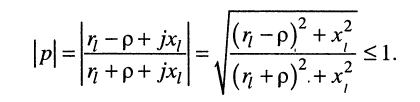         (25.7)

По этой причине амплитуда отражённой волны в линии без потерь при любой пассивной нагрузке не может превышать амплитуду падающей волны.

Режим бегущей волны (согласованной нагрузки) в линии без потерь

Рассмотрим частный случай, когда сопротивление нагрузки линии без потерь является чисто активным и равным волновому сопротивлению

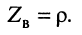
Понятно, что при этом условии отношение напряжения на нагрузке равно произведению волнового сопротивления на ток в нагрузке 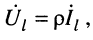а уравнения передачи принимают вид:

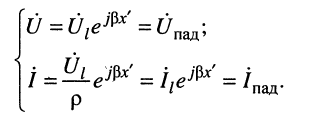        (25.8)

Переходя от комплексных амплитуд к мгновенным значениям колебаний, из (25.8) получаем:

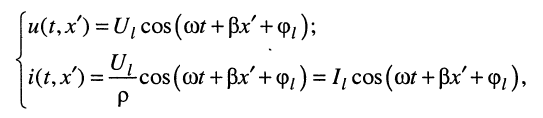          (25.9)

где — начальная фаза колебаний в конце линии.

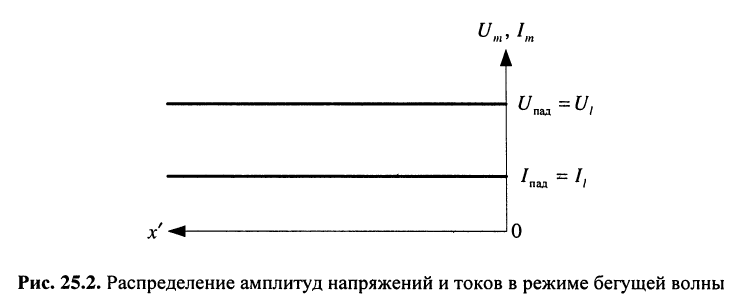
Из (25.9) можно сделать следующие выводы (рис. 25.2):

• начальные фазы напряжения 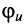и тока 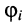в конце линии равны друг другу 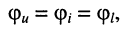поскольку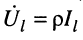
• отражённая волна отсутствует;
• колебания напряжения и тока в любом сечении линии происходят в фазе;
• амплитуды тока и напряжения остаются неизменными по всей линии.

Режим стоячих волн

Рассмотрим режим длинной линии, когда модуль коэффициента отражения равен единице: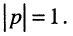 Это приводит к полному отражению падающей волны,

что согласно формуле коэффициента отражения для линии без потерь (25.7) возможно в трёх случаях:

• линия замкнута накоротко ;
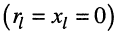• линия разомкнута
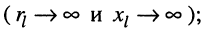
• линия нагружена на чисто реактивное сопротивление .

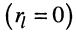Изучим указанные варианты, для чего положим для простоты значение начальной фазы падающей волны в конце линии равным нулю 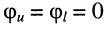и получим мгновенные значения напряжения и тока.

Обратимся к системе уравнений (25.6) и вновь рассмотрим уравнение для напряжения, где

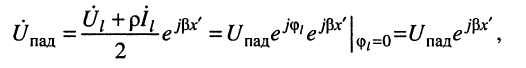
поэтому
 

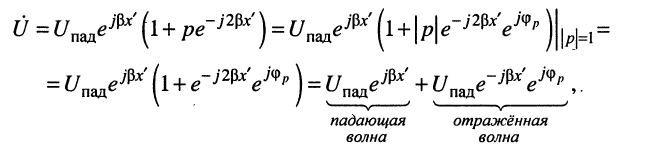
где 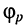— аргумент коэффициента отражения. Отсюда получаем мгновенные значения напряжения:

падающей волны

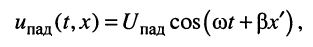
отражённой волны

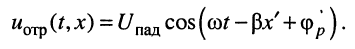
Следовательно, мгновенное значение напряжения в линии без потерь имеет вид:

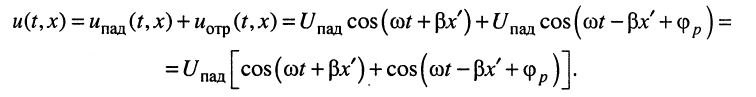
Применение к последнему равенству известной формулы для суммы косинусов

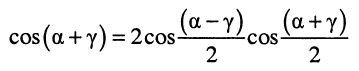
дает следующий результат:

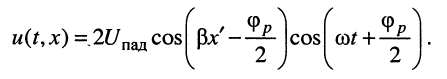       (25.11)

Аналогично, с использованием формулы для разности косинусов, можно получить выражение для тока:

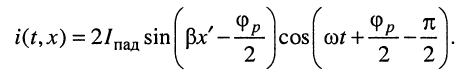
Изучим выражение (25.11). Оно отображает гармоническое колебание с частотой 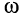и амплитудой

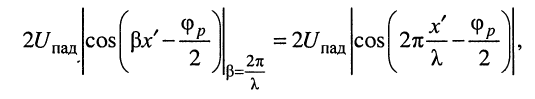
значения которой изменяются вдоль линии следующим образом:

в сечениях линии, где

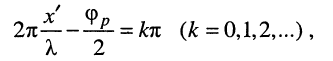
амплитуда гармонического напряжения принимает максимальное значение, вдвое превышающее амплитуду напряжения падающей волны;

в сечениях линии, где

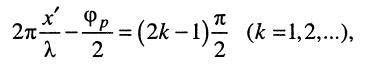
амплитуда напряжения равна нулю .

Картина распределения напряжения вдоль линии для двух моментов времени  показана на рис. 25.3.

Рассмотренный режим колебаний в линии называется режимом стоячих волн.

Режим стоячих волн характеризуется (рис. 25.3):

    наличием в линии сечений, в которых амплитуда колебаний равна нулю, и сечений, в которых она максимальна; первые называются узлами, вторые — пучностями стоячей волны;

    удалённостью смежных узлов и смежных пучностей друг от друга на расстояние, равное половине длины падающей (отражённой) волны, что следует из (25.13) и (25.14);

    расстоянием между узлом и смежной пучностью, равным четверти длины волны;

В режиме короткого замыкания линии 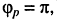, поэтому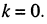

    синфазностью колебаний напряжения в любых сечениях (точках), находящихся между смежными узлами;

    скачкообразным изменением фазы колебаний на при переходе через узел.

Анализируя выражение (25.12) для тока, получаем те же выводы, что и для напряжения, но узлы тока совпадают с пучностями напряжения, а пучности тока — с узлами напряжения, что показано (рис. 25.4) на примере распределения амплитуд напряжений и токов в короткозамкнутой линии (режим короткого замыкания): в конце линии расположен узел напряжения 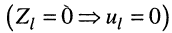, которому соответствует пучность тока.

Распределение амплитуд и фаз можно найти из (25.11) и (25.12), если положить 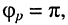поскольку при коротком замыкании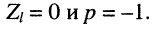

Распределение амплитуд напряжений и токов в разомкнутой линии (режим холостого хода) показано на рис. 25.5: в конце линии располагаются узел тока и пучность напряжения.

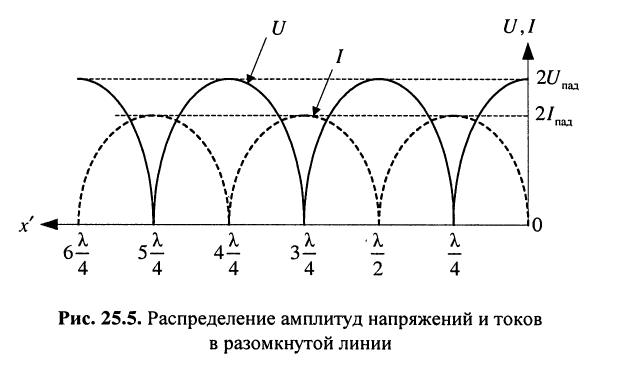
При нагрузке линии реактивным сопротивлением первый узел или первая пучность напряжения располагается на удалении четверти длины волны от конца линии.

Выводы:

• в режиме стоячих волн не происходит рассеяния энергии, подведённой ко входу линии, поскольку в самой линии, по определению, отсутствуют потери R = G = 0, а сопротивление нагрузки, как указано в начале данного раздела, или равно нулю, или бесконечно велико, или чисто реактивно;
• по этой причине разность фаз колебаний напряжения и тока в любом сечении линии равна 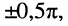что видно из сравнения выражения для напряжения (25.10) и для тока (25.11);
• последнее означает, что входное сопротивление линии является чисто реактивным.

Режим смешанных волн

Изученные режимы бегущих и стоячих волн соответствуют предельным случаям, в первом из которых отражённая волна отсутствует 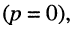а в других — амплитуды падающей и отражённой волн одинаковы 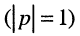во всех сечениях длинной линии.

Рассмотрим режим линии без потерь при несогласованной нагрузке, когда 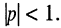Ясно, что в таком случае отражённая волна присутствует, причём её амплитуда меньше амплитуды падающей волны.

На основании (25.10) запишем решение для мгновенного значения напряжения при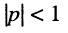

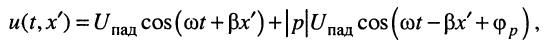
где 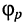 — аргумент коэффициента отражения.

Покажем, что это выражение описывает сумму бегущей и стоячей волн. Для этого в правой части уравнения вычтем и прибавим слагаемое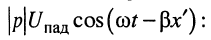

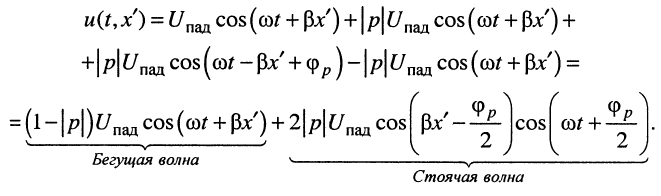          (25.15)

Таким образом, в рассматриваемом режиме происходит наложение бегущей (первое слагаемое) и стоячей (второе слагаемое) волн. По этой причине подобный режим колебаний называется режимом смешанных волн. Графики распределения амплитуд напряжения и тока в данном режиме показаны на рис. 25.б.

В узлах напряжений стоячей волны, где 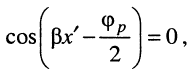 амплитуда напряжения в линии совпадает с амплитудой бегущей волны и минимальна: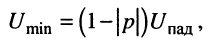 

Т. е. равна разности амплитуд падающей и отражённой волн.

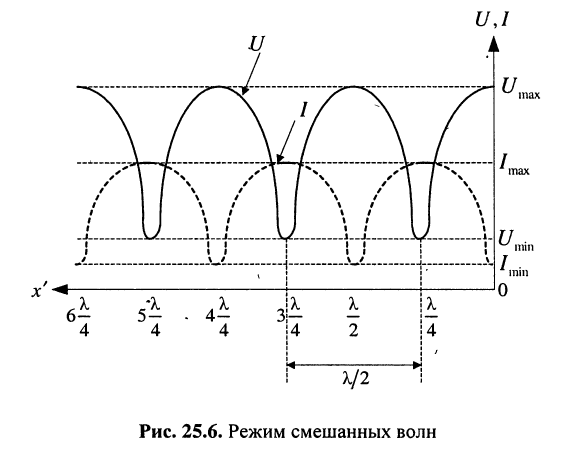
Соответствующие сечения отстоят друг от друга на расстоянии, равном половине длины волны 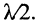Пучности стоячей волны располагаются в тех сечениях, где  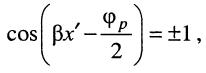т. е. там, где 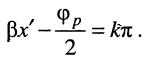Подставляя в (25.15)

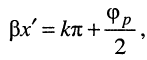   получаем:

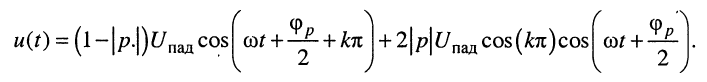
Поскольку

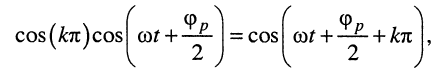
окончательно имеем:
 

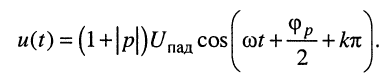
Следовательно, в сечениях, соответствующих пучностям стоячей волны, амплитуды падающей и отражённой волн складываются, и напряжение в этих сечениях максимально:

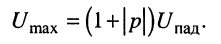
В силу того, что в стоячей волне узлам напряжения соответствуют пучности тока и наоборот, то в режиме смешанных волн в сечениях, где амплитуда напряжения минимальна (максимальна), амплитуда тока максимальна (минимальна) и составляет:

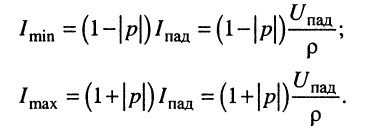
Определение:

Отношение минимальной и максимальной амплитуд колебаний напряжения (тока) в линии называется коэффициентом бегущей волны.

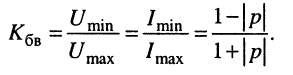     (25.16)

Режиму бегущей волны соответствует 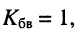а режиму стоячей волны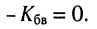

Входное сопротивление линии без потерь

Определение:

Входным сопротивлением линии 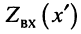в сечении, удалённом на расстояние 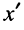от конца линии, называют отношение комплексных амплитуд напряжения и тока в этом сечении.

Согласно (24.33) имеем:

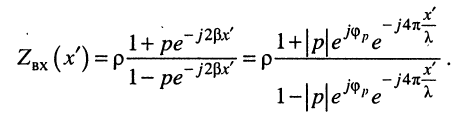             (25.17)

Поскольку амплитуды падающей и отражённой волн в линии без потерь остаются, как было показано ранее, неизменными по всей длине линии, и амплитуды повторяются с периодом, равным половине длины волны, то и входное сопротивление линии обладает тем же периодом:

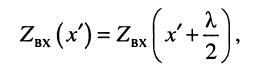
что также видно из (25.17).

Действительно, вычисляя показатель правой экспоненты в сечении линии, равном 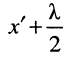, получаем:

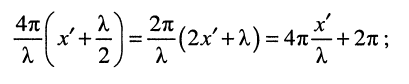
а при таком показателе значение экспоненты

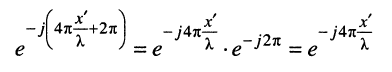
 не меняется.

Рассмотрим два важных для практики режима, используемые для определения первичных и вторичных параметров длинных линий при их строительстве и эксплуатации: режим КЗ и режим XX.

Режим короткого замыкания линии

Для этого режима коэффициент отражения 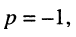а входное сопротивление, согласно (25.17),

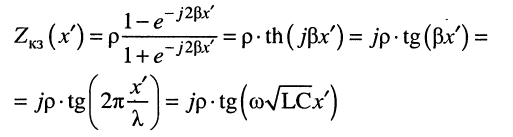           (25.18)

чисто реактивно. Это является следствием того, что электрическая энергия при коротком замыкании (КЗ) линии не рассеивается. График входного сопротивления в режиме КЗ (рис. 25.7) представляет собой обычную тангенсоиду как функцию координаты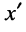. В пучностях напряжений (узлах тока) сопротивление короткозамкнутой линии бесконечно велико (имеет место полюс сопротивления), а в узлах напряжения (пучностях тока) оно равно нулю (имеет место нуль сопротивления). На участке линии, длина которого равна половине длины волны, сопротивление линии изменяется от  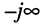до 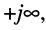 что даёт возможность подобрать такой отрезок длинной линии без потерь, который при заданной длине волны (частоте колебаний) имел бы любое наперёд определённое реактивное сопротивление как индуктивного, так и ёмкостного характера.

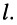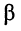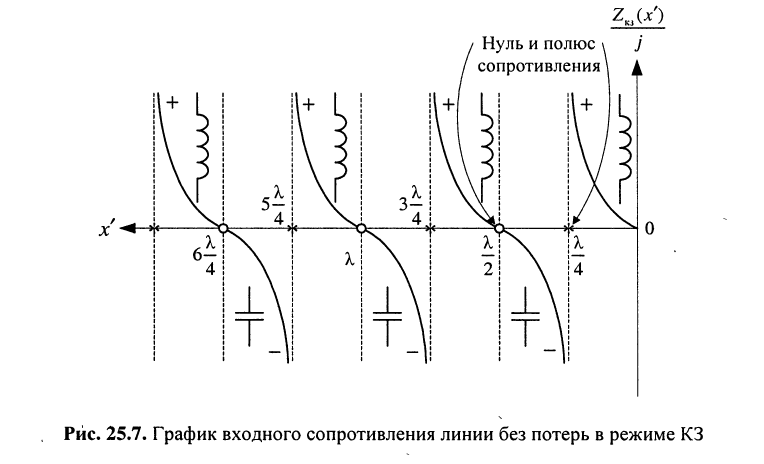
Положение полюсов и нулей сопротивления зависит от частоты колебания, действующего в линии длиной . Эта зависимость объясняется тем, что коэффициент фазы является функцией частоты (24.6). Найдём частоты 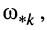 на которых располагаются полюсы сопротивления, для чего в (25.18) заменим 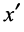на .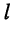

Ясно, что функция 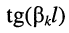обращается в бесконечность, когда её аргумент принимает значения 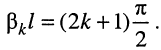При этом условии и равенстве (24.6) получаем выражение

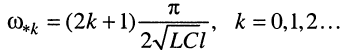       (25.19)

Отсюда первый полюс сопротивления расположен на частоте

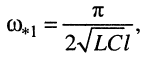         (25.20)

на которой короткозамкнутая линия ведет себя как параллельный колебательный LC-контур, имеющий резонансную частоту .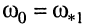

Режим холостого хода линии

В режиме холостого хода (XX) р = 1 входное сопротивление 

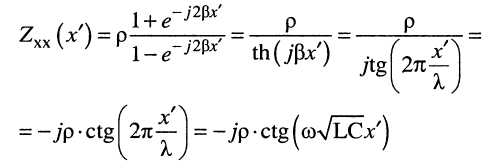
также чисто реактивно. Его график представлен на рис. 25.8.

Сравнение графиков рис. 25.7 и 25.8 показывает, что один из них сдвинут относительно другого на четверть длины волны. Это естественно, поскольку разомкнутую на конце линию можно нарастить короткозамкнутым четвертьволновым отрезком, имеющим большое входное сопротивление, что никак не нарушит режима в линии.

Согласно (25.21) полюсы сопротивления в режиме XX линии длиной 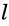будут располагаться на частотах  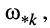где 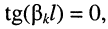 т. е. на тех частотах, на которых располагаются нули сопротивления короткозамкнутой линии, а именно:

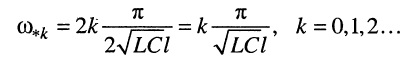       (25.22)

Выводы из разд. 25.4.1 и 25.4.2:

• при любой из частот (25.19) и (25.22) по длине линии укладывается ровно 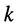четвертьволновых отрезков;
• нули и полюсы сопротивления перемежаются (чередуются);
• на частотах, на которых располагаются полюсы (нули) сопротивления короткозамкнутой линии, располагаются нули (полюсы)              разомкнутой линии;
• сопротивление линии возрастает с ростом частоты.

Входное сопротивление линии с произвольной нагрузкой

Рассмотрим выражение (25.17) при произвольном комплексном сопротивлении нагрузки 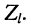. Входное сопротивление будет принимать максимальное по модулю значение в тех сечениях линии, где числитель максимален, а знаменатель минимален. Это возможно, когда

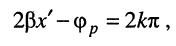
т. е. в сечениях

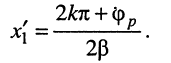
В таких случаях входное сопротивление чисто активно и максимально:

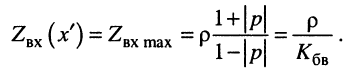
С другой стороны, входное сопротивление минимально по модулю в тех сечениях линии, где числитель минимален, а знаменатель максимален. Это возможно, когда

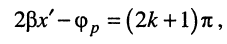
т. е. в сечениях

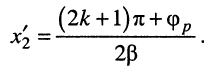
В таких случаях входное сопротивление также чисто активно, но минимально:

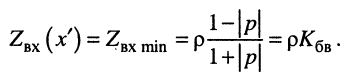
Понятно, что расстояние между смежными сечениями линии, в которых её входное сопротивление чисто активно и максимально (минимально), равно половине длины волны в линии, поскольку на таком расстоянии относительно друг друга расположены максимумы (минимумы) амплитуды напряжения. А посредине между ними расположены минимумы (максимумы) активной части входного сопротивления линии.

Действительно, расстояние 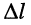между смежными сечениям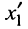и (или 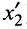) составляет

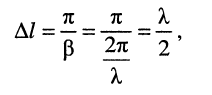
а расстояние 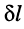между смежными сечениям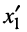и и 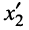равно:

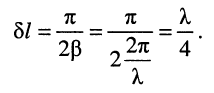
В промежутках между этими сечениями линии её входное сопротивление является комплексным. График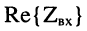и и 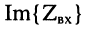показаны на рис. 25.9.

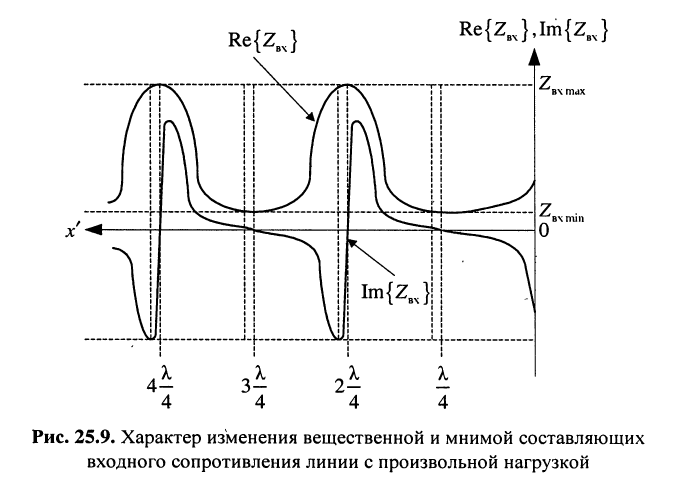
Таким образом, вещественная составляющая входного сопротивления 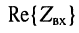находится в границах:

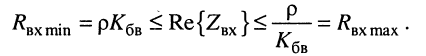
Примеры применения длинных линий с пренебрежимо малыми потерями

При синтезе разнообразных линейных электрических цепей частр существенную роль играет относительная ширина рабочей полосы частот 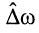, под которой понимают отношение рабочей полосы частот 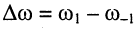к среднегеометрической частоте рабочей полосы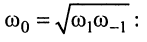

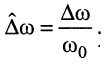
Чем меньше это отношение, тем уже относительная ширина. В большинстве практически важных случаев относительная ширина рабочей полосы частот, в которой используется линия с пренебрежимо малыми потерями, является весьма узкой. По этой причине можно без большой погрешности пользоваться характеристиками линии для среднегеометрической частоты рабочей полосы частот.

Такой "одночастотный" подход позволяет строить разнообразные устройства на отрезках длинных линий с пренебрежимо малыми потерями.

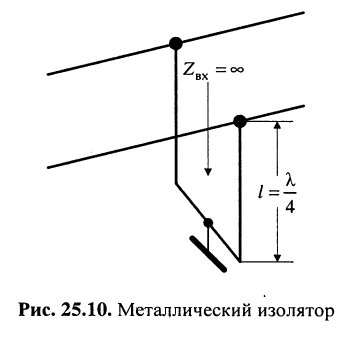
Металлический изолятор

Входное сопротивление короткозамкнутого четвертьволнового отрезка линии стремится к бесконечности (рис. 25.7):

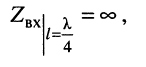
что позволяет использовать такой отрезок линии в качестве металлического изолятора на частоте 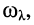, длина волны которой 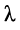в четыре раза больше длины самого отрезка.

При наличии малых потерь (собственное затухание линии 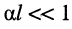) мнимая составляющая входного сопротивления четвертьволнового отрезка равна нулю

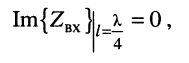
поэтому такой отрезок обладает только вещественным сопротивлением

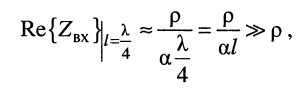
которое значительно больше волнового сопротивления линии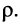

Такие изоляторы по своим электрическим и конструктивно-механическим параметрам превосходят изоляторы из диэлектриков. Их используют для подвески двухпроводных воздушных фидерных линий (рис. 25.10): жёсткие металлические трубы или прутья подсоединяются к линии, их нижние концы заземляются, чем обеспечивается режим КЗ.

Важно:

для чётных гармоник 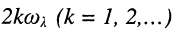рабочей частоты 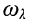металлический изолятор представляет малое сопротивление, приближённо равное 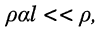, поэтому такой отрезок может использоваться в качестве фильтра, подавляющего все чётные гармоники частоты 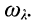Это объясняется следующим: в режиме КЗ на частотах, где у линии без потерь располагаются нули сопротивления 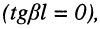входное сопротивление линии с малыми потерями оказывается равным (24.30)

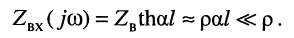
Колебательный контур

Колебательные системы техники сверхвысоких частот (СВЧ) не могут быть построены на катушках индуктивности и конденсаторах, поэтому взамен их используются отрезки линий с малыми потерями в режиме короткого замыкания или холостого хода.

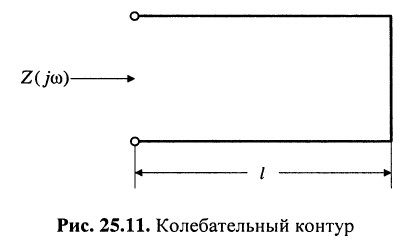
Согласно (25.20) короткозамкнутый отрезок линии (рис. 25.11) в области первого из полюсов сопротивления (рис. 25.7) эквивалентен параллельному колебательному контуру, имеющему резонансную частоту

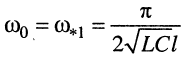
и резонансное сопротивление

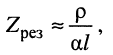
которое можно получить из общей формулы (24.33) при условии, что для короткозамкнутой линии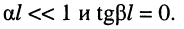

Ширину полосы пропускания такого колебательного контура на уровне 0,707 можно найти по приближённой формуле

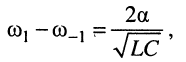
также получаемой из (24.33).

Добротность короткозамкнутого четвертьволнового отрезка

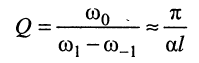
может достигать нескольких тысяч, что по крайней мере на порядок выше добротности, достижимой в RLC-KOHTypax.

Линейный вольтметр

Определение:

Линейным вольтметром (рис. 25.12) называется измерительный прибор с малым входным сопротивлением , включённый через четвертьволновый отрезок линии.

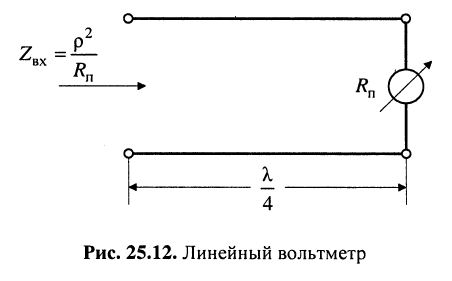
Подключение измерительного прибора к четвертьволновому отрезку образует практически короткозамкнутый отрезок, входное сопротивление которого (а потому и самого линейного вольтметра) становится очень большим. Такой прибор не оказывает заметного влияния на режим работы линии, а потому и на результаты измерений напряжения.

Действующие значения тока 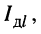протекающего через измерительный прибор, и напряжения  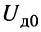подведённого к линейному вольтметру, связаны соотношением 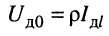, что следует из уравнений (25.8) при  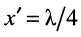Подобные приборы используются в технике СВЧ.

Трансформатор сопротивлений

В технике СВЧ типовым является каскадное включение линий, имеющих разные волновые сопротивления 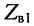и 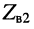(рис. 25.13). В связи с этим возникает задача согласования сопротивлений таких линий, т. е. преобразование, или трансформация указанных сопротивлений.

Для этого между двумя линиями включают согласующий трансформатор сопротивлений, представляющий собой четвертьволновый отрезок. Найдём, чему должно быть равно волновое сопротивление этого отрезка. Воспользуемся уравнениями передачи линии в форме (25.2) при условии, что 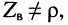, и запишем их для отрезка длиной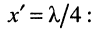

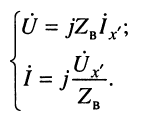
Отсюда имеем входное

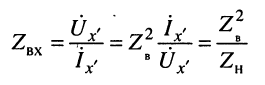
и волновое

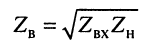
сопротивления отрезка.

Но входное сопротивление отрезка равно волновому сопротивлению левой линии 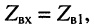 а сопротивление его нагрузки равно волновому сопротивлению правой линии 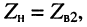поэтому волновое сопротивление отрезка равно корню квадратному из произведения волновых сопротивлений каскадно включаемых линий:

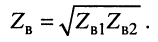
Четверть и полуволновые отрезки длинных линий применяются в теории и практике волновых аналоговых фильтров, рассматриваемых в лекции 45.