Классический метод расчета переходных процессов

Содержание:

Классический метод расчета переходных процессов:

В работе электрических цепей различают два режима процессов: переходный и установившийся.

Переходной процесс

Переходным процессом в электрической цепи называют электромагнитный процесс, возникающий в цепи при переходе от одного установившегося режима к другому. Этот процесс возникает в электрических цепях при подключении к ним или отключении от них источников электрической энергии, а также при скачкообразном изменении схемы цепи или параметров входящих в нее элементов. Установившимся называют такой режим, при котором токи, напряжения и ЭДС в цепи являются постоянными функциями времени [I4].

В цепях, не содержащих энергоемких элементов (индуктивностей и емкостей), новый установившийся режим наступает непосредственно за моментом коммутации. Поэтому можно считать, что в таких цепях переходные процессы отсутствуют.

В цепях с энергоемкими элементами переходные процессы продолжаются некоторое время, так как энергии электрических полей конденсаторов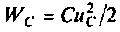

При анализе переходных процессов в электрических цепях классическим методом составляется система уравнений для мгновенных значений токов и напряжений. Эти уравнения составляются непосредственно по законам Кирхгофа или с помощью других методов расчет цепей, например метода контурных токов или метода узловых потенциалов. При этом используются соотношения между токами и напряжениями в элементах цепи

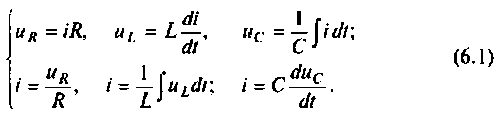
В полученной таким образом системе уравнений выбирается основная переменная, и исключением других переменных из системы уравнений получают одно уравнение, содержащее только основную переменную. В общем случае для линейных электрических цепей с сосредоточенными параметрами, содержащих элементы 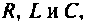 это уравнение является интегро-дифференциальным. Путем повторного дифференцирования этого уравнения можно получить линейное неоднородное уравнение с постоянными коэффициентами, имеющее в общем случае вид

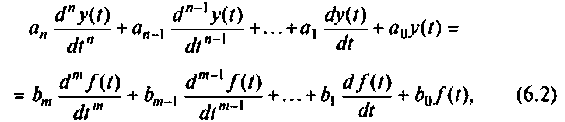
где 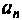— постоянные коэффициенты, зависящие от схемы цепи и параметров ее элементов; 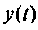— выходная величина (ток или напряжение); 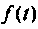— внешнее воздействие на цепь (источник ЭДС или тока).

Порядок высшей производной дифференциального уравнения определяет порядок цепи. Так, например, если этот порядок будет первым, то и цепь называют цепью первого порядка и т. д.

Решение уравнения (6.2) ищется в виде

где 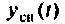— свободная составляющая, являющаяся общим решением однородного дифференциального уравнения

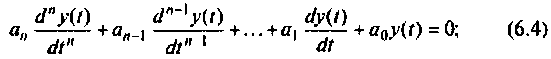
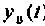— вынужденная составляющая, являющаяся частным решением уравнения (6.2).

Свободная составляющая 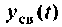— это свободные электрические токи или напряжения, которые равны разности переходных и установившихся токов или напряжений. Они характеризуют процесс рассеивания или накапливания энергии энергоемкими элементами L и С.

Вынужденная составляющая 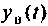 характеризует процесс, возникающий в цепи под влиянием внешнего воздействия 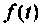после окончания переходного процесса. Это установившиеся, т.е. постоянные или периодические, токи и напряжения, которые устанавливаются в электрической цепи после окончания переходных процессов при воздействии на цепь постоянных или периодических ЭДС или токов.

Решение однородного дифференциального уравнения имеет вид

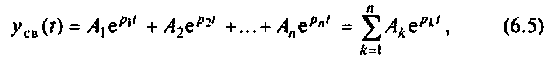
где 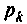— корни характеристического уравнения

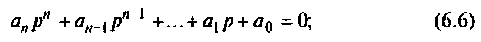
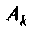— постоянная интегрирования.

Корни характеристического уравнения 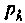у пассивных электрических цепей всегда либо вещественные отрицательные, либо комплексные сопряженные с отрицательной вещественной частью. Характер корней уравнения определяет вид свободной составляющей (табл. 6.1).

Особенностью метода является необходимость определения постоянных интегрирования и корней характеристического уравнения.

Число постоянных интегрирования и корней характеристического уравнения зависит от порядка цепи. Постоянные интегрирования находят из начальных условий искомой функции и ее производных.

Законы коммутации

Начальные условия — значения токов и напряжений при t = 0.

Независимые начальные условия - это величины, которые согласно законам коммутации не изменяются скачком. Они определяются из расчета установившегося режима до коммутации:

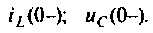
Зависимые начальные условия — это значения токов и напряжений в момент коммутации 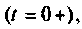 которые изменяются скачком. Они определяются по схеме, образованной после коммутации, по законам Кирхгофа с учетом законов коммутации.

Пример расчета начальных условий

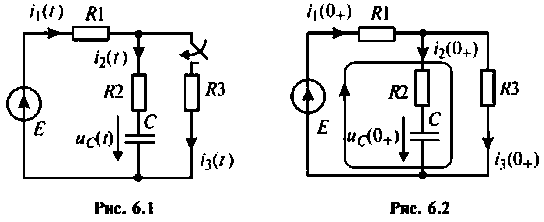
Независимые начальные условия (рис. 6.1) определяют по второму закону коммутации, используя соотношение (6.2)

Зависимые начальные условия находят для после коммутационной схемы (рис. 6.2), записав уравнения в соответствии с законами Кирхгофа с учетом того, что 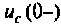известно, т. е.:

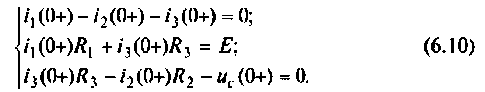
Выразим из первого уравнения системы уравнений (6.10) 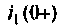и подставим во второе уравнение.

Тогда

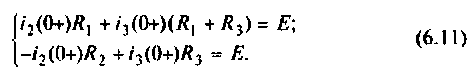
В матричной форме система уравнений (6.11) принимает вид:

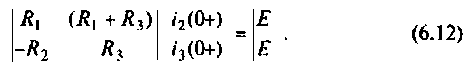
Решении системы уравнений (6.12), согласно формулам Крамера имеют вид:

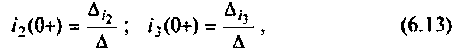
где

 

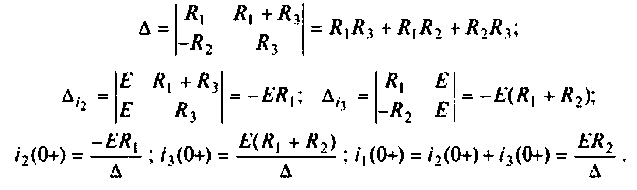
Определение корней характеристического уравнения

Определение корней по однородному уравнению:

Записывают неоднородное дифференциальное уравнение относительно тока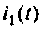

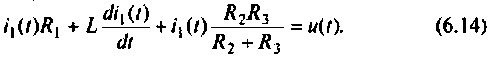
Преобразуя однородное уравнение, получают характеристическое

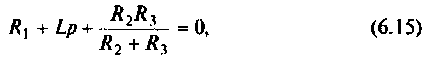
откуда корень характеристического уравнения

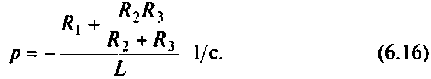
Определение корней по входному комплексному сопротивлению после коммутационной схемы

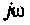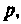Запишем выражение для входною комплексного сопротивления, приравняем его к нулю (для схемы с источником ЭДС) или комплексную проводимость (для схемы с источником тока)  заменив на  из уравнения  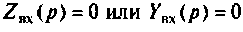определяют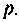

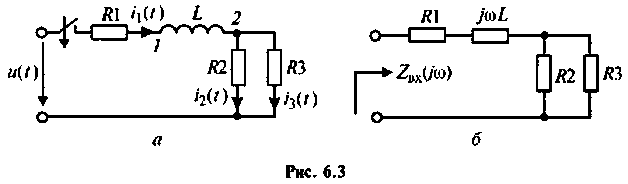
Переходя от исследуемой схемы (рис. 6.3, a) к комплексной схеме замещения {рис. 6.3, б), определяют

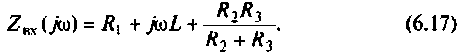
Заменив 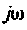на 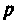и приравняв 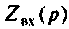к нулю, получим

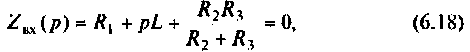
откуда корень полученного уравнения

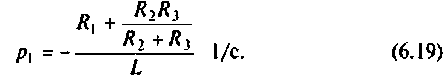
Определение корней по постоянной времени цепи

Известно [4, 14], что 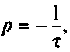 где — постоянная времени цепи.

Для цепи с одним индуктивным элементом постоянная времени 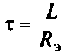, а с емкостным —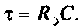

Для определения 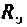необходимо закоротить входной источник ЭДС или разорвать ветвь с источником тока в после коммутационной схеме (см. рис. 6.3, а) и определить общее сопротивление цепи относительно зажимов peактивного элемента (рис. 6.4):

     

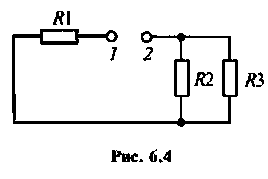
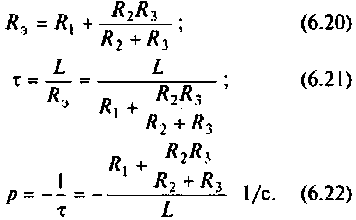
Для последовательного колебательного контура

Определение корней по определителю матрицы комплексных контурных сопротивлений (узловых проводимостей)

Определитель матрицы комплексных контурных сопротивлений (узловых проводимостей) приравнивают к нулю и, заменив 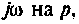рассчитывают корни уравнений 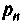(см. рис. 6.3, б):

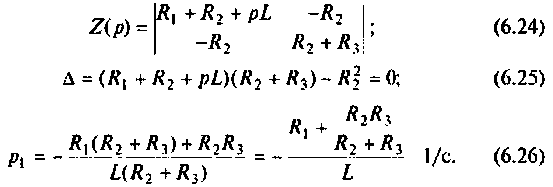
Порядок расчета переходных процессов. Составляют дифференциальные уравнения для послекоммутационной схемы относительно величин, которые согласно законам коммутации не изменяются скачком. Решение уравнений представляют в виде суммы вынужденной 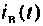и свободной 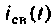составляющих:

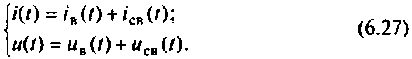
Определяют вынужденную составляющую тока (напряжения), используя методы расчета цепи в установившемся режиме, т.е. в цепи после окончания переходного процесса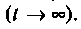

Определяют свободную составляющую.

Вычисляют постоянные интегрирования.

Рассчитывают корни характеристического уравнения р„.

Записывают решение, строят графики.

Проверяют решение, изображают схему при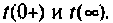

Качественный анализ переходных процессов

В цепях с одним реактивным элементом можно провести качественный анализ переходных процессов без составления и решения дифференциальных уравнений, применив законы Кирхгофа и учитывая законы коммутации. Для этого используют два положения:

1. в цепях 1-го порядка свободная составляющая затухает но экспоненциальному закону ;
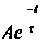2. закон изменения вынужденной составляющей определяется характером воздействующих на цепь напряжений.

Порядок расчета переходных процессов в цепях первого порядка:

• определяют значения переходных токов и напряжений для
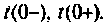
• определяют значения переходных токов и напряжений для 
• определяют постоянную времени цепи
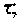
• строят графики токов и напряжений;
• записывают по графикам аналитическое выражение для переходных токов и напряжений.

Примеры решения типовых задач

Пример 6.5.1.

Накопительная емкость импульсного модулятора передающего устройства РЛС (рис. 6.5) после включения разряжается через разрядное сопротивление. Определить время, через которое напряжение на емкости уменьшится до уровня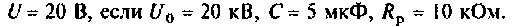

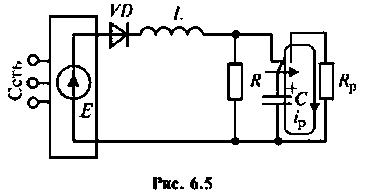
Решение

Составляют дифференциальное уравнение для послекоммутационной схемы относительно напряжения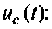


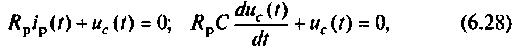
где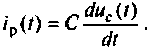 

Решением дифференциального уравнения служит напряжение на емкости в переходном и установившемся режимах и имеет вид

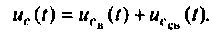
Вынужденная составляющая напряжения (в послекоммутационной схеме при )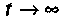

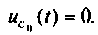
Свободная составляющая напряжения 

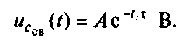
Рассчитывают постоянную интегрирования А из начальных условий |при /(0+)].

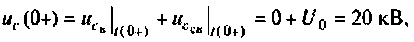
откуда

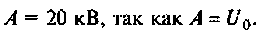
Определяют постоянную времени, используя соотношение 

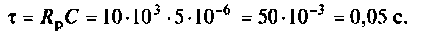
Находят напряжение в переходном режиме

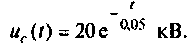
Вычисляют время разряда накопительной емкости из уравнений

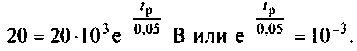
После логарифмирования получаем:

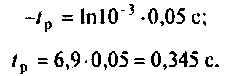
Строят, например, в среде Mathcad, графики изменения напряжения на емкости в переходном режиме (рис. 6.6).

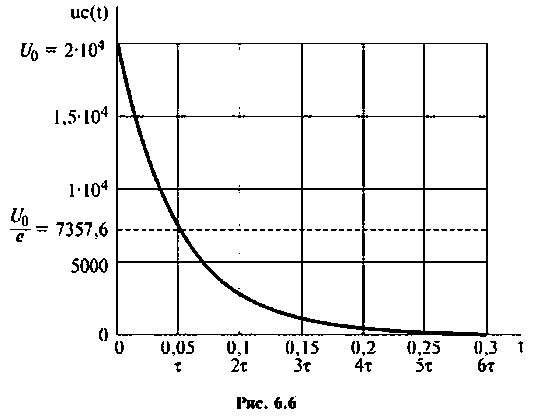
Определяют длительность переходного процесса

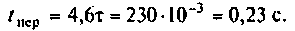
Вывод. Для регулирования длительности переходного процесса необходимо изменять в цепи постоянную времени 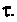Это достигается путем выбора параметров R и С. За время 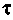свободная составляющая уменьшается в е = 2,718 раз.

Пример 6.5.2.

Обмотка электромагнитного реле подключается к источнику постоянной ЭДС 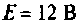последовательно с добавочным сопротивлением 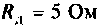(рис. 6.7).

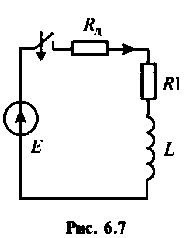
Найти время, через которое срабатывает реле, если ток срабатывания 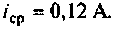 Параметры обмотки реле: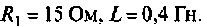

Решение

Составляют дифференциальное уравнение для послекоммутационной схемы относительно тока

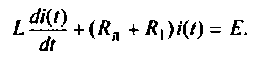
Решив полученное дифференциальное уравнение, получают ток переходного процесса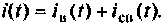

Определяют вынужденную составляющую тока (в послекоммутационной схеме при )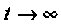

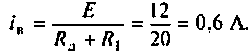
Определяет свободную составляющую тока

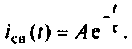
Определяют постоянную интегрирования А из начальных условий. Независимые начальные условия находят по первому закону коммутации

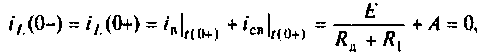
откуда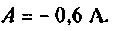

Определяют постоянную времени электрической цепи

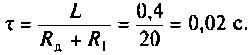
Определяют ток в переходном режиме

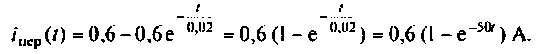
Определяют время срабатывания реле из уравнения

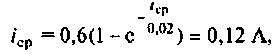
в результате следующих преобразований которого

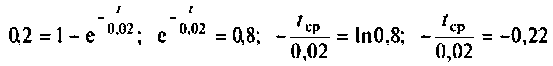
получаем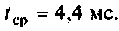

В среде Mathcad график функции i(t) имеет вид, приведенный на рис. 6.8.

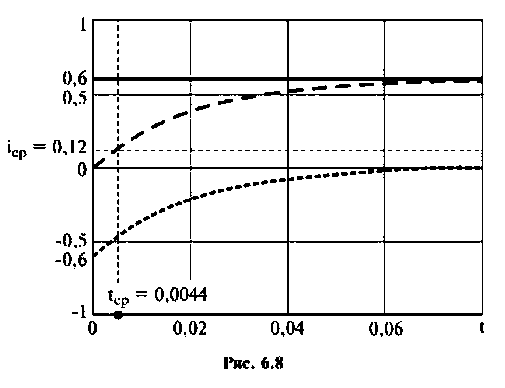
Выводы. 1. Подбирая различное по значению добавочное сопротивление 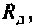можно управлять временем срабатывания реле.

2.Приведенный порядок расчета можно применить в интегрирующих и дифференцирующих цепях, используемых для коррекции динамических свойств систем автоматического управления.

Пример 6.5.3.

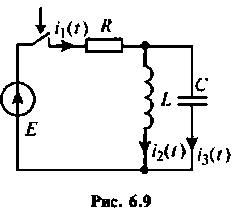
Параллельный колебательный контур (рис. 6.9) подключается к источнику ЭДС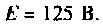

Определить закон изменения напряжении 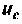для трех случаев: 

  

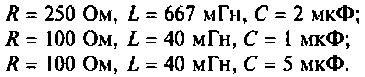
Решение

Определяют напряжение на конденсаторе в переходном режиме как сумму вынужденной и свободной составляющей

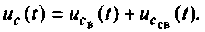
Определяют вынужденную составляющую напряжения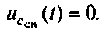 

При установившемся режиме 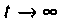конденсатор шунтирован катушкой индуктивности накоротко.

Определяют корни характеристического уравнения 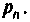Для этого находят входное сопротивление цепи и приравнивают к нулю (см. разд. 6.4.2)

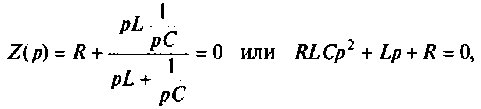
откуда

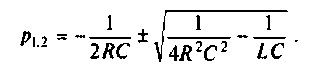
Для трех заданных значений параметров определяют вид корней:

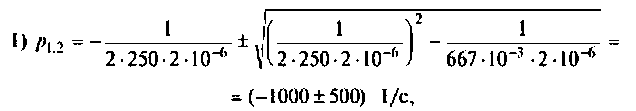
а после вычислений получаем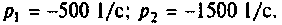

Корни действительные и различные, поэтому свободная составляющая напряжения на конденсаторе имеет вид

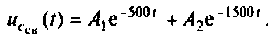
2)    

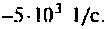
Корни действительные, равные, следовательно,

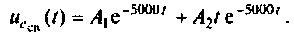
3)

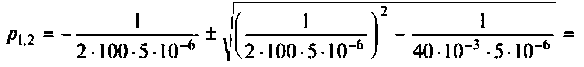
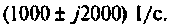
Корни комплексные, сопряженные, тогда

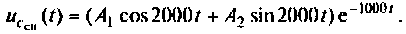
Определяют постоянные интегрирования 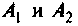из начальных условий:

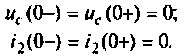
Решают уравнения, составленные по законам Кирхгофа для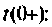 

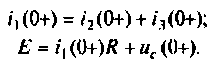
Далее находят 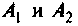из выражений для  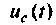и 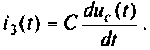 Для момента времени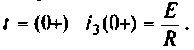

Рассчитаем 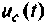для трех случаев корней:

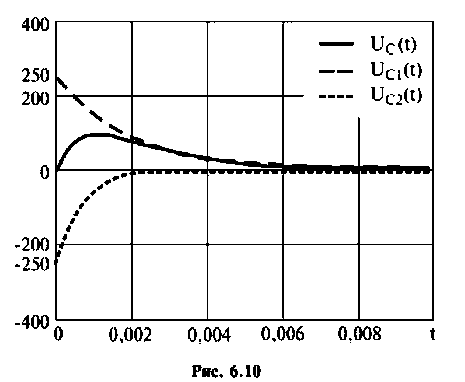
1) корни действительные и различные (рис. 6.10): 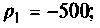 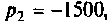тогда

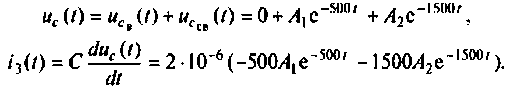
При t = (0+)

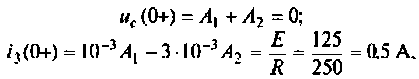
отсюда

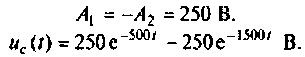
Графики напряжения 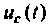и его составляющих выполнены в среде Mathcad и показаны на рис. 6.10;

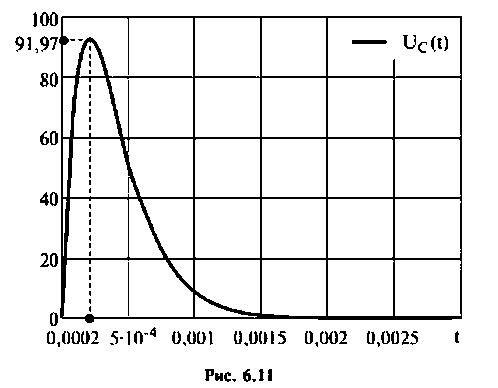
2) корни действительные и равные (рис. 6.11): 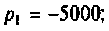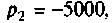тогда

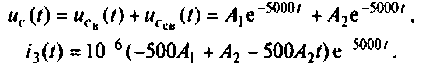
При t = (0+)

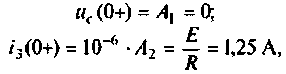
отсюда

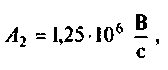
тогда

.

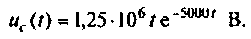Компьютерный график напряжения 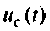приведен на рис. 6.11;

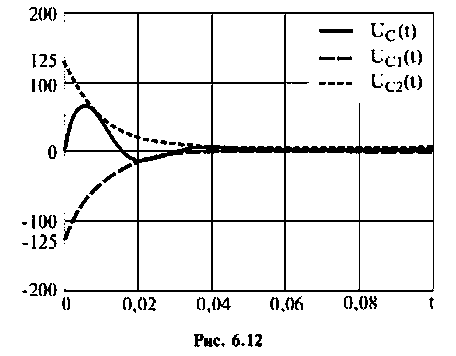
3) корни комплексные, сопряженные (рис. 6.12): 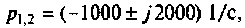тогда

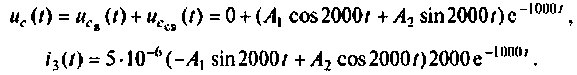
 При t=(0+) 

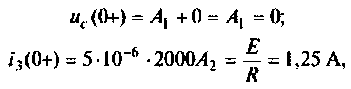
отсюда

 

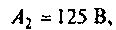
тогда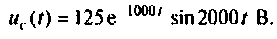   

Компьютерный график напряжения 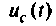приведен на рис. 6.12.

Выводы

1. Напряжение 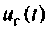при колебательном режиме, если  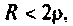представляет собой затухающее колебание. Уменьшение R приводит к увеличению времени

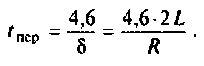
2. Переходной процесс в параллельном колебательном контуре при R < 2р используют в автоколебательных системах, где контур является нагрузочной цепью.

Пример 6.5.4. Интегрирующая цепь (рис. 6.13) с параметрами 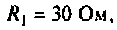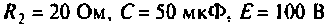подключается к сопротивлению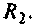 

Произвести качественный анализ изменении напряжения на конденсаторе и токов в ветвях в переходном режиме.

Решение

Определяют значение переходных токов и напряжений для 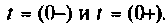Из эквивалентной схемы для 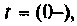приведенной на рис. 6.14, находят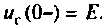

Эквивалентная схема для 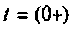прицелена на рис. 6.15.

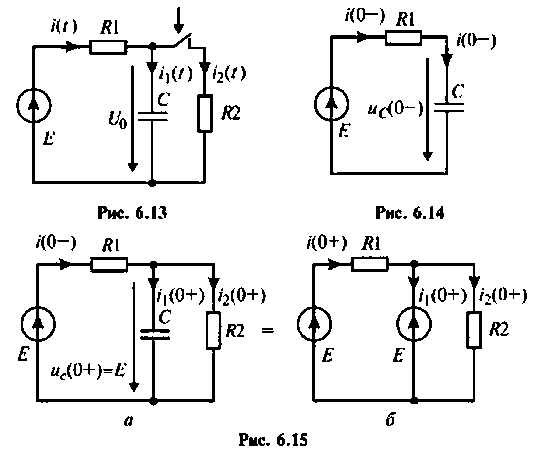
Для этой схемы составляют систему уравнений по законам Кирхгофа:

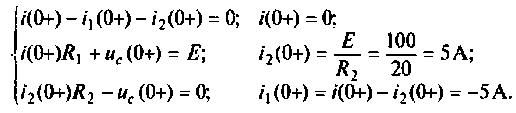
Определяют значение переходных токов и напряжений для 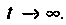Эквивалентная схема для 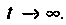приведена на рис. 6.16.

           

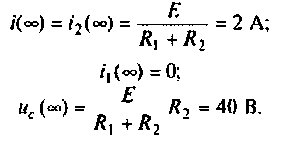
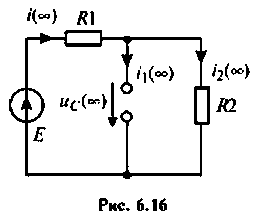
Определяют 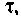используя соотношение (6.21)

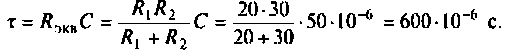
Записывают аналитические выражения для переходных токов и напряжений:

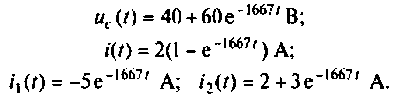
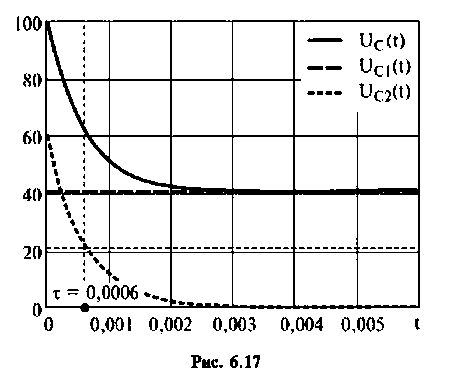
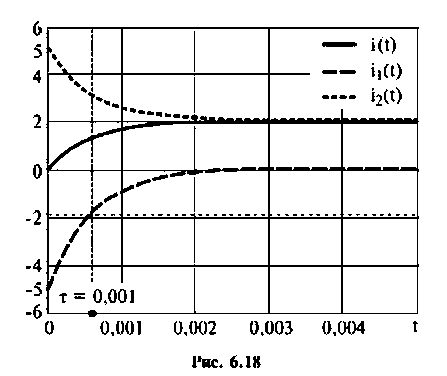
Строят графики напряжений и токов, например, в среде Mathcad (рис. 6.17, 6.18).

Цепи в виде резисторно-конденсаторного делителя нашли широкое применение и импульсных устройствах РЭТ.