
Кинематика сплошной среды в теоретической механике
Содержание:
Основы кинематики сплошной среды:
Сплошной средой считают деформируемые тела, различные жидкости, не очень разреженные газы. Понятия скорости и ускорения точки сплошной среды такие же, как и в кинематике одной точки. В кинематике сплошной среды роль точки отводится малой частице этой среды. Рассмотрим задания движения сплошной среды и получим формулы, по которым вычисляются скорости и ускорения точек сплошной среды.
Движение сплошной среды может быть изучено двумя методами, один из которых — метод Лагранжа — является обобщением метода, применявшегося в кинематике одной точки. Движение в методе Лагранжа задается в переменных Лагранжа. Другой метод — метод Эйлера — широко использует концепцию теории поля. При этом движение задается и изучается в переменных Эйлера. При рассмотрении движения сплошной среды преимущественно используется полевой подход, базирующийся на методе Эйлера и соответственно использующий переменные Эйлера.
Переменные Лагранжа
В выделенном объеме сплошной среды каждая его точка (малая частица) в фиксированный момент времени, например 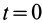
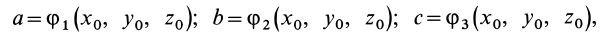
допускающими вторые производные по всем переменным. Параметры 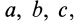 так же как и
так же как и 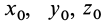 дают возможность отличать одну точку сплошной среды от другой. В разные моменты времени
дают возможность отличать одну точку сплошной среды от другой. В разные моменты времени 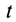 различные точки сплошной среды характеризуются четырьмя независимыми переменными
различные точки сплошной среды характеризуются четырьмя независимыми переменными 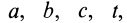 которые называются переменными Лагранжа.
которые называются переменными Лагранжа.
Для задания движения сплошной среды в переменных Лагранжа, как и в случае одной точки, достаточно задать декартовы координаты 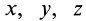 всех точек сплошной среды или их радиусы-векторы
всех точек сплошной среды или их радиусы-векторы 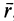 , но уже как функции четырех переменных Лагранжа:
, но уже как функции четырех переменных Лагранжа:
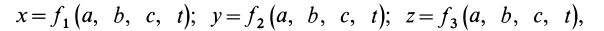
или
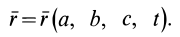
В кинематике одной точки, которая рассматривалась ранее, использовались переменные Лагранжа для этой точки. Параметры 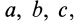 не применялись, так как не было других точек, от которых следовало отличать рассматриваемую точку. Оставалась зависимость координат точки или ее радиуса-вектора только от времени. Для сплошной среды задание параметров
не применялись, так как не было других точек, от которых следовало отличать рассматриваемую точку. Оставалась зависимость координат точки или ее радиуса-вектора только от времени. Для сплошной среды задание параметров 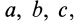 позволяет выделить конкретную точку. Разным значениям этих параметров соответствуют различные точки сплошной среды.
позволяет выделить конкретную точку. Разным значениям этих параметров соответствуют различные точки сплошной среды.
Если движение сплошной среды задано в переменных Лагранжа, то скорости и ускорения в этих переменных определяются по обычным формулам кинематики точки:
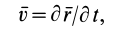
или
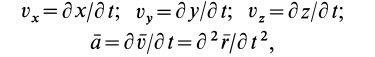
или
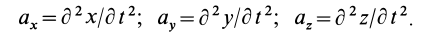
Производные по времени 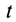 частные, так как вычисляются при фиксированных значениях переменных
частные, так как вычисляются при фиксированных значениях переменных 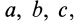 . Величины
. Величины 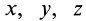 или
или 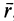 можно также дифференцировать по каждому из переменных
можно также дифференцировать по каждому из переменных  .
.
В методе Лагранжа объектом изучения являются сами точки движущейся сплошной среды.
Переменные Эйлера
В механике сплошной среды, особенно для жидкостей и газов, а также в теории поля преимущественно используются метод Эйлера и соответственно переменные Эйлера. В методе Эйлера рассматриваются не фиксированные точки сплошной среды, а точки пространства, занятые движущейся сплошной средой. За независимые переменные принимают время 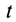 и декартовы координаты точки
и декартовы координаты точки 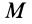 пространства
пространства 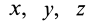 или другие параметры, характеризующие различные точки пространства. Четыре независимые переменные величины
или другие параметры, характеризующие различные точки пространства. Четыре независимые переменные величины 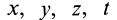 называют переменными Эйлера.
называют переменными Эйлера.
Различные векторные и скалярные величины, характеризующие сплошную среду, такие, как, например, скорость, ускорение, плотность и т. п., рассматривают как функции этих переменных. В случае сплошной среды изучаются поля скалярных и векторных величин, характеризующих движущуюся сплошную среду и ее свойства. Изучаются распределение этих величин по точкам пространства, занятого сплошной средой, и их изменение с течением времени.
По известному векторному полю скоростей сплошной среды, заданному в переменных Эйлера 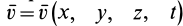 , можно определить векторное поле ускорений
, можно определить векторное поле ускорений 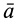 в этих переменных. Получим соответствующую формулу. Движение сплошной среды в переменных Эйлера считается известным, если задано поле скоростей в этих переменных. Согласно определению ускорения точки сплошной среды, находящейся в какой-либо точке пространства
в этих переменных. Получим соответствующую формулу. Движение сплошной среды в переменных Эйлера считается известным, если задано поле скоростей в этих переменных. Согласно определению ускорения точки сплошной среды, находящейся в какой-либо точке пространства 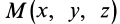 в момент времени
в момент времени 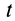 , следует рассмотреть положение этой точки сплошной среды в момент времени
, следует рассмотреть положение этой точки сплошной среды в момент времени 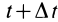 . Она в этот момент вследствие движения сплошной среды окажется в другой точке пространства
. Она в этот момент вследствие движения сплошной среды окажется в другой точке пространства 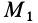 с координатами
с координатами 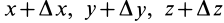 и будет иметь скорость
и будет иметь скорость 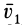 , зависящую от координат этой новой точки пространства
, зависящую от координат этой новой точки пространства 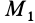 и времени
и времени 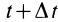 . Изменение координат рассматриваемой точки сплошной среды на
. Изменение координат рассматриваемой точки сплошной среды на 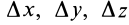 произошло вследствие изменения времени на
произошло вследствие изменения времени на 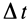 , поэтому
, поэтому
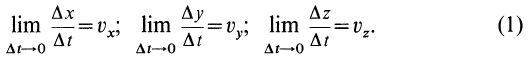
Разложим скорость 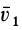 в ряд по степеням величин
в ряд по степеням величин 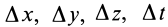 :
:
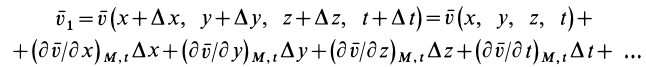
Индексы 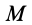 и
и 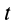 у производных указывают на то, что они берутся в точке
у производных указывают на то, что они берутся в точке 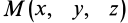 пространства в момент времени
пространства в момент времени 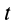 . Согласно определению ускорения
. Согласно определению ускорения 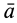 точки сплошной среды, находящейся в точке пространства
точки сплошной среды, находящейся в точке пространства 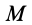 в момент времени
в момент времени 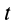 , имеем
, имеем
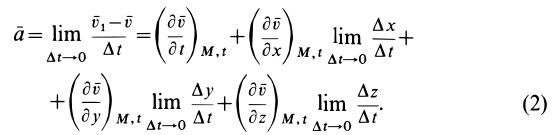
Остальные слагаемые ряда в пределе обращаются в ноль. Подставляя (1) в (2) и опуская для краткости индексы 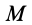 и
и 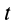 у производных, получаем
у производных, получаем
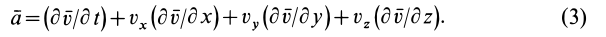
В проекциях на координатные оси имеем
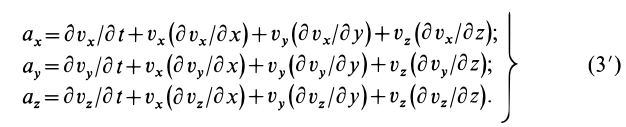
По векторной формуле (3) вычисляют поле ускорений в переменных Эйлера, если известно поле скоростей. В эту формулу входят 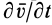 — локальная производная от вектора скорости — и группа слагаемых
— локальная производная от вектора скорости — и группа слагаемых 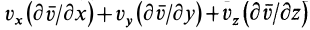 , представляющая собой конвективную производную от этого вектора. Полное изменение вектора скорости с течением времени, т. е. ускорение, обозначим
, представляющая собой конвективную производную от этого вектора. Полное изменение вектора скорости с течением времени, т. е. ускорение, обозначим 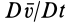 .
.
Локальная производная 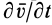 характеризует изменение вектора скорости v в точке
характеризует изменение вектора скорости v в точке 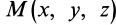 пространства вследствие изменения только одного времени при неизменных
пространства вследствие изменения только одного времени при неизменных 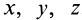 . Полная производная
. Полная производная 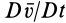 равна локальной производной
равна локальной производной 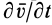 в тех точках пространства, в которых скорость в рассматриваемый момент времени равна нулю.
в тех точках пространства, в которых скорость в рассматриваемый момент времени равна нулю.
Группа слагаемых, представляющая конвективную производную, учитывает изменение вектора скорости, вызванное переносом рассматриваемой точки сплошной среды самой движущейся средой.
Рассмотрим частные случаи
1. Если 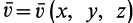 , т. е. поле скоростей стационарно, то
, т. е. поле скоростей стационарно, то 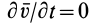 и
и 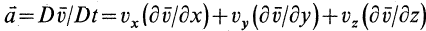 .
.
2. При 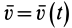
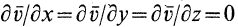 и
и 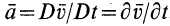 .
.
3. Если 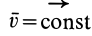 , то
, то 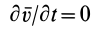 ,
, 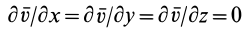 и
и 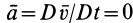 .
.
По формуле (3) вычисляют полные, или субстанциальные, производные по времени в переменных Эйлера от любых векторных или скалярных величин, характеризующих сплошную среду. Пусть, например, известно скалярное поле плотностей 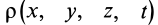 сплошной среды. Рассуждения, аналогичные приведенным при выводе формулы для ускорения, приведут к полной производной от
сплошной среды. Рассуждения, аналогичные приведенным при выводе формулы для ускорения, приведут к полной производной от 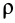 по времени
по времени 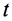
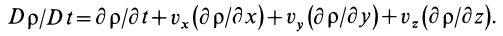
Если сплошная среда неподвижна, т. е. 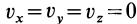 , то полная производная по времени от любой векторной или скалярной функции, характеризующей сплошную среду, согласно (3), равна локальной производной.
, то полная производная по времени от любой векторной или скалярной функции, характеризующей сплошную среду, согласно (3), равна локальной производной.
Преобразованием конвективной производной из (3) можно получить другое выражение для ускорения (формула Лэмба — Громеко):
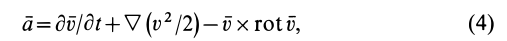
где 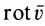 — вихрь вектора скорости, а
— вихрь вектора скорости, а  — символический оператор Гамильтона:
— символический оператор Гамильтона:
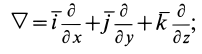
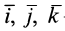 — единичные векторы, направленные по осям декартовой системы осей координат. Вихрь вектора скорости определяется выражением
— единичные векторы, направленные по осям декартовой системы осей координат. Вихрь вектора скорости определяется выражением
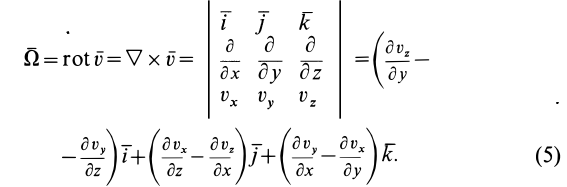
В дальнейшем используется также вектор 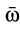 , определяемый как половина вихря вектора скорости:
, определяемый как половина вихря вектора скорости:

В проекциях на оси координат
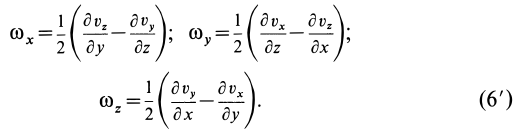
Для выяснения физического смысла 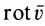 рассмотрим несколько примеров вычисления его по заданному полю скоростей.
рассмотрим несколько примеров вычисления его по заданному полю скоростей.
Пример 1.
Сплошная среда совершает плоское движение, параллельное оси 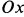 , с постоянной скоростью
, с постоянной скоростью 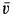 (рис. 104). Имеем
(рис. 104). Имеем 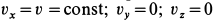 .
.
По формуле (5) для вектора вихря 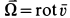 имеем:
имеем:
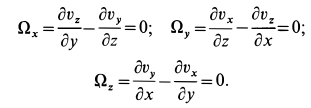
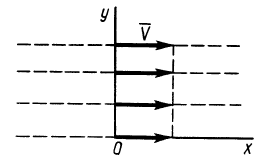
Рис. 104
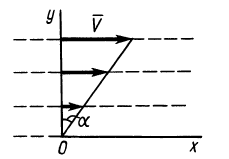
Рис. 105
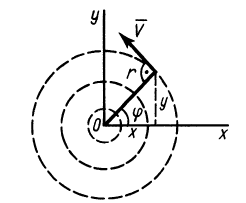
Рис. 106
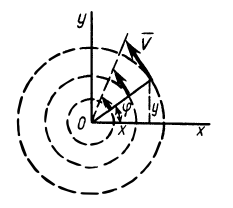
Рис. 107
Следовательно, 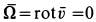 во всех точках пространства, занятого движущейся сплошной средой.
во всех точках пространства, занятого движущейся сплошной средой.
Пример 2.
Сплошная среда совершает плоское движение, параллельное оси 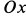 , со скоростью, распределенной по линейному закону (рис. 105). Траектории точек сплошной среды являются прямыми линиями, параллельными оси
, со скоростью, распределенной по линейному закону (рис. 105). Траектории точек сплошной среды являются прямыми линиями, параллельными оси 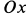 . В этом случае
. В этом случае
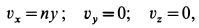
где 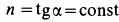 . Имеем:
. Имеем:
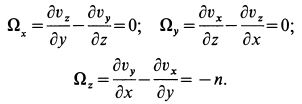
Таким образом, во всех точках потока сплошной среды
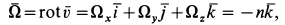
где 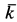 — единичный вектор, направленный по оси
— единичный вектор, направленный по оси 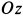 .
.
Пример 3.
Точки сплошной среды движутся по круговым траекториям с центрами на оси 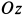 и скоростями, обратно пропорциональными радиусам окружностей (рис. 106), т.е.
и скоростями, обратно пропорциональными радиусам окружностей (рис. 106), т.е. 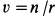 , где
, где 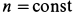 . Имеем:
. Имеем:
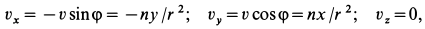
так как
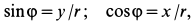
где 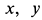 — координаты точки. По формуле (5) имеем
— координаты точки. По формуле (5) имеем
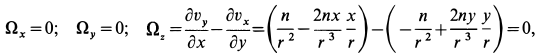
так как 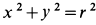 .
.
Следовательно,  во всех точках потока, кроме точки
во всех точках потока, кроме точки 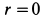 , для которой вычисления непригодны, так как в этой точке скорость обращается в бесконечность.
, для которой вычисления непригодны, так как в этой точке скорость обращается в бесконечность.
Пример 4.
Сплошная среда вращается как твердое тело вокруг неподвижной оси 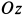 с угловой скоростью
с угловой скоростью 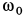 . Скорости точек сплошной среды в этом случае распределены по линейному закону (рис. 107), т. е.
. Скорости точек сплошной среды в этом случае распределены по линейному закону (рис. 107), т. е. 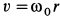 . В этом случае
. В этом случае
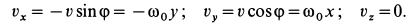
По формулам для вихря скорости имеем
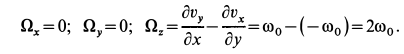
Следовательно,
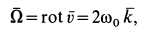
де 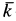 — единичный вектор, направленный по оси
— единичный вектор, направленный по оси 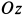 . Во всех точках потока
. Во всех точках потока  имеет постоянную величину и постоянное направление, параллельное оси
имеет постоянную величину и постоянное направление, параллельное оси 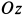 , в том числе и в точке
, в том числе и в точке  , где
, где 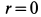 и
и 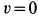 .
.
Угловая скорость
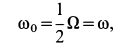
т. е. равна половине вихря вектора скорости. Таким образом, половина вихря вектора скорости является вектором угловой скорости вращения твердого тела вокруг неподвижной оси.
Распределение скоростей в малой окрестности точки пространства
Пусть известны скорость в точке  в момент
в момент 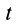 и производные от нее по координатам в этот же момент времени (рис. 108). Получим формулу для вычисления скорости в этот же момент времени в любой другой точке
и производные от нее по координатам в этот же момент времени (рис. 108). Получим формулу для вычисления скорости в этот же момент времени в любой другой точке 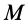 из малой окрестности точки
из малой окрестности точки  . Так как скорости в точках
. Так как скорости в точках 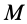 и
и  рассматриваются в один и тот же момент времени, то удобно выбрать начало осей координат, относительно которых изучается движение сплошной среды, в точке
рассматриваются в один и тот же момент времени, то удобно выбрать начало осей координат, относительно которых изучается движение сплошной среды, в точке  .
.
Точки 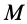 пространства из малой окрестности точки
пространства из малой окрестности точки  отличаются друг от друга только координатами
отличаются друг от друга только координатами 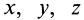 или радиусом-вектором
или радиусом-вектором 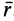 . Скорость в какой-либо точке
. Скорость в какой-либо точке 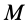 для фиксированного момента времени является функцией координат этой точки
для фиксированного момента времени является функцией координат этой точки 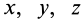 . Разложим
. Разложим 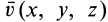 в степенной ряд по координатам х, у, z, ограничиваясь слагаемыми первой степени по этим переменным и пренебрегая слагаемыми второй и более высоких степеней, предполагая, что ими можно пренебречь по сравнению с сохраняемыми слагаемыми для достаточно малых
в степенной ряд по координатам х, у, z, ограничиваясь слагаемыми первой степени по этим переменным и пренебрегая слагаемыми второй и более высоких степеней, предполагая, что ими можно пренебречь по сравнению с сохраняемыми слагаемыми для достаточно малых 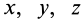 . Получим
. Получим
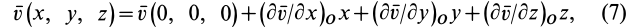
где 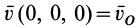 — скорость в точке
— скорость в точке  . Индекс
. Индекс  у производных служит указанием на то, что они вычисляются в точке
у производных служит указанием на то, что они вычисляются в точке  пространства. В дальнейшем его будем опускать. В проекциях на координатные оси из (7) имеем
пространства. В дальнейшем его будем опускать. В проекциях на координатные оси из (7) имеем
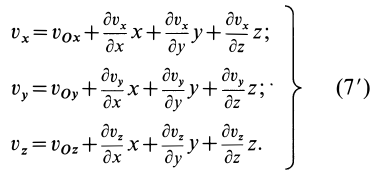
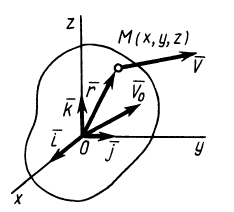
Рис. 108
Введем компоненты тензора скоростей деформации 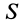 в точке
в точке  выражениями
выражениями
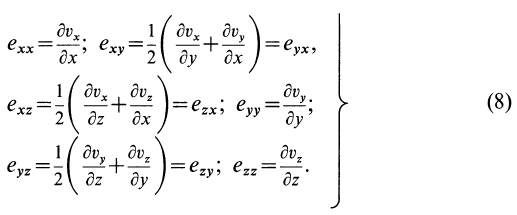
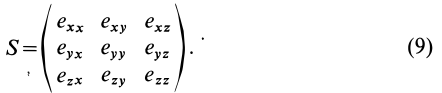
Тензор скоростей деформаций удобно представить в форме таблицы или матрицы:
Компоненты тензора скоростей деформаций, характеризующие движение сплошной среды, зависят от точки пространства и направления осей координат. Тензор 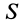 является симметричным тензором, так как согласно формулам, определяющим его компоненты,
является симметричным тензором, так как согласно формулам, определяющим его компоненты,
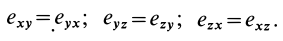
Для таких симметричных тензоров в линейной алгебре доказывается, что в каждой точке существуют такие прямоугольные оси координат, называемые главными осями, для которых тензор принимает диагональную форму:
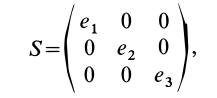
где 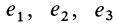 — компоненты тензора скоростей деформаций для главных осей. Известно также, что сумма диагональных компонентов является инвариантом. Она не изменяется при повороте осей координат в рассматриваемой точке, т. е.
— компоненты тензора скоростей деформаций для главных осей. Известно также, что сумма диагональных компонентов является инвариантом. Она не изменяется при повороте осей координат в рассматриваемой точке, т. е.
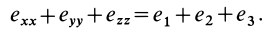
Скалярная величина
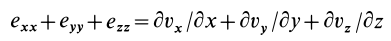
называется дивергенцией (расхождением) вектора скорости и обозначается 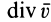 . Таким образом, по определению,
. Таким образом, по определению,
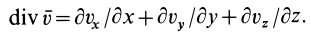
Величины 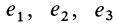 определяются из уравнения собственных значений тензора
определяются из уравнения собственных значений тензора 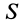 как его корни, т. е. как корни кубического уравнения для
как его корни, т. е. как корни кубического уравнения для 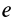 :
:
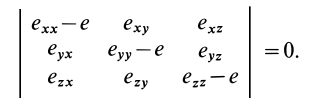
Известно, что числу соответствует геометрический образ, которым является точка на числовой оси. Вектору соответствует прямолинейный отрезок. Тензору 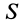 , компоненты которого имеют два индекса, можно поставить в соответствие поверхность второго порядка, которую называют эллипсоидом скоростей деформаций. Такие тензорные поверхности дальше будут рассмотрены для тензоров инерции и напряжений поверхностных сил.
, компоненты которого имеют два индекса, можно поставить в соответствие поверхность второго порядка, которую называют эллипсоидом скоростей деформаций. Такие тензорные поверхности дальше будут рассмотрены для тензоров инерции и напряжений поверхностных сил.
Применим для производных по координатам от проекций вектора скорости на оси координат тождественные преобразования Коши, прибавляя и вычитая одинаковые величины и используя (6') и (8). Имеем

Из (7') с учетом этих преобразований получаем
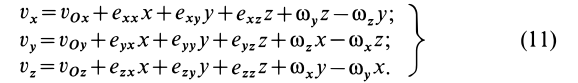
В векторной форме (11) примет вид

где 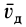 называется скоростью деформации. Проекции скорости деформации на оси координат определяют по формулам
называется скоростью деформации. Проекции скорости деформации на оси координат определяют по формулам
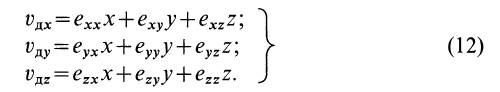
По формуле (11') вычисляется скорость в момент времени 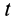 в любой точке
в любой точке 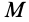 пространства из малой окрестности точки
пространства из малой окрестности точки 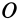 , если в этот же момент известны скорость, вихрь скорости и тензор скоростей деформаций
, если в этот же момент известны скорость, вихрь скорости и тензор скоростей деформаций 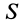 в точке
в точке 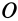 . Формула (11') является обобщением на случай сплошной среды формулы (21) (см. § 8 гл. 4) для скорости точки свободного твердого тела в общем случае его движения. Для твердого тела
. Формула (11') является обобщением на случай сплошной среды формулы (21) (см. § 8 гл. 4) для скорости точки свободного твердого тела в общем случае его движения. Для твердого тела 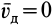 . Кроме того, для сплошной среды роль угловой скорости выполняет половина вихря вектора скорости в точке
. Кроме того, для сплошной среды роль угловой скорости выполняет половина вихря вектора скорости в точке  .
.
Рассмотрим скорость деформации 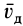 . Для простоты пусть мы выбрали такую точку
. Для простоты пусть мы выбрали такую точку  , в которой в рассматриваемый момент времени
, в которой в рассматриваемый момент времени 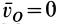 и
и 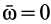 . Тогда для скорости в какой-либо точке
. Тогда для скорости в какой-либо точке 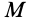 из малой окрестности этой точки, согласно (11'), имеем
из малой окрестности этой точки, согласно (11'), имеем

или в проекциях на оси координат
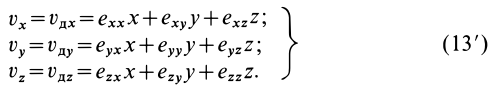
Если в точке 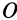
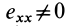 , а все остальные компоненты тензора скоростей деформаций равны нулю, то из (13') получаем:
, а все остальные компоненты тензора скоростей деформаций равны нулю, то из (13') получаем:
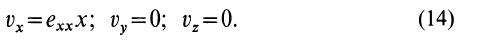
Из (14) следует, что точки сплошной среды из малой окрестности точки 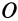 , находящейся в плоскости
, находящейся в плоскости 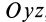 , имеют скорости, равные нулю, так как для них
, имеют скорости, равные нулю, так как для них 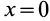 . Точки, расположенные в плоскости, параллельной этой координатной плоскости на расстоянии
. Точки, расположенные в плоскости, параллельной этой координатной плоскости на расстоянии 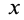 в положительном направлении оси
в положительном направлении оси 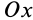 , имеют одинаковые скорости, пропорциональные
, имеют одинаковые скорости, пропорциональные 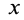 и направленные параллельно
и направленные параллельно 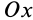 , если
, если 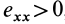 , и в обратную сторону, если
, и в обратную сторону, если 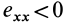 . Для точек плоскости, параллельной
. Для точек плоскости, параллельной 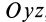 , но отстоящей от нее на
, но отстоящей от нее на 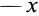 , скорости имеют противоположное направление. Таким образом,
, скорости имеют противоположное направление. Таким образом, 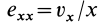 в малой окрестности точки
в малой окрестности точки 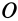 характеризует скорость расширения
характеризует скорость расширения 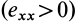 или сжатия
или сжатия 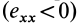 частицы сплошной среды, приходящуюся на единицу расстояния в направлении, параллельном оси
частицы сплошной среды, приходящуюся на единицу расстояния в направлении, параллельном оси 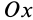 (рис. 109). Аналогично,
(рис. 109). Аналогично, 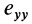 и
и 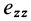 характеризуют относительные скорости растяжения или сжатия, приходящиеся на единицу расстояния в малой окрестности точки
характеризуют относительные скорости растяжения или сжатия, приходящиеся на единицу расстояния в малой окрестности точки 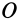 , в направлениях, параллельных осям координат
, в направлениях, параллельных осям координат 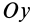 и
и 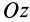 .
.
Допустим, что 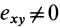 , а все остальные компоненты тензора скоростей деформации равны нулю. Тогда из (13') следует:
, а все остальные компоненты тензора скоростей деформации равны нулю. Тогда из (13') следует:
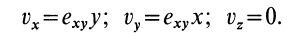
Рис. 109
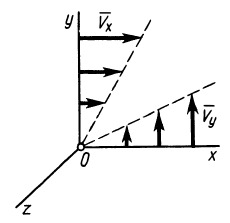
Рис. 110
Это показывает, что точки сплошной среды из малой окрестности точки 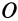 , расположенные в плоскости
, расположенные в плоскости 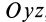 , в частности на оси
, в частности на оси 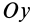 , для которых
, для которых 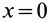 , имеют скорости, параллельные оси
, имеют скорости, параллельные оси 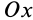 . Эти скорости распределены по линейному закону (рис. 110) и направлены в положительном направлении этой оси, если
. Эти скорости распределены по линейному закону (рис. 110) и направлены в положительном направлении этой оси, если 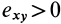 , и в обратную сторону, если
, и в обратную сторону, если 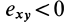 . Аналогично, точки, находящиеся в плоскости
. Аналогично, точки, находящиеся в плоскости 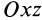 , в частности на оси
, в частности на оси 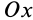 , имеют скорости, распределенные по линейному закону и параллельные оси
, имеют скорости, распределенные по линейному закону и параллельные оси 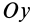 . Если
. Если 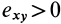 , то точки части сплошной среды из малой окрестности точки
, то точки части сплошной среды из малой окрестности точки 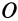 , находящиеся в момент времени
, находящиеся в момент времени 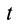 на осях координат
на осях координат 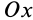 и
и 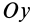 и образующих прямой угол, в следующий момент времени расположатся на прямых линиях, образующих острый угол. Если
и образующих прямой угол, в следующий момент времени расположатся на прямых линиях, образующих острый угол. Если 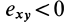 , то прямой угол превратится в тупой. Таким образом, величина
, то прямой угол превратится в тупой. Таким образом, величина 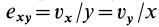 характеризует относительную скорость скоса углов в плоскости
характеризует относительную скорость скоса углов в плоскости 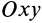 . Соответственно
. Соответственно 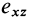 и
и 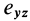 характеризуют относительные скорости скоса углов в плоскостях
характеризуют относительные скорости скоса углов в плоскостях 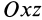 и
и 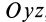 , приходящиеся на единицу длины.
, приходящиеся на единицу длины.
В общем случае, если все компоненты тензора скоростей деформации отличны от нуля, рассмотренные эффекты в окрестности точки  наложатся друг на друга. Так как точка
наложатся друг на друга. Так как точка  является произвольной точкой пространства, в котором движется сплошная среда, то все изложенное применимо для малой окрестности любой точки.
является произвольной точкой пространства, в котором движется сплошная среда, то все изложенное применимо для малой окрестности любой точки.
Линии и трубки тока
При рассмотрении движения сплошной среды и применении переменных Эйлера используется понятие линий тока, т. е. линий, в каждой точке которых в рассматриваемый момент времени векторы скоростей параллельны касательным этих линий. Если вектор в какой-либо точке линии тока направлен по касательной к этой линии, то, по определению линии тока, он должен быть параллельным вектору скорости 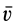 в этой точке. Два параллельных вектора отличаются друг от друга только скалярным множителем
в этой точке. Два параллельных вектора отличаются друг от друга только скалярным множителем 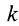 (положительным или отрицательным). Следовательно,
(положительным или отрицательным). Следовательно,

Рис. 111
Если проекции вектора 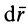 на оси координат есть
на оси координат есть 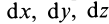 , то в проекциях на эти оси выражение (15) примет форму
, то в проекциях на эти оси выражение (15) примет форму
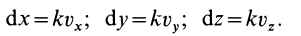
Отбрасывая произвольный множитель 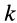 , эти уравнения можно представить в следующем виде:
, эти уравнения можно представить в следующем виде:
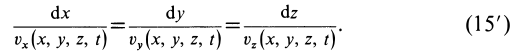
Два уравнения (15') относительно координат 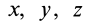 для фиксированного момента времени
для фиксированного момента времени 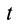 являются дифференциальными уравнениями семейства линий тока. После интегрирования этих уравнений появятся произвольные постоянные, различным значениям которых соответствуют разные линии тока. На фиксированной линии тока в рассматриваемый момент времени находятся разные точки сплошной среды в отличие от траекторий. Для стационарного движения, при котором вектор скорости не зависит от времени, семейство линий тока совпадает с семейством траекторий. Для нестационарного движения это разные семейства линий.
являются дифференциальными уравнениями семейства линий тока. После интегрирования этих уравнений появятся произвольные постоянные, различным значениям которых соответствуют разные линии тока. На фиксированной линии тока в рассматриваемый момент времени находятся разные точки сплошной среды в отличие от траекторий. Для стационарного движения, при котором вектор скорости не зависит от времени, семейство линий тока совпадает с семейством траекторий. Для нестационарного движения это разные семейства линий.
Линии тока являются векторными линиями для векторного поля скоростей точек сплошной среды. Аналогичные векторные линии можно получить для любого другого векторного поля, например векторного поля вихря вектора скорости и т. п.
Если выбрать в пространстве, в котором движется сплошная среда, какой-либо замкнутый контур 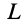 (рис. 111) и через каждую его точку провести свою линию тока, то получим трубку тока. Сплошная среда не может выходить из трубки тока через боковую ее поверхность, так как в ее точках, состоящих из линий тока, скорости точек сплошной среды направлены по касательным к поверхности трубки тока. Сплошная среда может входить и выходить из трубки тока только через ее торцовые сечения. Трубки тока используются для формулировки некоторых интегральных форм теорем о движении сплошной среды.
(рис. 111) и через каждую его точку провести свою линию тока, то получим трубку тока. Сплошная среда не может выходить из трубки тока через боковую ее поверхность, так как в ее точках, состоящих из линий тока, скорости точек сплошной среды направлены по касательным к поверхности трубки тока. Сплошная среда может входить и выходить из трубки тока только через ее торцовые сечения. Трубки тока используются для формулировки некоторых интегральных форм теорем о движении сплошной среды.
Поток и циркуляция вектора скорости
Поток вектора скорости: Выберем в пространстве, в котором движется сплошная среда, неподвижную поверхность относительно рассматриваемой системы отсчета. Разобьем ее на малые элементарные площадки с площадью 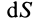 (рис. 112). Потоком вектора скорости
(рис. 112). Потоком вектора скорости 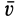 через элементарную площадку
через элементарную площадку 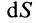 , определяемую внешней нормалью
, определяемую внешней нормалью 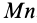 , называется скалярная величина
, называется скалярная величина 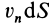 , где
, где 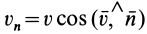 — проекция скорости на внешнюю нормаль к площадке.
— проекция скорости на внешнюю нормаль к площадке.
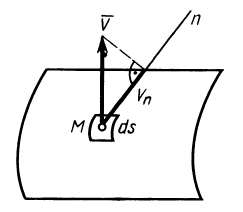
Рис. 112
Для замкнутой поверхности внешней нормалью в каждой ее точке называют нормаль, которая направлена во внешнюю часть объема, ограниченного поверхностью. Для незамкнутых поверхностей дополнительно уславливаются, какое направление нормали считать внешним.
Потоком 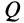 вектора скорости
вектора скорости 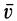 через поверхность
через поверхность 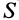 называют скалярную величину
называют скалярную величину

Для вычисления потока можно получить другие выражения, если учесть, что
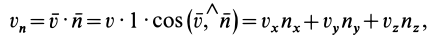
где 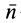 — единичный вектор, направленный по внешней нормали;
— единичный вектор, направленный по внешней нормали; 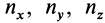 — его проекции на оси координат. Для них имеем:
— его проекции на оси координат. Для них имеем:
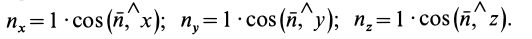
Кроме того,
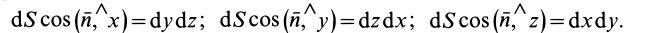
После этого для потока получаем
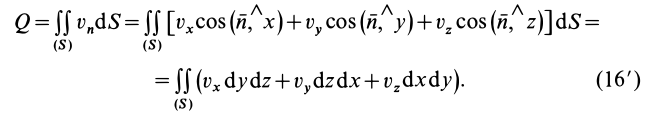
Наиболее часто используемое выражение для потока получают применением формулы Гаусса—Остроградского для преобразования интеграла по замкнутой поверхности 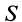 в интеграл по объему
в интеграл по объему 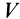 , ограниченному этой поверхностью:
, ограниченному этой поверхностью:
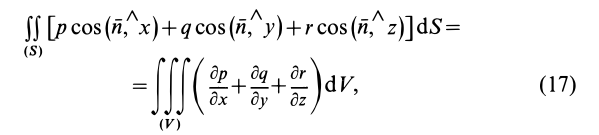
где 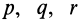 — любые функции переменных Эйлера, имеющие частные производные. Замкнутая поверхность должна быть при этом достаточно гладкой.
— любые функции переменных Эйлера, имеющие частные производные. Замкнутая поверхность должна быть при этом достаточно гладкой.
Если принять 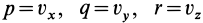 , то, применяя (17) для потока через замкнутую поверхность, имеем
, то, применяя (17) для потока через замкнутую поверхность, имеем
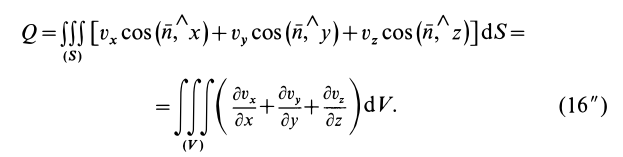
Ho
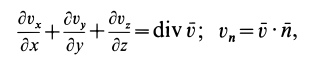
поэтому
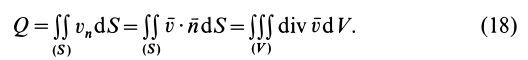
Для вектора вихря скорости поток через замкнутую поверхность равен нулю, так как с учетом формул для проекций вектора вихря на координатные оси имеем
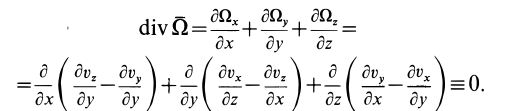
Из (18) для потока 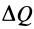 через элементарную замкнутую поверхность, ограничивающую объем
через элементарную замкнутую поверхность, ограничивающую объем 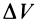 , приближенно имеем
, приближенно имеем
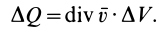
Отсюда получаем для дивергенции вектора скорости
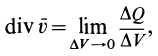
т. е. дивергенцию вектора скорости в какой-либо точке можно рассматривать как предел потока вектора скорости через замкнутую поверхность, приходящуюся на единицу объема, ограниченного поверхностью, при стягивании объема в эту точку.
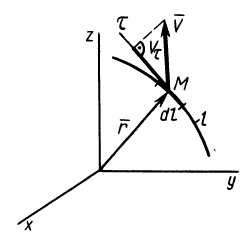
Рис. 113
Циркуляция вектора скорости: Для введения понятия циркуляции вектора скорости по какому-либо контуру следует выбрать контур 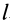 , разбить его на элементарные участки длиной
, разбить его на элементарные участки длиной 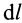 . Тогда циркуляцией вектора скорости
. Тогда циркуляцией вектора скорости 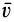 по элементарному контуру
по элементарному контуру 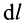 называют величину
называют величину 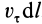 , где
, где 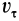 — проекция вектора скорости на положительное направление касательной к контуру в рассматриваемой точке (рис. 113). За положительное направление касательной к контуру, если контур замкнутый, выбирают то направление, при обходе контура в котором ограниченная им поверхность остается слева. Для незамкнутого контура о положительном направлении касательной уславливаются дополнительно.
— проекция вектора скорости на положительное направление касательной к контуру в рассматриваемой точке (рис. 113). За положительное направление касательной к контуру, если контур замкнутый, выбирают то направление, при обходе контура в котором ограниченная им поверхность остается слева. Для незамкнутого контура о положительном направлении касательной уславливаются дополнительно.
Циркуляция вектора скорости по всему контуру

Для вычисления циркуляции можно получить другие формулы, если учесть, что
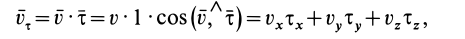
где 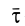 — единичный вектор в положительном направлении касательной к контуру;
— единичный вектор в положительном направлении касательной к контуру; 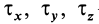 — его проекции на декартовы оси координат. Учитывая, что
— его проекции на декартовы оси координат. Учитывая, что
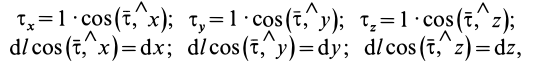
получим
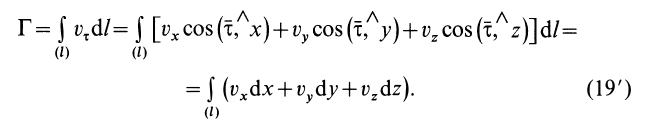
Ho
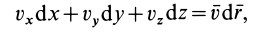
где 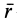 — радиус-вектор, проведенный из начала координат в точку
— радиус-вектор, проведенный из начала координат в точку 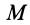 контура. Поэтому имеем
контура. Поэтому имеем
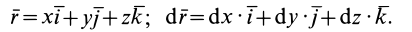
Таким образом,
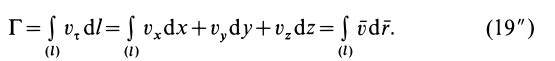
Для замкнутого контура можно применить формулу Стокса, преобразующую интеграл по контуру в интеграл по поверхности, натянутой на этот контур:
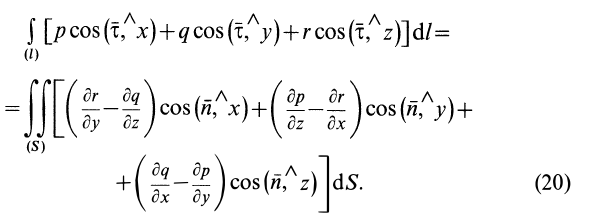
Если принять  , то, применяя (20) для замкнутого контура, имеем
, то, применяя (20) для замкнутого контура, имеем
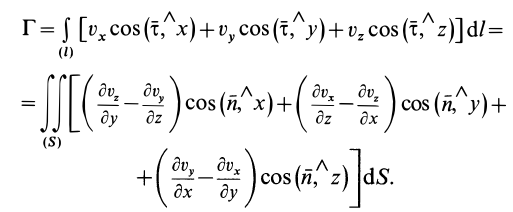
Учитывая, что
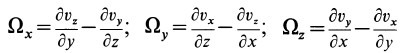
являются проекциями вихря скорости, для циркуляции по замкнутому контуру получим
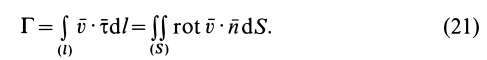
Если 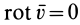 , т.е. движение сплошной среды является потенциальным, то циркуляция при таком движении по замкнутому контуру равна нулю, если контур не охватывает точек, в которых вихрь скорости отличен от нуля.
, т.е. движение сплошной среды является потенциальным, то циркуляция при таком движении по замкнутому контуру равна нулю, если контур не охватывает точек, в которых вихрь скорости отличен от нуля.
Для вектора силы 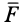 циркуляция по какому-либо контуру является работой силы на этом контуре.
циркуляция по какому-либо контуру является работой силы на этом контуре.
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |