
Исследование поведения функций с примерами решения
Содержание:
Критерий монотонности функции:
Прежде всего, сформулируем определение монотонной функции:
- Функция f называется неубывающей (невозрастающей) на интервале (а,b), если для любых двух точек
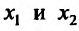
- Функция f называется возрастающей (убывающей) на интервале (а,b), если для любых двух точек
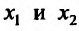 из интервала (а, b), удовлетворяющих условию
из интервала (а, b), удовлетворяющих условию 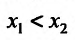 справедливо неравенство
справедливо неравенство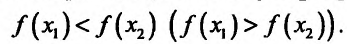 Неубывающие и невозрастающие функции называют монотонными функциями.
Неубывающие и невозрастающие функции называют монотонными функциями.
Монотонные функции
Возрастающие и убывающие функции называются строго монотонными функциями.
Например, функция у = х- возрастающая (строго монотонная) на всей числовой оси; функция 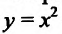 -возрастает на полуоси х > О и убывает при
-возрастает на полуоси х > О и убывает при 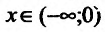 ; функция у = signx - неубывающая на всей числовой оси;
; функция у = signx - неубывающая на всей числовой оси; 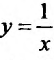 убывает при
убывает при 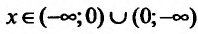 .
.
Теорема 14.1.1. (Критерий монотонности) Пусть функция 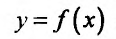 определена и дифференцируема на интервале (а,b). Для того, чтобы f не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы производная этой функции была неотрицательной (неположительной)
определена и дифференцируема на интервале (а,b). Для того, чтобы f не убывала (не возрастала) на этом интервале, необходимо и достаточно чтобы производная этой функции была неотрицательной (неположительной)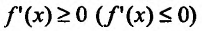 всюду на этом интервале. Для того чтобы функция / возрастала (убывала) на интервале (а, b), достаточно чтобы производная
всюду на этом интервале. Для того чтобы функция / возрастала (убывала) на интервале (а, b), достаточно чтобы производная 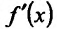 была положительной (отрицательной) на этом интервале.
была положительной (отрицательной) на этом интервале.
Доказательство: Пусть 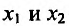 - любые две точки из интервала (а, b), удовлетворяющие условию
- любые две точки из интервала (а, b), удовлетворяющие условию 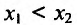 Поскольку функция f(x) дифференцируема, а стало быть и непрерывна на (а, b), то она непрерывна и дифференцируема на отрезке
Поскольку функция f(x) дифференцируема, а стало быть и непрерывна на (а, b), то она непрерывна и дифференцируема на отрезке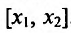 . Поэтому к функции
. Поэтому к функции 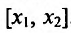 можно применить теорему Лагранжа:
можно применить теорему Лагранжа:
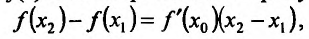 (14.1.1)
(14.1.1)
где 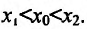 .
.
Необходимость. Пусть функция f дифференцируема на интервале (а, b) и не убывает (не возрастает) на этом интервале. Требуется доказать, что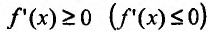 на этом интервале. Рассмотрим равенство (14.1.1). Левая часть равенства
на этом интервале. Рассмотрим равенство (14.1.1). Левая часть равенства 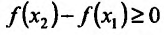
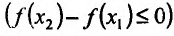 поскольку функция f не убывает (не возрастает) и
поскольку функция f не убывает (не возрастает) и 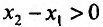 по условию, тогда и
по условию, тогда и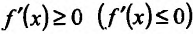 на интервале
на интервале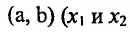 - любые две точки из интервала (а,b)).
- любые две точки из интервала (а,b)).
Достаточность. Пусть теперь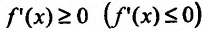 на интервале (а,b). Тогда из (14.1.1) следует, что
на интервале (а,b). Тогда из (14.1.1) следует, что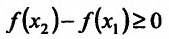
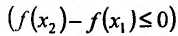 ,т.е.
,т.е.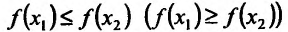 так
так 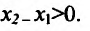
Поскольку 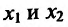 - любые две точки из интервала, то функция f не убывает (не возрастает ) на интервале (а, b).
- любые две точки из интервала, то функция f не убывает (не возрастает ) на интервале (а, b).
Аналогично теорема доказывается и для возрастающей (убывающей) функции.
Из доказанной теоремы следует, что для определения интервалов монотонности функции нужно:
- Найти область определения функции.
- Вычислить ее производную.
- Приравнять производную к нулю; полученные нули производной разобьют область определения на интервалы, в которых производная сохраняет знак.
- Определить знак производной в каждом интервале при помощи "пробной" точки и сделать вывод.
Пример:
Найти интервалы монотонности функции 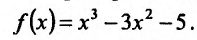
Решение:
Область определения заданной функции - вся числовая ось 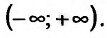 Производная
Производная 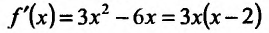 этой функции обращается в нуль в точках:
этой функции обращается в нуль в точках: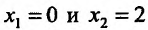 .
.
Составим схему изменения знаков производной:
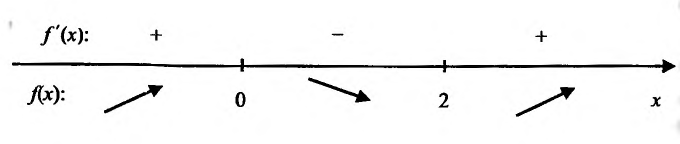
Согласно теореме' 14.1.1, данная функция возрастает при 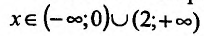 и убывает при
и убывает при 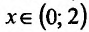 .
.
Функция 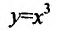 не убывает в области определения (при
не убывает в области определения (при 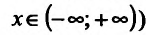 поскольку
поскольку 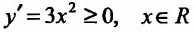 ;
;
Функция 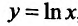 , определенная при
, определенная при 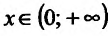 , возрастает, поскольку
, возрастает, поскольку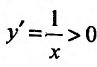
Экстремумы функций
Определение 14.2.1. Пусть функция f определена в некоторой окрестности точки 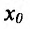 - Точка
- Точка 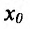 называется точкой максимума (минимума) функции f, если существует такая окрестность точки
называется точкой максимума (минимума) функции f, если существует такая окрестность точки 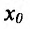 , что
, что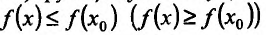 для всехx из этой окрестности.
для всехx из этой окрестности.
Если выполняются строгие неравенства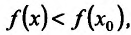
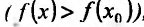 , то точка
, то точка 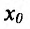 называется точкой строгого максимума (строгого минимума).
называется точкой строгого максимума (строгого минимума).
Точки максимума и минимума (строгого максимума и минимума) называются точками экстремума (строгого экстремума). 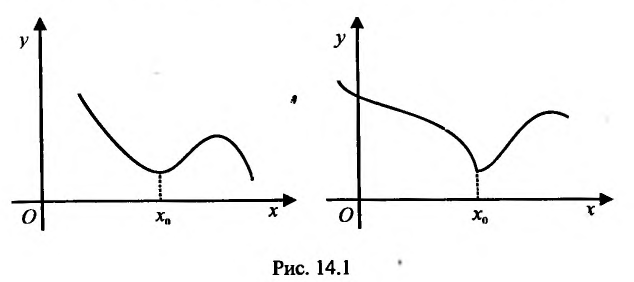
Теорема 14.2.1 .(необходимое условие экстремума) Если точка 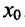 является точкой экстремума функции f определенной в некоторой окрестности точки
является точкой экстремума функции f определенной в некоторой окрестности точки 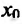 . то либо производная
. то либо производная 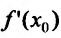 не существует, либо
не существует, либо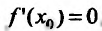
Справедливость этой теоремы следует из теоремы Ферма в силу определения точек экстремума. Действительно, если 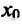 точка экстремума, то согласно определения экстремума это точка, в которой функция достигает наибольшего либо наименьшего значения, и в силу теоремы Ферма
точка экстремума, то согласно определения экстремума это точка, в которой функция достигает наибольшего либо наименьшего значения, и в силу теоремы Ферма 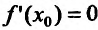 , если производная существует.
, если производная существует.
Функция может достигать экстремума также в точке, в которой производная не существует. Например, функция 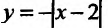 не имеет производной в точке х=2, но достигает в ней максимума: у= 0 при х=2, а для всякой другой точки y
не имеет производной в точке х=2, но достигает в ней максимума: у= 0 при х=2, а для всякой другой точки y 0 (рис. 14.3). Функция
0 (рис. 14.3). Функция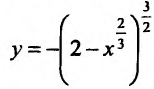 не имеет конечной производной в точке х=0, поскольку
не имеет конечной производной в точке х=0, поскольку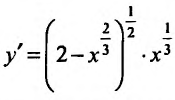 при х=0 обращается в бесконечность, но в этой точке функция имеет Минимум:
при х=0 обращается в бесконечность, но в этой точке функция имеет Минимум: 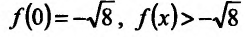 при
при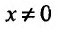 (рис. 14.4).
(рис. 14.4).
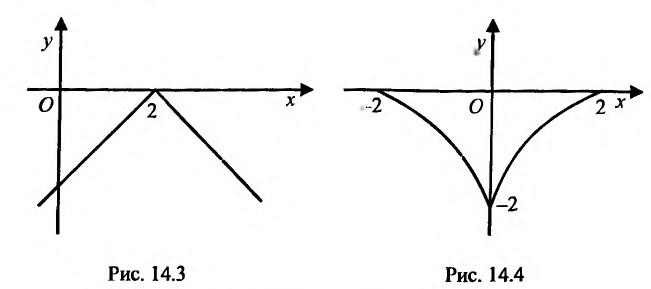
Из приведенных рассуждений следует, что точки экстремума функции нужно искать среди тех точек её области определения, где производная функции равна нулю или не существует.
Если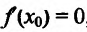 , это еще не значит, что в точке
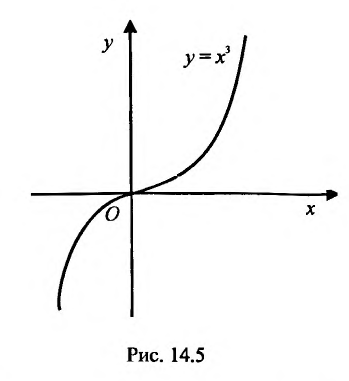
, это еще не значит, что в точке 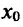 есть экстремум. Примером может служить функция
есть экстремум. Примером может служить функция 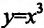 . В точке х=0 её производная
. В точке х=0 её производная 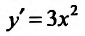 равна нулю, но экстремума в этой точке функция не имеет. График функции изображен на рисунке 14.5.
равна нулю, но экстремума в этой точке функция не имеет. График функции изображен на рисунке 14.5.
Точки области определения функции, в которых производная равна нулю, называются стационарными, а в которых производная не существует, называются критическими.
Каждая стационарная (критическая) точка - это точка возможного экстремума. Однако сделать заключение о том, что в данной стационарной (критической) точке на самом деле экстремум, можно лишь на основании дополнительного исследования, т.е. на основании достаточных условий экстремума.
Теорема 14.2.2. (первое достаточное условие экстремума) Пусть функция f определена, дифференцируема в некоторой окрестности точки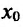 и непрерывна слева и справа от точки
и непрерывна слева и справа от точки 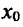 - Тогда если в пределах указанной окрестности производная
- Тогда если в пределах указанной окрестности производная 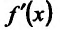 положительна (отрицательна) слева от точки
положительна (отрицательна) слева от точки 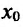 и отрицательна (положительна) справа от точки
и отрицательна (положительна) справа от точки 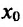 , то функция f имеет в точке
, то функция f имеет в точке 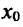 локальный максимум (минимум):
локальный максимум (минимум):
- если
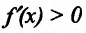 на
на 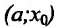 и
и 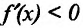 на
на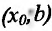 , то точка
, то точка 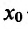 - точка максимума функции f(x);
- точка максимума функции f(x); - если
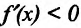 на
на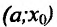 и
и 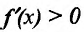 на
на 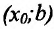 , то точка
, то точка 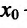 - точка минимума функции f(x);
- точка минимума функции f(x);
Если же в пределах указанной окрестности точки 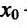 производная
производная 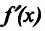 имеет один и тот же знак слева и справа от точки
имеет один и тот же знак слева и справа от точки 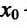 , то экстремума в точке
, то экстремума в точке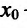 нет.
нет.
Доказательство. Докажем первое утверждение теоремы.
Предположим, что 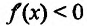 на интервале
на интервале 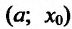 . Поскольку функция
. Поскольку функция 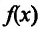 непрерывна в точке
непрерывна в точке 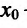 , то, в силу теоремы 14.1.1, она убывает на полуинтервале
, то, в силу теоремы 14.1.1, она убывает на полуинтервале 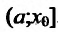 - Следовательно, для любого х
- Следовательно, для любого х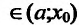 выполняется неравенство
выполняется неравенство 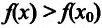 .
.
Пусть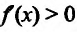 на интервале
на интервале 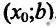 . Так как функция
. Так как функция 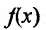 непрерывна в точке
непрерывна в точке 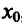 , то она возрастает на полуинтервале
, то она возрастает на полуинтервале 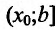 Тогда для любого
Тогда для любого 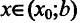 выполняется неравенство
выполняется неравенство 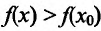 .
.
В результате получается, что при любом 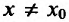 из интервала (а;b) выполняется неравенство
из интервала (а;b) выполняется неравенство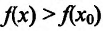 . Это значит, что точка
. Это значит, что точка 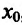 -точка минимума функции
-точка минимума функции 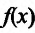 .
.
Второе утверждение теоремы доказывается аналогично. 
Пример:
Найти точки экстремума функции'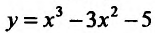 .
.
Решение:
Поскольку 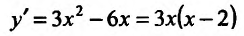 (см. пример 14.1.1) и при переходе через точку х=0 производная меняет знак с плюса на минус, а при переходе через точку х=2- с минуса на' плюс, то точка х=0 - точка максимума, а х=2 - точка минимума.
(см. пример 14.1.1) и при переходе через точку х=0 производная меняет знак с плюса на минус, а при переходе через точку х=2- с минуса на' плюс, то точка х=0 - точка максимума, а х=2 - точка минимума.
Производная функции 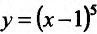 , определенной для
, определенной для 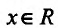 , обращается в нуль в одной точке х=1:
, обращается в нуль в одной точке х=1: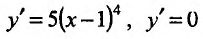 при х=1. Поскольку
при х=1. Поскольку 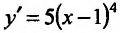 положительна как слева, так и справа от этой точки, то функция
положительна как слева, так и справа от этой точки, то функция 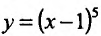 не имеет точек экстремума.
не имеет точек экстремума.
Теорема 14.2.3. (второе достаточное условие экстремума) Если функция f определена в некоторой окрестности точки 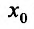 и в точке
и в точке 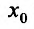 она имеет конечную вторую производную, причем
она имеет конечную вторую производную, причем  то при
то при 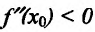 -точка
-точка 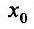 является точкой максимума, а при
является точкой максимума, а при 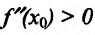 - точка
- точка 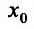 является точкой минимума.
является точкой минимума.
Доказательство: Поскольку функция f дважды дифференцируема в точке 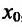 , то для нее справедлива формула Тейлора с остаточным членом в форме Лагранжа и функцию f можно представить
, то для нее справедлива формула Тейлора с остаточным членом в форме Лагранжа и функцию f можно представить
в виде:
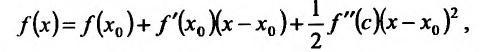
где точка с расположена между 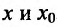 . По условию теоремы
. По условию теоремы 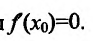 . Тогда формула Тейлора принимает вид:
. Тогда формула Тейлора принимает вид:
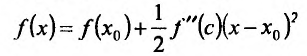
или
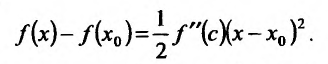
Поскольку 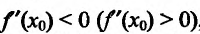 , то существует окрестность точки
, то существует окрестность точки 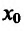 в которой
в которой 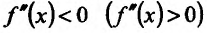 и, следовательно,
и, следовательно,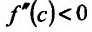
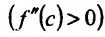 , так как точка с расположена в окрестности точки
, так как точка с расположена в окрестности точки 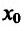 . Если
. Если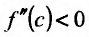 , то слагаемое
, то слагаемое 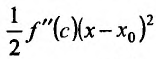 так же меньше нуля. Значит разность
так же меньше нуля. Значит разность 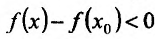 , т.е.
, т.е.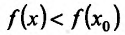 и точка
и точка 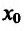 - точка максимума. Если же
- точка максимума. Если же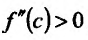 , то
, то 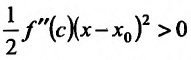 и. следовательно, разность
и. следовательно, разность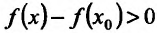 , т.е.
, т.е. 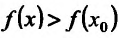 и точка
и точка 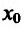 - точка минимума.
- точка минимума.
Пример:
Найти точки экстремума функции 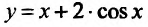 на отрезке
на отрезке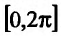 .
.
Решение:
Вычислим первую и вторую производные заданной функции: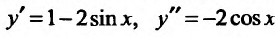 . Из уравнения l-2sinx = 0 определяем стационарные точки на отрезке
. Из уравнения l-2sinx = 0 определяем стационарные точки на отрезке 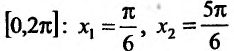 •
•
Теперь находим знак второй производной в каждой стационарной точке и определяем ее характер, используя теорему 14.2.3. Поскольку
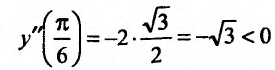 , то
, то 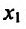 - точка максимума,
- точка максимума,
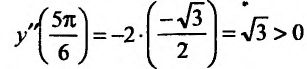 то точка
то точка 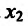 - точка минимума.
- точка минимума.
Теорема 14.2.4. (третье достаточное условие экстремума). Пусть функция f определена в некоторой окрестности точки 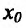 и в точке
и в точке 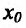 функция f имеет производные до порядка n включительно, причем
функция f имеет производные до порядка n включительно, причем 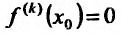 для
для 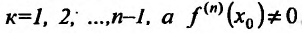 Тогда, если n- четное и
Тогда, если n- четное и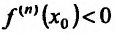 , то
, то 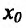 - точка максимума, а если
- точка максимума, а если 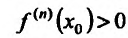 , то
, то 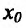 - точка минимума. Если же n - нечетное, то функция f в точке
- точка минимума. Если же n - нечетное, то функция f в точке 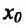 экстремума не имеет.
экстремума не имеет.
Пример:
Исследовать на экстремум функцию 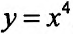 .
.
Решение:
Функция определена, непрерывна и дифференцируема на всей числовой оси. Найдем первую производную- 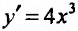 и, приравняв ее к нулю, определяем стационарную точку х=0. Вычисляем последовательно производные
и, приравняв ее к нулю, определяем стационарную точку х=0. Вычисляем последовательно производные 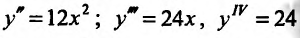 . Применив теорему 14.2.4. определяем, что х=0 - точка минимума.
. Применив теорему 14.2.4. определяем, что х=0 - точка минимума.
Сформулированные теоремы позволяют решать определенный круг задач. Например, требуется определить наибольшее (найме шее) значение функции f на отрезке [а, b]. Для этого следует на ней все точки, в которых производная функции либо равна нулю, ли' не существует. Затем из этих точек выбираем те, которые принадлежат отрезку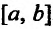 . После этого достаточно лишь сравнить между собой по величине значения функции в отобранных точках и значения функции на концах отрезка
. После этого достаточно лишь сравнить между собой по величине значения функции в отобранных точках и значения функции на концах отрезка 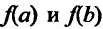 . Наибольшее (найме шее) из этих значений и будет наибольшим (наименьшим) значениях функции на отрезке
. Наибольшее (найме шее) из этих значений и будет наибольшим (наименьшим) значениях функции на отрезке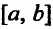 .
.
Пример:
Найти наибольшее и наименьшее значениях функции 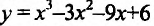 на отрезке [—2;2].
на отрезке [—2;2].
Решение:
Вычислив производную и приравняв ее к ну: 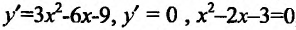 , находим стационарные точки данного функции:
, находим стационарные точки данного функции: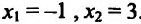
Отрезку [-2;2] принадлежит только одна точка 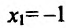 . Вычисляем значения функции в точке
. Вычисляем значения функции в точке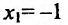 и на концах отрезка:
и на концах отрезка: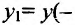
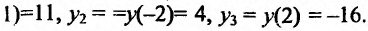 . Сравнивая полученные значения, определяем, что
. Сравнивая полученные значения, определяем, что 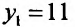 наибольшее значение функции, а
наибольшее значение функции, а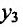
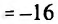 наименьшее значение функции на отрезке [-2;2].
наименьшее значение функции на отрезке [-2;2].
Выпуклость и точки перегиба
Пусть функция f определена на интервале (а; b) и пусть точки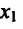 и
и 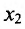 такие, что выполняется неравенство
такие, что выполняется неравенство 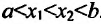 . Проведем прямую через точки графика функции у = f(x). Ее уравнение имеет вид:
. Проведем прямую через точки графика функции у = f(x). Ее уравнение имеет вид: 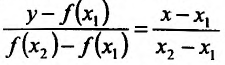
Разрешим это уравнение относительно у:
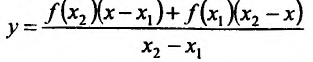
ИЛИ
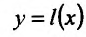 , где
, где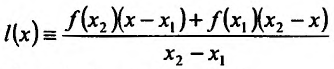
Ясно, что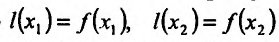 .
.
Определение 14.3.1. Функция f называется выпуклой вверх (выпуклой вниз) на интервале 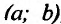 , если для любых точек
, если для любых точек 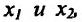
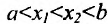 и для любой точки
и для любой точки 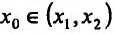 выполняется неравенство
выполняется неравенство

соответственно. А сам интервал называется интервалом выпуклости вверх (выпуклости вниз).
Геометрически это означает, что любая точка хорды АВ (т.е. отрезка прямой у=1(х) с концами в точках А и В) лежит не выше (не ниже) точки графика функции , соответствующей тому же значению аргумента.
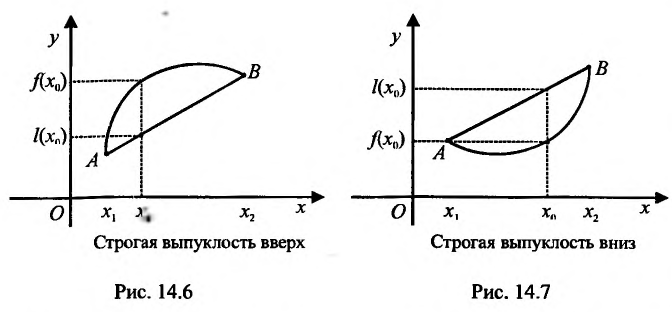
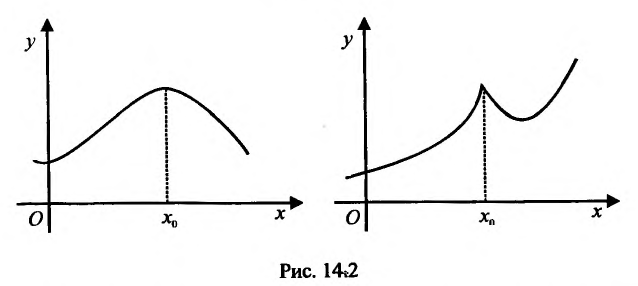
Если неравенства (14.3.1) и (14.3.2) строгие, то функция f называется строго выпуклой вверх (рис. 14.6) (строго выпуклой вниз (рис. 14.7)). В этом случае любая точка хорды АВ, исключая ее концы, лежит ниже (выше) соответствующей точки графика функции
Теорема 14.3.1. (достаточное условие строгой выпуклости) Если функция f определена и дважды дифференцируема на интервале (а,b), то 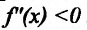 на (а, b) функция f строго выпукла вверх, а при
на (а, b) функция f строго выпукла вверх, а при 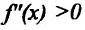 на (а,b) функция f строго выпукла вниз на этом интервале.
на (а,b) функция f строго выпукла вниз на этом интервале.
Доказательство. Пусть функция f определена и дважды непрерывно дифференцируема на интервале (а, b). Возьмем некоторые точки  на интервале (а, b), такие, что
на интервале (а, b), такие, что 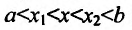 и проведем хорду АВ: у=l(х). Рассмотрим разность:
и проведем хорду АВ: у=l(х). Рассмотрим разность:
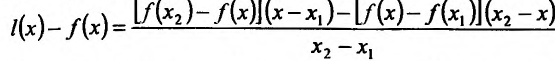
Применяя теорему Лагранжа к каждой разности, т.е. к 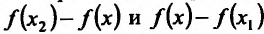 . получим
. получим
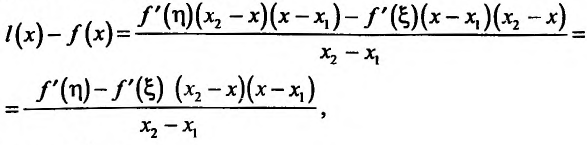
где 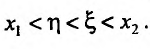
Снова применим теорему Лагранжа к разности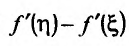 Будем иметь.
Будем иметь.
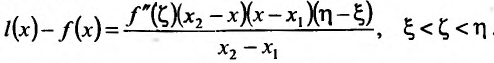
Отсюда видно, что если 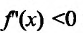 на (а, b) , то и и поэтому-
на (а, b) , то и и поэтому- 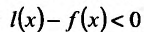 , т.к.
, т.к. 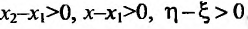 Следовательно. l(х)
Следовательно. l(х)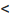 f(x),- функция f строго выпукла вверх; если же
f(x),- функция f строго выпукла вверх; если же на (a, b) , го l(x)> f(x),- функция f строго выпукла вниз. Теорема дока-jaiia.
на (a, b) , го l(x)> f(x),- функция f строго выпукла вниз. Теорема дока-jaiia. 
Заметим, что условие знакопостоянства второй производной не является необходимым условием. Так, функция 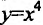 строго выпукла вниз на всей числовой оси, однако ее вторая производная
строго выпукла вниз на всей числовой оси, однако ее вторая производная 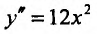 обращается в 0 при x=0. Следовательно, может быть, что для строго выпуклой функции вторая производная и не сохраняет знак. Но если для функции вторая производная сохраняет знак на некотором интервале, то график функции строго выпуклый (при
обращается в 0 при x=0. Следовательно, может быть, что для строго выпуклой функции вторая производная и не сохраняет знак. Но если для функции вторая производная сохраняет знак на некотором интервале, то график функции строго выпуклый (при 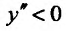 вверх и при
вверх и при 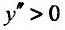 вниз).
вниз).
Определение 14.3.2. Пусть фунщия f определена в некоторой окрестности точки 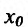 'и непрерывна в этой точке. Точка
'и непрерывна в этой точке. Точка 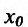 называется точкой перегиба функции f, если она является одновременно концом интервала строгой выпуклости вверх и строгой выпуклости вниз, т.е. она отделяет выпуклые части вверх от выпуклых частей внешнего графика функции.
называется точкой перегиба функции f, если она является одновременно концом интервала строгой выпуклости вверх и строгой выпуклости вниз, т.е. она отделяет выпуклые части вверх от выпуклых частей внешнего графика функции.
Теорема 14.3.2. (необходимое условие точки перегиба) Если функция f определена и дважды непрерывно дифференцируема на (а,b) и 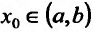 - точка перегиба, то
- точка перегиба, то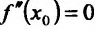
Доказательство. Пусть задана функция f, которая определена и дважды' непрерывно дифференцируема на (а.b) и пусть точка 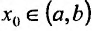 является точкой перегиба. Предположим, что вторая производная
является точкой перегиба. Предположим, что вторая производная 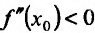 (либо
(либо 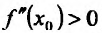 ). Тогда в силу непрерывности второй производной найдется окрестность точки
). Тогда в силу непрерывности второй производной найдется окрестность точки 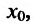 в которой
в которой 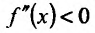 (либо
(либо 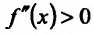 ) и, следовательно, функция f в этой окрестности точки
) и, следовательно, функция f в этой окрестности точки 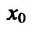 строго выпукла вверх (вниз), что противоречит тому, что
строго выпукла вверх (вниз), что противоречит тому, что 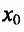 - точка перегиба. Полученное противоречие и доказывает теорему.
- точка перегиба. Полученное противоречие и доказывает теорему. 
Из теоремы вытекает, что точками перегиба дважды дифференцируемой функции могут быть лишь точки, в которых вторая производная обращается в нуль либо не существует.
Сформулируем и докажем теперь достаточные условия точки перегиба.
Теорема 14.3.3. Если функция f определена и дважды дифференцируема на интервале (а,b), кроме, быть может точки 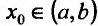 , в которой она, однако, непрерывна, и ее вторая производная меняет знак при переходе аргумента через точку
, в которой она, однако, непрерывна, и ее вторая производная меняет знак при переходе аргумента через точку 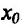 , то точка
, то точка 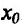 является точкой перегиба функции f
является точкой перегиба функции f
Действительно, в силу теоремы 14.3.1 точка 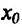 является одновременно концом интервала строгой выпуклости вверх и концом интервала строгой выпуклости вниз - т.е.
является одновременно концом интервала строгой выпуклости вверх и концом интервала строгой выпуклости вниз - т.е. 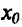 - точка перегиба.
- точка перегиба.
Теорема 14.3.4. Если f трижды непрерывно дифференцируема на (а,b) и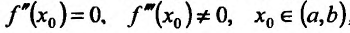 , то
, то 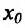 - точка перегиба.
- точка перегиба.
Доказательство (проведем для случая f"(x0) > 0). Так как по предположению 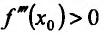 , то существует окрестность точки
, то существует окрестность точки 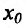 , в которой
, в которой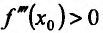 и, следовательно, функция
и, следовательно, функция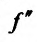 возрастает, обращаясь в нуль при x=
возрастает, обращаясь в нуль при x=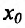 , т.е. функция
, т.е. функция 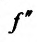 меняет знак при переходе через точку х=
меняет знак при переходе через точку х=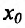 . Следовательно, в силу теоремы 14.3.3, точка
. Следовательно, в силу теоремы 14.3.3, точка 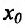 -точка перегиба.
-точка перегиба. 
Теорема 14.3.5. Пусть функция f непрерывно дифференцируема n раз на (а,b), причем
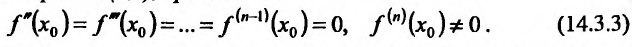 Тогда если п нечетно, то n - точка перегиба, если же n четно, то
Тогда если п нечетно, то n - точка перегиба, если же n четно, то 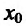 не является точкой перегиба.
не является точкой перегиба.
Итак, из изложенного материала вытекает, что выпуклость вверх или вниз графика функции f зависит от знака ее второй производной. Оказывается, что и расположение графика функции относительно касательной также связано со знаком второй производной, т.е. если функция f имеет вторую производную, все значения которой имеют один и тот же знак, то все точки графика функции f лежат над (под) касательной.
Рассмотрим пример, иллюстрирующий исследование графика функции на выпуклость и точки перегиба.
Пример 14.3.1. Найти интервалы выпуклости и точки перегиба графика функции 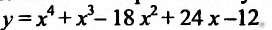
Решение. Функция определена для всех 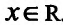 . Вычисляем последовательно первую и вторую производные функции:
. Вычисляем последовательно первую и вторую производные функции:
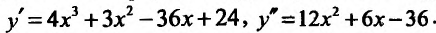
Приравняв вторую производную к нулю 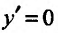 , т.е.
, т.е. 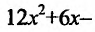
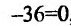 , находим
, находим 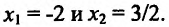
Составляет схему изменения знаков второй производной:

Следовательно, у">0 на интервалах 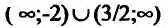 и функция выпукла вниз;
и функция выпукла вниз; 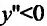 на интервале (-2;3/2) и функция выпукла вверх на этом интервале. Так как при переходе через точки
на интервале (-2;3/2) и функция выпукла вверх на этом интервале. Так как при переходе через точки 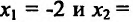 3/2 вторая производная меняет знак, то точки (-2;-124) и (3/2;-129/16) являются точками перегиба графика функции.
3/2 вторая производная меняет знак, то точки (-2;-124) и (3/2;-129/16) являются точками перегиба графика функции.
Рассмотрим пример из микроэкономики:
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
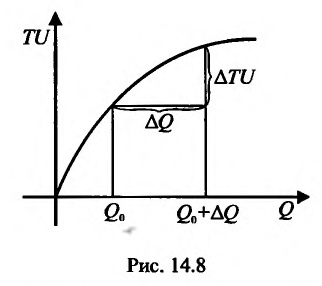
Это означает существование функции полезности TU аргумента Q -количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Построим прямоугольную систему координат и отложим по горизонтальной оси Ох количество потребляемого товара Q, а по вертикальной оси Оу - общую полезность TU (см. рис. 14.3). Рассмотрим график функции TU = TU(Q). Точка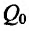 на горизонтальной оси означает количество приобретенного товара, величина
на горизонтальной оси означает количество приобретенного товара, величина 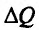 -добавочный приобретенный товар. Разность
-добавочный приобретенный товар. Разность 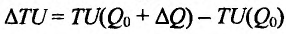 - добавочная полезность, полученная от покупки добавочного товара
- добавочная полезность, полученная от покупки добавочного товара 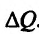 . Добавочная полезность от последней приобретенной порции товара (или единицы товара) вычисляется по формуле
. Добавочная полезность от последней приобретенной порции товара (или единицы товара) вычисляется по формуле 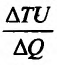 (см. Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 122). Переходя к пределу при
(см. Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 122). Переходя к пределу при 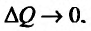 . получим формулу для определения предельной полезности MU:
. получим формулу для определения предельной полезности MU:
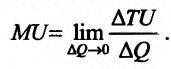
Но предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю, равен производной функции.
Следовательно, предельная полезность равна производной функции полезности TU=TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции 
Асимптоты графика функции
Рассмотрим функцию f определенную на интервале (а;b), . Если 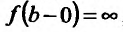 , то прямую х=n называют левосторонней вертикальной асимптотой графика функции f если
, то прямую х=n называют левосторонней вертикальной асимптотой графика функции f если 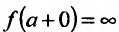 , то прямую х=а называют правосторонней вертикальной асимптотой графика функции f и если , то прямую х=с в плоскости хОу называют двусторонней вертикальной асимптотой графика функции f.
, то прямую х=а называют правосторонней вертикальной асимптотой графика функции f и если , то прямую х=с в плоскости хОу называют двусторонней вертикальной асимптотой графика функции f.
Заметим, что вертикальными асимптотами являются, как правило, нули знаменателей дробно-рациональных функций.
Если функция f определена на и для постоянных 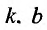 выполняется соотношение
выполняется соотношение

то прямая у = kх + b- называется наклонной асимптотой вправо графика функции f Если соотношение (14.4.1) выполняется и при , то прямая 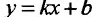 - называется наклонной асимптотой влево. Из (14.4.1) следует, что если
- называется наклонной асимптотой влево. Из (14.4.1) следует, что если 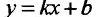 - наклонная вправо (влево) асимптота, то постоянные k и b определяются по формулам (из предельных соотношений):
- наклонная вправо (влево) асимптота, то постоянные k и b определяются по формулам (из предельных соотношений):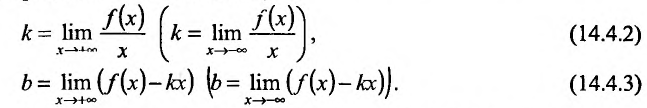
И наоборот, если пределы (14.4.2) и (14.4.3) существуют и конечны, то прямая у = kх + b- наклонная вправо (влево) асимптота графика функции f
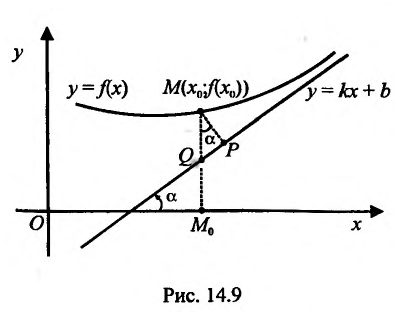
Рассмотрим геометрический смысл асимптоты. Пусть 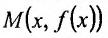 точка графика функцииf, точка
точка графика функцииf, точка 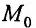 - ее проекция на ось Ох.
- ее проекция на ось Ох.
На рис. 14.9 видно, что отрезок 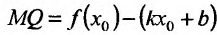 , а MP = MQ cos a.. По определению, прямая y = kx + b называется асимптотой, если
, а MP = MQ cos a.. По определению, прямая y = kx + b называется асимптотой, если 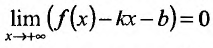 . Это значит, что и
. Это значит, что и 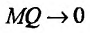 при
при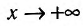 . Расстояние от точки М до прямой, как легко видно, равно MP = MQ cos а. Поэтому, если
. Расстояние от точки М до прямой, как легко видно, равно MP = MQ cos а. Поэтому, если 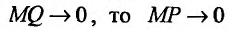 при
при 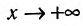 . Следовательно, асимптота может быть определена как прямая, расстояние до которой от графика функции, т.е. отрезок MP, стремится к нулю, когда точка М стремится к бесконечности по графику функцииf Таким образом, функция f при
. Следовательно, асимптота может быть определена как прямая, расстояние до которой от графика функции, т.е. отрезок MP, стремится к нулю, когда точка М стремится к бесконечности по графику функцииf Таким образом, функция f при 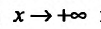 ведет себя почти как линейная функция, если ее график имеет асимптоту у = kх + b.
ведет себя почти как линейная функция, если ее график имеет асимптоту у = kх + b.
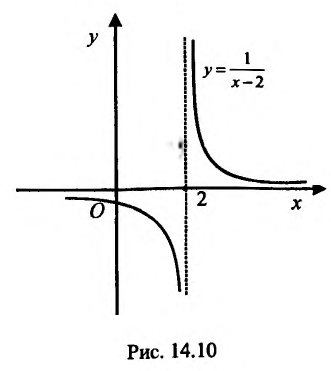
Пример:
График функции 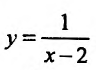 имеет вертикальную асимптоту х = 2, так как
имеет вертикальную асимптоту х = 2, так как 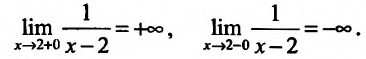
Пример:
Найти асимптоты графика функции 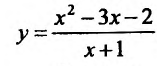
Решение:
Область определения функции D(f):  . Вычислим пределы:
. Вычислим пределы:
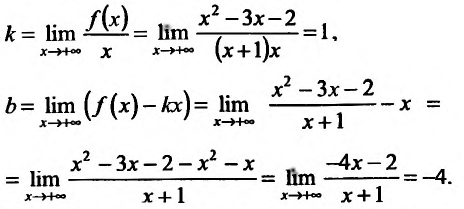
Так как значения пределов останутся такими же и при  , то прямая у = х-4 является наклонной вправо и влево асимптотой графика функции. Кроме того, х = — 1 является двусторонней вертикальной асимптотой, так как
, то прямая у = х-4 является наклонной вправо и влево асимптотой графика функции. Кроме того, х = — 1 является двусторонней вертикальной асимптотой, так как 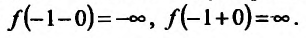
Общая схема исследования функций и построение их графиков
Под исследованием функций понимается изучение ее изменения в зависимости от изменения аргумента. Исследование функций и построение их графиков можно проводить по следующей схеме:
- Найти область определения и множество значений функции; исследовать на непрерывность, найти точки разрыва и выяснить характер точек разрыва; определить вертикальные асимптоты. Найти точки пересечения с осями координат.
- Исследовать функцию на периодичность; четность, нечетность.
- Исследовать поведение функции на границе области определения; найти асимптоты графика функции.
- Исследовать функцию на монотонность, выяснить характер экстремумов.
- Определить интервалы выпуклости графика функции, точки перегиба.
- Составить таблицу значений функции куда включаются все точки графика функции, найденные на предыдущих этапах исследования и необходимые дополнительные контрольные точки.
- Используя все полученные результаты построить график функции.
Пример:
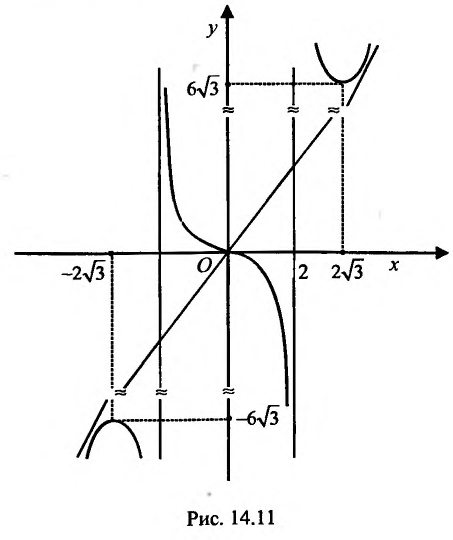
Построить график функции 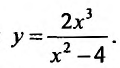
Решение:
Проведем полное исследование функции по указанной схеме.
1. Функция определена и непрерывна при всех 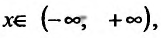 кроме точек х = ±2. Множество значений функции
кроме точек х = ±2. Множество значений функции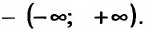
Прямые- х = ±2 являются вертикальными асимптотами, т.к.
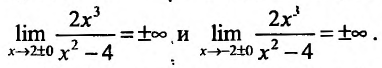
График пересекает оси координат в точке O(0; 0).
2. Функция не периодическая. Функция не четная, т.к. выпол-
няется равенство: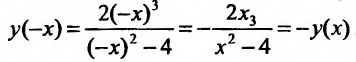 . График
. График
функции симметричный относительно начала координат. Поэтому достаточно провести исследование функции на полуинтервале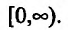
3. Найдем наклонную асимптоту. Для этого вычислим пределы:
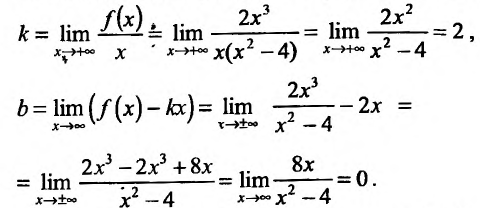
Подставив значения k и b уравнение 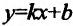 , получим уравнение асимптоты у =2х.
, получим уравнение асимптоты у =2х.
4. Для нахождения промежутков возрастания и убывания найдем первую производную:
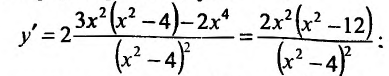
приравняем ее к нулю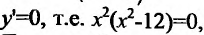 , и найдем стационарные точки
, и найдем стационарные точки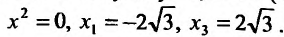 . Составляем схему изменения знаков первой производной:
. Составляем схему изменения знаков первой производной:
 На промежутке
На промежутке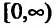 производная
производная 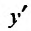 обращается в нуль в точках
обращается в нуль в точках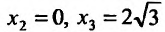 и обращается в бесконечность в точке х = 2. Поскольку при
и обращается в бесконечность в точке х = 2. Поскольку при 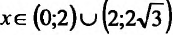 производная
производная 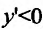 , то функция на этих интервалах убывает, а на интервале
, то функция на этих интервалах убывает, а на интервале 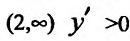 , следовательно, функция возрастает. Очевидно, что точка
, следовательно, функция возрастает. Очевидно, что точка 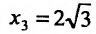 является точкой минимума.
является точкой минимума.
5. Для нахождения промежутков выпуклости и точек перегиба, найдем вторую производную 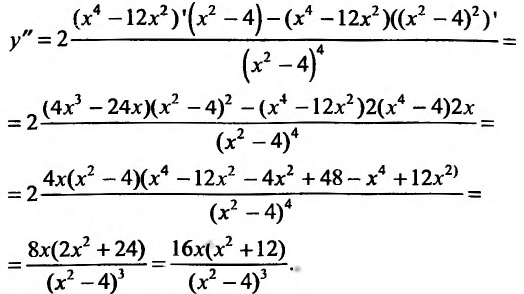
Вторая производная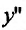 обращается в нуль в точке х = 0 и в бесконечность в точке х = 2. Составляем схему изменения знаков второй производной:
обращается в нуль в точке х = 0 и в бесконечность в точке х = 2. Составляем схему изменения знаков второй производной:
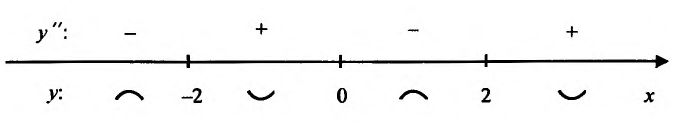
На интервале 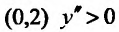 и поэтому функция выпукла вверх, а на интервале
и поэтому функция выпукла вверх, а на интервале 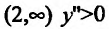 и, следовательно, функция выпукла вниз. Кроме того, точка х = 0 является точкой перегиба, т.к. вторая производная меняет знак при переходе через эту точку.
и, следовательно, функция выпукла вниз. Кроме того, точка х = 0 является точкой перегиба, т.к. вторая производная меняет знак при переходе через эту точку.
6. Используя результаты исследования и учитывая нечетность функции, строим график (рис. 14.11).
Пример:
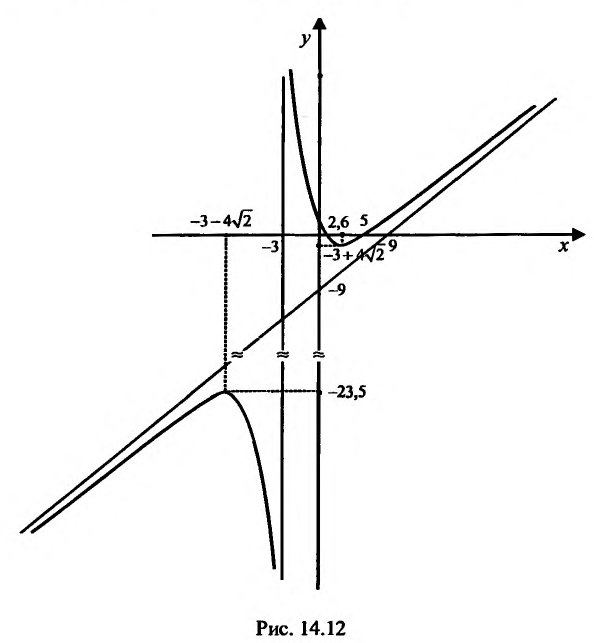
Провести полное исследование целевой функции потребления 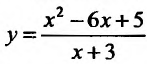 от услуги х и построить её график.
от услуги х и построить её график.
Решение:
Проведём полное и разностороннее изучение свойств функции, применив изложенную выше схему.
1) Функция определена и непрерывна для всех 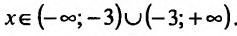 Точка х= -3 является точкой разрыва. Так
Точка х= -3 является точкой разрыва. Так
как 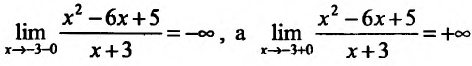 то прямая х =
то прямая х =
-3 является вертикальной асимптотой. Если х=0, то 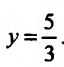 Если
Если
у=О, тс получим уравнение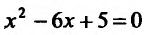 , решив которое найдём
, решив которое найдём
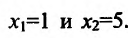 . Итак, график функции
. Итак, график функции 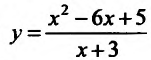 пересекает оси
пересекает оси
координат в точках: 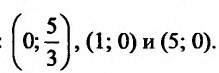
2) Функция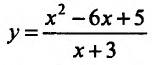 не является периодической
не является периодической
3) Исследуемая функция не является ни чётной, ни нечётной, гак как
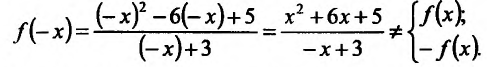
4) Исследуем существование наклонных асимптот. Для этого вычислим пределы;
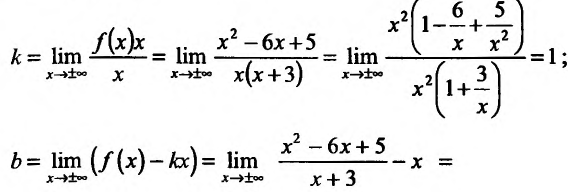
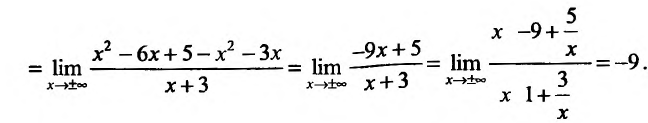
Итак, при  график функции
график функции 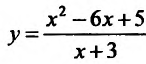 , имеет наклонную асимптоту у=х-9.
, имеет наклонную асимптоту у=х-9.
Исследуем повеление функции на границе области определения. Поведение функции в окрестности точки х = -3 исследовано. Поэтому изучим поведение функции при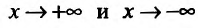 , вычислив пределы:
, вычислив пределы:
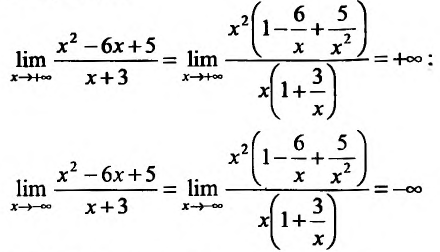
5) Первая производная
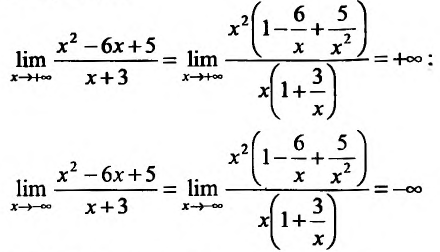
обращается в нуль в точках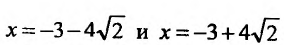 и стремится к бесконечности при
и стремится к бесконечности при 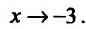 . Для определения интервалов монотонности функции и точек экстремума, построим схему изменения знаков производной:
. Для определения интервалов монотонности функции и точек экстремума, построим схему изменения знаков производной:

Поскольку 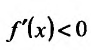 при
при 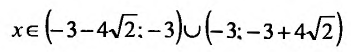 и
и 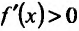 при
при
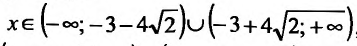 то функция убывает при
то функция убывает при
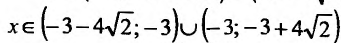 и возрастает при
и возрастает при
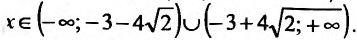 Следовательно, точка
Следовательно, точка
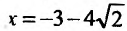 - точка максимума, а точка
- точка максимума, а точка 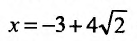 - точка минимума. Значения функции в этих точках равны:
- точка минимума. Значения функции в этих точках равны:
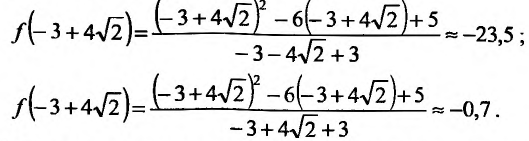
6) Вторая производная не обращается в нуль и стремится к бесконечности при 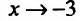 . Построим схему изменения знаков второй производной:
. Построим схему изменения знаков второй производной:
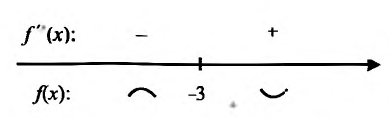
Поскольку 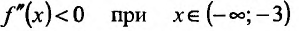 и
и 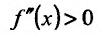 при
при 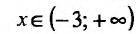 , то график функции является выпуклым вверх на интервале
, то график функции является выпуклым вверх на интервале 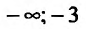 и выпуклым вниз при
и выпуклым вниз при 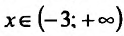 . Точка х = -3 не является точкой перегиба, так как это точка разрыва функции.
. Точка х = -3 не является точкой перегиба, так как это точка разрыва функции.
По результатам исследования строим график функции. Вначале строим систему координат; затем вертикальную и горизонтальную асимптоты; наносим точки пересечения с осями координат и точки экстремума функции. Затем строим график (рис. 14.12).
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной