Иррациональные уравнения с примерами решения
Уравнения, в которых неизвестное участвует под знаком корня называется иррациональным.
Содержание:
Рассмотрим методы решения некоторых видов иррациональных уравнений.
Рассмотрим простое иррациональное уравнение вида:
Пусть выражения f(х), g(x) принимают неотрицательные значения. Возводя обе части уравнения в квадрат, получим равносильное уравнение.
Так как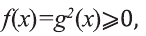 
Значит, решение уравнения (1) осуществляется по правилу:
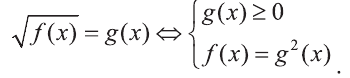
Аналогично уравнение вида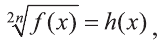 
равносильно системе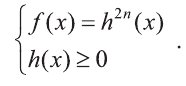 
Пример:
Решите уравнение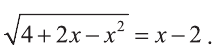 
Решение:
Возводя обе части уравнения в квадрат, получим равносильное уравнение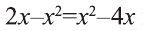 
или 
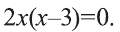. Отсюда получим корни 
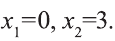Так как х>2, то х=3 - решение данного уравнение.
Уравнения вида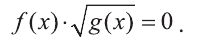 
Для того чтобы произведение двух выражений обращалось в нуль, необходимо и достаточно равенство нулю, хотя бы одного из сомножителей.
Значит, для того чтобы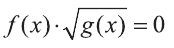 
должно выполняться равенство или 
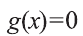совокупность равенств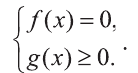 
Этот факт мы кратко будем записывать так: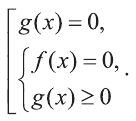 
Пример:
Решите уравнение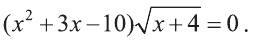 
Решение:
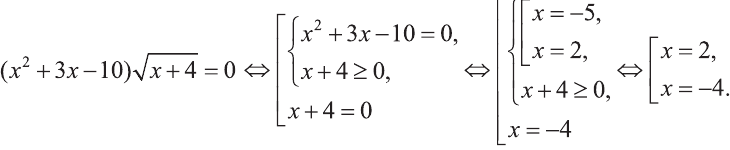
Ответ: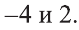 
Пример:
Решите уравнение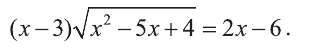 
Решение:
Данное уравнение приводится к виду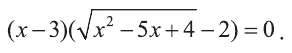 
Так как система 
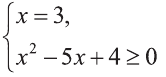не имеет решении, то достаточно рассмотреть уравнение 
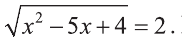Возведем обе части этого уравнения в квадрат, получим равносильное ему уравнение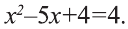 
Ответ: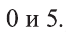 
Уравнение вида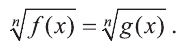 
При решении таких уравнений сначала следует учесть четность-нечетность числа n, а затем привести его к равносильному уравнению.
Пусть n нечётно: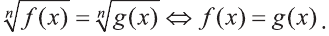 
Например, уравнение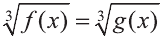 
равносильно уравнению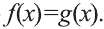 
Пример:
Решите уравнение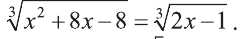 
Решение:
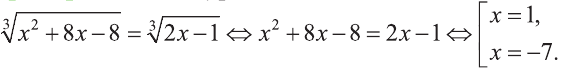
Ответ: 
Пусть n четно, то есть n=2к. В этом случае данное уравнение равносильно каждой из систем: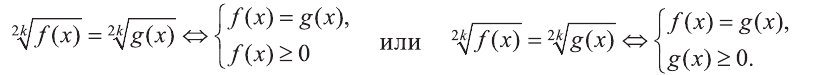 
На практике из данных систем выбирается то, которое легче решается.
Пример:
Решите уравнение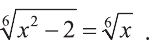 
Решение:
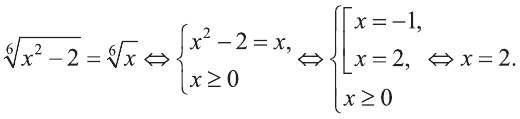
Ответ: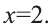 
IV Замена переменных.
Пример:
Решите уравнение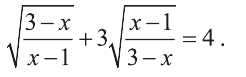 
Решение:
Выполним замену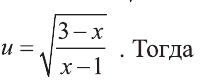 
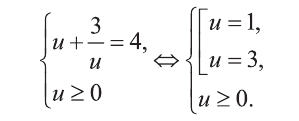
Найдем теперь корни данного уравнения.
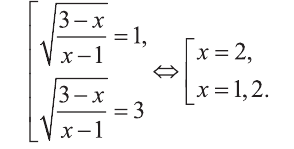
Ответ: х=2 и х=1,2.
Пример:
Решите уравнение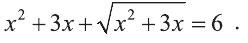 
Решение:
Выполним замену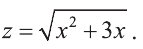 
Тогда
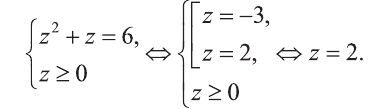
Найдем теперь корни данного уравнения
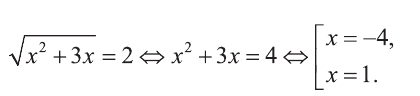
Ответ: х=4 и х=1.
Системы иррациональных уравнений
Решение систем, состоящих из иррациональных уравнений, опирается на известные нам методы сложения, подстановки и т.д. При этом следует учитывать области существования участвующих иррациональных выражений.
Пример:
Решите систему уравнений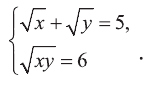 
Решение:
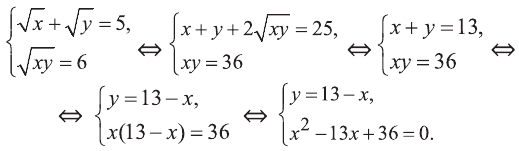
Данная система имеет решения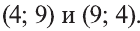 
Пример:
Решите систему уравнений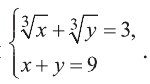 
Решение:
Обозначим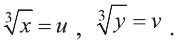 
Воспользовавшись формулой сокращенного умножения, получим систему: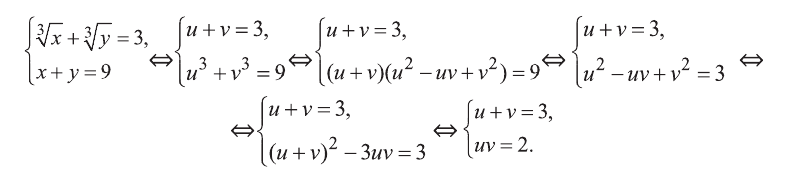 
Эта система имеет решения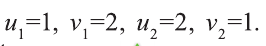 
Отсюда получим решения (1; 8) и (8; 1) исходной системы.
Пример:
Найдите точку С(х; 0), равноудаленную от точек А(3; 4) и В(-2; 5) плоскости.
Решение:
Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение
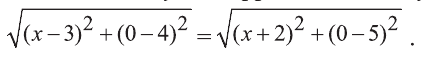
Делая равносильные преобразования, получим уравнение,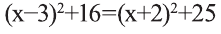
откуда -10х=4. Последнее уравнение имеет корень х=-0,4. Значит, С(-0,4; 0) - искомая точка.
Пример:
Найдите точку на прямой у=3х, равноудаленную от точек А(-1;2) и В(3;—4) плоскости.
Решение:
По условию, ордината и абсцисса искомой точки удовлетворяет соотношению у=3х, поэтому она имеет координаты С(х;3х). Из соотношения АС=ВС и формулы расстояния между двумя точками плоскости получим иррациональное уравнение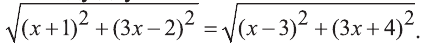 
Делая равносильные преобразования, получим уравнение,
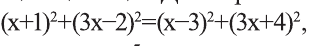откуда -28х=20. Последнее уравнение имеет корень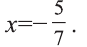 
Значит, С(—5/7; -15/7) - искомая точка. Ответ: С(-5/7; -15/7).
Что называется иррациональным уравнением
Уравнение, содержащее переменную под знаком радикала (или в дробной степени) называется иррациональным уравнением.
Примеры: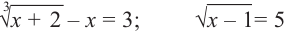 
При решении рациональных уравнений, как правило, применяют возведение в степень. При этом необходимо учитывать следующее:
- решение рационального уравнения ищут на множестве действительных чисел;
- для радикала четной степени берутся арифметические корни, для радикала нечетной степени - действительные значения;
- при возведении обеих частей уравнения в нечетную степень получается равносильное уравнение;
- При возведении в четную степень множество допустимых значений переменной нового уравнения может расширяться. Возможно, что некоторые корни нового уравнения могут не удовлетворять иррациональному уравнению. Поэтому при возведении в четную степень надо проверять, удовлетворяют ли полученные значения переменных заданному иррациональному уравнению.
Пример:
Решите уравнение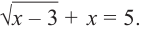 
Решение:
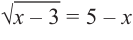Оставим выражение содержащее радикал в
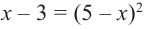одной стороне уравнения возведем обе части
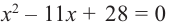уравнения в квадрат, упростим и решим.
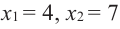
Проверка:
При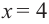 
получаем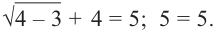 
При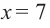 
получаем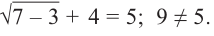 
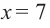не удовлетворяет уравнению.
Ответ: {4}
Отметим, что решить уравнение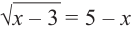 
можно, приведя его к равносильной системе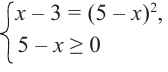 
Определение иррационального уравнения
В этой лекции мы будем рассматривать уравнения, содержащие переменную (неизвестное) под знаком корня (радикала). Такие уравнения называют иррациональными.
Напомним на примерах два из возможных подходов к решению иррациональных уравнений.
Вычисление иррациональных уравнений
Первый подход состоит в замене исходного уравнения равносильным ему уравнением (системой или совокупностью уравнений и неравенств). Поскольку все равносильные уравнения имеют одни и те же решения, то при этом подходе проверка полученных значений переменной по условию исходного уравнения не является необходимой частью решения.
Например, при решении иррациональных уравнений часто пользуются следующими утверждениями о равносильности:
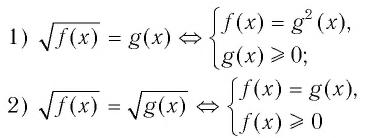
(вместо неравенства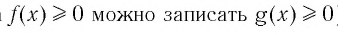 
).
Второй подход состоит в замене исходного уравнения его следствием. Поскольку решений в уравнении-следствии (системе или совокупности) может быть больше, чем в исходном уравнении, то необходимой частью процесса решения является проверка полученных значений переменной по условию исходного уравнения.
Переход к следствию из данного уравнения при оформлении записи решения можно обозначать символом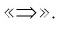
Примеры с решением
Пример №1
Решить уравнение:
Пример №2
Способ 1 (сохранение равносильности).
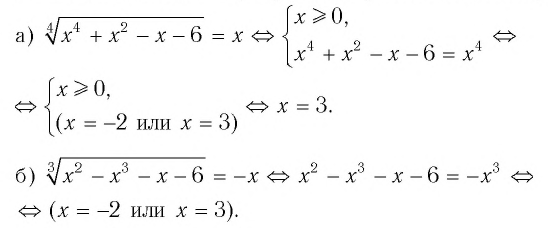
Ответ: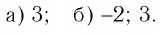
Для уравнения а) покажем решение способом 2 (использование уравнения-следствия):
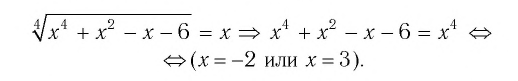
Проверка: при х = -2 получим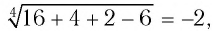 
т. е.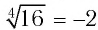
— неверное числовое равенство, значит, число -2 не является корнем уравнения а);
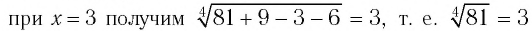— верное числовое равенство, значит, число 3 — корень уравнения а);
Пример №3
Решить уравнение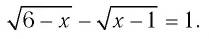 
Решение:
Способ 1 (сохранение равносильности).
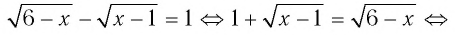
при любых допустимых значениях х обе части уравнения неотрицательны, поэтому, возведя их в квадрат, получим равносильное уравнение
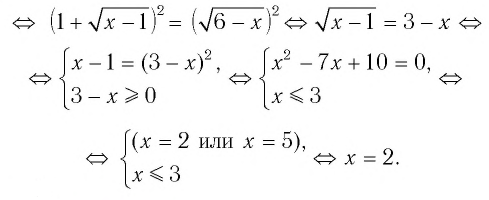
Ответ: 2.
Способ 2 (использование уравнения-следствия).
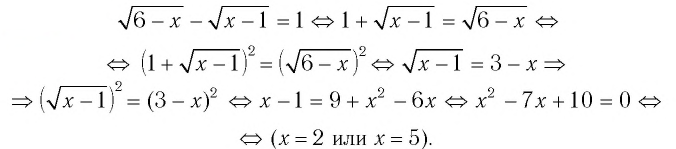
Проверка: х=2 удовлетворяет исходному уравнению, а х=5 не удовлетворяет (убедитесь в этом).
Пример №4
Решить уравнение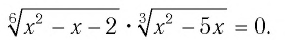
Решение:
Способ 1 (сохранение равносильности).
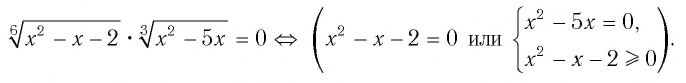
Решив это уравнение и систему, получим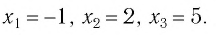 
Ответ: -1; 2; 5.
Способ 2 (использование уравнения-следствия).
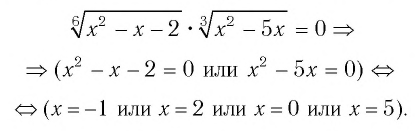
Проверка по условию исходного уравнения показывает, что 0 не является его корнем, так как при х = 0 выражение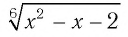 
равно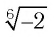 
и не имеет смысла. А числа -1; 2; 5 — являются корнями заданного в условии уравнения.
Пример №5
Решить уравнение с неизвестным х:
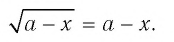
Решение:
Имеем (объясните почему):
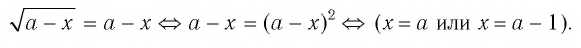
Ответ: при любом значении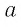 
имеем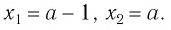 
Пример №6
Решить уравнение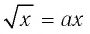 
относительно х.
Решение:
Очевидно, что х = 0 — корень уравнения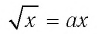
при любом значении а. При х>0 уравнение 
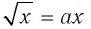равносильно уравнению 
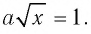Если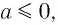 
то это уравнение решений не имеет, а если а > 0, то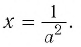 
Ответ: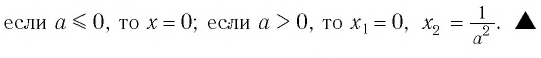 
Решение иррациональных уравнений с использованием свойств функций
Уточним определение уравнения с одной переменной, данное в предыдущих классах.
Пусть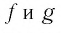 
— функции от переменной 
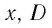— множество всех значений переменной х, при которых определены обе эти функции. Равенство
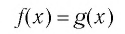
называется уравнением с переменной х, а множество D — областью определения этого уравнения (или областью допустимых значений переменной).
Переменную в уравнении называют также неизвестным. Корнем или решением уравнения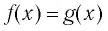 
называется такое число 
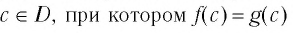— верное числовое равенство.
Теорема:
Уравнение
где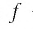 
— возрастающая и 
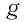— убывающая функции, определенные на одном и том же множестве, имеет не более одного корня, т. е. либо вообще не имеет корней, либо имеет единственный корень.
(Действительно, на рисунке 20, а, б видно, что графики возрастающей функции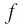
и убывающей функции 
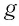пересекаются на области определения не более чем в одной точке.)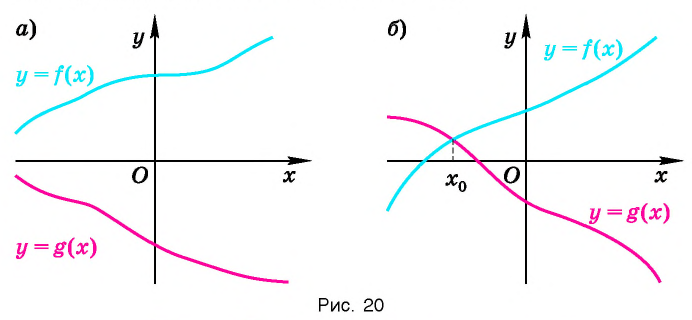 
▲ Доказательство. Пусть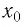 
— корень уравнения (1), т. е.
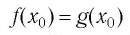— верное числовое равенство.
Если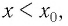
то по определению возрастающей и убывающей функций имеем
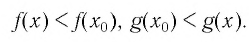
Следовательно,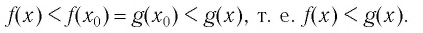
Значит, никакое число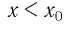 
корнем уравнения (1) не является. Аналогично доказывается, что и никакое число 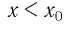не является корнем уравнения (1).
Замечание. Эта теорема справедлива и тогда, когда одна функция возрастающая (убывающая), а другая постоянная.
Приведем несколько примеров, где при решении иррациональных уравнений используются свойства возрастания и убывания функций.
Пример №7
Решить уравнение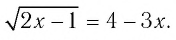
Решение:
Способ 1.
Подбором находим, что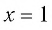 
является корнем данного уравнения. Действительно, 
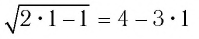— верное числовое равенство.
Так как функция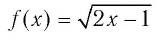 
возрастающая, а функция 
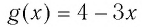убывающая, то согласно теореме 
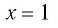— единственный корень данного уравнения.
Ответ: 1.
Способ 2.
Возможно и другое решение:
Так как функция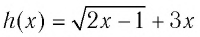 
возрастающая, то (см. замечание) уравнение 
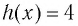имеет не более одного решения. Подбором находим корень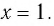 
Пример №8
Решить уравнение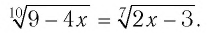 
Решение:
Подбором находим, что число 2 — корень данного уравнения, поскольку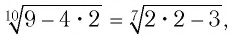 
т. е. 1 = 1 — верное числовое равенство. Других корней уравнение не имеет, так как функция 
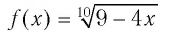является убывающей, а функция 
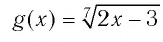— возрастающей.
Ответ: 2.
▲ Иногда при решении иррациональных (и других) уравнений бывает полезно предварительно найти область определения уравнения.
Пример №9
Решить уравнение:
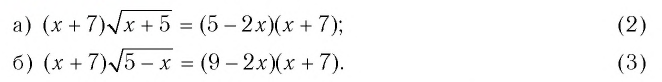
Решение:
а) Значение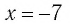 
не принадлежит области определения уравнения (2), поскольку при этом значении выражение 
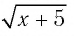не имеет смысла. Поэтому 
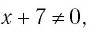и уравнение (2) равносильно уравнению
Решим это уравнение, переходя к уравнению-следствию:
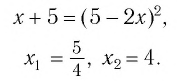
Проверка показывает, что корнем уравнения (4) (а значит, и уравнения (2)) является значение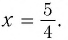 
б) Очевидно, что значение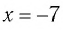 
обращает уравнение (3) в верное числовое равенство и принадлежит области определения уравнения (3) — множеству 
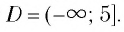Значит, 
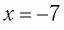— корень уравнения (3).
При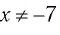 
уравнение (3) равносильно уравнению
Решая это уравнение, получаем:
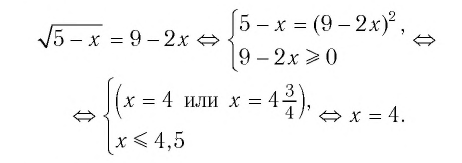
Ответ: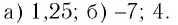 
Решение уравнения (3) с помощью знаков равносильности можно записать так:
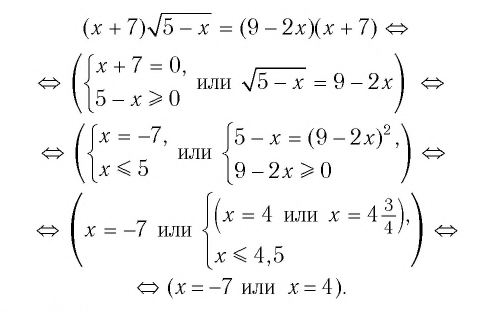
Пример №10
Решить уравнение:
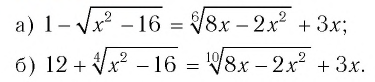
Решение:
а) Поскольку функция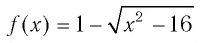 
определена для значений 
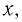удовлетворяющих неравенству 
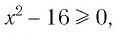а функция 
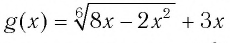определена для значений 
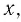удовлетворяющих неравенству 
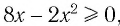то область определения данного уравнения совпадает со множеством решений системы неравенств
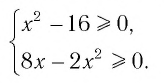
Решая эту систему, получаем равносильную ей систему:
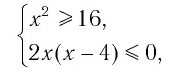
откуда имеем
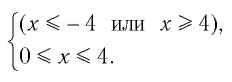
На рисунке 21 видно, что решением этой системы является только значение х = 4. Значит, область определения уравнения состоит из единственного числа 4, т. е.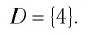 
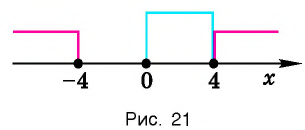
Осталось проверить, является ли число 4 корнем данного уравнения. Подставив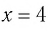 
в исходное уравнение, получим
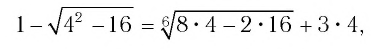
т. е. 1 = 12 — неверное числовое равенство, значит, 4 не является корнем данного уравнения.
б) Решение этого примера аналогично решению примера а). Выполните его самостоятельно.
Ответ: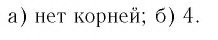 
Пример №11
Решить уравнение
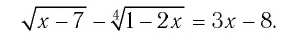
Решение:
Область определения данного уравнения совпадает со множеством решений системы неравенств:
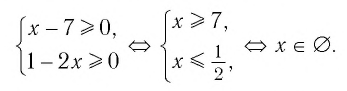Поскольку система не имеет решений, то область определения не содержит ни одного числа. Значит, данное уравнение не имеет корней.
Ответ: нет корней.
Иногда при решении уравнений бывает полезно обратить внимание на наибольшее или наименьшее значения входящих в них функций.
Пример №12
Решить уравнение
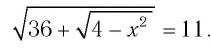
Решение:
Область определения уравнения совпадает со множеством решений неравенства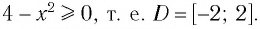 
Очевидно, что функция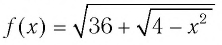 
имеет наибольшее значение 
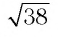при х = 0. Таким образом, при любых значениях 
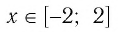верно неравенство 
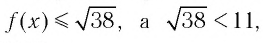поэтому данное уравнение решений не имеет.
Ответ: нет решений. ▲
Напомним:
Уравнения, содержащие переменную под знаком корня, называются иррациональными.
При решении иррациональных уравнений не всегда удается от данного уравнения перейти к равносильному ему уравнению.
Например, решим уравнение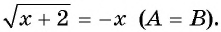 
Первый способ.
Возведем обе части уравнения в квадрат, получим уравнение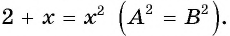 
Оно имеет корни 
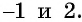Очевидно, что число 2 не является корнем данного уравнения, так как 
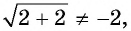а число 
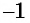— корень данного уравнения, так как равенство 
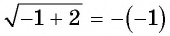является верным.
Посторонний корень уравнения (число 2) появился оттого, что уравнение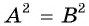 
равносильно совокупности уравнений 
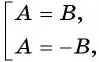которая может иметь больше решений, чем данное уравнение 
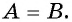Поэтому после возведения обеих частей уравнения в четную степень без дополнительных условий следует выполнять проверку полученных корней.
Второй способ.
Уравнение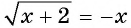 
равносильно системе 
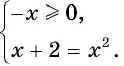Действительно, обе части уравнения неотрициональны, поэтому при возведении в квадрат получим:
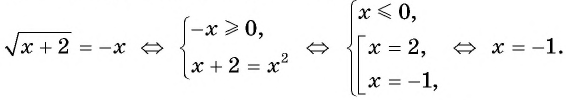
Третий способ.
Запишем уравнение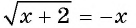 
в виде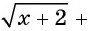 
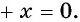Рассмотрим функцию 
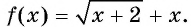Эта функция возрастает на области определения, значит, данное уравнение не может иметь больше одного корня. Анализируя условие, заметим, что корень должен быть отрицательным и не превосходить по модулю число 2. Корнем данного уравнения является число -1.
Рассмотрим некоторые виды иррациональных уравнений и методы их решения.
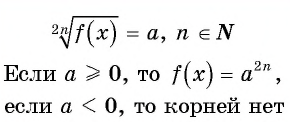
Уравнение вида=2n√f(x), где n∈N
Уравнение вида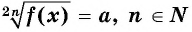 
Есл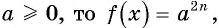и 
если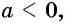 
то корней нет.
Пример №13
Решите уравнение:
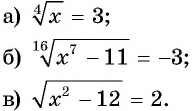
Решение:
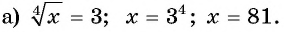
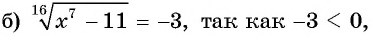то уравнение не имеет корней.
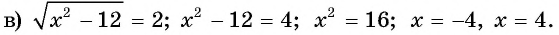
Ответ а) 81; б) нет корней; в) -4; 4.
Уравнение вида 2n+1√f(x)=a, где n∈N
Уравнение вида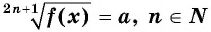 
Уравнение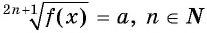 
равносильно уравнению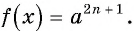 
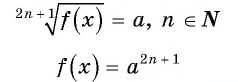
Пример №14
Решите уравнение:
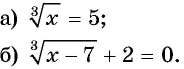
Решение:
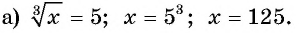
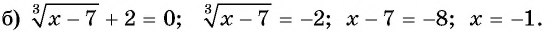
Ответ а) 125; б) -1.
Уравнение вида m√f(x)=g(x), m∈N, m>1
Уравнение вида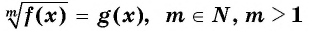 
Пусть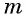 
— четное число.
Рассмотрим способы решения уравнения вида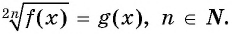 
Первый способ.
Данное уравнение равносильно системе
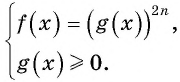
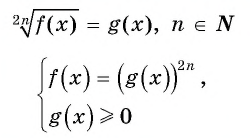
Пример №15
Решите уравнение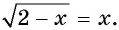 
Решение:
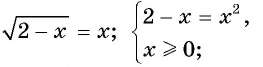
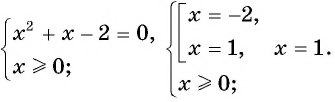Ответ: 1
Второй способ.
Уравнение данного вида можно решить, возведя обе части уравнения в степень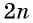 
с последующей проверкой корней.
Пример №16
Решите уравнение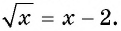 
Решение:
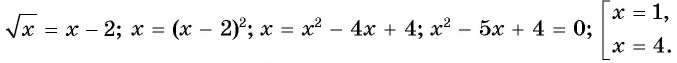
Проверка: при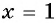 
равенство 
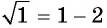неверное; при 
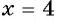равенство 
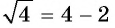верное. Ответ: 4.
Если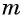 
— нечетное число, то уравнение вида 
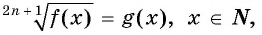равносильно уравнению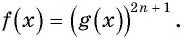 
Пример №17
Решите уравнение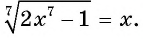 
Решение:
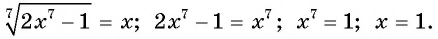
Ответ: 1.
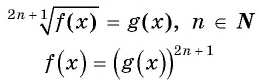
Уравнение вида m√f(x)=m√g(x), m∈N, m>1
Уравнение вида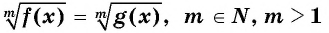 
Пусть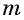 
— четное число.
Рассмотрим способы решения уравнения вида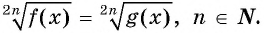 
Первый способ.
Данное уравнение равносильно одной из систем
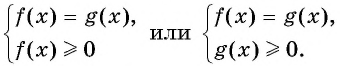
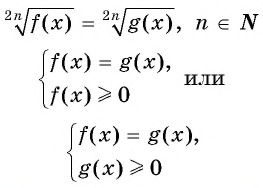
Пример №18
Решите уравнение
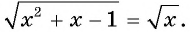
Решение:
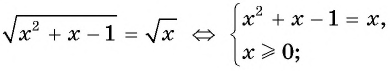
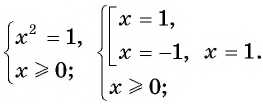
Ответ: 1
Второй способ.
Уравнение этого вида можно решить, возведя обе части уравнения в степень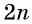 
с последующей проверкой корней.
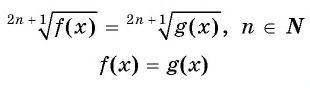
Пример №19
Решите уравнение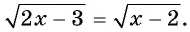 
Решение:
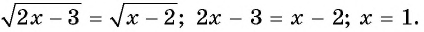
Проверка: при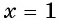 
выражения в левой и правой частях равенства 
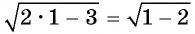не имеют смысла, т. е. исходное уравнение не имеет корней.
Ответ: нет корней.
Если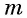 
— нечетное число, то уравнение вида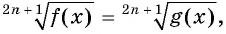 
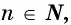равносильно уравнению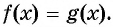 
Пример №20
Решите уравнение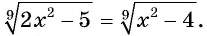 
Решение:
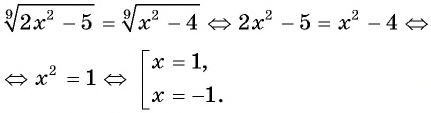
Уравнение вида √f(x)±√g(x)=a
Уравнение вида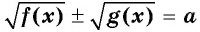 
Первый способ.
Уравнение вида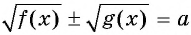 
можно решить, возведя обе части уравнения в квадрат дважды с последующей проверкой найденных корней.
Пример №21
Решите уравнение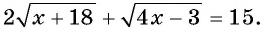 
Решение:
Перенесем одно из слагаемых в правую часть, для того чтобы сократить преобразования.
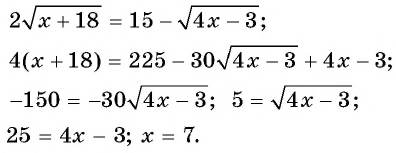
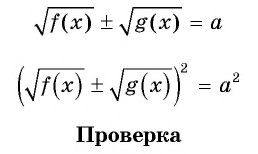
Проверка: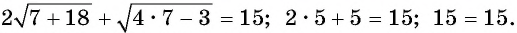 
Значит, значение 
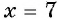является корнем уравнения.
Ответ: 7.
Второй способ.
Некоторые уравнения этого вида можно решить, используя свойства функций.
Пример №22
Решите уравнение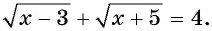 
Решение:
Функция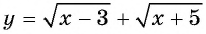 
возрастает на всей области определения, поэтому, если данное уравнение имеет корень, то только один.
При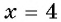 
данное уравнение обращается в верное числовое равенство: 
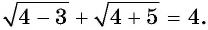Значит, число 4 является единственным корнем данного уравнения.
Ответ: 4.
Метод замены переменной
Пример №23
Решите уравнение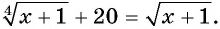 
Решение:
Пусть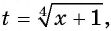 
тогда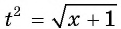 
и уравнение принимает вид 
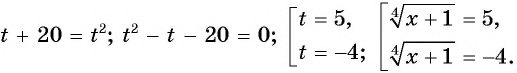Второе уравнение совокупности не имеет корней.
Тогда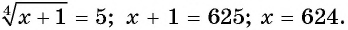 
Ответ: 624.
Пример №24
Решите уравнение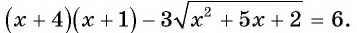 
Решение:
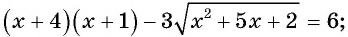
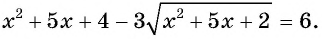
Пусть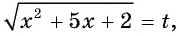 
тогда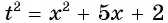 
и уравнение принимает вид 
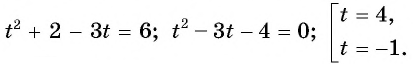Так как 
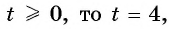т.е.
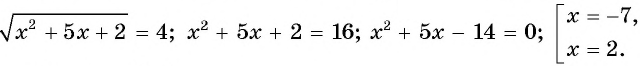
Ответ: -7; 2.
Примеры заданий и их решения
Пример №25
Решите уравнение:
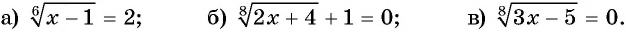
Решение:
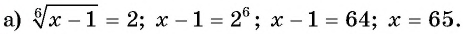
Ответ. 65.
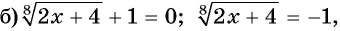так как 
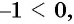то уравнение не имеет корней.
Ответ: нет корней.
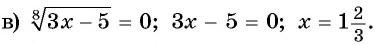
Ответ: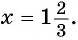 
Пример №26
Решите уравнение:
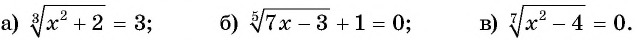
Решение:
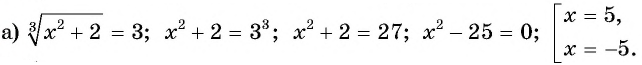
Ответ: -5; 5.
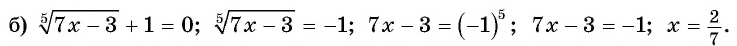
Ответ: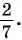 
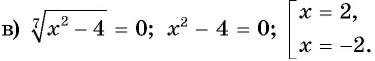
Ответ. -2; 2.
Пример №27
Решите уравнение:
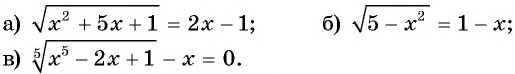
Решение:
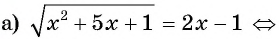
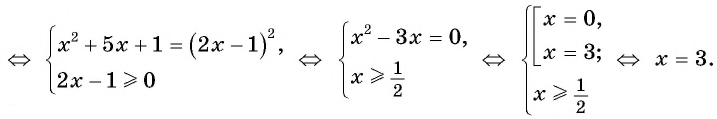
Ответ: 3.
б) Возведем обе части уравнения в квадрат и получим:
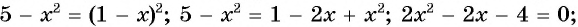
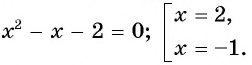
Проверка: при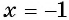 
получим: 
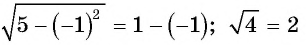— верное равенство, значит, 
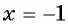— корень данного уравнения. При 
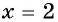имеем: 
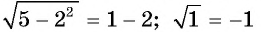— неверное равенство, значит, 
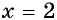не является корнем данного уравнения.
Ответ: -1.
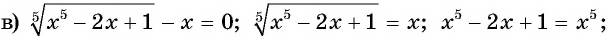
Ответ: 0,5.
Пример №28
Решите уравнение:
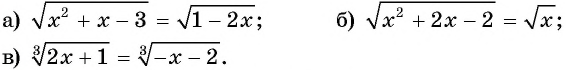
Решение:
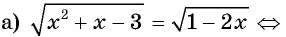
Ответ: -4.
б) Возведем обе части уравнения в квадрат и получим:
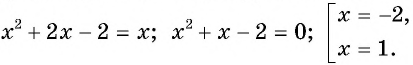
Проверка: при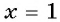 
получим: 
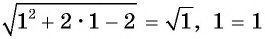— верно, значит, 
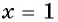— корень данного уравнения. При 
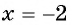выражение 
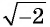не имеет смысла, т. е. 
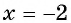не является корнем данного уравнения.
Ответ: 1.
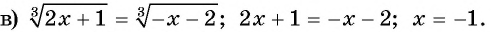
Ответ: -1
Пример №29
Решите уравнение: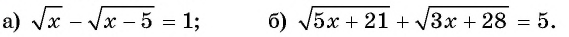 
Решение:
а) Запишем уравнение в виде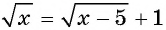 
и возведем обе части полученного уравнения в квадрат: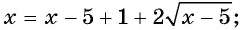 
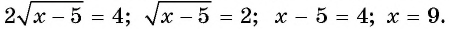С помощью проверки убедимся, что 
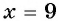является корнем исходного уравнения.
Ответ: 9.
б) Функция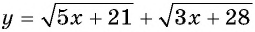 
возрастает на всей области определения, поэтому если данное уравнение имеет корень, то только один.
При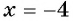 
данное уравнение обращается в верное числовое равенство: 
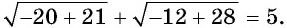Значит, число 
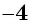является единственным корнем данного уравнения.
Ответ: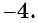 
Пример №30
Решите уравнение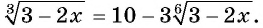 
Решение:
Пусть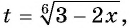 
тогда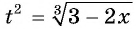 
и исходное уравнение принимает вид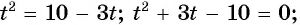 
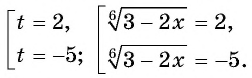
Второе уравнение совокупности не имеет корней. Тогда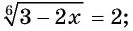 
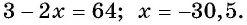
Ответ.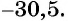 
При решении иррациональных уравнений используют прием возведения левой и правой частей уравнения в одну степень.
Теорема 9.
Возведение левой и правой частей уравнения в нечетную натуральную степень дает уравнение, равносильное данному, а возведение в четную степень — уравнение, являющееся следствием данного уравнения.
Доказательство:
Пусть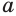 
— корень уравнения 
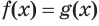. Тогда истинно числовое равенство 
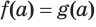. Возведя его в степень 
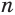, по соответствующему свойству числовых равенств получим равенство 
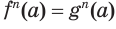, которое также истинно. А это означает, что число 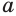— корень уравнения 
.
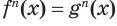Поскольку каждый корень уравнения 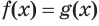является корнем уравнения 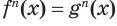, то из уравнения 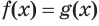следует уравнение .
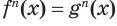Пусть 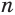— нечетное натуральное число и 
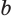— корень уравнения 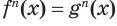. Тогда истинно числовое равенство 
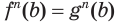. Извлекая из обеих его частей корень степени 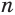, по соответствующему свойству числовых равенств получим числовое равенство 
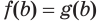, которое истинно. Значит, число 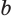— корень уравнения .
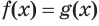Поскольку при нечетном натуральном 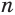из уравнения 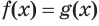следует уравнение 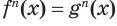и из уравнения 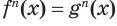следует уравнение 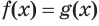, то эти уравнения равносильны.
Пример №31
Решим уравнение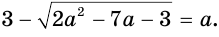 
Данное уравнение равносильно уравнению 
. Возведем обе его части в квадрат и приведем подобные:
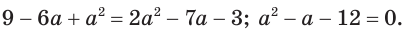
Полученное квадратное уравнение имеет корнями числа -3 и 4. Сделаем проверку. Подставив числа -3 и 4 в данное уравнение, получим числовые равенства
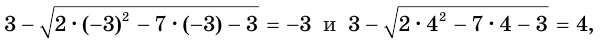
из которых истинно только первое равенство.
Ответ. -3.
Этот пример иллюстрирует ту часть теоремы 9, в которой утверждается, что возведение в четную степень обеих частей уравнения дает уравнение, которое является следствием данного уравнения. Появление постороннего корня 4 связано с тем, что возведением в квадрат к уравнению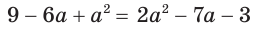 
приводит не только данное уравнение, но и уравнение 
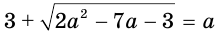, которое и имеет корнем число 4.
Вообще, при решении уравнений нужно быть внимательным к выполняемым преобразованиям. Полученные в результате решения числа включаются в ответ только в случае, когда все преобразования были преобразованиями равносильности.
Пример №32
Решим уравнение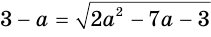 
, используя только преобразования равносильности:
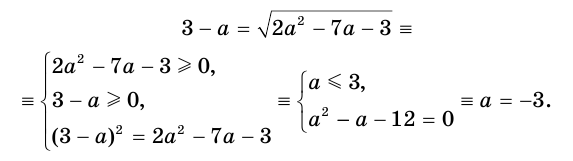
Некоторые иррациональные уравнения могут быть решены приемом введения вспомогательных переменных.
Пример №33
Решим уравнение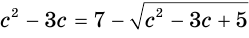 
.
Обратим внимание на то, что данное уравнение равносильно уравнению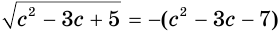 
, в котором выражение 
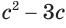повторяется. Это наводит на мысль, что его или выражение, его содержащее, целесообразно рассматривать в качестве новой переменной. Обозначим через 
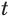, например, выражение 
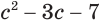, т. е.
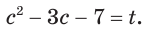
Тогда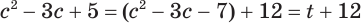 
.
Это позволяет данное уравнение заменить уравнением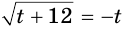 
. Решим его:
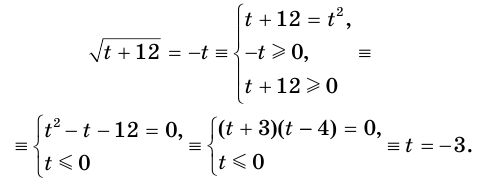
Вернемся к исходной переменной:
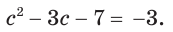
Полученное уравнение имеет корнями числа -1 и 4. Они и являются корнями исходного уравнения.
Ответ. -1; 4.
Иногда бывает удобно ввести две вспомогательные переменные.
Пример:
Решим уравнение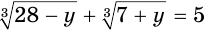 
.
Обозначим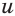 
и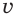 
первый и второй радикалы соответственно:
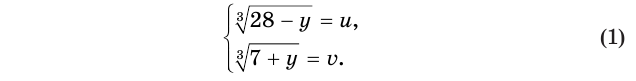
Тогда данное уравнение запишется как
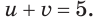
Из системы (1) получим еще одно уравнение, связывающее переменные 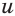и :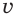
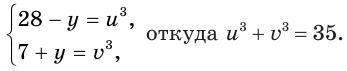
Таким образом, для нахождения значений переменных 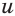и 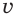получилась система 
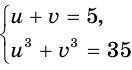, которая решается так:
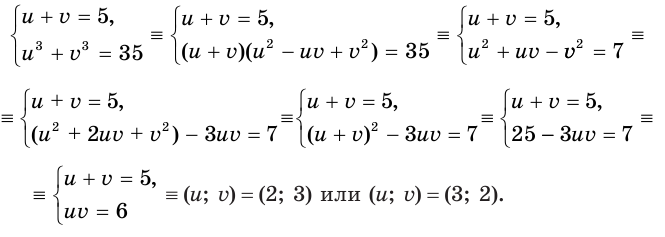
Теперь, чтобы найти значения исходной переменной, достаточно решить любое из уравнений системы (1).
Для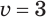 
, а затем для 
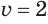получим соответственно:
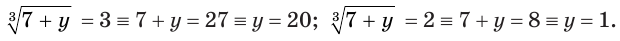
Анализ выполненных преобразований показывает, что все они являются преобразованиями равносильности. Поэтому оба полученных значения переменной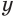 
являются корнями данного уравнения.
Ответ. 1; 20.
Пример №34
Решим систему уравнений
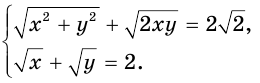
Обозначим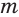 
и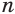 
соответственно сумму и произведение радикалов 
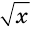и 
:
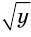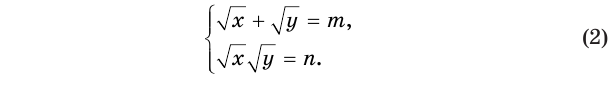
Выразим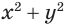 
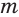через и 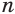. Получим:
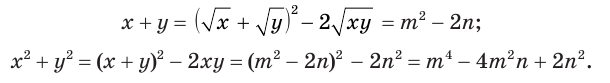
С учетом этого исходная система запишется так:
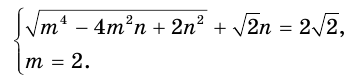
Поскольку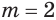 
, то первое уравнение системы приводится к уравнению 
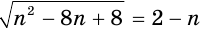, решив которое, получим 
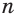= 1.
Учитывая, что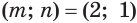
, из системы (2) находим, что 
.
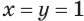Ответ. (1; 1).
Иногда при решении системы бывает полезна тригонометрическая подстановка.
Пример №35
Решим систему уравнений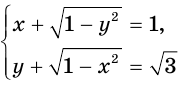 
.
Обратим внимание на то, что модули переменных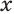 
и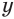 
не превышают 1. Поэтому можно ввести вспомогательные переменные 
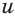и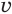 
:
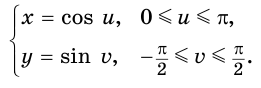
Выразим через них исходную систему и найдем ее решения:
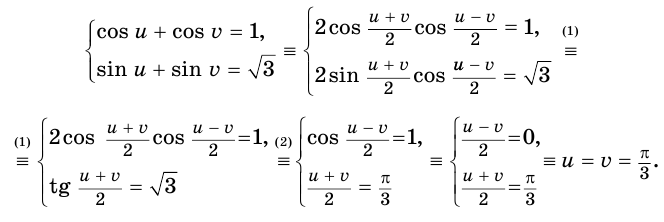
При переходе (1) мы покомпонентно второе уравнение разделили на первое, при переходе (2) учли то, что поскольку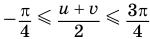 
, то уравнение 
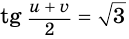имеет корнем число 
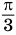, но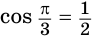 
, поэтому первое уравнение записывается в виде 
.
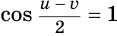Вернувшись к исходным переменным, получим, что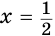 
и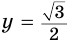 
.
Ответ.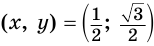 
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |