
Иррациональные неравенства с примерами решения
Неравенства, содержащие переменную под знаком радикала, называются иррациональными неравенствами.
Содержание:
Решение иррациональных неравенств также ищут на множестве действительных чисел и, используя свойства корня и неравенств, сводится к решению системы рациональных неравенств.
Пример: Решите неравенство 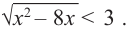
Решение: чтобы найти множество решений данного неравенства на множестве допустимых значений, т. е. при условии 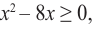
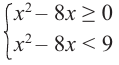
Каждое неравенство системы решим методом интервалов и найдем пересечение полученных решений:
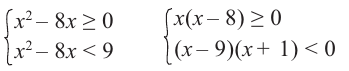
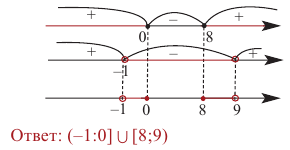
Пример: Решите неравенство 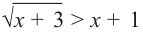
Решение: рассмотрим два случая, в зависимости от знака правой части.
1) при 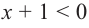 для всех
для всех 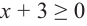 неравенство справедливо для всех
неравенство справедливо для всех 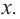 Значит, надо решить систему
Значит, надо решить систему
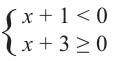
Ее решением является промежуток 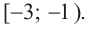
2) при 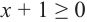 обе стороны заданного неравенства можно возвести в квадрат. Тогда получим систему
обе стороны заданного неравенства можно возвести в квадрат. Тогда получим систему
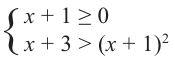
Ее решением является промежуток 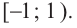
Решением заданного неравенства является 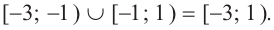
Способы решения иррациональных неравенств
С действием возведения в степень связаны разные виды выражений. Будем рассматривать выражения с переменными, при образовании которых используются действия сложения, вычитания, умножения, деления и возведения в степень, причем возведение в степень хотя бы один раз применено к выражению с переменной.
Если показатель степени целый, то возникает рациональное выражение, если дробный, то — иррациональное выражение, а если иррациональный, то — трансцендентное выражение.
К трансцендентным выражениям приводят и действия нахождения значений синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса, арккотангенса. Рациональные и иррациональные выражения вместе составляют множество алгебраических выражений.
Из выражений
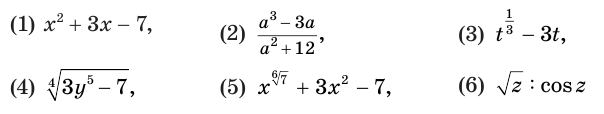
выражения (1) и (2) являются рациональными, выражения (3) и (4) — иррациональными, выражения (5) и (6) — трансцендентными, а выражения (1)—(4) — алгебраическими.
В зависимости от того, из каких выражений составлено уравнение, говорят о рациональных, иррациональных, трансцендентных уравнениях.
Из уравнений
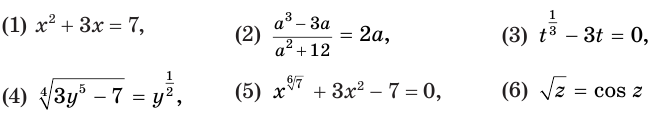
уравнения (1) и (2) являются рациональными, уравнения (3) и (4) — иррациональными, а уравнения (5) и (6) — трансцендентными.
Так же говорят о рациональных, иррациональных, трансцендентных неравенствах.
В этом параграфе рассматривается решение иррациональных уравнений и неравенств. При их решении нужно следить за тем, какие преобразования выполняются при этом.
Утверждение 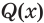 равносильно утверждению
равносильно утверждению 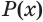 , если утверждения
, если утверждения 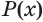 и
и 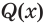 истинны при одних и тех же значениях переменной
истинны при одних и тех же значениях переменной 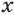 . Равносильность уравнений означает, что они имеют одни и те же корни, а равносильность неравенств — то, что они имеют одни и те же решения. Равносильность утверждений
. Равносильность уравнений означает, что они имеют одни и те же корни, а равносильность неравенств — то, что они имеют одни и те же решения. Равносильность утверждений 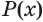 и
и 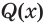 обозначают
обозначают 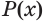 =
= 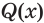 .
.
Утверждение 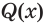 следует из утверждения
следует из утверждения 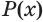 , если утверждение
, если утверждение 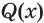 истинно при всех значениях переменной
истинно при всех значениях переменной 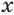 , при которых истинно утверждение
, при которых истинно утверждение 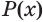 . Следование второго уравнения из первого означает, что каждый корень первого уравнения является корнем второго уравнения, но второе уравнение может иметь и дополнительные корни. Так же понимается и следование одного неравенства из другого. Следование утверждения
. Следование второго уравнения из первого означает, что каждый корень первого уравнения является корнем второго уравнения, но второе уравнение может иметь и дополнительные корни. Так же понимается и следование одного неравенства из другого. Следование утверждения 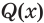 из утверждения
из утверждения 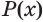 обозначают
обозначают  .
.
Отношения равносильности и следования связаны:
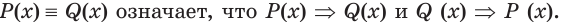
При решении иррациональных неравенств нужно учитывать, что проверка подстановкой найденного множества чисел обычно невозможна из-за его бесконечности. Поэтому при решении неравенств нужно следить за равносильностью проводимых преобразований.
Теорема:
Верны следующие равносильности:
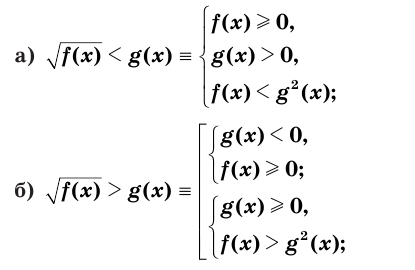
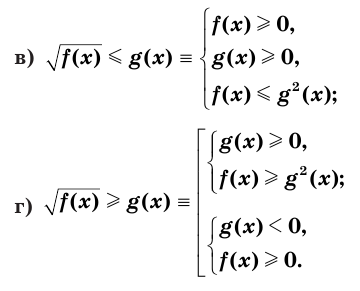
Доказательство проводится по схеме, использованной при доказательстве теоремы 9 с применением соответствующих свойств числовых неравенств.
Пример №1
Решим неравенство 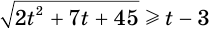 . Это неравенство равносильно совокупности неравенств
. Это неравенство равносильно совокупности неравенств
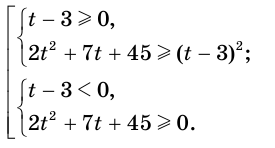
Первую систему можно заменить равносильной системой 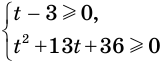 , которая равносильна системе
, которая равносильна системе  , которая, в свою очередь, равносильна неравенству
, которая, в свою очередь, равносильна неравенству  .
.
Вторая система совокупности равносильна системе 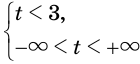 , которая равносильна неравенству
, которая равносильна неравенству 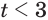 .
.
Решения данного неравенства получим, когда объединим решения  и
и 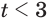 первой и второй систем совокупности, в результате получим множество всех действительных чисел.
первой и второй систем совокупности, в результате получим множество всех действительных чисел.
Ответ. 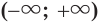 .
.
Пример №2
Решим неравенство 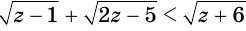 .
.
Обратим внимание на то, что на области определения левая и правая части данного неравенства обе неотрицательны, поэтому оно равносильно системе неравенств
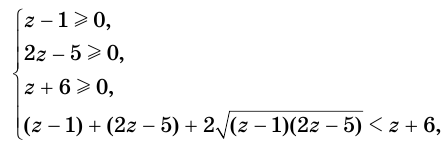
решение которой следующее:
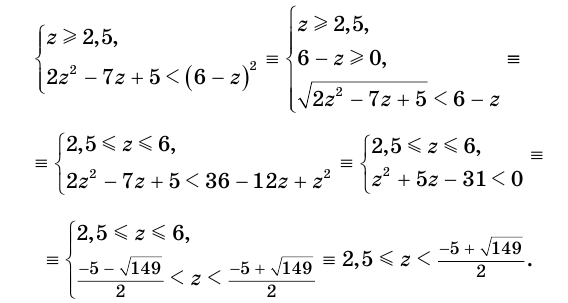
Ответ. 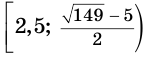 .
.
Какие неравенства называются иррациональными
В этой лекции мы будем рассматривать неравенства, содержащие переменную (неизвестное) под знаком корня. Такие неравенства называются иррациональными.
При решении иррациональных неравенств часто используют подход, который мы уже применяли, решая иррациональные уравнения. Он состоит в замене исходного неравенства равносильным ему неравенством (системой или совокупностью неравенств).
Пример №3
Решить неравенство:

Решение:
а) Учитывая свойства корня нечетной степени, получаем:
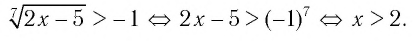
б) По определению корня четной степени значения выражения
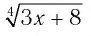 неотрицательны при всех значениях
неотрицательны при всех значениях 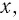 при которых это
при которых это
выражение имеет смысл, т. е. когда значения подкоренного выражения неотрицательны. Таким образом, имеем:
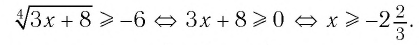
Ответ: 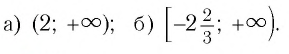
Пример №4
Решить неравенство:

Решение:
а) По определению корня четной степени значения выражения 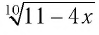 отрицательными быть не могут. Поэтому имеем:
отрицательными быть не могут. Поэтому имеем:
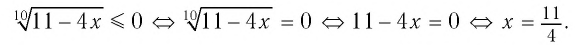
б) Поскольку обе части неравенства 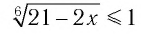 неотрицательны при всех значениях
неотрицательны при всех значениях 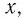 при которых его левая часть имеет смысл, то имеем:
при которых его левая часть имеет смысл, то имеем: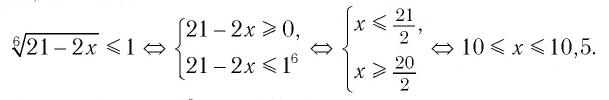
Ответ: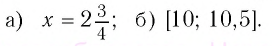
При решении иррациональных неравенств часто используется также метод интервалов.
Пример №5
Решить неравенство 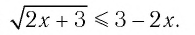
Решение:
Обозначим 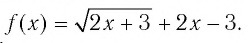 Найдем область определения функции
Найдем область определения функции 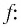
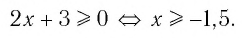
Таким образом, 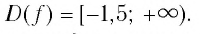
Найдем нули функции 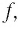 т. е. корни уравнения
т. е. корни уравнения 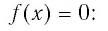
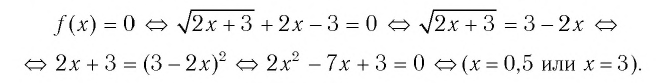
Проверка: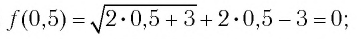
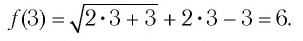
Значит, 0,5 — единственный нуль функции 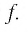
Отметим нуль функции 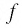 на области определения
на области определения 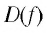 (рис.22). Определим знаки значений функции
(рис.22). Определим знаки значений функции 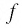 на образовавшихся интервалах, для чего вычислим:
на образовавшихся интервалах, для чего вычислим:
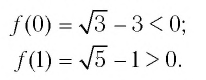
Используя рисунок 22, запишем решение неравенства 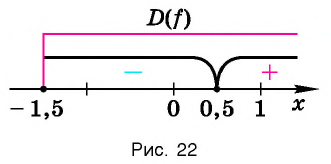
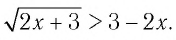
Ответ: 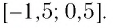
Пример №6
Решить неравенство 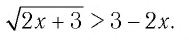
Решение:
Решение этого примера аналогично решению примера 3.
Используя рисунок 22, записываем решение неравенства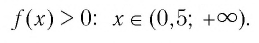
Ответ: 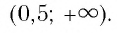
▲ При решении иррациональных неравенств часто используются следующие утверждения о равносильности неравенств и систем неравенств:
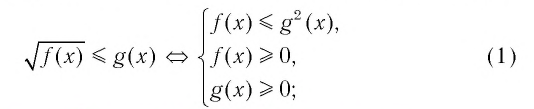
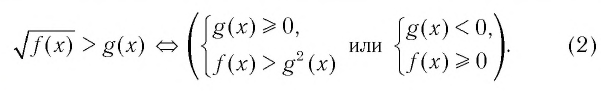
Решим пример 3, используя равносильность (1):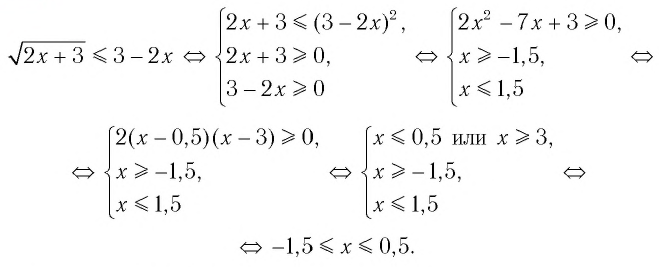
Ответ: 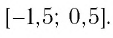
Решим пример 4, используя равносильность (2):
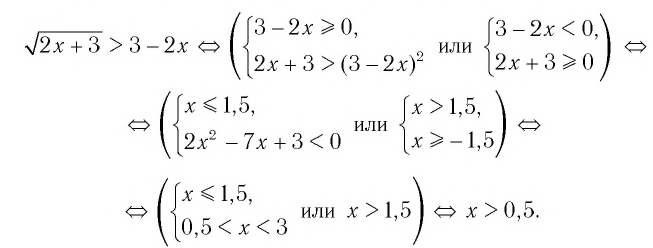
Ответ: 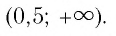
Для решения заданий такого типа, как, например, в 1.265, можно использовать следующие утверждения о равносильности:
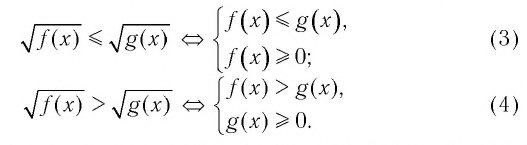
Аналогичные утверждения можно записать и для неравенств 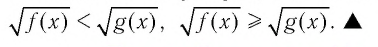
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Производная в математике
- Как найти производную функции
- Асимптоты графика функции
- Касательная к графику функции и производная
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Иррациональные уравнения