
Интегрирование рациональных дробей с примерами решения
Содержание:
Интегрирование рациональных дробей
Полиномы. Разложение полиномов на простые множители
Напомним, что полиномом n-ой степени называется выражение вида 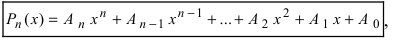
Теорема: (теорема Безу) Если полином степени n разделить на выражение 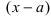 , то остаток деления будет равен
, то остаток деления будет равен 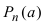 .
.
Доказательство: Пусть 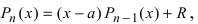 где R - остаток деления. Полагая
где R - остаток деления. Полагая 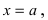 получим
получим 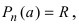 следовательно,
следовательно, 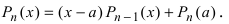
Следствие: Если а является корнем уравнения 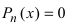 , то остаток деления равен нулю, т.е.
, то остаток деления равен нулю, т.е. 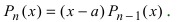
Рассмотрим основные теоремы алгебры.
Теорема: Любой полином степени n имеет хотя бы один корень (действительный или мнимый).
Теорема: (о разложении полинома на простые множители) Любой полином степени n можно представить в виде произведения коэффициента при старшей степени 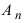 на n множителей вида
на n множителей вида 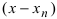 , где хп
, где хп 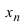 - корни уравнения
- корни уравнения 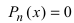 , т.е.
, т.е.
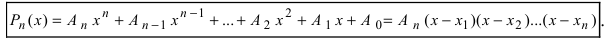
Доказательство: Воспользуемся следствием из теоремы Безу: 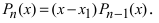 Поступая аналогично, найдем, что
Поступая аналогично, найдем, что
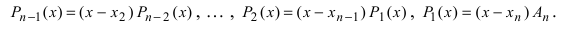
Пример:
Разложить на простые множители полином 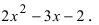
Решение:
Найдем корни уравнения 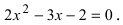 Дискриминант уравнения
Дискриминант уравнения 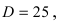 следовательно,
следовательно, 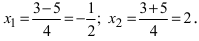 Таким образом, разложение полинома на простые множители имеет вид:
Таким образом, разложение полинома на простые множители имеет вид: 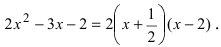
Теорема: Если 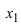 является комплексным корнем полинома
является комплексным корнем полинома 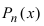 , то комплексно-сопряженное число
, то комплексно-сопряженное число 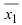 также является корнем этого полинома.
также является корнем этого полинома.
Пример:
Найти корни полинома 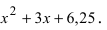
Решение:
Найдем корни уравнения 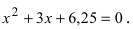 Дискриминант уравнения
Дискриминант уравнения 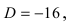 следовательно,
следовательно, 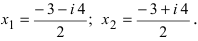 Отсюда видно, что
Отсюда видно, что 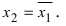
Замечание: Из данного примера видно, что комплексно-сопряженные корни представляются в разложении полинома на простые множитет в виде квадратных многочленов с отрицательными дискриминантами.
Определение: Если корень а повторяется в разложении полинома на простые множители 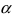 раз, то он называется кратным корнем или корнем кратности
раз, то он называется кратным корнем или корнем кратности 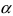 .
.
Пример:
Разложить на простые множители полином 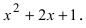
Решение:
Данный полином представляет собой полный квадрат, поэтому после сворачивания он принимает вид 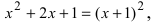 т.е. корень х = -1 является корнем кратности 2.
т.е. корень х = -1 является корнем кратности 2.
Интегрирование рациональных дробей
Метод неопределенных коэффициентов
Определение: Отношение двух полиномов 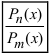 называется рациональной дробью. Если
называется рациональной дробью. Если 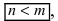 то дробь называется правильной, а в случае, когда
то дробь называется правильной, а в случае, когда 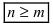 - неправильной.
- неправильной.
Пример:
Выяснить, какие дроби являются правильными, а какие - неправильными: а)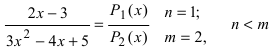 - правильная рациональная дробь; б)
- правильная рациональная дробь; б)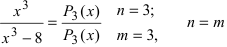 - неправильная рациональная дрооь; в)
- неправильная рациональная дрооь; в) 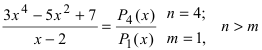 неправильная рациональная дробь.
неправильная рациональная дробь.
Решение:
Если рациональная дробь неправильная, то можно выделить “целую” часть так же, как и в случае обычной неправильной дроби: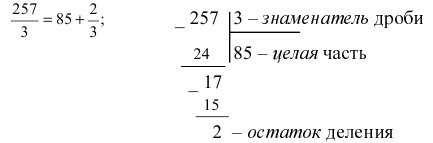
При делении полинома на полином надо обращать внимание на старшие степени этих полиномов и числовые множители при них. В качестве примера выделения “целой" части у неправильной дроби рассмотрим отношение
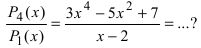
Итак, 
Таким образом, можно записать, что 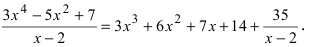
Замечание: Деление числителя на знаменатель дроби прекращается тогда, когда в остатке деления получается полином, порядок которого становится меньше порядка полинома, стоящего в знаменателе.
Интегрирование рациональных дробей проводится по следующей методической схеме: Если рациональная дробь неправильная, то выделяют “целую" часть, которая легко интегрируется (интегралы от “целой" части являются табличными (см. таблицу неопределенных интегралов от степенной функции в Лекции № 1, Второго семестра)) и правильную рациональную дробь, интегрирование которой проводится следующим образом (покажем схему на конкретном примере):
Пример:
Вычислить 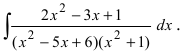
Решение:
1. Знаменатель правильной рациональной дроби раскладывают на простые множители.
В данном примере надо разложить на простые множители полином 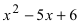 По теореме Виета корнями уравнения
По теореме Виета корнями уравнения 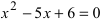 будут
будут 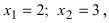 следовательно,
следовательно, 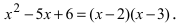 Полином
Полином 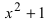 имеет комплексные корни, поэтому он является простым сомножителем.
имеет комплексные корни, поэтому он является простым сомножителем.
2. Правильная рациональная дробь раскладывается на сумму простых дробей, число которых равно числу простых сомножителей в разложении знаменателя дроби на простые множители
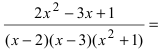 = (для данной дроби имеем три простых сомножителя, следовательно, будет три простых дроби)
= (для данной дроби имеем три простых сомножителя, следовательно, будет три простых дроби)
3. В знаменатели простых дробей пишут один из простых множителей знаменателя правильной рациональной дроби:
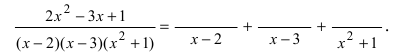
4. В числитель простой дроби пишут папином с неизвестными коэффициентами, степень которого на единицу ниже, чем степень полинома, стоящего в знаменателе простой дроби
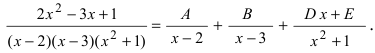
Замечание: В случае кратных корней количество простых дробей определяется кратностью корня, причем в знаменатели простых дробей записывается кратный корень с увеличением его степени на единицу, пока не будет достигнута кратность корня. Степень полинома для всех этих дробей, который записывается в числитель простой дроби определяется по первой степени кратного корня. Например,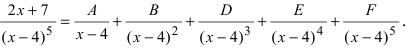
Замечание: Литеру С использовать не рекомендуется, так как она задействована в роли постоянной интегрирования.
5. Сумма простых дробей приводится к общему знаменателю и числитель получившейся дроби приравнивается к числителю исходной дроби
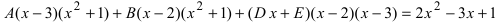 или
или
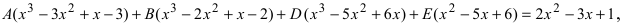 или после раскрытия скобок и приведения подобных членов получаем
или после раскрытия скобок и приведения подобных членов получаем
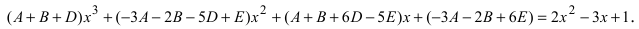
6. Сравнивая коэффициенты при одинаковых степенях переменной величины х в левой и правой частях равенства, получают систему линейных алгебраических уравнений (СЛАУ) относительно неизвестных коэффициентов А, В,
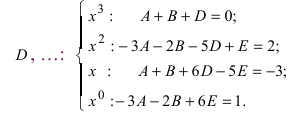
Замечание: Если разложение полинома, стоящего в знаменателе дроби, на простые множители содержит не кратные действительные корни, то процедура отыскания неопределенных коэффициентов упрощается путем подстановки в левую и правую части равенства значений корней, например,
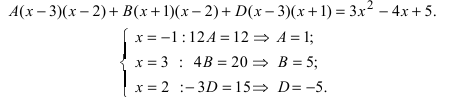
7. Решают СЛАУ и находят числовые значения неизвестных коэффициентов А, В, D, ... Для рассматриваемого примера 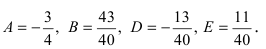
8. Числовые значения неопределенных коэффициентов подставляют в разложение правильной рациональной дроби на простые дроби (п.4 данной схемы)
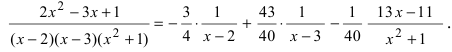
9. Полученное разложение рациональной дроби на простые дроби интегрируется 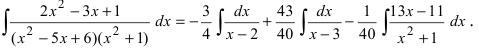
Пример:
Вычислить 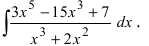
Решение:
Подынтегральная функция представляет собой неправильную рациональную дробь, поэтому выделим "целую" часть и правильную рациональную дробь: 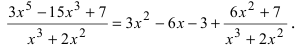 Разложив знаменатель правильной рациональной дроби на простые множители, представим эту дробь в виде суммы простых дробей:
Разложив знаменатель правильной рациональной дроби на простые множители, представим эту дробь в виде суммы простых дробей: 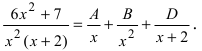 Приводя сумму простых дробей к общему знаменателю и приравнивая числитель получившейся дроби к числителю исходной дроби, получим после раскрытия скобок и приведения подобных членов:
Приводя сумму простых дробей к общему знаменателю и приравнивая числитель получившейся дроби к числителю исходной дроби, получим после раскрытия скобок и приведения подобных членов:
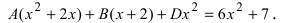
Сравнивая коэффициенты при одинаковых степенях х, получаем СЛАУ: 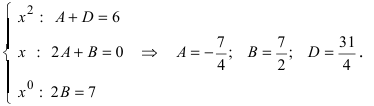
Таким образом, подынтегральную функцию можно представить в виде: 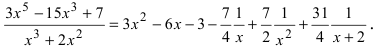 Проинтегрируем полученное выражение
Проинтегрируем полученное выражение 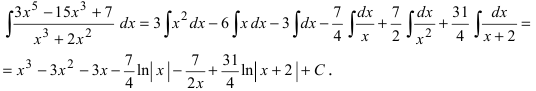 Интегрирование последней дроби рассмотрено ниже.
Интегрирование последней дроби рассмотрено ниже.
Интегрирование простых дробей
При интегрировании рациональных дробей возникают интегралы вида 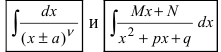 с квадратичным полиномом, имеющим отрицательный дискриминант
с квадратичным полиномом, имеющим отрицательный дискриминант 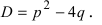
Интегралы первого вида 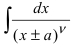 путем замены
путем замены 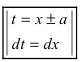 сводятся к табличным интегралам
сводятся к табличным интегралам 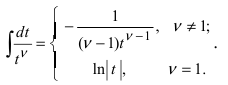 Интегралы второго вида
Интегралы второго вида 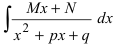 вычисляются с помощью замены
вычисляются с помощью замены 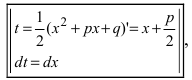 которая приводит к интегралу
которая приводит к интегралу 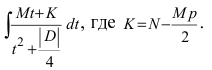
Использование метода тождественных преобразований подынтегральной функции позволяет записать этот интеграл в виде:
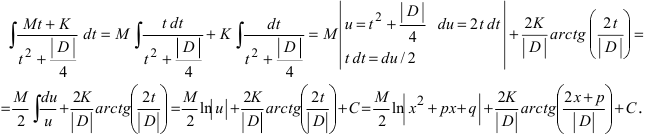
Пример:
Вычислить 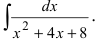
Решение:
Воспользуемся указанной выше заменой 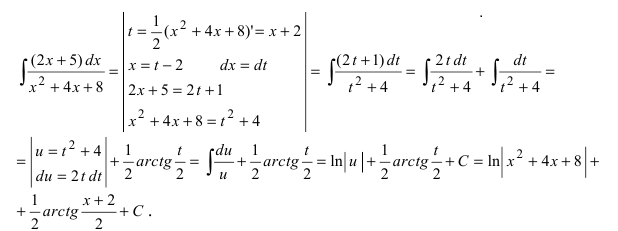
Интегрирование рациональных дробей
Определение 1. Рациональной дробью называется произвольная функция вида:
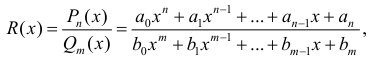
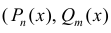 - многочлены степени n и m). Дробь R (x) - правильная, если n
- многочлены степени n и m). Дробь R (x) - правильная, если n
Элементарными рациональными дробями называются дроби вида:
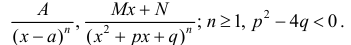
Интегрирование элементарных дробей.
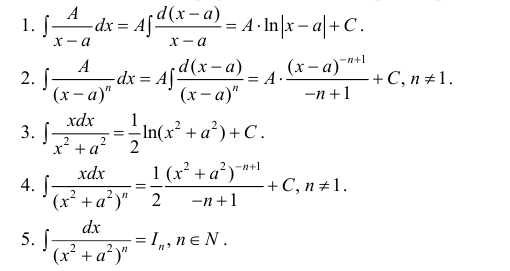
Найдем рекуррентную формулу для вычисления 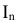 .
.
Пусть 1 > n.
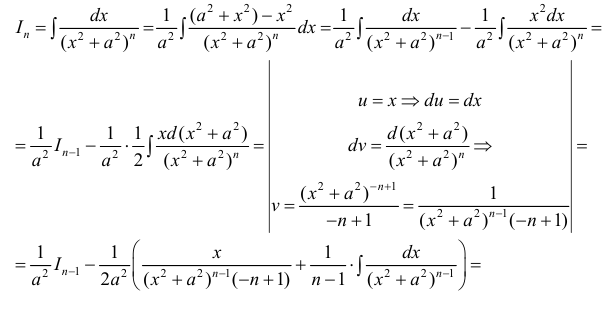
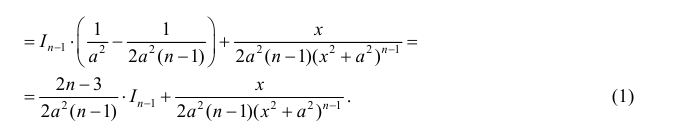
Вычисление интегралов
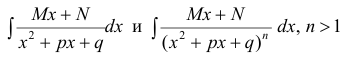
сведется к случаям 3 – 5, если выделить полный квадрат в трехчлене 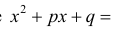
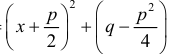 и сделать подстановку
и сделать подстановку 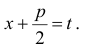
Пример 1.
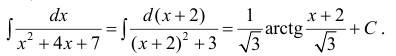
Пример 2.
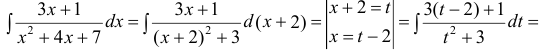
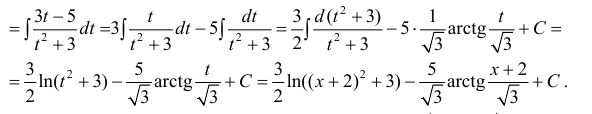
Пример 3.
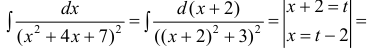
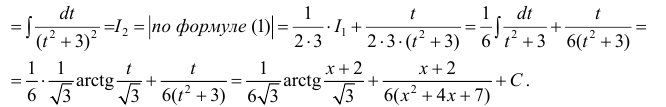
Теорема 1. Рассмотрим правильную рациональную дробь:
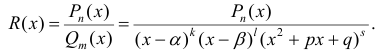
Дробь R (x) можно единственным образом разложить в сумму элементарных дробей:
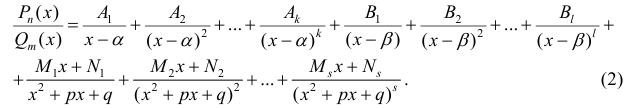
Коэффициенты 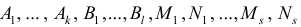 находятся, если правую часть равенства (2) привести к общему знаменателю и приравнять числители правой и левой части. Если дробь
находятся, если правую часть равенства (2) привести к общему знаменателю и приравнять числители правой и левой части. Если дробь 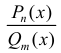 - неправильная, то делят
- неправильная, то делят 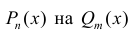 уголком и представляют дробь в виде:
уголком и представляют дробь в виде: 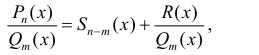 (3)
(3)
где 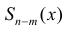 - частное, R(x) - остаток.
- частное, R(x) - остаток.
Пример 4.
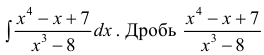 - неправильная. По формуле (3):
- неправильная. По формуле (3):
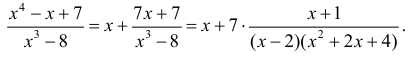
По формуле (2):
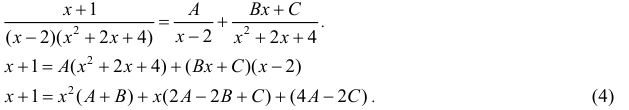
Для того, чтобы равенство (4) выполнялось ∀x∈R необходимо, чтобы равнялись друг другу коэффициенты при одинаковых степенях х.

Решив систему уравнений (5), получим:
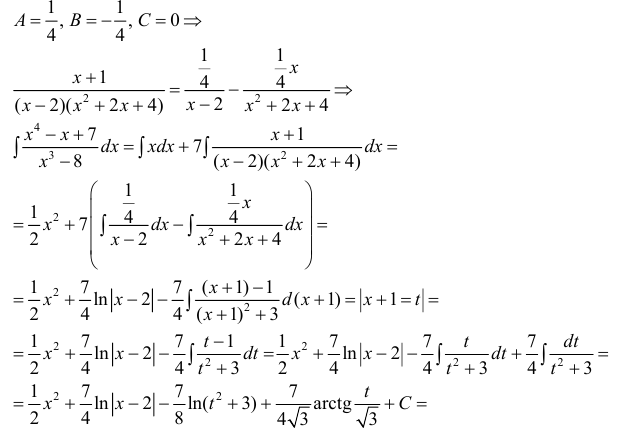
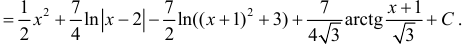
Если корни знаменателя 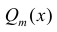 - действительны и имеют кратности 1, то коэффициенты в формуле (2) можно найти более простым способом.
- действительны и имеют кратности 1, то коэффициенты в формуле (2) можно найти более простым способом.
Пример 5.
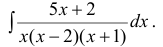
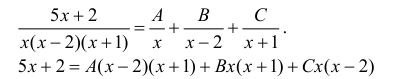
Подставляя в правую и левую части равенства конкретные значения x, получим:
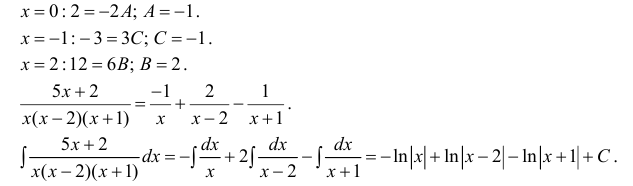
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Прямоугольная система координат на плоскости и ее применение
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение