
Инерциальные системы отсчета в физике - определение и формулы с примерами
Содержание:
Инерциальные системы отсчета:
Вы уже знаете, что движение и покой относительны. Если относительно одной системы тело находится в состоянии покоя, то относительно других систем отсчета тело может двигаться. Рассмотрим, например, шайбу, лежащую на ледовой площадке. Шайба находится в покое относительно льда (Земли), потому что влияние на нее Земли компенсируется влиянием льда. Но для хоккеиста, движущегося мимо шайбы прямолинейно и равномерно, она движется прямолинейно и равномерно в противоположную сторону. Таким образом, одно и то же тело (шайба) относительно одной системы отсчета (связанной с Землей) находится в покое, относительно другой (связанной с хоккеистом) движется прямолинейно и равномерно. Но хоккеист ударил по шайбе клюшкой (рис. 276).

В итоге очень непродолжительного действия клюшки шайба начинает двигаться, приобретая некоторую скорость. Интересно, что после удара, когда действие клюшки на шайбу уже прекратилось, шайба продолжает движение. Тем временем после удара влияние на шайбу других тел осталось таким же, как и до удара: как и раньше, действие Земли компенсируется действием льда, а клюшка, как и до удара, никакого влияния на движение шайбы не оказывает. Шайба после удара движется по прямой линии с почти постоянной скоростью, сообщенной ей в момент удара. Но шайба в конце концов остановится, хотя из опыта известно: чем более гладкими будут лед и шайба, тем более длительным будет движение шайбы. Поэтому можно догадаться, что если совсем устранить действие льда на подвижную шайбу (это действие называют трением), то шайба продолжала бы двигаться относительно Земли с постоянной скоростью без остановки.
Однако если бы рядом с этой шайбой, движущейся равномерно, двигался хоккеист с такой же скоростью, то относительно него (системы отсчета, связанной с ним) шайба находилась бы в покое. И в этом случае одно и то же тело в одной системе отсчета (Земля) движется прямолинейно и равномерно, относительно другой (хоккеист) - находится в покое.
Этот пример и много других, подобных ему, является проявлением одного из основных законов механики, который называют первым законом движения, или первым законом Ньютона.
Инерциальные системы отсчета
Существуют такие инерциальные системы отсчета, относительно которых тело, движущееся поступательно, сохраняет свою скорость постоянной, если на него не действуют другие тела (или действие других тел уравновешено).
Само явление сохранения скорости движения тела (в частности, состояние покоя) при компенсации внешних действий на тело называют инерцией. Поэтому первый закон Ньютона часто называют законом инерции. Повседневное выражение «движение по инерции» и означает движение тела с постоянной скоростью, когда действие других тел уравновешено.
В первом законе Ньютона речь идет о равномерном прямолинейном движении. Движение мы можем рассматривать только в какой-либо системе отсчета. Возникают вопросы: в какой же системе отсчета выполняется первый закон? Можно ли считать, что он выполняется в любой системе отсчета? Закон инерции выполняется не во всех системах отсчета.
Первый закон Ньютона дает возможность определить, является ли система отсчета инерциальной. Для этого следует выбрать какое-либо тело, для которого действующие силы уравновешены, и проследить за тем, как оно движется относительно системы отсчета, которая интересует нас. Если движение равномерное и прямолинейное (в отдельном случае - покой), то система инерциальна; если движение неравномерно - система неинерциальна.
Возникает вопрос: существуют ли строго инерциальные системы? Ньютон, формулируя закон инерции и включая его в основные законы динамики, утверждал этим, что такие системы отсчета в природе существуют. В действительности, если в природе имеет место закон инерции, то должна существовать и такая система отсчета, где он выполняется абсолютно строго, то есть инерциальная система отсчета. А если существует хотя бы одна такая система, то из этого следует, что их есть бесчисленное количество, потому что всякая система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной, будет также инерциальной.
Чтобы выяснить связь между силой, действующей на тело, и ускорением движения тела, следует выполнить опыт. Для проведения опыта выбираем тело, действующее на все другие тела с одинаковой силой. Таким телом может быть растянутая или сжатая пружина, в которой действует сила упругости. От всех других сил сила упругости отличается определенной особенностью, она зависит только от того, насколько растянута или сжата пружина, но не зависит от того, к какому телу пружина прикреплена. Поэтому на любое тело, прикрепленное к пружине, растянутой на определенную длину, действует одна и та же сила - сила упругости пружины.
Поскольку сила одна и та же, то какая-то величина должна быть одинакова для всех тел, которые ускоряются этой силой. На опыте и выясним, что это за величина.
Опыт. К тележке, масса которой известна (т), прикрепим один конец пружины, а второй ее конец прикрепим к нити с грузом, переброшенной через блок (рис. 277, а). Вследствие притягивания к Земле груз движется вниз и растягивает пружину. Она, растянутая на определенную длину Д(, действует силой упругости на тележку и сообщает ему ускорение. Это ускорение можно измерить, например, оно равно а.
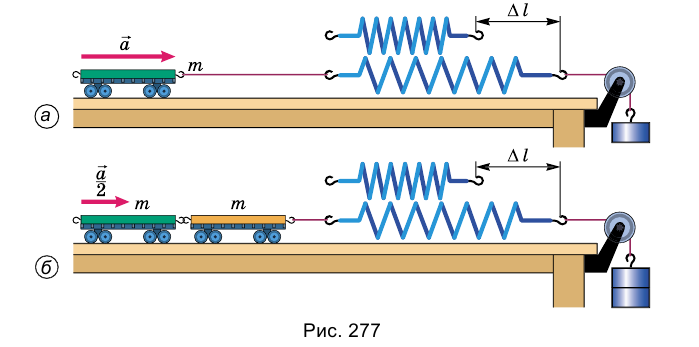
Повторим опыт с двумя тележками одинаковой массы (их масса - 2т), соединенными вместе (рис. 277, б). Нам необходимо измерить ускорение тележек при том же удлинении пружины, поскольку сила должна быть неизменной. Чтобы удлинение пружины было таким же, как в начале опыта, следует подвесить к нити другой груз. Опыт показывает, что при том же удлинении 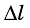 пружины ускорение двух тележек равно
пружины ускорение двух тележек равно 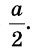 Если соединить три, четыре и больше тележек, то при том же удлинении
Если соединить три, четыре и больше тележек, то при том же удлинении 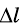 пружины ускорения тел окажется в три, четыре и больше раз меньше, чем одной тележки. Оказывается, что с увеличением массы тележки в определенное число раз ускорение, которое приобретает тело при действии той же силы, уменьшается во столько же раз. А это значит, что одинаковым оказывается произведение массы тележки и ее ускорения.
пружины ускорения тел окажется в три, четыре и больше раз меньше, чем одной тележки. Оказывается, что с увеличением массы тележки в определенное число раз ускорение, которое приобретает тело при действии той же силы, уменьшается во столько же раз. А это значит, что одинаковым оказывается произведение массы тележки и ее ускорения.
Это дало Ньютону основание утверждать, что сила определяется произведением массы тела и его ускорения, и сформулировать важнейший закон механики, который назвали вторым законом Ньютона.
Сила, действующая на тело, определяется произведением массы тела и его ускорения, предоставленного этой силой.
Формулу, выражающую второй закон Ньютона, следует записывать в таком виде: 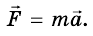 Из этой формулы можно получить выражение для
Из этой формулы можно получить выражение для
ускорения движения тела 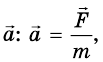 из которого видно, что ускорение тела
из которого видно, что ускорение тела
всегда направлено так же, как и сила, вызывающая его.
Ускорение движения тела прямо пропорционально силе, приложенной к нему, и обратно пропорционально массе тела и направлено в сторону действия силы.
Следует заметить, что второй закон Ньютона, как и первый, выполняется лишь для материальных точек. В случае действия сил на протяженное тело второй закон описывает ускорение не всего тела, а только его центра масс. При поступательном движении тела все его точки имеют одинаковые ускорения. Второй закон выполняется для всех точек.
Каждый из законов Ньютона постепенно раскрывает содержание одного из важнейших понятий механики - понятия силы. Если второй закон утверждает, что любая сила вызывает ускорение, то третий закон говорит, что все силы имеют характер взаимодействий.
Силы, с которыми какие-либо два тела действуют друг на друга, всегда равны по модулю и противоположны по направлению.
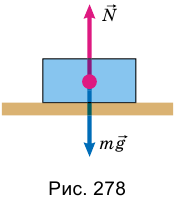
Пусть, например, на столе лежит тело (рис. 278).
С какой силой оно действует на стол 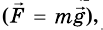 , с такой же по значению силой стол действует на тело N. Математически это записывают так:
, с такой же по значению силой стол действует на тело N. Математически это записывают так: 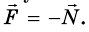 Знак «-» указывает на противоположность действия этих сил.
Знак «-» указывает на противоположность действия этих сил.
Третий закон Ньютона выполняется для подвижных тел
Однако равенство сил не всегда обусловлено третьим законом. Следует различать силы взаимодействия, приложенные к разным взаимодействующим телам, и так называемые равнодействующие силы, которые действуют на одно тело. Силы взаимодействия подчиняются третьему закону Ньютона, а силы, действующие на одно тело, подчиняются второму закону. Чтобы разобраться в этом подробнее, рассмотрим пример.
На поверхности Земли лежит тело (рис. 279). На тело действует сила 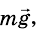 , с которой его притягивает Земля. Но по третьему закону Ньютона и тело притягивает к себе Землю с такой же по значению, но противоположно направленной силой
, с которой его притягивает Земля. Но по третьему закону Ньютона и тело притягивает к себе Землю с такой же по значению, но противоположно направленной силой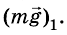 Следовательно,
Следовательно, 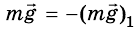 по третьему закону Ньютона.
по третьему закону Ньютона.
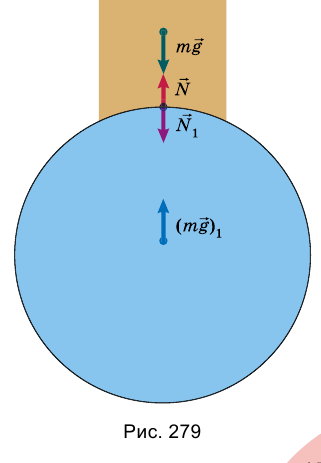
Кроме гравитационного взаимодействия Земли и тела, между ними существует еще и упругое: с какой силой тело действует на Землю, с такой же силой и Земля действует на тело, то есть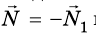 по третьему закону Ньютона.
по третьему закону Ньютона.
Таким образом, на тело действуют две силы: mg и N. Для этих сил, поскольку они приложены к одному телу, можно записать второй закон Ньютона:
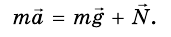
Тело находится в покое, то есть 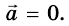 Поэтому
Поэтому 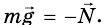 Это равенство сил доказано на основе второго закона Ньютона. На Землю также действуют две силы:
Это равенство сил доказано на основе второго закона Ньютона. На Землю также действуют две силы: 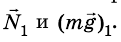 Они уравновешены, то есть
Они уравновешены, то есть 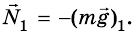 Это равенство так же является следствием применения второго закона.
Это равенство так же является следствием применения второго закона.
Пример задачи с решением
Велосипедист движется со скоростью 5 м/с. С какой скоростью двигался пешеход, вышедший из того же места на 1 час раньше, если велосипедист догнал его через 30 мин после начала своего движения?
Дано:
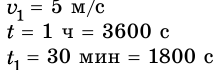
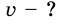
Решение:
Велосипедист и пешеход преодолели одинаковое расстояние, следовательно: 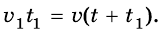
сюда: 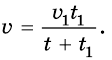
Подставим значение известных величин и по-
лучим: и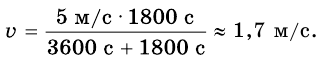
Ответ: 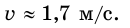
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |