Индуктивность и ее расчет

Содержание:

Индуктивность и ее расчет:

Основным соотношением для магнитного поля является принцип непрерывности магнитного потока: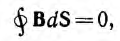

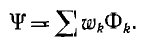
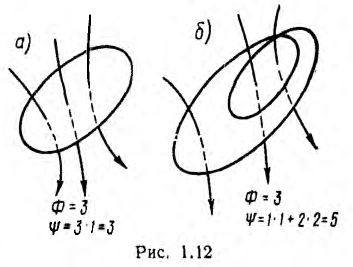
На рис. 1.12, а и б проиллюстрировано различие между потоком и
потокосцеплением, причем число линий в условном масштабе равно
величине потока.

Индукция измеряется в тесла (тл), магнитный поток и потокосцепление — в веберах (вб).
Индуктивность уединенного контура, равная отношению потокосцепления к току:

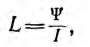
пропорциональна магнитной проницаемости среды, в которой он находится, и определяется конфигурацией контура. Единицей индуктивности является генри (гн).
Для расчета индуктивности контура необходимо предварительно рассчитать его магнитное поле по основному соотношению — закону полного тока:

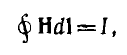
устанавливающему связь между напряженностью магнитного поля 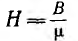и полным током I — алгебраической суммой токов, сцепляющихся с путем интегрирования. При этом положительное направление тока I связано с направлением dI обхода правилом правого винта.
Напряженность магнитного поля измеряется в а/м, магнитная проницаемость — в гн/м.
Если потокосцепление контура изменяется во времени, то в контуре появляется э. д. с. индукции е, величина и направление которой определяется законом электромагнитной индукции:

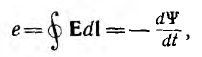
где Е — вектор напряженности наведенного в контуре электрического поля.
Таким образом, закон электромагнитной индукции связывает между собой изменение магнитного поля с возникающим электрическим полем.
Максвеллом было постулировано обобщение этого закона, заключающееся в том, что электрическое поле возникает при изменении магнитного поля в любой среде, а не только в проводящем контуре.

Закон электромагнитной индукции, открытый Фарадеем в 1831 г., был дополнен Ленцем в 1832— 1834 гг. Им было установлено общее правило: з. д. с. индукции всегда стремится создать ток, направленный так, чтобы препятствовать изменению потока, сцепляющегося с контуром.
При изменении тока в контуре изменяется потокосцепление ψ_L созданное этим током, и в контуре наводится э. д. с. самоиндукции

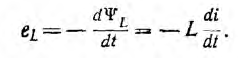
Индуктивность тороида и соленоида

Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ₀, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.

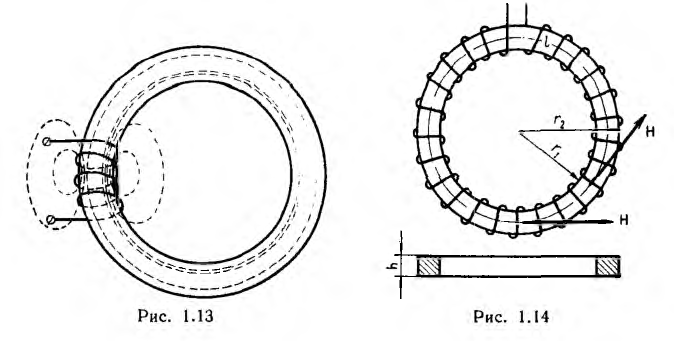
Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.

Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г₁ и г₂, магнитная проницаемость материала µ.

По закону полного тока для окружности с радиусом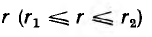

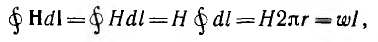
откуда

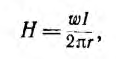
т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции

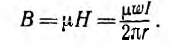
Поток в сердечнике тороида

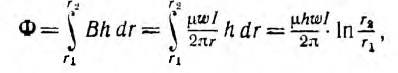
а потокосцепление

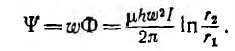
Отсюда индуктивность тороида

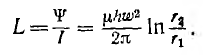
Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность

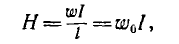
где w₀ — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,

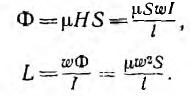
Обычно в реальных тороидах отношение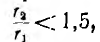 что приводит при этих приближенных формулах к погрешности, не превышающей 1,2 %. Последняя формула для индуктивности может быть применена и к длинному соленоиду, рассматриваемому как часть тороида бесконечно большого радиуса. Для соленоида конечной длины µ=µ₀

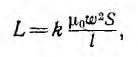
где k < 1 — коэффициент, учитывающий, что в таком соленоиде не весь поток пронизывает все витки.

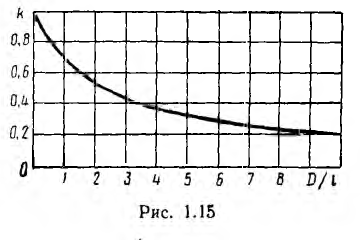
Как показывает точный расчет, этот коэффициент зависит от отношения диаметра D катушки к ее длине I (рис. 1.15). При 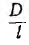= 0,1 коэффициент k — 0,96, поэтому при 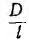< 0 ,1 приближенно принимают k = 1.

Индуктивность двухпроводной линии

Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г₀, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ₀. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.

Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса 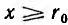дает:

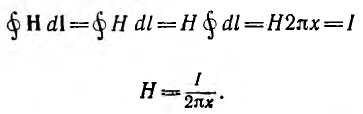
При интегрировании по окружности, лежащей внутри отдельного провода 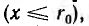охватывается лишь часть L_Х всего тока, протекающая внутри круга радиуса х, равная при равномерном распределении тока по сечению

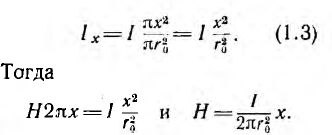
В воздухе между проводами на линии, соединяющей центры их сечений 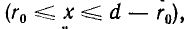направления полей, создаваемых обоими токами согласно правилу правого винта, совпадают и напряженности поля и индукции складываются:

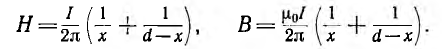
Эти же формулы справедливы и для 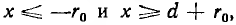т. е. снаружи линии, но здесь они дают разность полей.

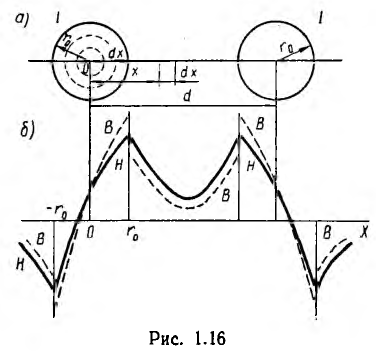
Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:

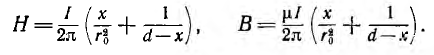
Внутри правого провода 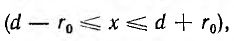соответственно,

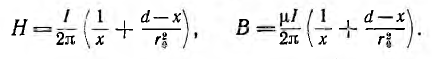
На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ₀. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.

На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,

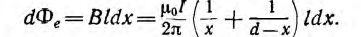
Весь поток между проводами - внешний поток

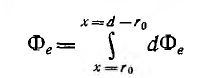
одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому

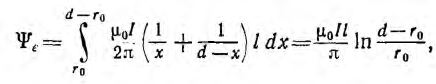
а соответствующая ему внешняя индуктивность

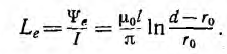
Для большинства линий расстояние d между проводами значительно превышает радиус r₀ проводов. В этом случае

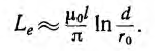
Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r₀ поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода

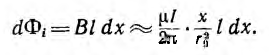
Так как поток dФ_i охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление

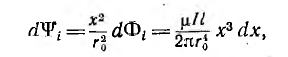
Весь поток между проводами — внешний поток

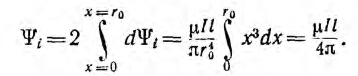
Соответственно, внутренняя индуктивность

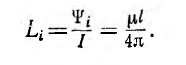
Суммарная индуктивность линии

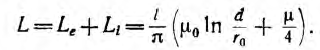
При медных или алюминиевых проводах (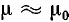) в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда

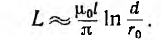
Для стальных проводов (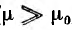) основной частью потока является
внутренний поток и индуктивность

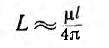
практически не будет зависеть от расстояния между проводами.

Взаимоиндуктивность и ее расчет

Для двух контуров, имеющих w₁ и w₂ витков с токами I₁ и I₂ (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф_1l—может быть разложен на поток рассеяния Ф_1s, пронизывающий только этот контур, и поток взаимоиндукции Ф_1m, пронизывающий также и второй контур:

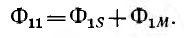
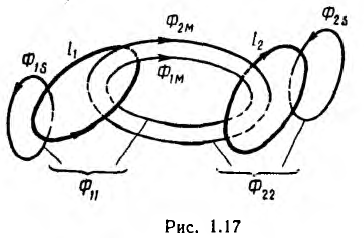
Потокосцепление, соответствующее потоку Ф₁₁ (при условии, что этот поток пронизывает все витки первого контура, равно

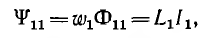
а потокосцепление рассеяния

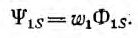
Аналогично для второго контура

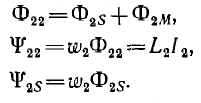
Потокосцепление второго контура, определяемое током первого,

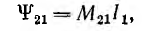
а потокосцепление первого контура, определяемое током второго,

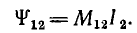
Можно показать, что

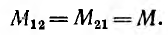
Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн).
Суммарный поток, пронизывающий первый контур,

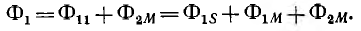
Суммарное потокосцепление первого контура

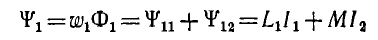
и соответственно для второго контура

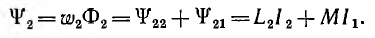
В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф_1м и Ф_2м (см. рис. 1.17).
Из изложенного видно, что

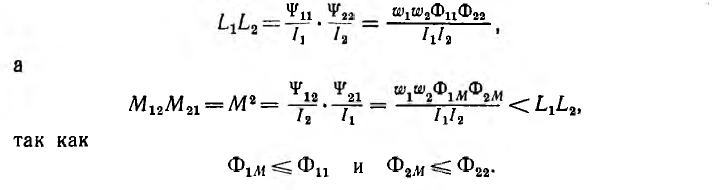
Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству

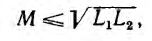
а используемый в технических расчетах коэффициент связи двух контуров

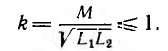
Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:

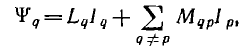
где L_q — индуктивность q-то контура, М_qp = М_рq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается
в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.

Взаимоиндуктивность двух параллельных двухпроводных линий

Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г₀ внутренним потоком в проводах по сравнению с внешним можно пренебречь.
Магнитный поток, пронизывающий первую линию и созданный током I₂ второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности.
Тогда магнитный поток, пронизывающий первую линию,

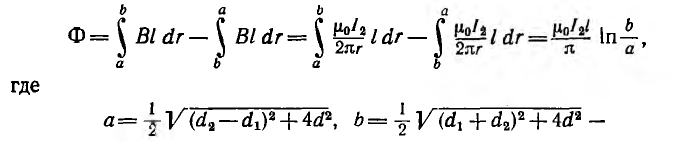
расстояния от провода линии 1 до проводов линии 2 .

Магнитный поток Ф одновременно является потокосцеплением 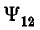первой линии, так как сцепляется с ней один раз; поэтому

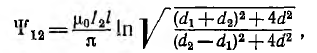
а взаимоиндуктивность

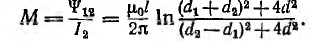
Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление 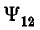будет равно нулю.

Линейные и нелинейные катушки индуктивности

У линейных материалов магнитная проницаемость µ, не зависит от напряженности поля и характеристика 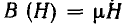для них изображается прямой линией (рис. 1.18, а). Магнитная проницаемость пропорциональна тангенсу угла а наклона этой прямой:

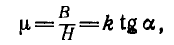
где k — масштабный коэффициент.

К нелинейным материалам относятся ферромагнетик и — железо, никель, кобальт и гадолиний. Важное значение в электротехнике имеют первые три элемента, главным образом в виде сплавов. У нелинейных материалов магнитная проницаемость очень велика 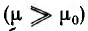и зависит от напряженности поля.

Подобно нелинейным диэлектрикам по кривой первоначальногo намагничивания В (Н) (рис. 1.18, б) могут быть определены статическая магнитная проницаемость

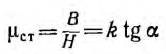
и дифференциальная, а при быстрых изменениях поля — динамическая магнитная проницаемость

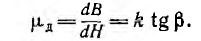
На рис. 1.18, б эти проницаемости представлены в функции напряженности поля. Максимальные значения магнитной проницаемости в очень чистом железе и в некоторых сплавах, например в пермаллое (сплав железа и-никеля с различными присадками), в сотни тысяч раз превышают магнитную постоянную равную

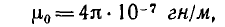
магнитной проницаемости вакуума.

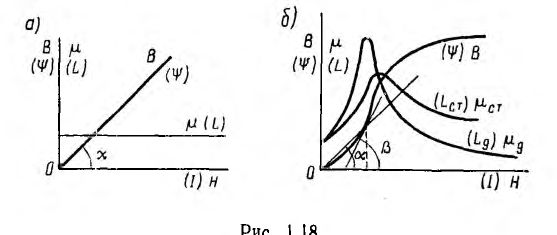
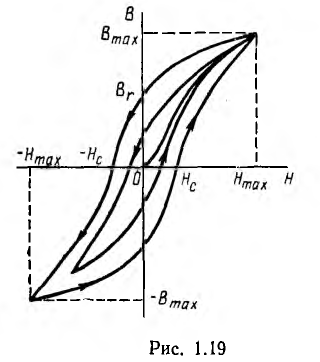
В переменных магнитных полях в ферромагнетиках имеет место явление магнитного гистерезиса (рис. 1.19), заключающееся в несовпадении кривой В (Н) при возрастании напряженности поля с кривой при убывании поля.

Кривая, соединяющая вершины петель гистерезиса, называется основной кривой намагничивания и практически совпадает с кривой первоначального намагничивания, Ферромагнитные свойства зависят от температуры и проявляются лишь в определенном ее интервале.

Для расчета индуктивности основной является зависимость потокосцепления ψ от тока I, называемая веберамперной характеристикой.

В зависимости от материала сердечника тороиды по виду своей веберамперной характеристики будут также линейными или нелинейными. В качестве примера рассматривается нелинейный тороид.

Для тороида 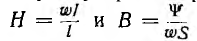и веберамперные характеристики ψ (I) в соответствующем масштабе совпадают с кривыми В (H); поэтому прямая и кривые на рис. 1.18 а и б соответствуют также веберамперным характеристикам при величинах, указанных в скобках.

Для нелинейных тороидов вводятся понятия статической индуктивности

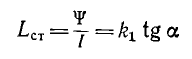
и дифференциальной, а также динамической индуктивности

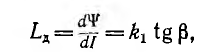
являющихся функциями тока (см. рис. 1.18, б); для линейных тороидов эти индуктивности совпадают.

Аналогично индуктивностям в нелинейных системах контуров вводятся статическая взаимоиндуктивность

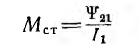
и дифференциальная, взаимоиндуктивность, а также динамическая

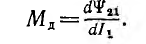
Индуктивность нелинейного тороида

Расчет нелинейного тороида может быть произведен, если задана зависимость В (H) или µ(H). Так как эти зависимости теоретически не выводятся, то для приближенного решения подбирают по кривой В(H) аппроксимирующую функцию.

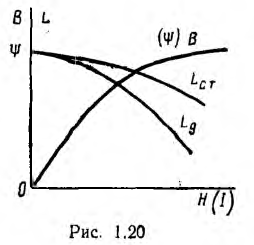
Пусть аппроксимирующая функция для характеристики В (H) (рис. 1.20)
материала сердечника тороида будет

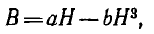
где а и b — постоянные.

Так как для тороида с ферромагнитным однородным cердечником напряженность поля по-прежнему определяется формулой 

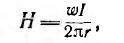
то индукция будет равна

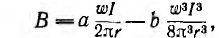
а потокосцепление

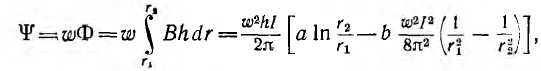
откуда статическая индуктивность

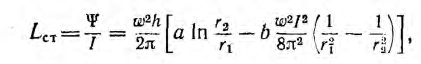
а дифференциальная индуктивность

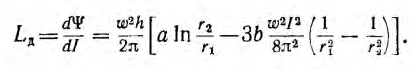
Кривые зависимости этих индуктивностей от тока представлены
на рис. 1.20.