Индуктивно связанные электрические цепи

Содержание:

Индуктивно связанные электрические цепи:

При изменении магнитного поля, связанного с каким-либо витком, в последнем наводится э. д. с., которая в соответствии с законом электромагнитной индукции определяется скоростью изменения магнитного потока независимо от того, чем вызвано изменение потока. В катушке, состоящей из большого числа витков, наводится э. д. с., пропорциональная скорости изменения потокосцепления, т. е. скорости изменения суммы магнитных потоков, сцепленных с отдельными витками данной катушки. Если все витки катушки пронизываются одним и тем же магнитным потоком, то, как указывалось  потокосцепление равно произведению магнитного потока на число витков.

При рассмотрении цепей синусоидального тока до сих пор учитывалось явление самоиндукции, т. е. наведение э. д. с. в электрической цепи при изменении потокосцепления самоиндукции, обусловленного током в этой цепи. Отношение потокосцепления самоиндукции к току характеризовалось скалярной величиной — индуктивностью L.

Теперь нам предстоит заняться рассмотрением явления взаимной индукции, т. е. наведения э. д. с. в электрической цепи при изменении потокосцепления взаимной индукции, обусловленного током в другой электрической цепи. Цепи, в которых наводятся э. д. с. взаимной индукции, называются индуктивно связанными цепями.

Связь потокосцепления взаимной индукции одной электрической цепи с током в другой цепи, равная отношению потокосцепления взаимной индукции в одной цепи к току в другой цепи, характеризуется взаимной индуктивностью M которая, так же как и индуктивность, представляет собой скалярную величину.

Если потокосцепление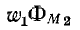

Справедливость последнего равенства можно доказать, если выразить потоки взаимной индукции 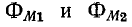через соответствующие м. д. с. 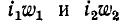и магнитную проводимость путей, по которым замыкаются эти потоки

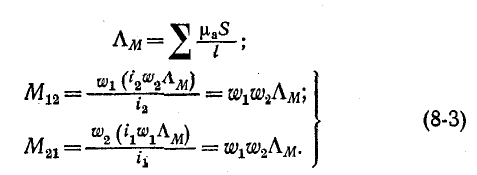
Отсюда также видно, что величина М пропорциональна произведению чисел витков катушек и магнитной проводимости пути общего потока, которая зависит от магнитной проницаемости среды и взаимного расположения катушек.

На основании сказанного формулируется свойство взаимности для индуктивно связанных цепей: если ток, проходящий в первой цепи, обусловливает во второй цепи потокосцепление взаимной индукции 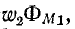то такой же ток, проходящий во второй цепи, обусловит в первой цепи потокосцепление взаимной индукции  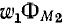  той же величины.

Полярности индуктивно связанных катушек эдс взаимной индукции

Напомним, что положительные направления тока и создаваемого им магнитного потока согласуются всякий раз по правилу правоходового винта. Условимся положительные направления токов 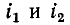в двух индуктивно связанных катушках считать согласными, если положительные направления создаваемых ими магнитных потоков самоиндукции и взаимной индукции совпадают.

На рис. 8-1, а и б показаны индуктивно связанные катушки, насаженные на общий магнитопровод; здесь в зависимости от направления намотки витков выбраны такие положительные направления для токов 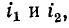при которых магнитные потоки самоиндукции и взаимной индукции в каждой катушке совпадают. Таким образом, рис. 8-1, а и б иллюстрирует согласное направление токов.

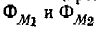Картина распределения мгновенных силовых трубок потоков не зависит от токов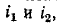т. е. при любых токах она одинакова; поэтому проводимость 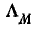для каждого из этих потоков одна и та же.

При согласном направлении токов 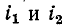в двух индуктивно связанных катушках выводы этих катушек, относительно которых токи 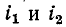направлены одинаково, называются одноименными или однополярными.

На рис. 8-1, а, где витки обеих катушек намотаны в одном направлении, одноименными выводами являются выводы, отмеченные точками (два других вывода на рис. 8-1, а составляют вторую пару одноименных выводов).

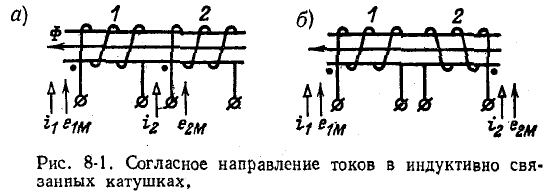
Аналогичным образом на рис. 8-1, б, где витки катушек намотаны в противоположных направлениях, одноименные выводы также отмечены точками.

Таким образом, одноименные выводы индуктивно связанных катушек характерны тем, что при одинаковом направлении токов 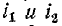относительно этих выводов магнитные потоки самоиндукции и взаимной индукции в каждой катушке складываются.

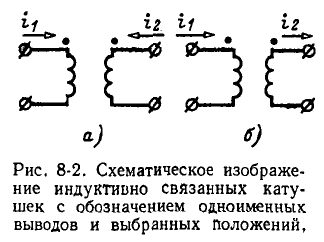
В связи с введением понятия об одноименных выводах при вычерчивании электрических схем нет необходимости показывать намотку витков индуктивно связанных катушек, а достаточно разметить на схеме их одноименные выводы. На рис. 8-2 показано схематическое изображение двух индуктивно связанных катушек с указанием одноименных выводов и выбранных положительных направлений токов 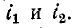Как это следует из сказанного выше, токи 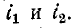направлены согласно на рис. 8-2, а и встречно на рис': 8-2, б.

Отмечалось, что положительное направление э. д. с. самоиндукции выбирается совпадающим с положительным направлением тока; поэтому положительные

направления магнитного потока и наводимой им э. д. с. самоиндукции связаны правилом правоходового винта. Точно так же и положительное направление э. д. с. взаимной индукции 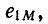наводимой в катушке 1 током 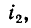принимается совпадающим с положительным направлением тока 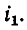Соответственно положительное направление э. д. с. взаимной индукции 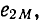наводимой в катушке 2 током 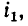совпадает с положительным направлением 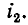При таких условиях и согласном направлении токов 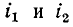в формуле э. д. с. взаимной индукции имеется знак «минус», так же как в формуле э. д. с. самоиндукции (1-2), причем положительное направление магнитного потока и наводимой э. д. с. взаимной индукции связано правилом правоходового винта:

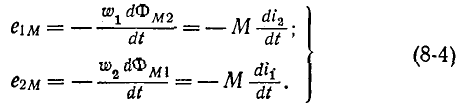
Рассмотрим случай, когда через катушку 1 проходит ток 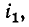причем 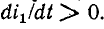На основании (8-4) в катушке 2
наводится э. д. с. взаимной индукции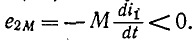

В этом случае потенциал вывода катушки 2, одноименный с тем, в который входит ток 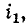оказывается выше потенциала второго вывода катушки 2.

Отсюда можно заключить, что одноименные выводы двух индуктивно связанных катушек обладают той особенностью, что подведение к одной из них возрастающего тока вызывает повышение потенциала на одноименном выводе второй катушки.

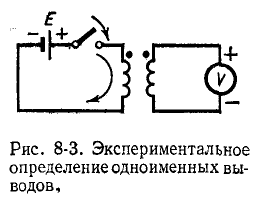
На указанном свойстве основано экспериментальное нахождение одноименных выводов индуктивно связанных катушек. Одна из них включается в цепь источника постоянного напряжения, а к другой присоединяется вольтметр постоянного тока (рис. 8-3).

Если в момент замыкания цепи источника стрелка измерительного прибора отклоняется в сторону положительных показаний, то выводы индуктивно связанных катушек, подключенные к положительному полюсу источника электрической энергии и положительному выводу измерительного прибора, являются одноименными.

Теперь рассмотрим случай встречного направления токов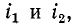 схематически изображенный на рис. 8-2, б, где токи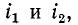направлены различно относительно одноименных выводов.

Ввиду того что положительные направления магнитных потоков самоиндукции и взаимной индукции в этом случае противоположны, э. д. с. взаимной индукции при встречном направлении токов вычисляются по формулам, содержащим знак плюс:

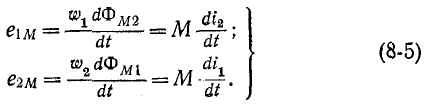
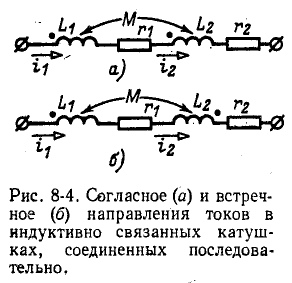
Рассмотрим последовательное соединение двух индуктивно связанных катушек (рис. 8-4, а и б).

При согласном направлении токов (рис. 8-4, а) э. д. с.

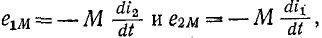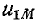
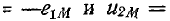
взаимной индукции совпадающие по направлению с токами, могут быть при обходе контура в том же направлении заменены падениями напряжения от взаимной индукции  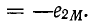Поэтому суммарное напряжение на обеих катушках с учетом того, что 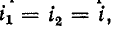равно:

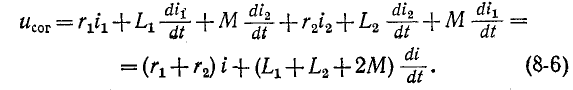
Полученное выражение показывает, что две индуктивно связанные катушки, соединенные последовательно, при согласном направлении токов эквивалентны катушке, имеющей активное сопротивление и индуктивность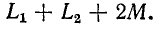

Таким образом, как и следовало ожидать, наличие взаимной индукции при согласном направлении токов в катушках, соединенных последовательно, увеличивает индуктивность цепи.

При встречном направлении токов (рис. 8-4, б) падение напряжения от взаимной индукции при обходе контура в направлении тока получается со знаком минус:

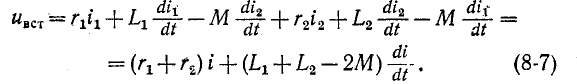
Данное выражение показывает, что две индуктивно связанные катушки, соединенные последовательно, при

встречном направлении" токов эквивалентны катушке, имеющей активное сопротивление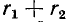 и индуктивность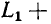

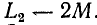
Следовательно, наличие взаимной индукции при ест речном направлении токов в катушках, соединенных последовательно, уменьшает индуктивность цепи.

На основании сказанного можно сделать следующий вывод: при согласном направлении токов падение напряжения от взаимной индукции имеет знак плюс, а при встречном — знак минус (обход цепи в обоих случаях совершается в положительном направлении тока).

Комплексная форма расчета цепи с взаимной индукцией

Представив ток в комплексной форме, получим выражение э. д. с. взаимной индукции для случая согласного направления токов в комплексной форме:

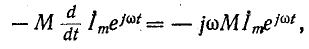
откуда комплексная действующая э. д. с. взаимной индукции

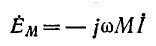
и соответственно падение напряжения от взаимной индукции

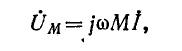
где 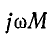— комплексное сопротивление взаимной индукции; в радиотехнике его называют сопротивлением связи.

Комплексные напряжения, соответствующие (8-6) и (8-7), запишутся так:

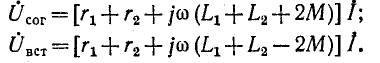
Отсюда, между прочим, вытекает следующий способ нахождения взаимной индуктивности М: если через 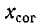обозначить индуктивное сопротивление цепи при согласном направлении токов последовательно соединенных элементов, а через 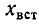— то же при встречном направлении, т. е. положить

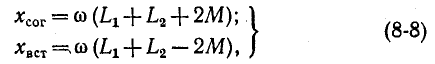
то в результате вычитания второго равенства из первого получим:

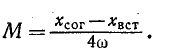
На рис. 8-5 изображены векторные диаграммы для случаев согласного и встречного направлений токов двух индуктивно связанных катушек, соединенных последовательно. При построении векторных диаграмм принято, что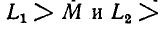 При этом как при согласном, так и при встречном направлениях токов ток 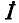отстает по фазе-от результирующего напряжения О. Если принять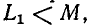то. и в этом случае ток получится отстающим, так как всегда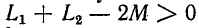. Условия 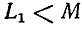и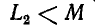 одновременно существовать не могут.

Порядок расчета разветвленных электрических цепей при наличии взаимной индуктивности иллюстрирован ниже на примере схемы рис. 8-6. Предполагается, что элементы 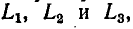входящие в схему, связаны индуктивно.

Заданными являются э. д. с. 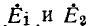и все параметры цепи. Искомыми являются токи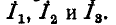

Если бы в каждом контуре был только один индуктивно связанный элемент, то запись уравнений для контурных токов не вызывала бы затруднений. В данном же случае

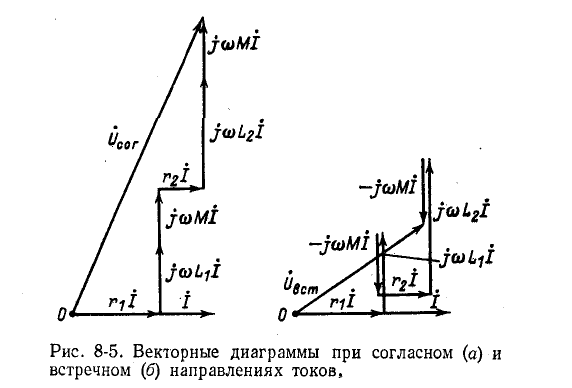
удобнее писать уравнения непосредственно для токов в ветвях, по первому и второму законам Кирхгофа. Совершая обход контуров по направлению токов 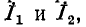, будем составлять уравнения напряжений по второму закону Кирхгофа с учетом падений напряжения в сопротивлениях взаимной индукции.

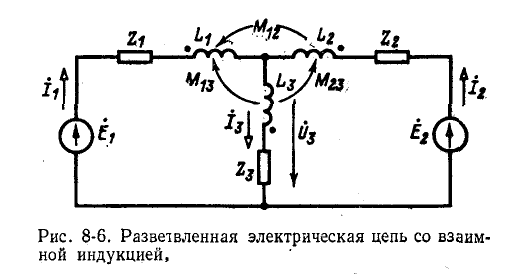
При согласном направлении токов падение напряжения в сопротивлении взаимной индукции входит со знаком плюс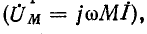 а при встречном —со знаком минус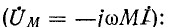

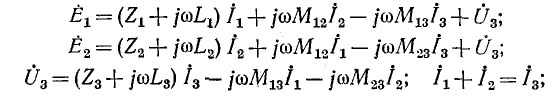
здесь 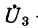— напряжение между узлами схемы. Решение уравнений дает токи.

Отметим, что слагаемые с одинаковыми взаимными индуктивностями входят в уравнения с одинаковыми знаками, что может служить проверкой правильности записи уравнений.

Таким образом, расчет разветвленной электрической цепи при наличии взаимной индуктивности может быть приведен одним из описанных ранее методов с учетом падений .напряжений в сопротивлениях взаимной индукции.

Метод узловых напряжений в данном случае непосредственно неприменим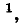так как токи в ветвях зависят не только от напряжений между узлами, к которым присоединены эти ветви, но и от токов других ветвей, с которыми они связаны через взаимную индукцию.

В разобранном выше примере одноименные выводы всех трех индуктивно связанных элементов были обозначены одинаково (звездочкой), так как предполагалось, что эти элементы имеют общий неразветвленный магнитопровод.

В том случае, когда три или большее число элементов располагаются на сложном, разветвленном магнитопроводе, необходимо одноименные выводы каждой пары индуктивно связанных элементов обозначать разными условными знаками (см. пример 8-2).

Пример 8-1.

Определить комплексное сопротивление на входе электрической цепи, состоящей из двух параллельно соединенных катушек, связанных индуктивно при согласном направлении токов (рис. 8-7).

Для положительных направлений контурных токов, показанных на рис. 8-7, составляем контурные уравнения:

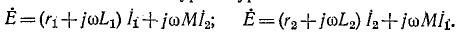
Обозначим:

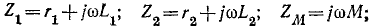
тогда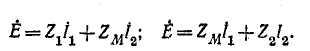

Решив уравнения относительно 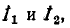найдем общий ток:
Искомое сопротивление всей цепи по отношению к выводам источника

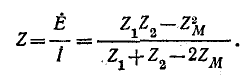
При переключении концов одной из катушек получается параллельное соединение катушек со встречным направлением токов. В этом случае в уравнениях и конечном выражении для Z следует принять 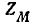со знаком минус, что приведет к изменению знака при 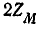в знаменателе упомянутого выражения,

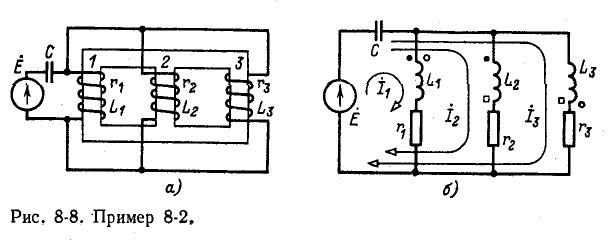
При отсутствии индуктивной связи 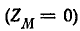конечное выражение совпадает с известной формулой для сопротивления двух параллельных ветвей.

Пример 8-2.

Составить уравнения контурных токов для электрической цепи, состоящей из источника э. д. с. Ё, емкости С и трех индуктивно связанных катушек, насаженных на трехстержневой магнито-провод (рис. 8-8, а). Взаимная индуктивность катушек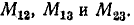 Цепь рассматривается как линейная (М — const).

Рисунок 8-8, 6 изображает электрическую схему заданной цепи. Точками, кружками и квадратиками обозначены одноименные выводы, соответствующие каждой паре катушек.

Выбрав направления контурных токов, указанные на схеме рис, 8-8, б, составляем контурные уравнения:

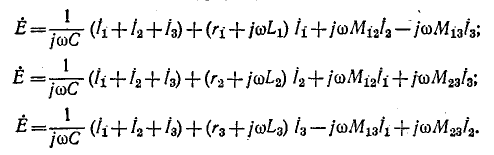
Совместное решение уравнений дает токи.

Предлагается читателям приведенную выше систему контурных уравнений получить матричным методом. Указание, Матрица соединений для схемы рис, 8-8 имеет вид:

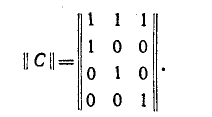
Матрица сопротивлений ветвей равна:

 

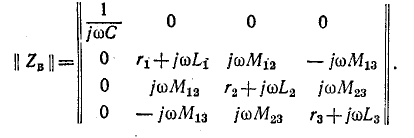
Коэффициент индуктивной связи. Индуктивность рассеяния

Рассмотрим картину магнитного поля индуктивно связанных катушек, схематически представленную на рис. 8-9 (для согласного направления токов).

Положим, что первая катушка состоит из витков, а вторая из 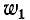витков, расположенных в каждой катушке настолько близко друг к другу, что магнитный поток охватывает целиком витки данной катушки.

В общем случае, когда по обеим катушкам проходят токи 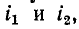магнитные потоки могут быть представлены как результат наложения потоков, создаваемых каждым током в отдельности.

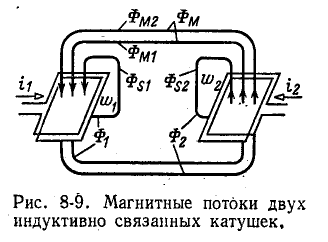
На рис. 8-9 приняты следующие обозначения магнитных потоков:

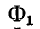— весь поток, созданный током 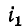первой катушки;

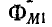- поток взаимной индукции первой катушки, пронизывающий витки второй катушки;

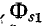— поток рассеяния первой катушки, пронизывающий только витки этой катушки;

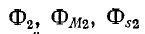— аналогичные потоки, созданные током 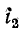второй катушки;

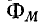— общий поток взаимной индукции, пронизывающий витки обеих катушек.

Из сказанного следует, что

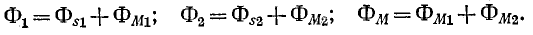
Чем меньше потоки рассеяния 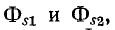тем больше приближается 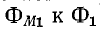и соответственно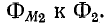

При изменении токов 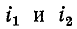во времени изменяются также и потоки, создаваемые этими токами. Индуктивность каждой катушки, как известно, определяется отношением потокосцепления самоиндукции к току данной катушки;

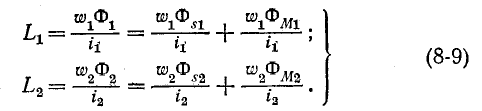
Первые слагаемые этих выражений:

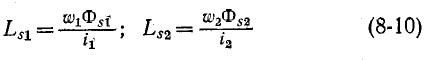
называются индуктивностями рассеяния катушек.

Магнитные потоки могут быть выражены через произведения м. д. с. на магнитные проводимости путей, по которым замыкаются эти потоки:

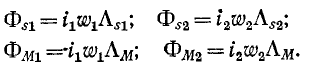
Следовательно,

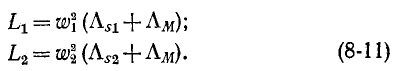
Таким образом, индуктивность катушки пропорциональна квадрату числа витков и сумме магнитных проводимостей путей потоков рассеяния и взаимной индукции.

Магнитная проводимость в свою очередь зависит от формы и размеров катушек, их взаимного расположения и магнитной проницаемости среды На основании (8-1), (8-2), (8-9) и (8-10) индуктивности рассеяния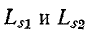 можно выразить через 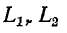и М следующими формулами:

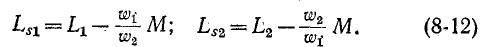
Эти выражения нам понадобятся в следующем параграфе при рассмотрении схемы замещения трансформатора.

Степень индуктивной связи двух катушек характеризуется коэффициентом связи k, определяемым как среднее геометрическое из отношений потока взаимной индукции ко всему потоку катушки, т. е.

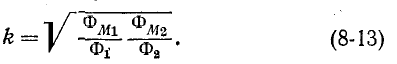
Если выразить потоки через параметры 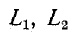и М по формулам (8-1), (8-2) и (8-9), то получим:

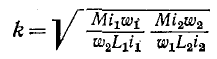
или

Из формулы (8-13) видно, что коэффициент связи всегда меньше единицы (так как 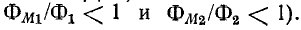Коэффициент связи возрастает с уменьшением потоков рассеяния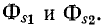

С учетом (8-3) и (8-11) коэффициент связи может быть выражен через магнитные проводимости:

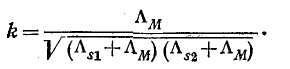
Повышение коэффициента связи достигается бифиляр-ным способом намотки катушек (рис. 8-10, а) и применением магнитопровода, так как с увеличением магнитной проницаемости и соответственно магнитной проводимости магнитопровода доля потоков рассеяния снижается.

При перпендикулярном расположении осей катушки (рис. 8-10, б) коэффициент связи обращается в нуль. Поэтому, перемещая одну катушку относительно другой, можно плавно изменять коэффициент связи в широких пределах, а при последовательном соединении этих катушек плавно изменять их результирующую индуктивность. Такое устройство называется вариометром.

При наличии магнитопровода цепь теряет свойство линейности. Однако в тех случаях, когда по условиям работы магнитная индукция в магнитопроводе не выходит за пределы прямолинейного участка кривой намагничивания и его магнитная проницаемость может быть принята постоянной, данная цепь рассматривается как линейная и изложенная выше теория сохраняет силу.

Как уже указывалось, схематическая картина магнитного поля на рис. 8-9 соответствует согласному направлению токов. Если изменить на рис. 8-9 положительное направление тока 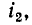то изменится направление магнитных потоков 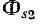и 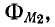что будет соответствовать встречному направлению токов.

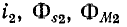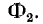В этом случае в уравнениях, приведенных" выше, должен быть изменен знак перед и При этом, как видно из предыдущих формул, величины 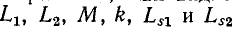сохраняются неизменными.

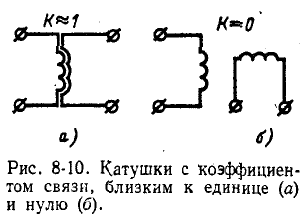
В предыдущем параграфе было показано, что при встречном направлении токов в двух катушках, соединенных последовательно, результирующая индуктивность равна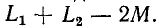

Докажем теперь, что величина 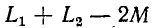всегда положительна. Для этого воспользуемся двумя неравенствами:

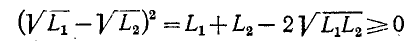
и

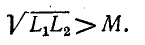
Заменив в первом неравенстве 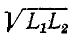меньшей величиной М, получим:

 

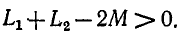
Пример 8-3.

Индуктивная катушка имеет w витков, соединенных последовательно-согласно. Индуктивность каждого витка равна L. Приняв коэффициент связи витков равным единице, определить результирующую индуктивность катушки.

При отсутствии рассеяния взаимная индуктивность каждой пары витков равна L, По аналогии с (8-6) результирующая индуктивность

катушки определится суммой индуктивностей всех витков и взаимной индуктивности, умноженной на число размещений из со витков по два:

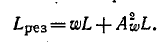
Так как

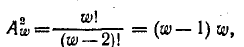
то

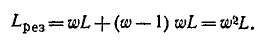
Как и следовало ожидать, на основании выражений (8-11) результирующая индуктивность катушки пропорциональна квадрату числа витков,
 

Уравнения и схемы замещения трансформатора без магнитопровода

Трансформатор представляет собой аппарат, передающий энергию из одной цепи в другую посредством электромагнитной индукции. Он применяется для различных целей, но чаще всего предназначается для преобразования переменных напряжений и токов х. Трансформатор состоит из двух или нескольких индуктивно .связанных обмоток, насаженных на общий магнито-провод.

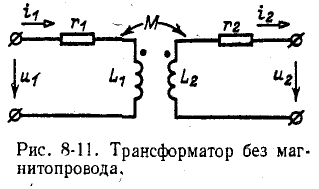
В настоящем параграфе рассматривается двухобмоточный трансформатор без Рис. 8-11. Трансформатор без маг-магнитопровода. Такой нитопровода, трансформатор может служить составной частью линейной электрической цепи в устройствах электроавтоматики, измерительной техники или связи.

Если пренебречь распределенными емкостями, существующими как между витками каждой из обмоток трансформатора, так и между самими обмотками и обмотками и землей, то трансформатор может быть представлен схемой рис. 8-11, в которой активные сопротивления обмоток условно вынесены и изображены отдельно.

¹ Отсюда происходит само название «трансформатор», т. е. преобразователь.

Обмотка трансформатора, присоединяемая к источнику питания, называется первичной, а обмотка, к которой  подключается нагрузка, — вторичной. Соответственно напряжения и токи на выводах этих обмоток называются первичными и вторичными. Следует заметить, что такие наименования в некоторых случаях являются условными, если в зависимости от режима энергия может передаваться, как в одну, так и в другую стороны..

При заданной полярности выводов обмоток трансформатора на схеме рис. 8-11 токи направлены встречно (что в данном случае не имеет принципиального значения).

Уравнения трансформатора в дифференциальной форме при встречном направлении токов имеют вид:

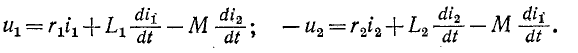
Если напряжения и токи синусоидальны, то уравнения трансформатора в комплексной форме запишутся следующим образом:
Эти уравнения равносильны следующим:

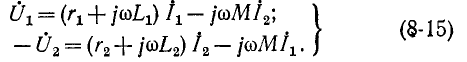
Эти уравнения равносильны следующим:

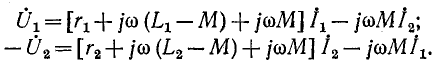
Последние уравнения являются контурными уравнениями, которые соответствуют схеме рис. 8-12.

Следовательно, эта схема может рассматриваться в качестве схемы замещения трансформатора без магнитопро-вода. В отличие от рис. 8-11 в схеме замещения первичная и вторичная цепи трансформатора связаны не индуктивно, а гальванически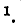

Если 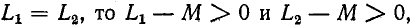так как коэффициент связи  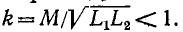При неравных знакоффициент связи  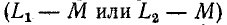может оказаться отрицательной. Например, если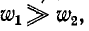то на основании (8-12)  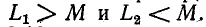   В этом случае

схема замещения рис. 8-12 может быть практически осуществлена только при фиксированной частоте, когда отрицательная индуктивность может быть замещена емкостным элементом; в общем же случае схема с линейным элементом, имеющим отрицательную индуктивность, практически нереализуема.

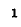Такая схема замещения дает возможность, например, применить метод узловых напряжений в цепи со взаимной индукцией.

Входящие в схему рис. 8-12 разности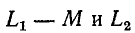 — М имеют физический смысл только при одинаковом числе витков первичной и вторичной обмоток 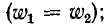в этом случае, как видно из (8-12), они представляют собой индуктивности рассеяния 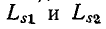первичной и вторичной обмоток трансформатора.

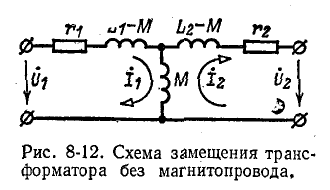
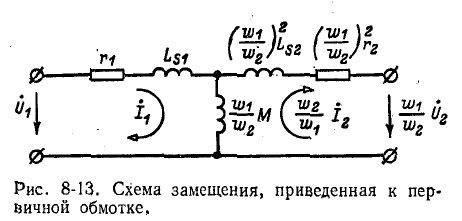
При неодинаковых числах витков первичной и вторичной обмоток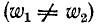на практике часто пользуются так называемой приведенной схемой замещения трансформатора, показанной на рис. 8-13. Приведение заключается в том, что напряжение 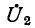и ток 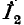заменяются величинами, приведенными к первичной обмотке:    напряжение 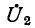умножается на n, а ток 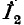делится на n. Здесь n = 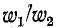— отношение чисел витков, которое называется коэффициентом трансформации.

Придав уравнениям (8-15) следующий вид:

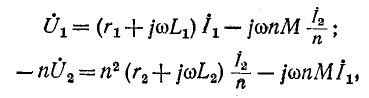
можно преобразовать их таким образом:

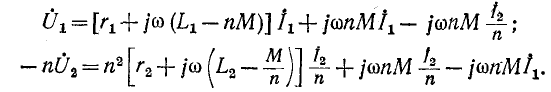
Полученные уравнения являются контурными уравнениями для приведенной схемы замещения трансформатора (рис. 8-13).

Схема замещения трансформатора, приведенная к первичной обмотке, содержит: сопротивление 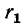и индуктивность рассеяния 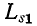первичной обмотки трансформатора;

индуктивность 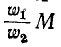в поперечной ветви (эта ветвь называется ветвью намагничивания); сопротивление 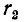и индуктивность рассеяния 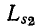вторичной обмотки, приведенные к первичной обмотке трансформатора, т. е. умноженные на 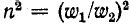(квадрат отношения чисел витков).

Индуктивные сопротивления 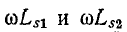представляют собой сопротивления рассеяния первичной и вторичной обмоток трансформатора, а индуктивное сопротивление 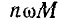— сопротивление ветви намагничивания. Магнитодвижущая сила, определяющая общий магнитный поток, который пронизывает первичную и вторичную обмотки,

при встречном направлении токов равна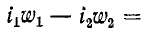 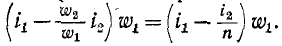Ток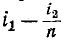и соответствующии ему комплексный ток /2—р-, который в схеме замещения трансформатора, приведенной к первичной обмотке, проходит через ветвь намагничивания, принято называть намагничивающим током трансформатора.

Схеме рис. 8-13 соответствует векторная диаграмма, показанная на рис. 8-14. При построении векторной диаграммы в качестве исходных могут быть приняты приведенные вторичные напряжение и ток.

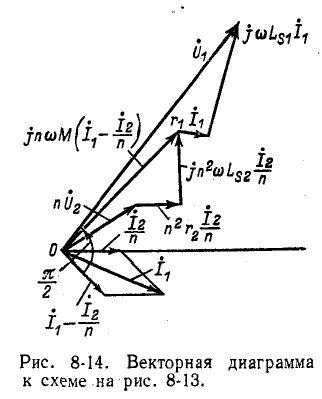
Падения напряжения от приведенного вторичного тока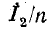в приведенных активном сопротивлении 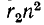и индуктивном сопротивлении рассеяния 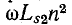вторичной обмотки геометрически складываются с приведенным вторичным напряжением 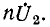Полученное напряжение равно падению напряжения от намагничивающего тока в индуктивном сопротивлении ветви намагничивания 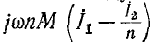причем намагничивающий ток отстает от полученного напряжения на 90°. Первичный ток находится как геометрическая сумма намагничивающего тока и приведенного вторичного тока:

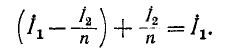
Падение напряжения от тока 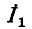в активном сопротивлении и индуктивном сопротивлении рассеяния первичной обмотки геометрически складывается с напряжением на ветви намагничивания, образуя первичное напряжение.

Ввиду того что вторичные электрические величины — напряжение 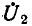и ток 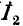— в схеме рис. 8-13 приведены к первичной обмотке, т. е. изменены пропорционально отношению числа витков, данная схема приведенного трансформатора не эквивалентна исходной схеме трансформатора. Для того чтобы схема замещения стала эквивалентной заданной схеме трансформатора, можно воспользоваться так называемым идеальным трансформатором, которому будем приписывать следующие свойства: при любых условия отношение первичного напряжения к вторичному на выводах идеального трансформатора равно отношению вторичного тока к первичному и определяется коэффициентом трансформации n. идеальный трансформатор не имеет потерь энергии и при разомкнутой вторичной обмотке через его первичную обмотку ток не проходит. В действительности такого трансформатора не существует, однако по своим свойствам к нему приближается трансформатор с коэффициентом связи, близким к единице, и столь большим числом витков, что сопротивление его ветви намагничивания 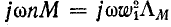практически равно бесконечности.

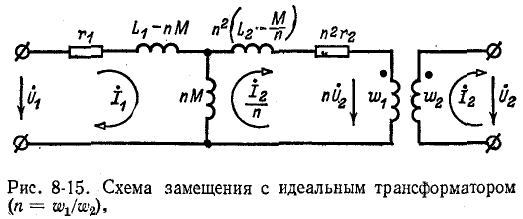
Дополнив схему рис. 8-13 идеальным трансформатором с коэффициентом трансформации n, получим эквивалентную схему трансформатора (рис. 8-15).

Рисунки 8-12—8-15 соответствуют встречному направлению токов, принятому в исходной схеме рис. 8-11.
Схема замещения с измененным положительным направлением вторичного тока соответствовала бы согласному направлению токов в исходной схеме.

Пример 8-4.

Решить пример 8-1 с помощью схемы замещения трансформатора (см. рис. 8-12).

Рассматривая индуктивно связанные элементы схемы рис. 8-16, а в качестве трансформатора с попарно соединенными первичными и вторичными выводами и пользуясь схемой замещения рис. 8-12 (с изменением направления тока 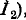, получаем эквивалентную схему рис, 8-16, б без индуктивных связей.

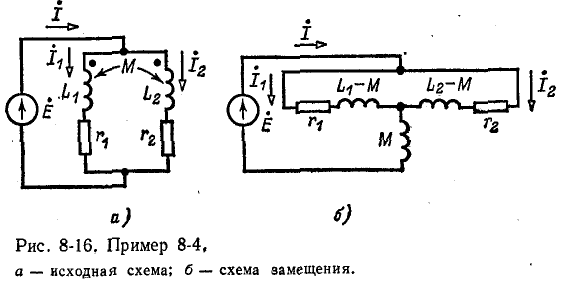
Комплексное сопротивление всей цепи равно:

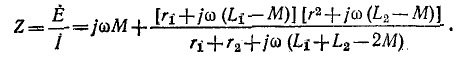
Применяя сокращенную запись

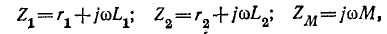
находим:

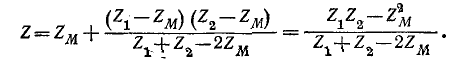
Энергия индуктивно связанных обмоток

Рассмотрим вопрос об энергии индуктивно связанных обмоток. Дифференциальные уравнения двух индуктивно связанных обмоток при встречном направлении токов (см, рис, 8-11) имеют вид:

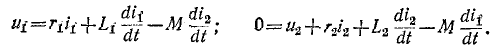
Умножив первое уравнение на 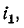а второе на 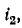сложив и сгруппировав Слагаемые, получим:

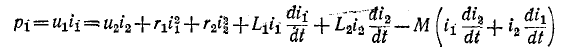
или

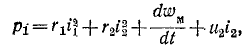
где 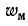— энергия магнитного поля:

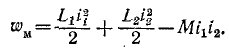
Как и следовало ожидать, мгновенная мощность,подводимая к трансформатору через первичные выводы, равна сумме мгновенных значений мощностей, расходуемых на нагрев обмоток, скорости изменения энергии 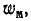накопленной в магнитном поле, и мощности, передаваемой нагрузке.

Первое слагаемое энергии магнитного поля равно энергии поля первой обмотки привторое слагаемое равно энергии поля второй обмотки при ; третье слагаемое представляет собой энергию, связанную с взаимным расположением обеих обмоток.

При согласном направлении токов третье слагаемое в выражении энергии будет иметь знак плюс.

Первое и второе слагаемые положительны, третье же в зависимости от знаков мгновенных токов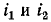 может иметь положительный или отрицательный знак. Поэтому энергия системы, состоящей из двух индуктивно связанных обмоток, может быть больше или меньше суммы энергий обеих обмоток, взятых отдельно.

Пример 8-5.

Две индуктивно связанные катушки имеют индуктивности 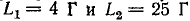; коэффициент связи k = 0,5.

Определить энергию поля, создаваемую этими катушками при токах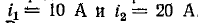

Взаимная индуктивность катушек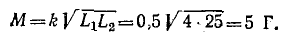

Энергия каждой катушки, взятой отдельно, составляет: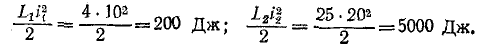

Энергия взаимного расположения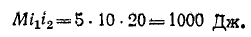

Энергия поля всей системы при согласном направлении токов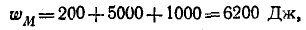

а при встречном направлении токов

 

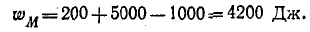
Входное сопротивление трансформатора

Если нагрузка 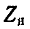присоединена к источнику электроэнергии не непосредственно, а через трансформатор (рис. 8-17), то согласно (8-15):

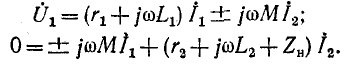
Следовательно, 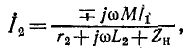откyда сопротивление на входных выводах трансформатора

 

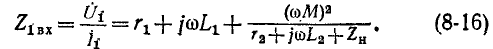
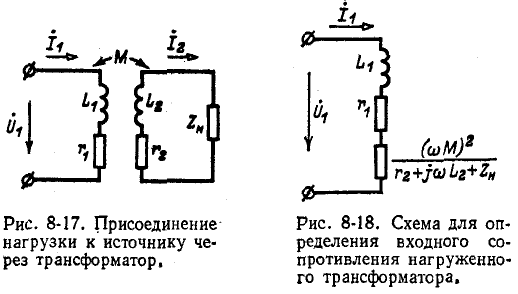
Третье слагаемое в правой части выражения (8-16) представляет собой комплексное сопротивление, вносимое из вторичной цепи в первичную; схема рис. 8-18 эквивалентна схеме рис. 8-17. В зависимости от характера 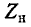мнимая часть вносимого сопротивления может быть положительной или отрицательной.

Допустим теперь, что нагрузка 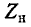присоединена к идеальному трансформатору. Учитывая условия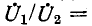 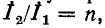которыми характеризуется идеальный трансформатор, получим входное сопротивление

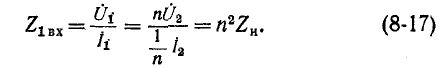
Следовательно, идеальный трансформатор, включенный между нагрузкой и источником электроэнергии, изменяет сопротивление нагрузки пропорционально квадрату коэффициента трансформации без изменения его угла.

Это свойство практически используется в различных областях электротехники, проводной связи, радио, приборостроения, автоматики для уравнивания сопротивлений источника и нагрузки (с целью повышения отдаваемой источником мощности).

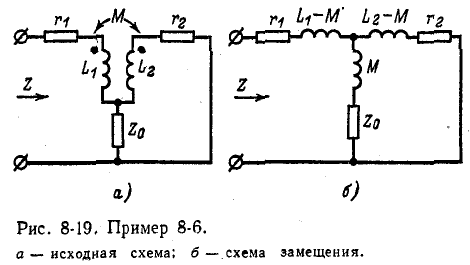
Поэтому в том случае, когда требуется изменить сопротивление какой-либо нагрузки без изменения самой нагрузки, включается промежуточный трансформатор, по свойствам приближающийся к идеальному трансформатору с коэффициентом трансформации, определяемым на основании (8-17):

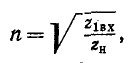
где 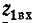— требуемое сопротивление.

Формула (8-17) непосредственно вытекает также из приведенной схемы замещения трансформатора (см. рис. 8-13), поскольку идеальный трансформатор не имеет активных сопротивлений и индуктивностей рассеяния 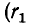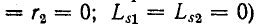и его взаимная индуктивность равна бесконечности.

Входное сопротивление идеального трансформатора при замкнутых выходных выводах равно нулю, а при разомкнутых — бесконечности.

Пример 8-6.

Определить входное сопротивление цепи, показанной на рис. 8-19, а.

Пользуясь схемой замещения, представленной на рис. 8-19, б, находим:

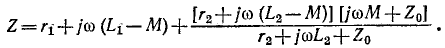
Пример 8-7.

Определить входное сопротивление цепи, состоящей из двух трансформаторов, включенных каскадно с нагрузкой 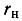на выходе (рис. 8-20, а). Активные сопротивления обмоток трансформаторов не учитываются.

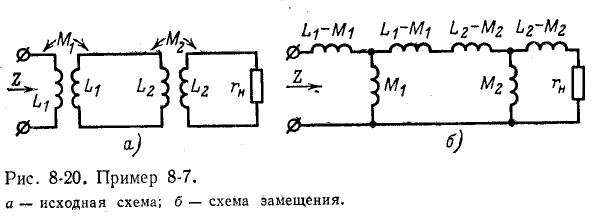
В соответствии с (8-16) входное сопротивление второго трансформатора будет:

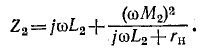
Рассматривая 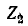в качестве нагрузки первого трансформатора, определяем входное сопротивление цепи по той -же формуле (8-16):

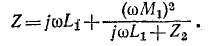
После преобразования находим:

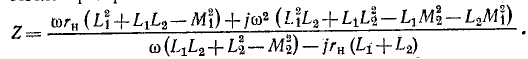
К тому же результату можно прийти на основе схемы замещения, показанной на рис. 8-20, б.
 

Автотрансформатор

Автотрансформатор отличается от трансформатора тем, что его обмотка низшего напряжения является частью обмотки высшего напряжения (рис. 8-21, а). Так же как и трансформатор, он может быть понижающим или повышающим.

Уравнения автотрансформатора в комплексной форме для указанных на рис. 8-21, а положительных направлений токов и напряжений записываются так:

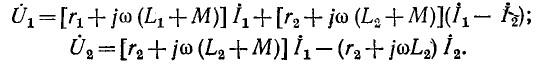
Эти уравнения соответствуют схеме замещения, показанной на рис. 8-21, б. Правая ветвь схемы состоит из практически неосуществимого линейного элемента — отрицательной индуктивности (—М). Поэтому полученная схема замещения рис. 8-21, б может быть использована только для расчета. Практически осуществить ее можно только для фиксированной частоты, когда элемент — М

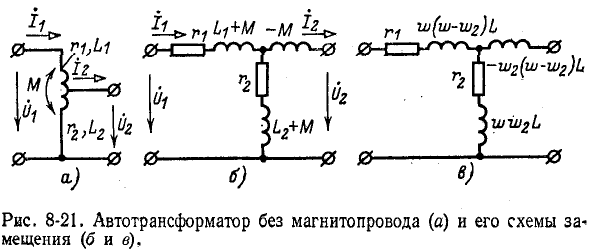
замещается емкостью. Однако если индуктивность нагрузки, подключенной к выходным выводам, компенсирует отрицательную индуктивность, то схема замещения автотрансформатора в сочетании с нагрузкой практически осуществима.

Итак, схема замещения автотрансформатора представляет собой трехлучевую звезду. Сопротивления лучей этой звезды могут быть найдены и другим способом, если поочередно приравнять суммы сопротивлений двух лучей сопротивлениям между соответствующими выводами автотрансформатора (при разомкнутом трётьем выводе).

Обозначим: индуктивность каждого витка L, общее число витков 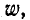, число витков обмотки низшего напряжения 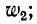приняв коэффициент связи равным единице, т. е. пренебрегая рассеянием, получим в этом случае схему замещения автотрансформатора, показанную на рис. 8-21, в.

В режиме холостого хода автотрансформатора (т. е. при разомкнутых выходных выводах), если не учитывать рассеяния, отношение первичного напряжения 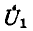к вторичному 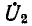равно отношению суммарного числа витков обмотки к числу витков обмотки низшего напряжения:

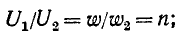
n — коэффициент трансформации автотрансформатора.

При нагрузке подводимая к автотрансформатору мощность передается на вторичную сторону как посредством электромагнитной индукции (через магнитное поле), так и непосредственно через электрическую связь.

Применение автотрансформатора вместо обычного трансформатора той же мощности и с таким же коэффициентом трансформации дает экономию в меди, затрачиваемой на обмотку. Экономия достигается за счет сокращения общего числа витков и уменьшения толщины провода обмотки, через которую проходит ток, равный разности первичного и вторичного токов.

Экономия в меди тем больше, чем ближе к единице коэффициент трансформации, так как при этом уменьшается разность токов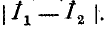

Индуктивно связанные колебательные контуры

В радиотехнике широко распространены двухконтурные колебательные системы, в которых связь между контурами осуществляется при помощи взаимной индукции.

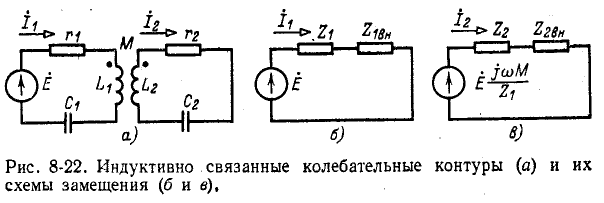
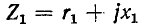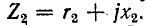На рис. 8-22, а показаны колебательные контуры с индуктивной (трансформаторной) связью. Обозначим собственные сопротивления контуров через  и На основании сопротивление, вносимое из вторичной цепи в первичную, равно:

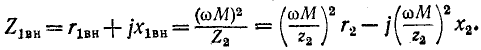
На рис. 8-22, б изображена схема замещения для первичного контура. Первичный ток равен:

а вторичный ток

Следует заметить, что напряжение 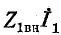на сопротивлении, вносимом из вторичного контура в первичный, равно —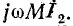

Подставив (8-18) в (8-19) и умножив числитель и знаменатель на 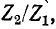 получим:

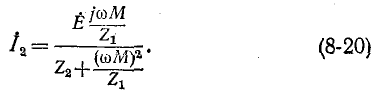
Выражение (8-20) могло быть выведено и по теореме об эквивалентном источнике.

Числитель полученной дроби равен э. д. с., наводимой во вторичном контуре, когда он разомкнут, а знаменатель представляет собой эквивалентное сопротивление вторичного контура, в котором влияние первичного контура учтено сопротивлением 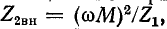вносимым из первичного контура во вторичный.

Схема замещения для вторичного контура показана на рис. 8-22, в; здесь

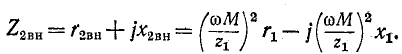
Активные составляющие вносимых сопротивлений всегда положительны, а знаки реактивных составляющих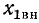 и 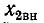противоположны знакам реактивных сопротивлений 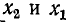соответственно.

Как 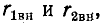так и 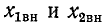зависят от частоты. По мере приближения частоты источника к резонансной частоте вторичного контура 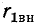возрастает, стремясь к максимальному значению 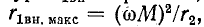 а 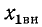стремится к нулю, В свою очередь если частота приближается к резонансной частоте первичного контура, то 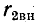растет, стремясь к 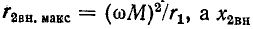стремится к нулю.

Настройка связанных контуров

На практике часто добиваются получения максимального тока 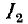(или максимальной мощности Р2) во вторичном контуре. Это достигается соответствующей настройкой связанных контуров. Существуют различные способы настройки, а именно:

1. изменением параметров первичного контура, например емкости 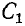, резонанс, который при этом возникает, называется первым частным резона н-с о м;
2. изменением параметров вторичного контура, например емкости 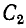; в этом случае возникает второй частный резонанс;
3. изменением параметров одного из контуров и сопротивления связи; резонанс в этом случае называется сложным;
4. изменением параметров обоих контуров и сопротивления связи; в этом случае резонанс называется полным.

Первый частный резонанс:

Согласно (8-19) вторичный ток прямо пропорционален первичному. Поэтому максимуму тока 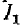соответствует и максимум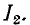

Первый частный резонанс наступает при

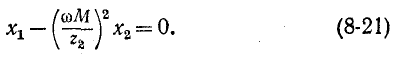
В этом случае: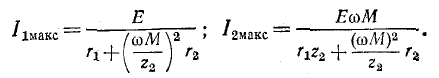
Второй частный резонанс наступает при

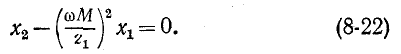
При этом

 

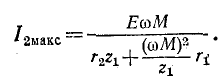
Сложный резонанс:

При настройке первичного контура оптимальное сопротивление связи найдем, приравняв нулю первую производную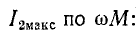

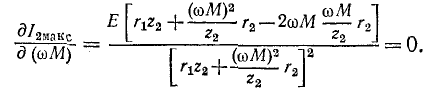
Отсюда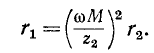

Следовательно, оптимальное сопротивление связи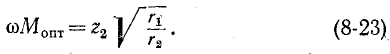

' В этом случае получается максимум максиморум вторичного тока:

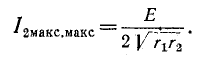
Условия (8-21) и (8-23), которые при этом выполняются, означают, что собственное сопротивление первичного контура равно сопротивлению, комплексно сопряженному с сопротивлением, вносимым из вторичного контура в первичный, т. е.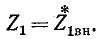
Из [формулы (3-17)] известно, что это и есть условие передачи максимума активной мощности от источника к приемнику.

Аналогично при настройке вторичного контура оптимальное сопротивление связи равно:

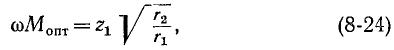
причем условия (8-22) и (8-24) в совокупности означают,
что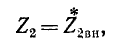
т. е. и в этом случае выполняется условие передачи максимума активной мощности от источника к приемнику. При этом

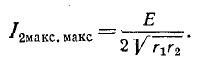
Следовательно, при сложном резонансе максимум максиморум вторичного тока не зависит от того, какой из контуров настраивается на резонанс.

Полный резонанс:

При настройке на полный резонанс сначала настраивают первичный контур при разомкнутом вторичном, т. е. добиваются условия 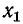= 0. Затем настраивают вторичный контур, добиваясь условия 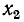= 0. Наконец, подбирают оптимальное сопротивление связи. При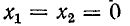

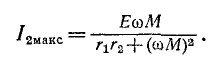
Оптимальное сопротивление связи находится из условия

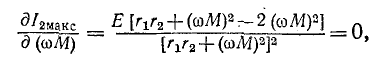
откуда

При этом вторичный ток равен:

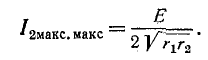
Хотя максимум максиморум вторичного тока при настройке на полный резонанс и получается таким же, как при настройке на сложный резонанс, настройка на полный резонанс имеет то преимущество, что сопротивление связи меньше, чем при сложном резонансе, оно как и активные сопротивления 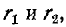исчисляется единицами ом.

Эффективность передачи энергии из первичного контура во вторичный оценивается коэффициентом полезного действия двухконтурной системы, равным отношению мощности, поглощаемой сопротивлением 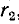, к сумме мощностей, поглощаемых сопротивлениями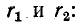

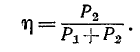
Очевидно, 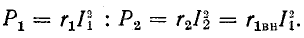Поэтому

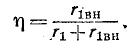
Когда вторичный контур настроен на частоту источника,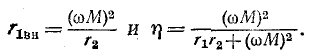

При настройке на полный резонанс 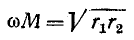и 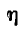= 0,5.

Если колебательные контуры идентичны и частота близка к резонансной, то оптимальный коэффициент связи при настройке на полный резонанс с учетом (8-25) примерно равен затуханию контура:

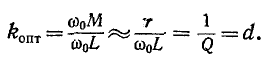
Например, для радиотехнических контуров с добротностью Q = 100 оптимальный коэффициент связи составит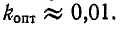
 

Резонансные кривые и полоса пропускания связанных контуров

Ограничимся рассмотрением случая, когда связанные колебательные контуры имеют одинаковые резонансную частоту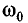 и добротность Q.

Для построения резонансных кривых вторичного тока воспользуемся выражением (8-20), приняв 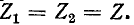При рассмотрении последовательного колебательного контура встречалось выражение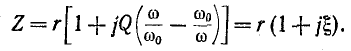
Величина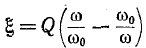называется обобщенной расстройкой контура.

При частотах, близких к резонансной, 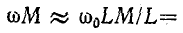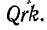Поэтому

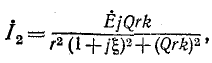
откуда

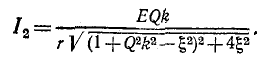
Отнеся вторичный ток к току 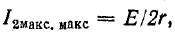получим:

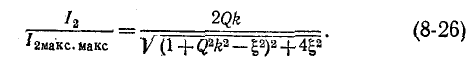
Если контуры настроены на частоту источника, то 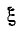= 0 и

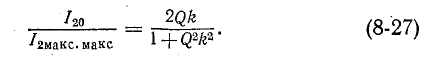
Выясним, каким значениям 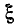соответствуют максимумы резонансной кривой 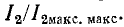Приравняв нулю производную по 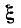от подкоренного выражения (8-26), получим три корня: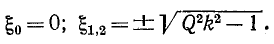

При Qk < 1 второй и третий корни лишены физического смысла и резонансная кривая имеет только один максимум — при 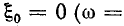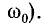Вторичный ток при ЭТОМ меньше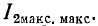

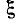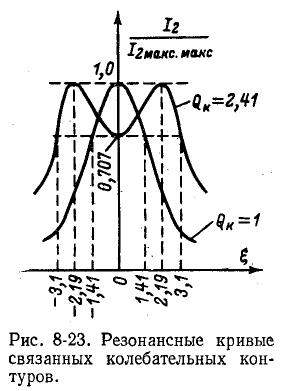
При Qk = 1 и = 0 получаем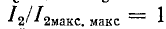 т.е. вторичный ток достигает значения максимума максиморум. При Qk > 1 резонансная кривая получается двугорбой, причем впадина двугорбой кривой соответствует значению 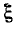= 0, а 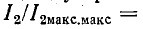. 1 соответствует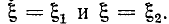

Сказанное иллюстрируется рис. 8-23.

Легко показать, что при 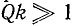, когда 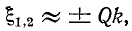максимумы вторичного тока соответствуют частотам

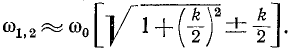
Коэффициент связи k = 1/Q = d, при котором получается предельная одногорбая резонансная кривая, называется критическим. Он совпадает с оптимальным коэффициентом связи двух идентичных контуров, настроенных на полный резонанс.

Полосой пропускания связанных колебательных контуров, как и в случае одиночного колебательного контура, условно считается область частот, на границах которой резонансная кривая снижается не более чем в 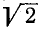раз по сравнению с максимумом.

Так как

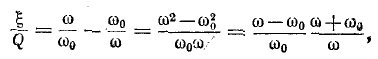
то приняв вблизи резонансной частоты
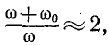можно считать, что 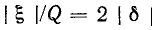определяет полосу пропускания связанных контуров при 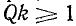(здесь 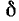— относительная расстройка частоты). Решением уравнения

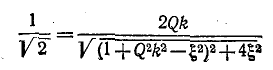
служит

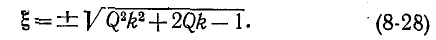
Это выражение справедливо до тех пор, пока впадина резонансной кривой находится выше или совпадает c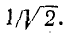 В предельном случае  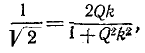  откуда Qk = 2,41.

Подставив это значение Qk в (8-28), найдем:

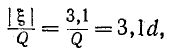
т. е. при Qk = 2,41 полоса пропускания в 3,1 раза больше, чем у одиночного колебательного контура.

Если Qk = 1, то 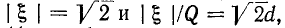, т. е. полоса пропускания в 1,41 раз больше, чем у одиночного контура.

При Qk = 0,68 полоса пропускания связанных контуров равна полосе пропускания одиночного контура, а при 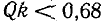она меньше полосы пропускания одиночного контура.

Величина Qk в радиотехнической литературе носит название параметра связи.
(8-28)