Идеализированные пассивные элементы

Содержание:

Идеализированные пассивные элементы:

Сопротивление

Используемые в теории цепей идеализированные двухполюсные элементы — сопротивление, емкость и индуктивность — являются пассивными, так как энергия, потребляемая ими от остальной части цепи в любой момент времени, положительна или равна нулю.

Сопротивление — идеализированный пассивный элемент, в котором электрическая энергия необратимо преобразуется в какой-либо другой вид энергии, например в тепловую, механическую или световую. Запасания энергии электрического или магнитного полей в сопротивлении не происходит. Термин «сопротивление» используют не только для обозначения идеализированного элемента, но и как количественную характеристику способности этого элемента преобразовывать электрическую энергию в другие виды энергии.

По свойствам к идеализированному пассивному элементу — сопротивлению наиболее близки высококачественные резисторы — реальные элементы электрической цепи, в которых электрическая энергия в основном преобразуется в тепловую. Важнейшей характеристикой резистора, которая определяет меру преобразования электрической энергии в тепловую, является его сопротивление. Помимо основного процесса —преобразования электрической энергии в тепловую - в резисторе имеют место также другие процессы, Например запасание энергии электрического и магнитного полей. Идеализированный элемент электрической цепи — сопротивление — можно рассматривать как упрощенную модель резистора, в которой абстрагируется только его основная характеристика — сопротивление.

Итак, термин «сопротивление» можно использовать трояким образом — как основную характеристику реального элемента электрической цепи — резистора, как название идеализированного элемента электрической цепи и как единственную характеристику этого элемента.(Использование термина «сопротивление», а также вводимых далее терминов «емкость» и «индуктивность», не только в качестве характеристик реального и идеализированного элементов, но и в качестве названий идеализированных элементов является не вполне удачным н оправдывается только компактностью изложения. Более точными, но в то же время более громоздкими были бы следующие названия соответствующих идеализированных элементов: «идеальный резистор", "идеальный конденсатор».

 Условное графическое обозначение сопротивления приведено на рис. 1.2. Условно-положительные направления напряжения и тока показаны стрелками. Рядом с условным графическим обозначением сопротивления ставят его условное буквенное обозначение

Вольт-амперная характеристика резистора, т. е. зависимость между значениями тока и напряжения на его зажимах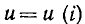

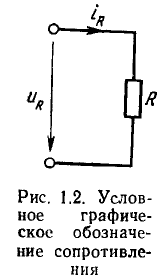
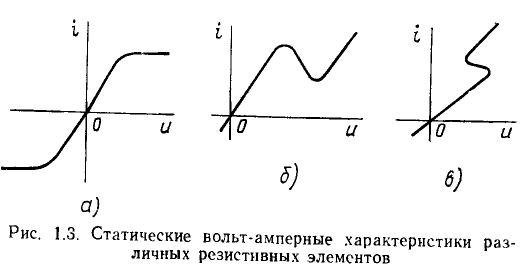
Соответствующие зависимости, полученные для постоянных токов и напряжений, или; точнее, для случая бесконечно медленно изменяющихся токов и напряжений, получили название статических вольт-амперных характеристик (рис. 1.3, а—в). Зависимости между мгновенными значениями тока и напряжения на зажимах резистора называются динамическими вольт-амперными характеристиками.

 Используя зависимость между мгновенными значениями токов и напряжений на зажимах резистора, можно определить его статическое и динамическое сопротивления. Статическое сопротивление — это отношение мгновенных значений напряжения и тока на зажимах резистора:

Динамическое сопротивление резистора определяется производной мгновенного значения напряжения на его зажимах по току:

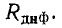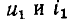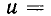
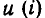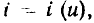Величина, равная динамическому сопротивлению медленном изменении тока и напряжения, получила название дифференциального сопротивления В общем случае динамическое сопротивление резистора не равно статическому, причем значения обеих величин зависят от положения рабочей точки, т. е. от выбора пары значений на характеристике или при которых производится определение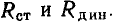

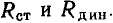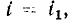
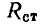Пусть, например, определение производится в рабочей точке (рис. 1.4, а), Значение пропорционально 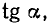т. е. тангенсу угла наклона прямой, проведенной из начала координат в рабочую точку; значение 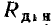пропорционально 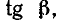т. е. тангенсу угла наклона касательной к кривой 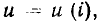в точке  Очевидно, что для рассматриваемого случая 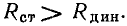Анализируя рис. 1.3, нетрудно убедиться, что в зависимости от выбора рабочей точки значение 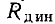может быть как больше, так и меньше нуля, а в частном случае может равняться нулю, в то время как значение 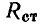всегда больше нуля.

Когда зависимость между напряжением и током на зажимах резистора имеет линейный характер (рис. 1.4, б), значения 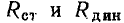не зависят от выбора рабочей точки и равны между собой: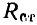 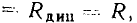 где R - сопротивление резистора.

Резистор, для которого зависимость напряжения от тока имеет линейный характер и, следовательно, значения статического и динамического сопротивлений равны между собой и не зависят от выбора рабочей точки, называется резистором с линейным сопротивлением. Резистор, для которого зависимость 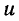 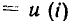или 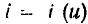имеет нелинейный характер, называется резистором с нелинейным сопротивлением. Следует отметить, что для большинства резисторов зависимост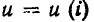и или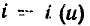 несколько отличаются от линейной, однако в ограниченном диапазоне изменений напряжения этой нелинейностью можно пренебречь и рассматривать сопротивление такого резистора как линейное.

Идеализированный элемент электрической цепи — сопротивление — также характеризуется зависимостью между током и напряжением на его зажимах и определяемыми по этой зависимости значениями статического и динамического сопротивлений. Для линейного сопротивления зависимость между током и напряжением имеет линейный характер, для нелинейного сопротивления эта зависимость отличается от линейной. В дальнейшем, если не будет оговорено особо, ограничимся рассмотрением цепей с линейным сопротивлением.

Зависимость между током и напряжением на зажимах линейного виде подчиняется закону Ома, который можно записать в виде

или

где 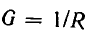— проводимость.

В ряде случаев при исследовании электрических цепей проводимость удобно рассматривать в качестве отдельного идеализированного двухполюсного элемента, имеющего такие же свойства и такое же условное графическое обозначение, как сопротивление, и буквенное обозначение G. Идеализированные элементы электрической цепи сопротивление и проводив относятся к так называемым резистивным  или дисспативным (от латинского dissipare -  рассеивать); наличие  их в цепи приводит к потерям электрической энергии, или, точнее, к  необратимому преобразованию ее в другие виды энергии.

Значения сопротивления R и проводимости G не зависят от выбора рабочей точки, причем R> 0 и G> 0. В Международной системе единиц выражают в омах (Ом), а проводимость в сименсах (См).

Мгновенная мощность сопротивления может быть найдена через значения сопротивления R или проводимости G:

 

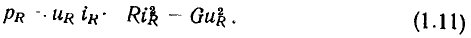
Мгновенная мощность сопротивления при выбранных положительных направлениях тока и напряжения (см.рис.1 2) - положительная величина. Электрическая энергия, поступающая в сопротивление и преобразующая в нем другие формы энергии, также всегда положительная (кроме случая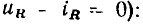 

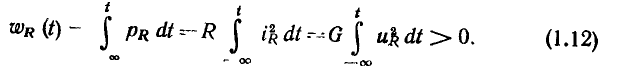
Отметим, что 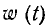 является неубывающей функцией времени (поскольку она вычисляется как площадь, заключенная под кривой  Таким образом, в любой момент времени сопротивление может только потреблять энергию от источников и ни в какие моменты времени сопротивление не может отдавать электрическую энергию другим элементам цепи.

Емкость

Емкостью называется идеализированный элемент электрической цепи, обладающий свойством запасать энергию электрического поля, причем запасания энергии магнитного поля или преобразования электрической энергии в другие виды энергии в ней не происходит. По свойствам к идеализированному элементу — емкости — наиболее близки реальные элементы электрической цепи — конденсаторы. Основной особенностью конденсатора является его способность запасать энергию электрического поля, однако в отличие от идеализированного элемента — емкости —в конденсаторе имеют место потери энергии в диэлектрике и обкладках, т. е. преобразование электрической энергии в другие виды энергии, а также происходит запасание энергии магнитного поля.

Таким образом, термин «емкость» можно использовать как название идеализированного элемента электрической цепи, как характеристику этого элемента, а также как основную характеристику конденсатора, определяющую его способность запасать энергию электрического поля.

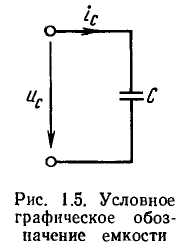
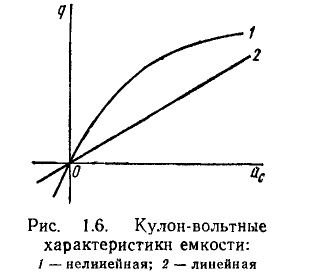
Условное графическое обозначение емкости приведено на рис. 1.5. Зависимость заряда q, накопленного в емкости, от напряжения 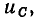называемая кулон-вольтной характеристикой, имеет в общем случае нелинейный характер (рис. 1.6, кривая 1).

Количественно зависимость заряда, накопленного в емкости, от напряжения оценивают значениями статической и динамической емкостей:

В общем случае динамическая емкость не равна статической, причем обе величины зависят от выбора рабочей точки на характеристике q = q (u). Если зависимость заряда, накопленного в емкости, от напряжения имеет линейный характер (рис. 1 6, кривая 2), то значения динамической и статической емкостей равны и не зависят от напряжения: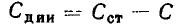

В системе единиц СИ емкости 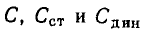выражают в фарадах (Ф).

Емкость, значение которой не зависит от напряжения, называется линейной; емкость, значение которой зависит от напряжения — нелинейной. В дальнейшем, если не будет сделано особых оговорок, ограничимся рассмотрением только цепей с линейной емкостью.

Найдем зависимость между мгновенными значениями тока и напряжения на зажимах линейной емкости. Очевидно, что всякое изменение напряжения 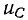на зажимах емкости должно, в соответствии с видом зависимости  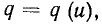привести к изменению заряда q. Производная заряда по времени определяет ток емкости

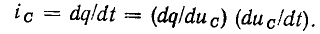
Учитывая, что для линейной емкости производная заряда по напряжению равна С и не зависит от напряжения 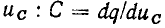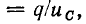получаем

Как видно из выражения (1.13), ток емкости пропорционален скорости изменения ее напряжения. Если напряжение на зажимах емкости не изменяется во времени, то ток емкости равен нулю. Таким образом, сопротивление емкости постоянному току бесконечно велико. Используя выражение (1.13), находим зависимость напряжения от емкости тока: 

Интегрирование ведется начиная с момента времени 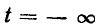для того, чтобы учесть все возможные изменения заряда емкости и, следовательно, напряжения 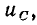причем предполагается, что в момент времени  напряжение на зажимах емкости равно нулю.

Пусть наблюдение процессов в емкости началось в момент 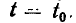Напряжение емкости в начальный момент

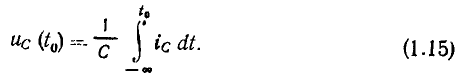
Разбивая интеграл (1.14) на два: 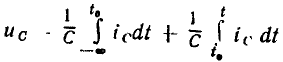 и используя выражение (1.15), находим напряжение на емкости в произвольный момент времени t:

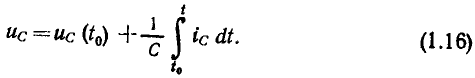
Мгновенная мощность емкости

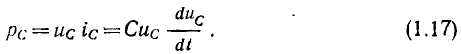
Если напряжение на емкости (см. рис. 1.5) положительно (т. е. его направление совпадает с условно-положительным направлением, указанным стрелкой) и продолжает возрастать, то мгновенная мощность емкости в соответствии с (1.17) будет положительной. В этом случае энергия поступает в емкость, т. е. она заряжается.

Если 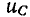>0 и убывает, т. е. 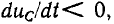то мгновенная мощность емкости отрицательна. Емкость при этом разряжается, т. е. отдает накопленную энергию во внешнюю цепь.

Энергия электрического поля, запасенная емкостью в произвольный момент времени t, определяется напряжением емкости или ее зарядом:

 

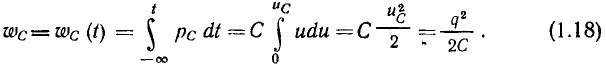
Очевидно, что в любой момент времени t энергия, запасенная в емкости, будет неотрицательной величиной.

Таким образом, емкость является пассивным идеализированным элементом электрической цепи, который в зависимости от режима работы может либо запасать энергию электрического поля, получаемую из внешней по отношению к емкости цепи, либо отдавать накопленную энергию во внешнюю цепь.

Индуктивность

Индуктивностью называется идеализированный элемент электрической цепи, в котором происходит запасание энергии магнитного поля. Запасания энергии электрического поля или преобразования электрической энергии в другие виды энергии в ней не происходит. Наиболее близким к идеализированному элементу— индуктивности — является реальный элемент электрической цепи — индуктивная катушка. В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электрического поля и преобразование электрической энергии в другие виды энергии, в частности в тепловую. Количественно способность реального и идеализированного элементов электрической цепи запасать энергию магнитного поля характеризуется параметром, называемым индуктивностью.

Таким образом термин «индуктивность» применяется как название идеализированного элемента электрической цепи, как название параметра, количественно характеризующего свойства этого элемента, и как название основного параметра индуктивной катушки.

Условное графическое обозначение индуктивности приведено на рис. 1.7.

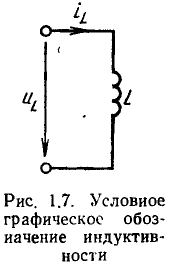
Связь между напряжением и током в индуктивной катушке определяется законом электромагнитной индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости изменения потокосцепления катушки 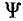и направленная таким образом, чтобы вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:

Потокосцепление катушки равно алгебраической сумме магнитных потоков 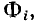пронизывающих ее отдельные витки:

где N — число витков катушки.

Если магнитный поток, пронизывающий все витки катушки, одинаков выражение (1.20) приводится к виду

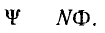
В системе единиц СИ магнитный поток и потокосцепление выражают в веберах (Вб).

Магнитный поток Ф, пронизывающий каждый из витков катушки, в общем случае может содержать две составляющие: магнитный поток самоиндукции 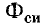и магнитный поток внешних полей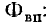

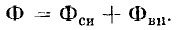
Первая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током; вторая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и постоянных магнитов. Если вторая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее называют магнитным потоком взаимоиндукции.

Потокосцепление катушки 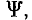так же как и магнитный поток Ф, может быть представлено в виде суммы двух составляющих: потокосцепления самоиндукции 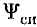и потокосцепления внешних полей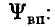

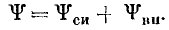
Наведенная в индуктивной катушке э. д. с. е, в свою очередь, может быть представлена в виде суммы э. д. с. самоиндукции, которая вызвана изменением магнитного потока самоиндукции, и э. д. с., вызванной изменением магнитного потока внешних по отношению к катушке полей:

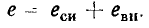
Здесь 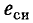— э. д. с. самоиндукции; 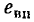— э. д. с. внешних полей.

Если магнитные потоки внешних по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только э. д. с. самоиндукции

Потокосцепление самоиндукции 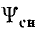зависит от протекающего по катушке тока 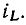Эта зависимость, называемая вебер- амперной характеристикой индуктивной катушки, в общем случае имеет нелинейный характер (рис. 1.8, кривая 1). В частном случае, например для катушки без магнитного сердечника, эта зависимость может быть линейной (рис. I 8, кривая 2). Количественно зависимость потокосцепления самоиндукции от тока определяется статической 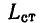и динамической 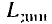индуктивностями катушки:

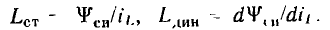
Значения 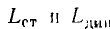в общем случае не равны между собой и зависят от выбора рабочей точки (значения тока 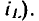При линейной зависимости потокосцепления самоиндукции от тока статическая и динамическая индуктивности катушек равны и не зависят от выбора рабочей точки: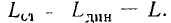

В системе единиц СИ индуктивности 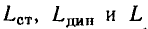выражают в генри (Гн). В дальнейшем, если не будет сделано особых оговорок, ограничимся рассмотрением только цепей с линейной индуктивностью.

Для катушки с линейной индуктивностью выражение (1.21) может быть преобразовано к виду

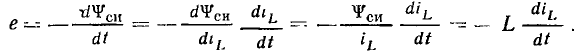
При анализе цепей обычно рассматривают не значение э. д. с., наведенной в катушке, а напряжение 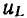 на ее зажимах, положительное направление которого выбирают совпадающим с положительным направлением тока (см. рис. 1.7):

Идеализированный элемент электрической цепи — индуктивность, можно рассматривать как упрощенную модель индуктивной катушки, отражающую способность катушки запасать энергию магнитного поля. Для линейной индуктивности напряжение 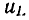на ее зажимах пропорционально скорости изменения тока 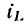и определяется выражением (1.22). При протекании через индуктивность постоянного тока напряжение на ее зажимах равно нулю, следовательно, сопротивление индуктивности постоянному току равно нулю.

Зависимость тока индуктивности 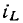от напряжения 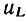может быть найдена путем интегрирования выражения (1.22):

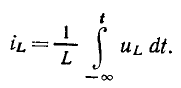
Чтобы учесть все изменения напряжения на индуктивности, имевшие место до рассматриваемого момента времени t, интегрирование ведется начиная с причем принимается, что при 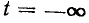  ток индуктивности равен нулю. В момент времени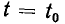

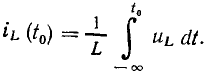
При известном значении 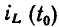 интегрирование (1.22) в пределах от  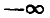до t может быть заменено интегрированием в пределах  от  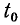до t:

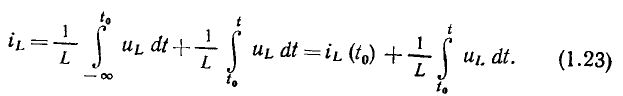
 Мгновенная мощность индуктивности 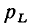определяется произведением мгновенных значений тока  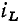и напряжения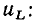

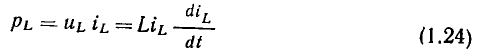
и будет положительной в моменты времени, когда индуктивность потребляет энергию от остальной части цепи 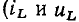 имеют одинаковый знак). В моменты времени, когда 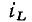и 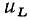имеют различные знаки, индуктивность отдает запасенную ранее энергию остальной части цепи, т.е.  

Энергия, запасенная в индуктивности в произвольный момент времени t:

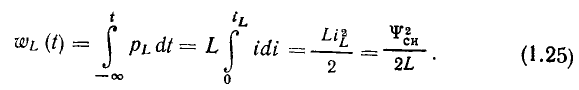
Таким образом, энергия, запасенная в индуктивности, является неотрицательной величиной и определяется только током индуктивности или потокосцеплением самоиндукции.

Идеализированные элементы электрической цепи (емкость и индуктивность), способные запасать энергию электрического или магнитного полей, называются энергоемкими или реактивными.

Дуальные элементы и цепи

Рассматривая полученные ранее соотношения (табл. 1.1), приходим к заключению, что выражения, соответствующие попарно сопротивлению и проводимости, емкости и индуктивности, имеют подобную структуру. Если в выражениях, описывающих основные соотношения для сопротивления, заменить 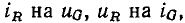R на G, то получатся основные соотношения для проводимости. Аналогично, выражения, описывающие основные соотношения для емкости и индуктивности, могут быть получены одно из другого путем замены 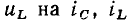на 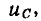L на С. Элементы, для которых основные соотношения имеют одинаковую структуру и могут быть получены одно из другого путем таких замен, называются дуальными. Таким образом, емкость и индуктивность, сопротивление и проводимость (попарно) являются дуальными элементами.

Свойством дуальности обладают не только рассмотренные идеализированные пассивные элементы. Из последующих разделов будет видно, что дуальными также могут быть идеализированные активные элементы и электрические цепи, составленные из идеализированных активных и пассивных элементов.

В ряде случаев использование принципа дуальности позволяет облегчить исследование процессов в цепи. Так. если известны основные соотношения, описывающие процессы в некоторой цепи, то соответствующие соотношения для дуальной цепи могут быть получены без вывода, на основании использования свойства дуальности.

Схемы замещения реальных элементов электрических цепей

При описании идеализированных пассивных элементов электрических цепей подчеркивалось, что каждый из этих элементов отражает только одну существенную особенность электромагнитных процессов, имеющих место в реальных элементах электрических цепей.

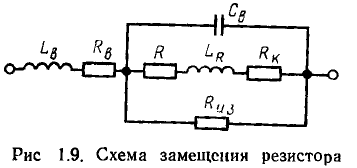
Каждый из рассмотренных идеализированных элементов имеет в качестве «прототипа» реальный пассивный элемент: резистор, индуктивную катушку или конденсатор. В то же время отмечалось, что процессы в реальных элементах существенно сложнее, чем в идеализированных, в частности в каждом реальном элементе наряду с основным имеют место также другие, так называемые паразитные процессы. Вследствие этого схемы замещения реальных элементов в общем случае состоят из идеализированных элементов различных типов.

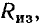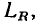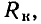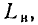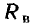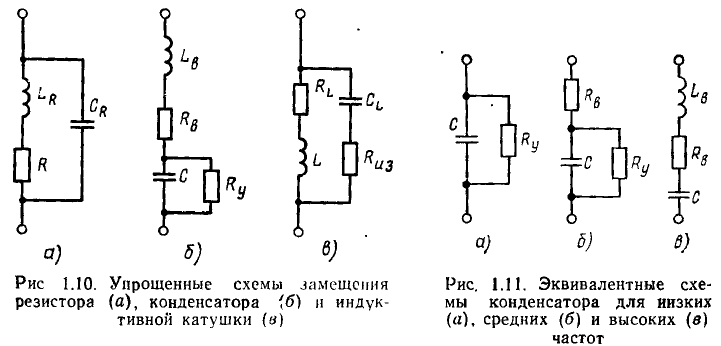
На рис. 1.9 в качестве примера приведена схема замещения резистора, в которой наряду с основным элементом — сопротивлением токонесущего слоя R — содержатся паразитные элементы: сопротивление изоляции индуктивность токонесущего слоя сопротивление контактов индуктивность выводов сопротивление выводов и емкость между выводами 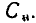Вид эквивалентной схемы и параметры входящих в нее идеализированных элементов существенным образом зависят от конструкции реального элемента, технологии его изготовления и особенностей применяемых материалов. Чем выше требуемая точность расчетов, тем большее количество факторов должно быть принято во внимание и тем более сложный вид будет иметь эквивалентная схема каждого элемента. Вместе с тем излишнее усложнение эквивалентных схем существенно увеличивает трудоемкость расчетов, вследствие чего при исследовании цепей стремятся использовать упрощенные эквивалентные схемы, содержащие минимально допустимое число элементов (рис. 1.10).

Следует отметить, что схемы замещения одного и того элемента могут иметь различный вид в зависимости от рассматриваемого диапазона частот (рис. 1.11). Так, на довольно низких частотах при невысоких требованиях к точности расчетов эквивалентная схема индуктивной катушки может состоять только из индуктивности, характеризующей способность катушки запасать энергию магнитного поля, и сопротивления, отражающего все виды потерь в ней. При этих же условиях эквивалентная схема резистора может состоять из одного элемента — сопротивления.