
Гравитационные силы в физике - формулы и определение с примерами
Гравитационные силы:
В механике изучают силы тяготения или гравитационные силы, силы упругости и силы трения.
Гравитационная сила является проявлением закона всемирного тяготения, который сформулировал Ньютон: гравитационное притяжение существует между всеми телами; любые два тела, размерами которых можно пренебречь, притягиваются друг к другу с силой, которая прямо пропорциональна массам этих тел и обратно пропорциональна квадрату расстояния между ними (рис. 2.10):
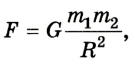
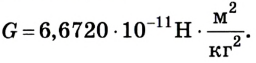
Ее числовое значение впервые определил путем эксперимента английский ученый Г. Кавендиш в 1798 г.
Закон всемирного тяготения справедлив для точечных тел, размеры которых намного меньше расстояния между ними, а также для больших однородных шаров, например, системы Земля-Луна, или однородного шара и точечного тела (движение искусственного спутника вокруг Земли). Гравитационная сила в данном случае направлена вдоль линии, которая соединяет центры масс взаимодействующих тел.
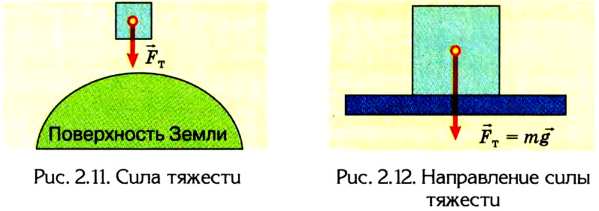
Гравитационная сила, с которой Земля притягивает к себе тела, придавая им ускорение свободного падения, называется силой тяжести (рис. 2.11):
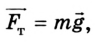
где m - масса тела; 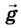 - ускорение свободного падения, числовое значение которого зависит от географической широты нахождения тела и высоты над земной поверхностью (уровнем моря).
- ускорение свободного падения, числовое значение которого зависит от географической широты нахождения тела и высоты над земной поверхностью (уровнем моря).
Сила тяжести всегда приложена к центру масс тела и направлена вертикально вниз, перпендикулярно к горизонтальной поверхности (рис. 2.12).
При решении задач по физике достаточно часто используют понятие веса тела, т. е. силы, с которой тело действует на подставку или подвес вследствие притяжения Земли (рис. 2.13).
Если тело в инерциальной системе отсчета неподвижно или движется равномерно и прямолинейно, то его вес равен силе тяжести: 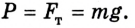
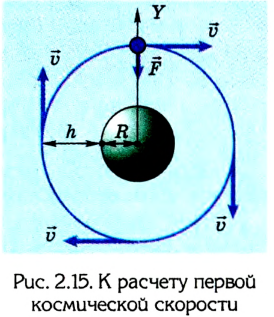
При равноускоренном движении тела вверх или вниз с ускорением 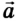 вес тела изменяется на
вес тела изменяется на  (рис. 2.14).
(рис. 2.14).
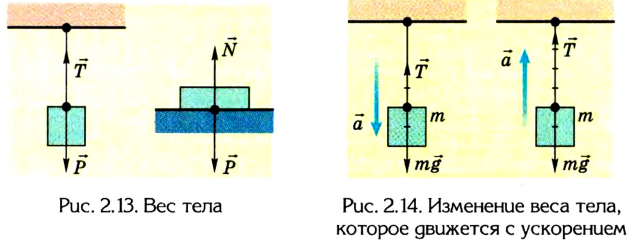
Т. е., во время движения вниз Р = m(g - а), а во время движения вверх Р = m(g + а). В случае свободного падения (а = g) тела находятся в состоянии невесомости, их вес равен нулю (Р = 0).
Масса характеризует инертные и гравитационные свойства тел.
Если во втором законе механики масса характеризует инертные свойства тел, то в законе всемирного тяготения - их гравитационные свойства.
Рассмотрим пример решения задачи на действие гравитационной силы.
Пример решения задачи:
Какую скорость нужно сообщить телу, чтобы оно стало искусственным спутником планеты массой М, радиус которой R, и вращалось по орбите на высоте h?
Решение
В задаче четко определен характер движения тела: траектория движения - окружность; скорость - постоянная; направление скорости в каждой точке траектории - по касательной. Сила гравитационного взаимодействия искусственного спутника с планетой вызывает центростремительное ускорение.
Сделаем рисунок в соответствии с условием задачи (рис. 2.15).
Будем считать, что планета имеет форму шара, а спутник не испытывает действия сил сопротивления.
Таким образом, на спутник действует лишь сила гравитационного притяжения к планете:
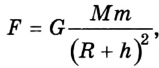
где М - масса планеты; m - масса спутника; G - гравитационная постоянная.
Как правило, во время движения по окружности выбирают ось координат ОУ так, чтобы она была направлена к центру окружности или, наоборот, от него.
Для искусственного спутника планеты запишем уравнение второго закона механики Ньютона в векторной форме: 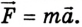
Затем это уравнение представим в скалярной форме, определив направления гравитационной силы и ускорения: -F = -mа.
Поскольку скорость спутника постоянна (по значению), то сила притяжения к планете придает ему лишь центростремительное ускорение 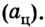 Итак, мы имеем систему уравнений:
Итак, мы имеем систему уравнений:
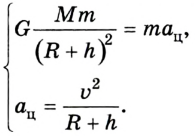
Данная система уравнений легко решается методом подстановки: 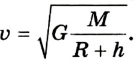
Искомая скорость будет одинаковой для спутников различной массы, поскольку не зависит от нее. Например, для любой планеты она будет зависеть лишь от высоты спутника над ее поверхностью.
Чтобы найти значение скорости тела, которая необходима искусственному спутнику планеты, т. е. первой космической скорости, воспользуемся параметрами Земли: 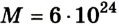 кг, R- 6400 км, h = 300 км. Подставив их в формулу, получим v= 7,7 км/с.
кг, R- 6400 км, h = 300 км. Подставив их в формулу, получим v= 7,7 км/с.
Ответ: v = 7,7 км/с (для Земли).
Гравитационные силы. Закон всемирного тяготения. Сила тяжести. Ускорение свободного падения
Сила тяжести, действующая на тело, прямо пропорциональна его массе: 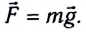 Направление силы тяжести принимают за направление вертикали в данной точке земной поверхности.
Направление силы тяжести принимают за направление вертикали в данной точке земной поверхности.
В большинстве механических процессов силы возникают при непосредственном (механическом) контакте взаимодействующих тел. Это справедливо, например, в случае сил упругости, трения, реакции опоры.
Однако сила гравитационного взаимодействия способна действовать на расстоянии, т. е. она существует даже тогда, когда тела не находятся в контакте.
Гравитационные силы (силы тяготения) — это силы, с которыми притягиваются друг к другу все тела во Вселенной.
Модуль и направление гравитационных сил определяется законом всемирного тяготения:
- две материальные точки притягиваются друг к другу с силой
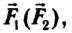 прямо пропорциональной произведению их масс
прямо пропорциональной произведению их масс 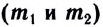 и обратно пропорциональной квадрату расстояния
и обратно пропорциональной квадрату расстояния 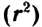 между ними. Силы
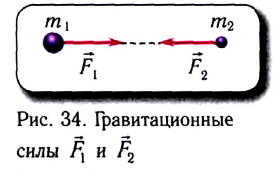
между ними. Силы 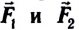 направлены вдоль прямой, соединяющей материальные точки (рис. 34):
направлены вдоль прямой, соединяющей материальные точки (рис. 34):
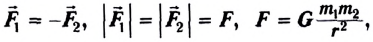
где 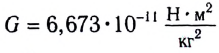 — гравитационная постоянная.
— гравитационная постоянная.
Заметим, что гравитационная постоянная численно равна силе, с которой взаимодействуют две материальные точки массами 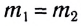 = 1,000 кг, находящиеся на расстоянии r= 1,000 м друг от друга.
= 1,000 кг, находящиеся на расстоянии r= 1,000 м друг от друга.
Впервые гравитационную постоянную G измерил в 1798 году Г. Кавендиш с помощью крутильных весов.
Закон всемирного тяготения справедлив не только для двух материальных точек, но и для тел произвольной формы, размеры которых во много раз меньше расстояний между центрами тяжести тел, а также для тел шарообразной формы, где под расстоянием r понимается расстояние между центрами шаров.
Гравитационные силы обусловлены взаимным притяжением тел, рассматриваемых как материальные точки. Они направлены вдоль линии, соединяющей взаимодействующие материальные точки, и поэтому называются центральными силами.
В основе вывода закона всемирного тяготения лежат законы Кеплера, второй закон Ньютона и предположение об универсальности взаимодействия между телами независимо от их природы.
Гравитационное взаимодействие может быть описано с помощью гравитационного поля (поля сил тяготения). Тело массой 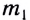 может рассматриваться как источник гравитационного поля, которое притягивает тело массой
может рассматриваться как источник гравитационного поля, которое притягивает тело массой 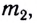 находящееся на расстоянии r от него, с силой, модуль которой равен
находящееся на расстоянии r от него, с силой, модуль которой равен 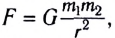 и направленной по прямой, соединяющей центры масс этих тел. Аналогично можно рассматривать тело массой
и направленной по прямой, соединяющей центры масс этих тел. Аналогично можно рассматривать тело массой 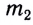 как источник гравитационного поля, в котором находится тело массой
как источник гравитационного поля, в котором находится тело массой 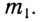
На тело, находящееся в гравитационном поле Земли, действует сила всемирного тяготения 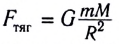 (m — масса тела, М — масса Земли, R — радиус Земли), направленная к центру Земли (рис. 35). В этом случае Землю считаем однородным шаром радиусом R.
(m — масса тела, М — масса Земли, R — радиус Земли), направленная к центру Земли (рис. 35). В этом случае Землю считаем однородным шаром радиусом R.
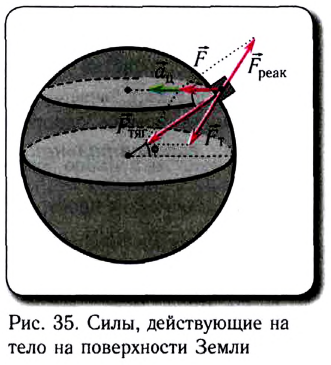
Согласно второму закону Ньютона при вращательном движении вместе с Землей на тело со стороны Земли действует результирующая сила
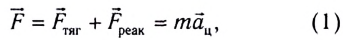
где 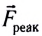 — сила суммарной реакции земной поверхности,
— сила суммарной реакции земной поверхности, 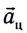 — центростремительное (нормальное) ускорение.
— центростремительное (нормальное) ускорение.
Составляющая силы всемирного тяготения, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения 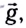 называется силой тяжести. Так как угловая скорость вращения Земли мала
называется силой тяжести. Так как угловая скорость вращения Земли мала 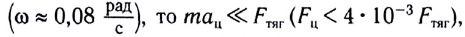 поэтому сила тяжести
поэтому сила тяжести 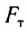 незначительно отличается от силы гравитационного притяжения Земли и по модулю, и по направлению, т.е.
незначительно отличается от силы гравитационного притяжения Земли и по модулю, и по направлению, т.е. 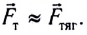
Точку приложения силы тяжести называют центром тяжести тела. Положение центра тяжести тела в однородном гравитационном поле совпадает с его центром масс.
По второму закону Ньютона 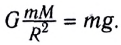
Откуда ускорение свободного падения 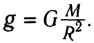
Следовательно, ускорение свободного падения g не зависит от массы m тела, а определяется массой Земли М и ее радиусом R.
Ускорение свободного падения зависит от:
широты  данной точки (Земля — неинерциальная система отсчета) земной
данной точки (Земля — неинерциальная система отсчета) земной
- поверхности (на полюсе
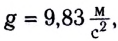 на экваторе
на экваторе 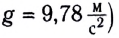 и пород земной коры;
и пород земной коры; - высоты h над поверхностью Земли
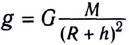 (докажите самостоятельно); формы Земли (она приплюснута у полюсов).
(докажите самостоятельно); формы Земли (она приплюснута у полюсов).
При подъеме тела сила тяжести убывает с высотой сравнительно медленно. Так, на высоте 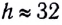 км над поверхностью Земли она уменьшается всего на 1 %.
км над поверхностью Земли она уменьшается всего на 1 %.
Нормальным ускорением свободного падения называется ускорение свободного падения на широте 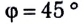 на уровне моря (h = 0), измеренное при нормальных условиях. Численно оно равно
на уровне моря (h = 0), измеренное при нормальных условиях. Численно оно равно 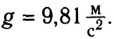
Гравитационное поле, в котором на материальную точку массой m в любой точке пространства действует одинаковая сила 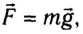 называется однородным.
называется однородным.
В рамках модели однородного гравитационного поля поверхность Земли считается горизонтальной, а сила тяжести направлена вертикально вниз.
В малых областях пространства вблизи поверхности Земли и других небесных тел такая модель применима для описания гравитационного поля. Однородное гравитационное поле называется полем тяжести.
Таким образом, ускорение свободного падения g — это ускорение, с которым движется материальная точка вблизи поверхности Земли под действием силы тяжести, в системе отсчета, связанной с Землей как телом отсчета.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |