Гранные поверхности в начертательной геометрии с примерами

Содержание:

Многогранники и их изображение на эпюре Монжа:

Многогранниками называются замкнутые пространственные фигуры, ограниченные плоскими многоугольниками вершины и стороны
которых являются вершинами и ребрами многогранника. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранники называются выпуклыми.

Многогранники с древнейших времен получили широкое распространение в техническом творчестве людей. Многие памятники архитектуры, дошедшие до наших дней, имеют форму многогранников: египетские пирамиды, многие башни и здания, храмы и замки. Огромное количество примеров неповторимого сочетания гранных поверхностей имеется в русском национальном творчестве.

Гранные поверхности широко применяются и в наши дни в конструкциях современных зданий и других инженерных сооружений. Так,
например, крыши жилых, общественных и промышленных зданий часто представляют собой пересекающиеся призмы и пирамиды.
Многогранники в виде оптических призм используют и в технической оптике, где приходится решать инженерные задачи, связанные с
проектированием оптических приборов и с учетом физических явлений преломления и отражения лучей при их падении на границу раз-
дела двух сред.

В природе форму многогранников имеют кристаллы, из которых состоят не только вещества, слагающие горные породы, но и все металлы и сплавы, кости, зубы, волосы, перья, хлопок и т.д.)

Наибольший практический интерес представляют призмы, пирамиды, призматоиды и правильные выпуклые многогранники (так называемые тела Платона, тетраэдр, гексаэдр, октаэдр, додекаэдр,икосаэдр и др.), а также многогранники произвольной формы.

Охарактеризуем кратко геометрические тела каждой из перечисленных групп.

Пирамиды

Многогранник, одна грань которого - многоугольник со сколь угодно большим числом сторон (не менее трех), а остальные грани - треугольники с общей вершиной, называется пирамидой (рис. 3.1).

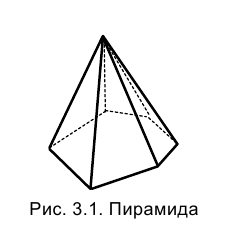
Если в основании пирамиды лежит правильный многоугольник и ее высота (перпендикуляр, опущенный из вершины на основание) проходит через центр этого многоугольника, пирамиду называют правильной.

Пирамиду можно получить пересечением многогранного угла произвольной плоскостью. Отсеченная часть многогранного угла вместе с
фигурой сечения образует пирамиду. Если плоскостью, пересекающей все боковые ребра, отсечь вершину пирамиды, получим усеченную пирамиду.
 

Призмы

Многогранник, две грани которого представляют собой равные многоугольники с взаимно параллельными сторонами основаниями, называют призмой. Ребра, не принадлежащие плоскостям оснований и параллельные между собой, называются боковыми. Основания образуются одно из другого параллельным переносом. Соответствующие вершины соединяются между собой прямыми, которые образуют параллелограммы, являющиеся боковыми гранями призмы.
На рис. 3.2 приведен пример по- строения призмы ограниченной двумя горизонтальными плоскостями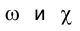

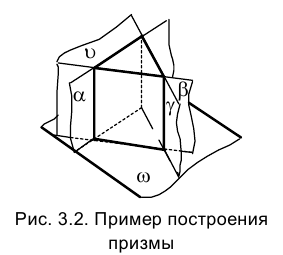
Если ребра призмы перпендикулярны плоскости ее основания, то призма называется прямой. Если основание призмы – прямоугольник призма называется параллелепипедом.

Изображение многогранников на эпюре Монжа Как и чертежи любых других пространственных объектов, чертежи многогранников должны быть обратимыми, т.е. такими, чтобы по ним можно было точно воспроизвести форму и размеры изображаемого предмета.

При изображении многогранников на эпюре Монжа необходимо показывать видимость геометрических элементов, при этом невидимые ребра вычерчивают штриховой линией.

Для иллюстрации изображения многогранников на эпюре Монжа рассмотрим два их типа - призмы и пирамиды. Основания призм и пирамид обычно представляются плоскостями общего положения, произвольно наклоненными к боковым граням и ребрам. Ясно, что
многогранник может занимать в пространстве любое положение относительно плоскостей проекций 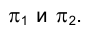. Для удобства выполнения построений на эпюре Монжа будем предполагать, что плоскости их оснований проецирующие.

На рис. 3.3 приведены примеры изображения трехгранных и пирамид на эпюре Монжа. Из текста следует, что название рассматриваемой призмы и пирамиды определяется числом новых граней. Видимость ребер многогранников определяется из следующих соображений: внешний контур проекции всегда видим: определение же видимости ребер, проецирующихся внутри проекции контура призмы на плоскостях , требует рассмотрения обеих проекций.

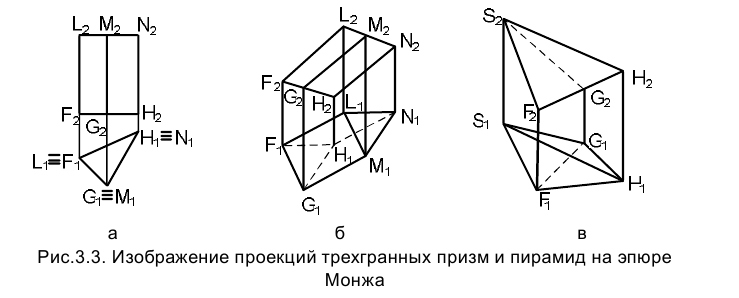
Так, например, анализируя изображения горизонтальной проекции нижнего основания призмы в обоих приведенных на рис.
3.3, а, б случаях приходим к выводу, что ребро GМ как наиболее удаленное от плоскости будет на плоскости 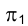видимым и его проекция 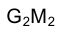должна быть показана сплошной основной линией.

Горизонтальные проекции 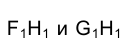сторон нижнего основания и ребра HN наклонной призмы нужно изобразить штриховой линией, поскольку они закрываются гранью 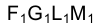и верхним основанием призмы, что легко заметить, если посмотреть на призму в направлении, перпендикулярном плоскости 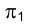(сверху).

При построении наклонной пирамиды SFGН на эпюре Монжа фронтальную проекцию ребра SG следует показать штриховой линией, так как из рассмотрения горизонтальной проекции основания пирамиды видно, что вершина G расположена ближе к фронтальной плоскости проекций 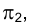, чем сторона FН основания, и закрывается ею. На горизонтальной же проекции пирамиды штриховой линией нужно показать проекцию 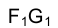стороны основания FG, поскольку она закрыта гранями 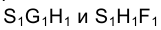(рис. 3.3,в).
Рассмотрим построение на эпюре Монжа проекции произвольной точки, принадлежащей поверхности многогранника на примере призмы и пирамиды. Поскольку принадлежащая поверхности многогранника точка лежит либо в плоскости одной из его боковых граней, либо в плоскости одного из оснований, для задания ее проекций на эпюре следует построить проекции произвольной прямой, проходящей через эту точку в пространстве и принадлежащей плоскости соответствующей боковой грани или основания.

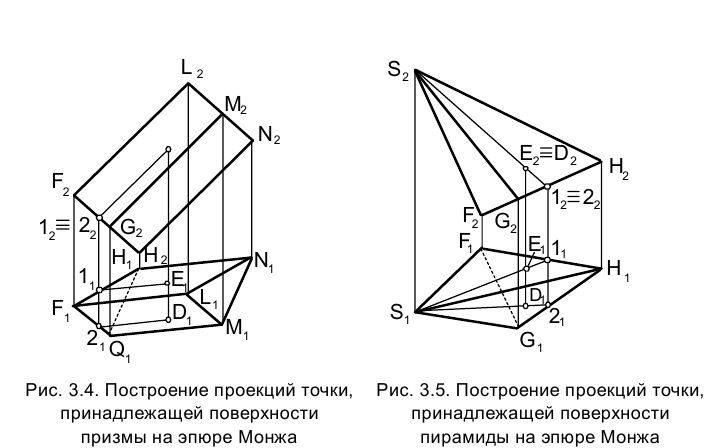
Принципы построения проекций прямой линии, принадлежащей плоскости, рассмотрены выше в разделе 1.5. В случае построения проекций точки, принадлежащей поверхности призмы, удобно в качестве проходящей через нее прямой воспользоваться прямой, параллельной боковым ребрам призмы (рис. 3.4), а в случае принадлежности точки поверхности пирамиды - прямой, проходящей через вершину последней (рис. 3.5).

Построим горизонтальную проекцию точки Е, принадлежащей боковой поверхности призмы LМNFGH, если задана ее фронтальная проекция 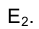 Через фронтальную проекцию точки Е – 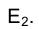строим фронтальную проекцию прямой 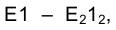, параллельной ребрам призмы. Из рис. 3.4 следует, что прямой 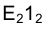на фронтальной плоскости проекций 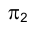на горизонтальной плоскости проекций 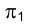соответствуют две прямые 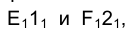, а следовательно, точке 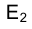на фронтальной плоскости проекций 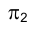ответствуют две точки 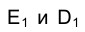на горизонтальной плоскости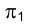

Такая ситуация естественна, поскольку точка 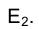на фронтальной плоскости проекций 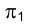является, по существу, фронтальной проекцией двух точек Е и D, принадлежащих различным граням призмы FLМG и FLNН и лежащих на одной прямой, перпендикулярной к плоскости 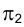. Следовательно, и прямая 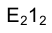является фронтальной проекцией двух прямых, параллельных ребрам призмы и лежащих в ее гранях.

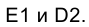Для того чтобы приведенное на рис. 3.4 изображение соответствовало пространственной ситуации, мы должны привести в соответствие обозначение на эпюре Монжа, что и сделано на рис. 3.6.
На рис. 3.5 показано построение проекций точек, принадлежащих боковой поверхности трехгранной пирамиды

Пересечений многогранников плоскостью и прямой линией

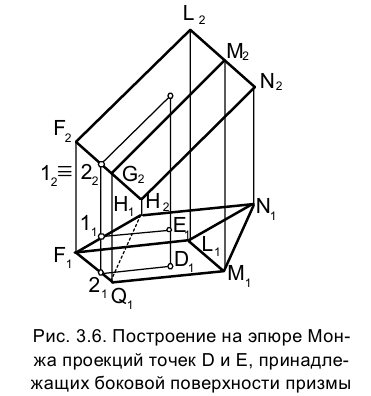
При пересечении произвольной поверхности или тела плоскостью получается некоторая плоская фигура, называемая сечением. Сечение многогранника может быть ограничено только отрезками прямых, т.е. является многоугольником. Число сторон такого многоугольника равно числу граней многогранника, пересекаемых секущей плоскостью. Так, например, в зависимости от направления секущей плоскости сечением куба может быть треугольник, четырехугольник, пятиугольник и шестиугольник (рис. 3.7).
Вершинами многоугольника сечения являются точки пересечения ребер многогранника с секущей плоскостью. Поэтому число вершин многоугольника равно числу ребер многогранника, пересекаемых секущей плоскостью.

Различают два способа построения плоского сечения многогранника:

• 1) отыскание вершин n -угольника сечения (способ ребер);
• 2) отыскание сторон n -угольника сечения (способ граней).

При первом способе построение сводится к решению позиционной задачи 4 - нахождению точки пересечения прямой с плоскостью, при втором способе - к нахождению линии пересечениях двух плоскостей (позиционная задача 5).
Итак, рассмотрим задачу о пересечении многогранника - призмы FGHLMN - с фронтально проецирующей плоскостью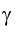(рис. 3.8).

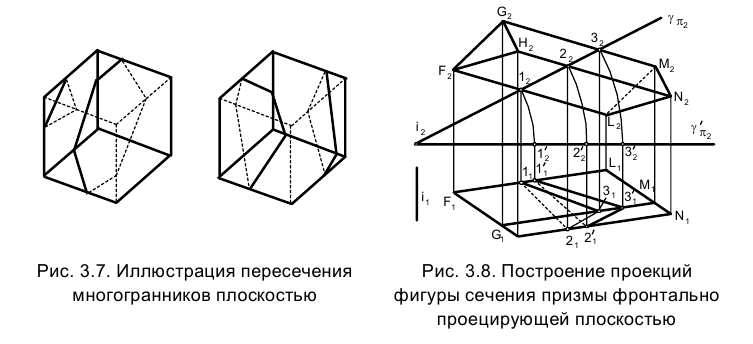
Для нахождения решения задачи воспользуемся способом ребер. Действительно, следует найти точки встречи ребер FL, HN и GМ призмы с проецирующей плоскостью 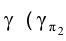-след плоскости g на фронтальной плоскости проекций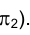

На эпюре Монжа (см. рис. 3.8) горизонтальные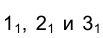 проекции точек 1, 2 и 3 определяют горизонтальную проекцию треугольника 123, являющегося пространственным сечением призмы.

Для определения истинной величины сечения следует воспользоваться, например, рассмотренным выше способом вращения геометрических образов относительно осей перпендикулярных плоскостям проекций (раздел 1.7).

В данном случае выбираем ось вращения ί, перпендикулярную фронтальной плоскости проекций 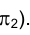, и поворачиваем вокруг нее след плоскости 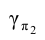до положения, параллельного направлению оси проекций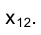. Тогда смещенная горизонтальная проекция 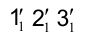треугольника 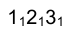определит на горизонтальной плоскости проекций истинную величину сечения.

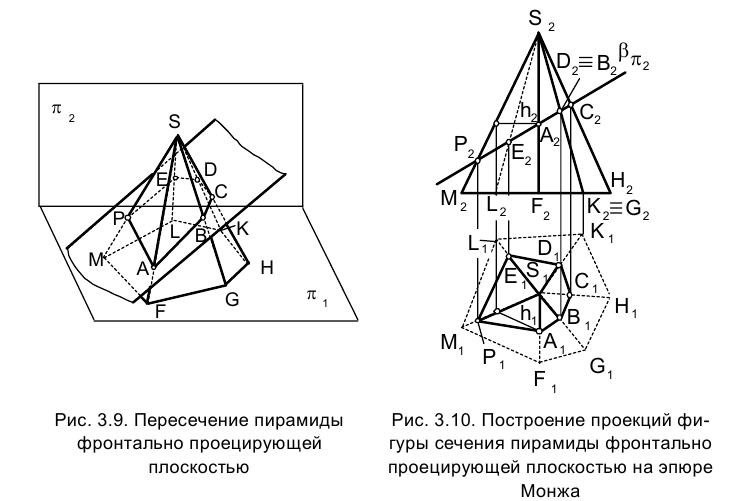
На рис. 3.9 приведен пример пересечения фронтально проецирующей плоскостью 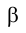пирамиды SFGHKLM. Как видно из рассмотрения условия задачи, на эпюре Монжа (рис. 3.10) фронтальная проекция многоугольника сечения АВСDЕР вырождается в отрезок прямой, совпадающей со следом плоскости 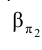на фронтальной плоскости проекций.

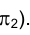Используя метод ребер, находим горизонтальные проекции вершин многоугольника сечения. Поскольку одно из ребер SF, на котором лежит вершина S, является отрезком профильной прямой, для построения горизонтальной проекции точки A – 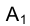построим в грани SМF вспомогательную горизонталь. Соединяя последовательно отрезками прямых точки 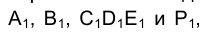, получим горизонтальную проекцию сечения - выпуклый шестиугольник. Используя метод вращения относительно оси ί, перпендикулярной плоскости проекций 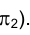, определим истинную величину шестиугольника сечения.

Рассмотрим, наконец, случай пересечения многогранника призмы FGНLМN плоскостью общего положения 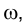, заданной пересекающимися прямыми q и r (рис. 3.11).

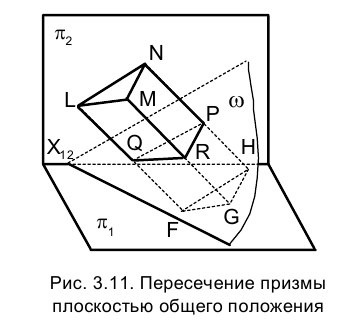
Применив, как и в двух предыдущих случаях, способ ребер, определим точки пересечения каждого из ребер призмы с плоскостью 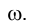В качестве вспомогательных проецирующих плоскостей используем
проходящие через ребра призмы горизонтально проецирующие плоскости 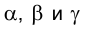соответственно (рис. 3.12). Линии пересечения этих плоскостей с плоскостью 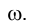определяются отрезками прямых 12, 34 и 56. Точки, в которых эти отрезки пересекаются с ребрами призмы, и являются вершинами треугольника сечения QRР.

Поскольку на обе плоскости проекций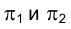 треугольник сечения проецируется с искажением, для определения его истинной формы следует применить один из известных нам способов (треугольника, замены плоскостей проекций, вращения).

В качестве практических примеров, иллюстрирующих рассмотренные выше задачи, можно привести случаи изменения формы сечения
вентиляционных воздухопроводов сложной конфигурации. Весьма важной задачей, решение которой широко используется при проектировании составных гранных поверхностей, является задача о пересечении прямой линии с поверхностью многогранника.

В общем случае прямая линия может пересекать поверхность многогранника в одной, двух и более точках, однако любой выпуклый многогранник - не более, чем в двух точках. Точки пересечения прямой с многогранником называют часто точками встречи.

Общий способ нахождения точек встречи прямой с поверхностью многогранника состоит в многократном использовании алгоритма решения позиционной задачи 4 (раздел 1.5) - определения точки встречи прямой с плоскостью.

Через заданную прямую проводят вспомогательную (как правило, проецирующую) плоскость и строят линии ее пересечения с каждой из граней многогранника - стороны многоугольника сечения. Искомые точки встречи определяются как точки пересечения заданной
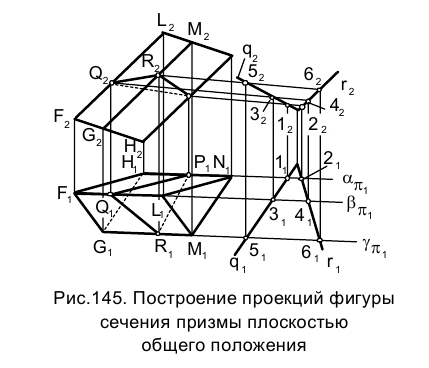
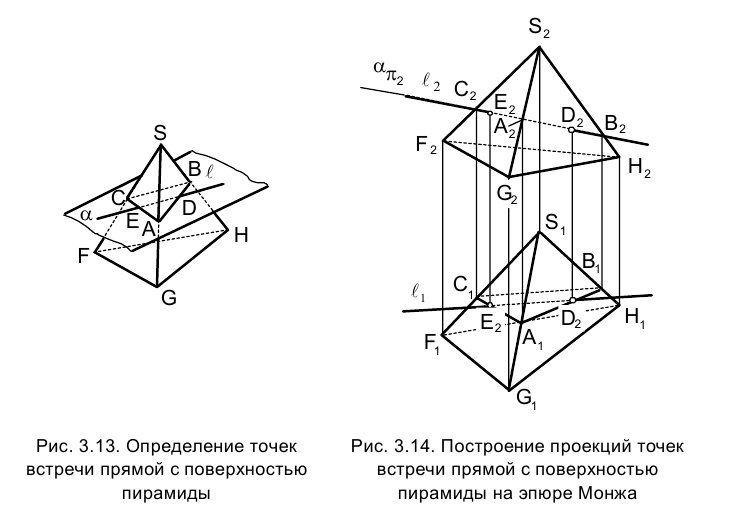
прямой со сторонами построенного много угольника. Положения, изложенные выше, иллюстрируются примером построения точек встречи прямой ℓ с поверхностью трехгранной пирамиды SFQH в пространстве (рис. 3.13) и их проекций на эпюре Монжа (рис. 3.14).

В качестве вспомогательной плоскости используется содержащая прямую ℓ фронтально проецирующая плоскость 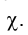Фигурой, получающейся в пересечении плоскости с поверхностью пирамиды, является треугольник АВС, а Е и D - точки пересечения прямой ℓ с его
сторонами AB и АС соответственно.

Построение разверток многогранников

Разверткой многогранной поверхности называется плоская фигура, составленная из граней поверхности, совмещенных с некоторой плоскостью последовательным их вращением относительно ребер.

Все грани многогранной поверхности изображаются на развертке в натуральную величину, и, следовательно, ее построение сводится к определению истинных величин отдельных граней поверхности.
Последовательность расположения граней на развертке может быть самой различной и определяться оптимальным использованием площади формата, на котором вычерчивается развертка.

Рассмотрим несколько характерных примеров:

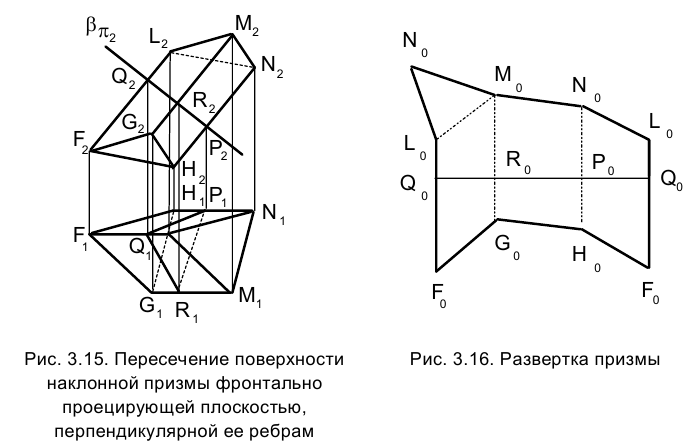
1. Построим развертку наклонной призмы FGНLМN (рис. 3.15), боковые ребра которой являются фронталями. Пересечем призму фронтально проецирующей плоскостью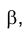, перпендикулярной ее боковым ребрам, и построим проекции треугольника сечения QRР. Одним из известных способов определим истинные величины сторон треугольника QRР и построим отрезок 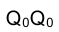(рис. 3.16), равный его периметру, который можно рассматривать как развертку нормального сечения призмы - треугольника QRР. В точках 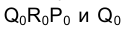по направлениям, перпендикулярным к 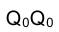, откладываем по обе стороны длины отрезков боковых ребер, снимая их с фронтальной проекции призмы. Соединив концы отложенных отрезков ребер прямыми линиями, получим фигуру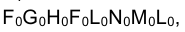, представляющую собой развертку боковых граней призмы. Остается построить основание призмы, что не вызывает затруднения.

2. Если на одной из плоскостей проекций основание призмы проецируется в истинную величину, ее развертку можно построить более простым способом. Представим себе, что фронтальная плоскость проекции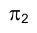проходит через ребро 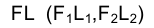(рис. 3.17).

Совместим все боковые грани призмы с плоскостью 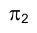Отбросим основания призмы, сделаем разрез ее боковой поверхности по ребру FL и повернем грань FLGМ вокруг ребра FL до положения, параллельного плоскости . Траекториями движения вершин треугольников основания в пространства являются окружности, центры которых лежат на ребре призмы.

На эпюре Монжа фронтальные проекции вершин треугольников оснований будут в процессе вращения грани в пространстве перемещаться по прямым, перпендикулярным фронтальной проекции ребра FL.

Грань FLGМ изобразится на эпюре Монжа в истинную величину тогда, когда в истинную величину изобразится на плоскости сторона FG треугольника основания. Смещенные положения точек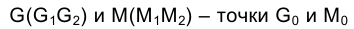 соответственно. Положение точки 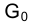определяется на прямой 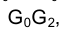, перпендикулярной к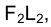, как результат ее пересечения с другой окружностью радиуса 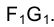. Точка М0 определяется в результате пересечения прямых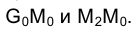

Аналогично вышесказанному далее выполняется поворот грани GМНМ относительно ребра GL и грани HNFL относительно ребра HN. Соединив соответствующие точки прямыми и достроив ее основания, построим развертку призмы.

Первый способ построения развертки призмы называется способом нормального сечения, второй - способом раскатки.

3. Построение развертки пирамиды (рис. 3.18) сводится к построению истинных величин ее граней, которыми являются треугольники. Для этого следует любым из известных способов построить истинные величины ее ребер, а уже затем построить и истинные величины граней.

• Заказать чертежи

Многогранники. Точка и прямая на поверхности

Гранные поверхности имеют прямую образующую и ломаную линию в качестве направляющей.

У пирамидальной поверхности образующая 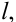 двигаясь по ломаной направляющей а, все время проходит через одну точку S, называемую вершиной.  

Образующая призматической поверхности, двигаясь в пространстве по ломаной направляющей, все время остается параллельной самой себе.

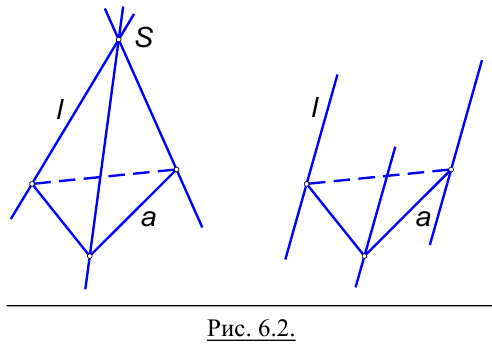
Многогранник – пространственная фигура, ограниченная со всех сторон плоскостями (гранями).

Построение проекций точек, принадлежащих боковой поверхности многогранника осуществляется с помощью образующих и направляющей.

Возьмем трехгранную пирамиду и точки D,E, F, лежащие на ее боковой поверхности. Необходимо определить недостающие горизонталь+ные проекции этих точек:

1. Точки E и F лежат на ребрах пирамиды, следовательно, их горизонтальные проекции будут лежать на горизонтальных проекциях соответствующих ребер.
2. Точка D принадлежит грани пирамиды, поэтому ее недостающую проекцию следует определять с помощью образующей 1-S. Кроме того, из графического условия не ясно, на какой грани находится точка D, ее фронтальной проекции  соответствуют две горизонтальные проекции.

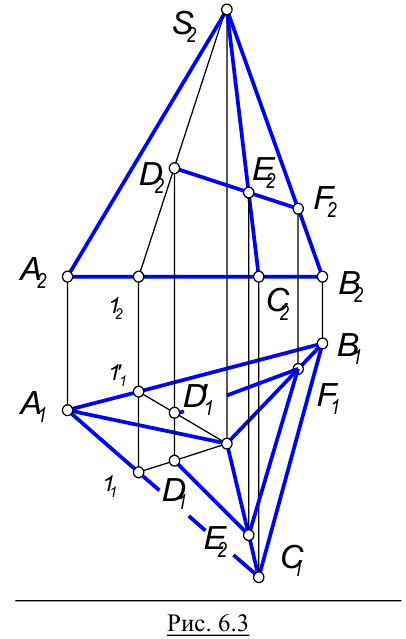
Из КЧ видно, что прямая или ломаная линия, принадлежащая поверхности многогранника может быть построена по характерным точкам, которыми являются точки перехода ее через ребра.

Поверхности вращения

Поверхности вращения имеют произвольную образующую, движущуюся по окружности.

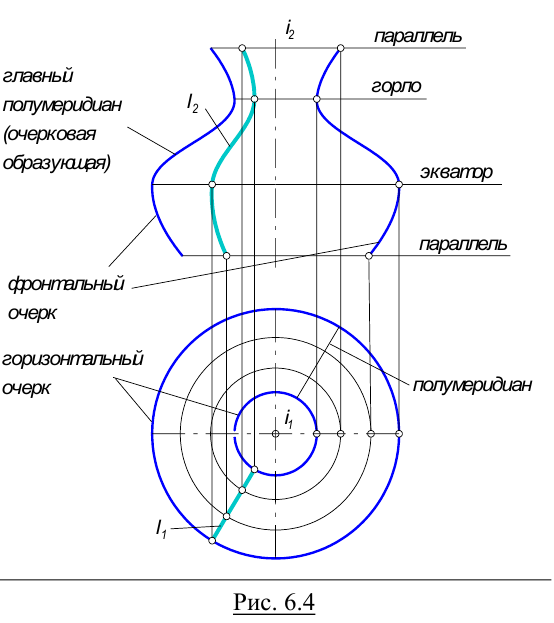
Каждая точка образующей 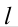 движется по окружности с центром на оси вращения  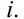Это окружность называется параллелью. Параллель, проходящая через наиболее удаленную от оси вращения точку образующей, называется экватором, а через ближайшую – горлом.  

Линия m, получаемая при пересечении поверхности плоскостью, проходящей через ось вращения, называется меридианом. Все меридианы поверхности вращения конгруэнтны. Каждый из них разделяется на два симметричных относительно оси вращения полумеридиана. Меридиан, лежащий в плоскости, параллельной плоскости проекций называется главным меридианом.  В данном примере он определяет фронтальный очерк поверхности, горизонтальный очерк определяется экватором и горлом.

Цилиндр вращения

Цилиндрическая поверхность вращения – поверхность, образованная движением прямой линии вокруг оси.

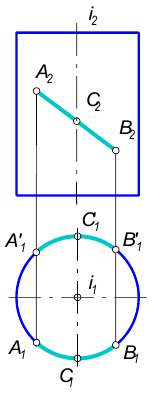
Возьмем фронтально-проецирующий цилиндр и линию АВ, расположенную на его боковой поверхности. Горизонтальная проекция этой линии спроецируется на горизонтальный очерк цилиндра, т.к. все ее точки лежат на его боковой поверхности.

Линия принадлежит поверхности, если каждая ее  точка принадлежит этой поверхности.

Конус вращения

Коническая поверхность вращения образуется движением прямой линии, пересекающей ось вращения.

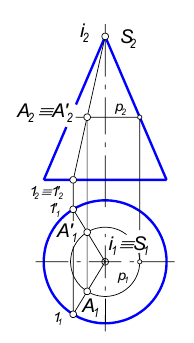
Точка принадлежит поверхности, если она принадлежит линии, лежащей на этой поверхности.

Построение точек, принадлежащих поверхности вращения, ведется с помощью образующих или параллелей поверхности.

Пусть задана фронтальная проекция точки А, принадлежащей поверхности конуса. Этой проекции соответствуют две горизонтальные проекции точки 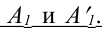 Их можно определить с помощью образующих поверхности  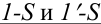или параллели p.

Пересечение прямой с поверхностью

Возможны три варианта расположения прямой относительно поверхности. Прямая может:

• - пересекать поверхность;
• - касаться поверхности;
• - не пересекать  поверхность.

Частные случаи:

1. Пересекаются прямая общего положения 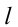  с проецируюей поверхностью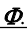

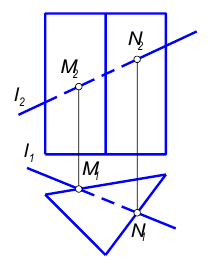
Рис. 6.10       

Если задана проецирующая поверхность, то одна из проекций искомых точек пересечения определяется сразу, исходя из принадлежности их этой проецирующей поверхности.

В данном примере призма является горизонтально- проецирующей поверхностью, следовательно, горизонтальные проекции точек пересечения лежат на пересечении горизонтальной проекции прямой 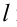 и очерка призмы.

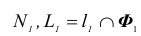
Вторая проекция точек определяется исходя из принадлежности их непроецирующей прямой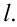

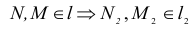
2. Пересекаются проецирующая прямая i с поверхностью конуса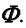

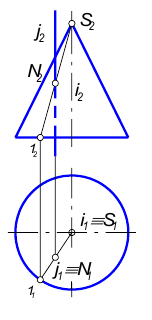
Рис. 6.11

В этом случае одна из проекций искомой точки  также изначально определена на чертеже.   Она совпадает с вырожденной проекцией прямой.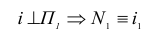

Вторая проекция точки определяется из условия принадлежности ее образующей поверхности.

Общий случай:  

Пересекаются непроецирующая поверхность и прямая общего положения.

В этом случае, чтобы найти точки пересечения прямой с поверхностью необходимо:

1. Заключить прямую в дополнительную (вспомогательную) плоскость.
2. Построить линию пересечения вспомогательной плоскости с поверхностью.
3. Определить точки полученного сечения с заданной прямой. Эти точки являются искомыми.

В качестве вспомогательной плоскости выбирают плоскость общего или частного положения, дающую наиболее простую линию сечения (ломаную или окружность).

Пример: Построить точки пересечения прямой 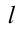 с трехгранной пирамидой SABC. Определить видимость прямой относительно поверхности.

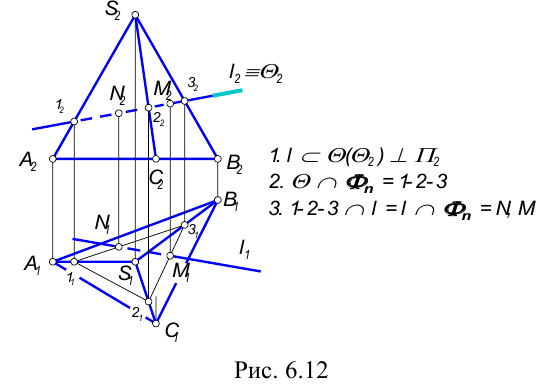
Видимость прямой определяется по принадлежности точек пересечения граням пирамиды. Видима та часть прямой, которая исходит из точки, лежащей на видимой грани многогранника.

Пересечение поверхности многогранника плоскостью

Плоская фигура, получаемая в результате пересечения какой-либо поверхности плоскостью, называется сечением.

Сечением многогранника является многоугольник, его обычно строят с помощью вспомогательных секущих плоскостей. Построение линии пересечения поверхности с плоскостью начинают с нахождения особых (опорных) точек. Для многогранника это точки пересечения ребер и сторон его основания с заданной плоскостью (если построение ведется «способом ребер») или линии пересечения граней и основания многогранника с плоскостью (если построение ведется «способом граней»).

Пример: Построить линию пересечения трехгранной пирамиды SABC плоскостью общего положения 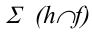 . Построить развертку нижней отсеченной части пирамиды.

Основание  пирамиды принадлежит горизонтальной плоскости проекций, его горизонтальная проекция является натуральной величиной. Плоскость задана таким образом, что пересекает только боковую поверхность пирамиды. Следовательно, сечение будет иметь треугольную форму. Т.к. горизонталь плоскости h проходит через одну из вершин основания, то одна из точек сечения известна – точка C. Остальные точки сечения можно найти с помощью дополнительных секущих плоскостей. Для улучшения наглядности изображения необходимо показать видимость:

1. сечения относительно поверхности многогранника и выделить его цветным карандашом;
2. поверхности относительно заданной плоскости;
3. геометрических элементов, которыми задана плоскость относительно поверхности многогранника.

Натуральную величину сечения определяется вращением вокруг линии уровня, другие необходимые для построения развертки натуральные величины в данной задаче определены методом прямоугольного треугольника.

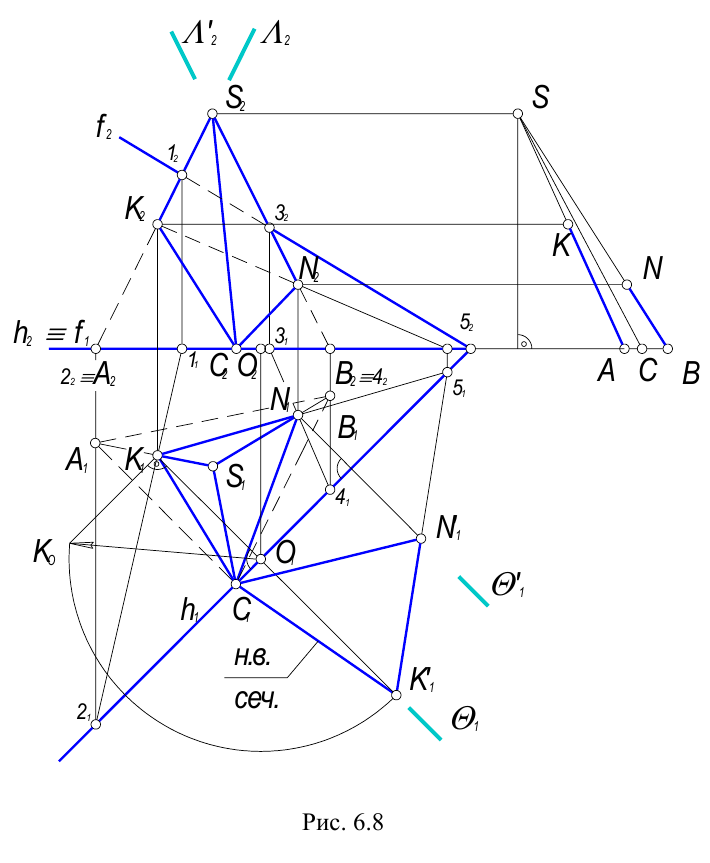
Построение развертки:

1) Методом прямоугольного треугольника находятся длины ребер пирамиды. Т.к. разность высот от концов отрезка до горизонтальной плоскости проекций 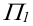 у всех трех ребер одна и равна высоте пирамиды, катет прямоугольного треугольника, равный этой величине, целесообразней начертить в стороне от изображения, правее фронтальной проекции пирамиды. Второй катет равен горизонтальным проекциям ребер. Для определения натуральной величины отрезков AK и BN, необходимо провести горизонтальные вспомогательные линии до пересечения с гипотенузами прямоугольных треугольников.

2) Развертка строится способом треугольников с использованием приема засечек.