Графостатика в теоретической механике

Основы графостатики:

Рассмотрим графический способ сложения сил, приложенных к твердому телу.  

Пусть даны три силы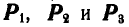

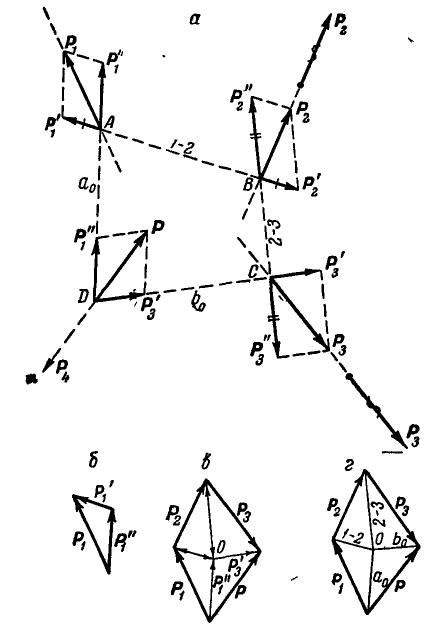
Рис. 68.

Продолжаем далее линию действия 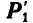до пересечения с линией действия 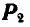и в полученную точку пересечения В переносим 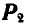. В свою очередь, раскладываем 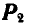на две составляющие 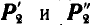, из которых 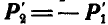, и, наконец, в точке С раскладываем 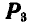на составляющие  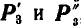, из которых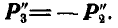

Силы 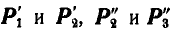попарно уравновешиваются и заданная система сил 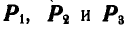привелась к двум силам 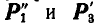, которые при переносе их в точку D дают равнодействующую всех сил Р.

Построение, аналогичное проделанному для одной силы (рис. 68, б), проведем для всех сил (рис. 68, в). Таким образом, произвольно задавшись направлениями составляющих первой силы 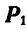 вполне определенную точку О.

Проведем наши рассуждения в обратном порядке. Для заданных сил 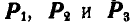построим многоугольник сил (рис. 68, г); замыкающая этого многоугольника Р даст по величине и направлению равнодействующую данных сил. Для нахождения положения линии действия равнодействующей выбираем произвольную точку О (полюс) и соединяем ее с вершинами многоугольника сил прямыми (лучами). Обозначим луч, идущий к началу первой силы, через 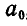, следующие лучи — через 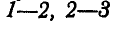и последний через 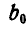. Затем проведем в плоскости действия сил направление 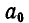до пересечения с первой силой (рис. 68, a) полученной точки А проведем направление 1—2  до пересечения с линией действия второй силы, затем направление 2—3  — до пересечения с линией действия третьей силы и, наконец, направление 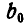. Продолжая 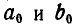(рис. 68, а) до взаимного пересечения, получим точку D, принадлежащую линии действия равнодействующей, в которую и переносим Р с многоугольника сил.

Изложенное построение носит название способа веревочного многоугольника и широко применяется при графических расчетах.   

Ломаная DABCD называется веревочным многоугольником, а участки ломаной DA, АВ, ВС и CD — сторонами веревочного многоугольника.

Задача №1

Даны четыре силы 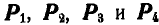, действующие на тело (рис. 69, а). Найти их равнодействующую Р.

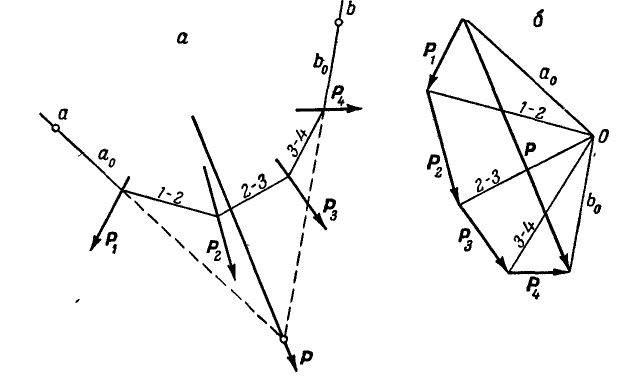
Рис. 69.

Решение. Строим в стороне многоугольник сил (рис. 69, б). Замыкающая этого многоугольника Р и определит величину и направление искомой равнодействующей. Для нахождения положения равнодействующей выбираем на плоскости произвольно полюс О и проводим лучи 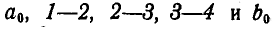. Переносим луч 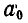параллельно самому себе и продолжаем его до пересечения с линией действия силы 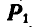(безразлично, в какой точке). Из полученной точки пересечения 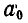с линией действия 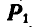проводим, направление, параллельное лучу 1—2 до пересечения с линией действия 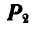и т. д.

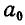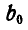Продолжая крайние стороны веревочного многоугольника и (рис. 69, а) до пересечения, получим точку, принадлежащую линии действия равнодействующей сил, куда и переносим параллельно самой себе Р с многоугольника сил.

Если бы мы в точках а и b закрепили нить и приложили к ней данные нам силы 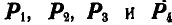, то форма, которую примет нить, будет соответствовать форме построенного нами веревочного многоугольника.

При построении веревочного многоугольника могут встретиться следующие случаи.

Первый случай. Если бы (рис. 68,а) нам были заданы не три силы, а четыре, из которых четвертая сила 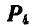равна и направлена в обратную сторону найденной равнодействующей сил Р, то заданные четыре силы находились бы в равновесии; с этом случае и многоугольник сил (рис. 68, в) и веревочный многоугольник ABCDA (рис. 68, а) были бы замкнуты.

Итак, силы, приложенные к твердому телу, взаимно уравновешиваются, если многоугольник сил и веревочный многоугольник замкнуты.

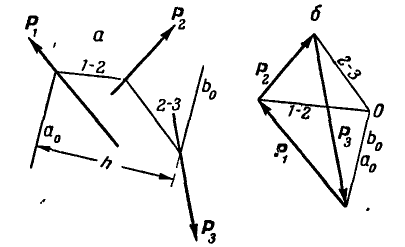
Рис. 70.

• Заказать решение задач по теоретической механике

Второй случай. Может оказаться, что многоугольник сил (рис. 70, б) будет замкнут, а веревочный многоугольник не будет замкнут (рис. 70, а), так как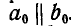 . В этом случае силы приводятся к паре с плечом h.

Отсюда следует, что силы, приложенные к твердому телу, приводятся к паре, если многоугольник сил замкнут, а веревочный многоугольник не замкнут.

Третий случай. Если многоугольник сил не замкнут, то силы, приложенные к твердому телу, всегда приводятся к одной равнодействующей (рис. 68, а).

Не трудно видеть, что равенство нулю главного вектора соответствует замкнутости многоугольника сил, а равенство нулю главного момента — замкнутости веревочного многоугольника.

Задача №2

Определить графически опорные реакции опор А и В для следующих случаев.

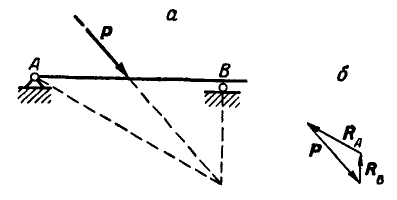
Рис. 71.

При действии на балку одной силы Р (рис. 71, а).

Решение. Здесь мы имеем случай действия на балку трех сил — заданной силы Р и двух реактивных сил шарниров А и В, а так как балка находится в равновесии, то эти силы должны пересекаться в одной точке. Найдя точку пересечения линий действия сил 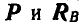, соединим эту точку с шарниром А и тем самым найдем направление линии действия 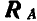.  На рисунке 71, б дано построение треугольника равновесия, из которого в выбранном нами при построении масштабе находятся .

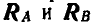При действии на балку двух сил 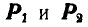(рис. 72, а).

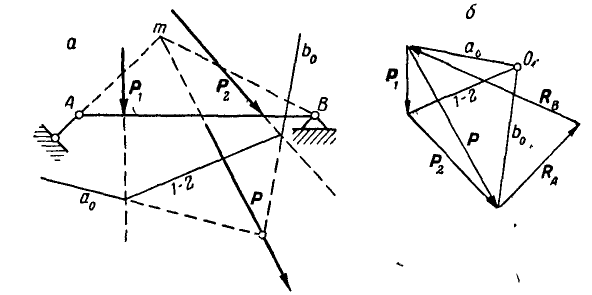
Рис. 72.

Решение. Находим сначала по правилу веревочного многоугольника (рис. 72, а) равнодействующую Р заданных сил .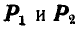

Теперь на данную балку действуют уже три силы 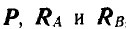, которые должны пересекаться в одной точке 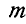; реакции  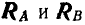находятся так же, как и в предыдущей задаче (рис. 72, б).

При действии на ферму любых сил 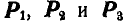 (рис. 73, а).

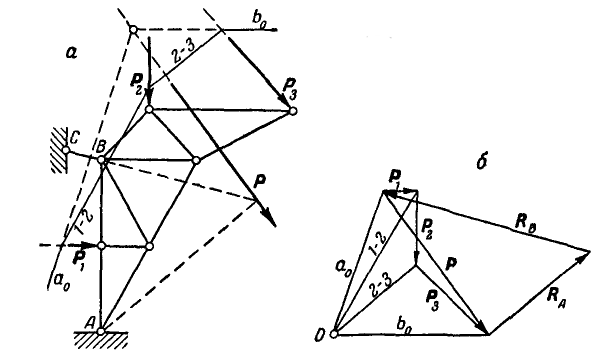
Рис. 73.

Решение. Найдя по правилу веревочного многоугольника (рис. 73, а) равнодействующую Р всех заданных сил 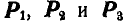, строим затем треугольник равновесия для трех сил 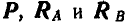, действующих на ферму (рис. 73, б).

Если точка пересечения линий действия трех сил — равнодействующей заданных сил Р и реакций 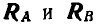— получается за пределами чертежа, то изложенный метод практически неудобен. В этом случае для нахождения неизвестных реакций 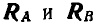следует воспользоваться условием замкнутости веревочного и силового многоугольников, не прибегая к предварительному нахождению равнодействующей Р заданных сил 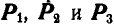. С этой целью строим сначала, как и в предыдущем случае, многоугольник заданных сил 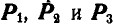и из произвольной точки О (рис. 74, б) проводим лучи.

При построении веревочного многоугольника (рис. 74, а) первую сторону 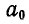обязательно проводим через неподвижный шарнир А, направление реакции которого нам не известно. Затем продолжаем построение веревочного многоугольника так же, как и в предыдущем случае. Так как веревочный многоугольник должен быть замкнут, то на основании этого проводим его замыкающую, для чего следует соединить точки пересечения 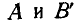крайних сторон веревочного многоугольника 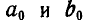с линиями действия опорных реакций .

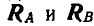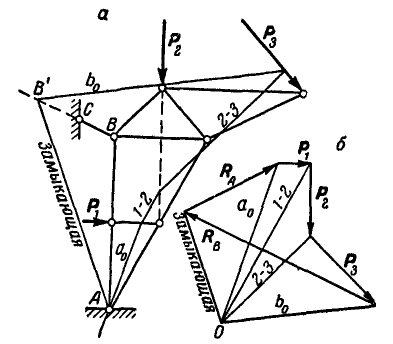
Рис. 74.

Одна из таких точек А на чертеже имеется; другая точка В' определится, если направления ВС и стороны 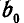веревочного многоугольника продолжить до взаимного пересечения в точке 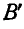(рис. 74, а).

Проводим затем из полюса О (рис. 74, б) линию, параллельную замыкающей, а из конца силы 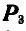направление, параллельное ВС  — линии действия реакции в точке В до пересечения с замыкающей, и полученную точку пересечения соединяем с началом силы тем самым мы замыкаем многоугольник сил.

Чтобы убедиться в правильности построения многоугольника сил, замечаем, что каждая из сил на чертеже (рис. 74, а) проходит через соответствующую вершину веревочного многоугольника; на многоугольнике же сил (рис. 74, б) каждая сила должна быть расположена между лучами, обозначенными так же, как и стороны веревочного многоугольника, образующие вершину, через которую проходит соответствующая сила. Например, сила А проходит через вершину веревочного многоугольника, образованную сторонами 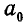и 1—2; на многоугольнике же сил она расположена между лучами 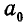и 1—2.

Аналогично реакция шарнира В проходит через вершину веревочного многоугольника, образованную сторонами 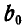 и замыкающей; на многоугольнике сил реакция 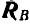находится между лучами 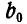и замыкающей и т. д.

Задача №3

Определить графически реакции шарниров А и В при действии на балку параллельных сил 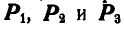(рис. 75, а).

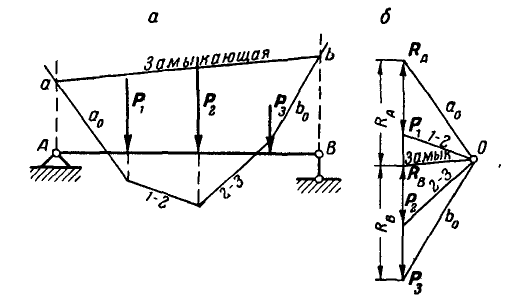
Рис. 75.

Решение. Строим для данных сил 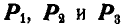веревочный многоугольник со сторонами 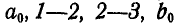. Так как балка АВ под действием заданных и реактивных сил находится в равновесии, то многоугольник сил и веревочный многоугольник должны быть замкнуты. На основании этого проводим на веревочном многоугольнике замыкающую, соединив точки а и b пересечения крайних сторон веревочного многоугольника 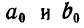с линиями действия опорных реакций.

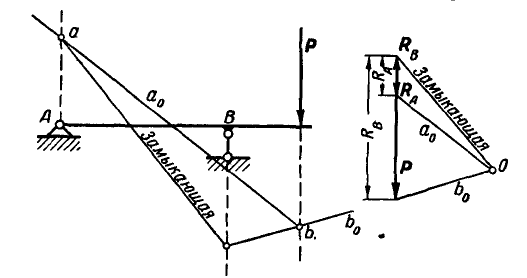
Рис. 76.

Проводим затем из полюса О линию, параллельную замыкающей; эта линия на многоугольнике сил отсечет отрезки, выражающие в масштабе 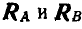. Для того чтобы узнать, какой же из полученных отрезков выражает 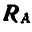или 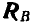, заа0мечаем, что на рисунке 75, а сила 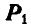лежит на пересечении сторон 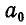и 1—2, на рисунке же 75, б она лежит между 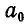и 1—2. Точно так же на рисунке 75, а реакция  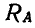находится на пересечении сторон 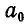и замыкающей, поэтому на рисунке 75, б она тоже должна находиться между  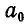и замыкающей, в чем мы убеждаемся.

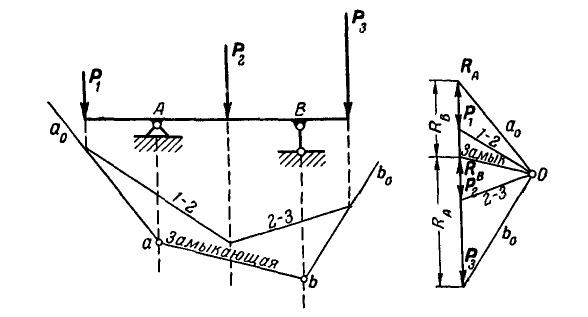
Рис. 77.

Замкнутый многоугольник всех параллельных сил, действующих на балку, 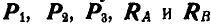, как в нашем случае, обращается в прямую (рис. 75, б).

Аналогично предыдущей задаче находят опорные реакци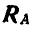и и 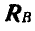консольных балок (рис. 76 и 77) и консольной балки, нагруженной равномерно распределенной нагрузкой (рис. 78).

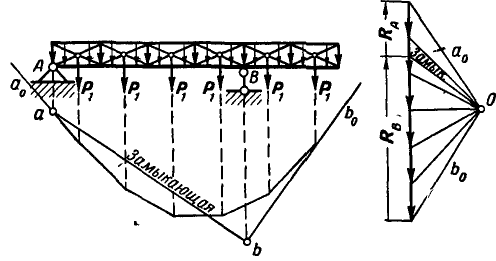
Рис. 78.

В том случае, когда на балку действует сплошная равномерная нагрузка, на сравнительно небольших (равных, а иногда и неравных) участках балки заменяем сплошную нагрузку сосредоточенными силами и проводим построение так же, как и для случая действия на балку параллельных сил (рис. 78). Чем на меньшее число участков мы разобьем балку, тем точнее получится результат. В пределе при бесконечно большом числе участков бесконечно малой длины веревочный многоугольник выразится в виде плавной кривой.