Гипербола - определение и вычисление с примерами решения

Гипербола:

Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек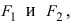

Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы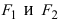

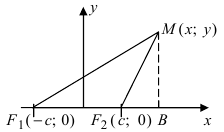
Рис. 31. Вывод уравнения гиперболы.

Расстояние между фокусами (фокусное расстояние) равно 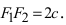Согласно определению, для гиперболы имеем 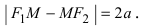Из треугольников 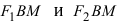по теореме Пифагора найдем 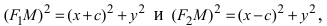соответственно.

Следовательно, согласно определению имеем

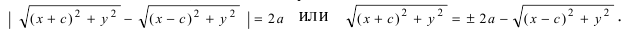
Возведем обе части равенства в квадрат, получим

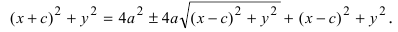
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим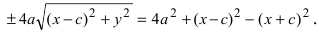 Раскроем разность квадратов 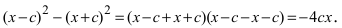Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение 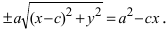Вновь возведем обе части равенства в квадрат 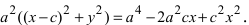Раскрывая все скобки в правой части уравнения, получим 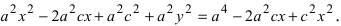Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим 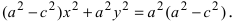Введем обозначение для разности, стоящей в скобках 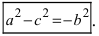Получим 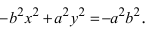Разделив все члены уравнения на величину 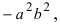получаем каноническое уравнение гиперболы: 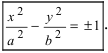Для знака “+” фокусы гиперболы расположены на оси Ох, вдоль которой вытянута гипербола. Для знака фокусы гиперболы расположены на оси Оу, вдоль которой вытянута гипербола.

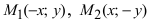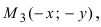Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки и следовательно, гипербола симметрична относительно координатных осей, которые в данном случае будут называться осями симметрии гиперболы (Рис. 32). Найдем координаты точек пересечения гиперболы с координатными осями: 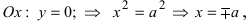т.е. точками пересечения гиперболы с осью абсцисс будут точки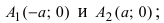 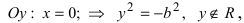т.е. гипербола не пересекает ось ординат.

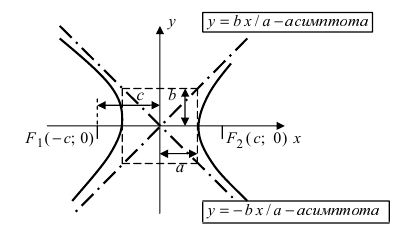
Рис. 32. Асимптоты и параметры гиперболы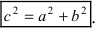

Определение: Найденные точки 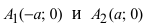называются вершинами гиперболы.

Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 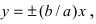не пересекая эти прямые. Из уравнения гиперболы находим, что 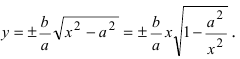При неограниченном росте (убывании) переменной х величина 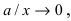следовательно, гипербола будет неограниченно приближаться к прямым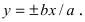

Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.

В данном конкретном случае параметр а называется действительной, а параметр b - мнимой полуосями гиперболы.

Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы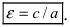

Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 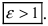Кроме того, эта характеристика описывает форму гиперболы. Для демонстрации этого факта рассмотрим квадрат отношения мнимой полуоси гиперболы к действительной полуоси 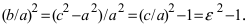Если эксцентриситет 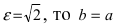и гипербола становится равнобочной. Если 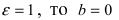и гипербола вырождается в два полубесконечных отрезка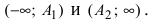

Пример:

Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).

Решение:

Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины: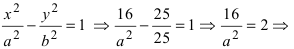

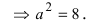Следовательно, каноническое уравнение гиперболы имеет вид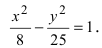

Пример:

Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы - в вершинах эллипса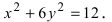

Решение:

Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 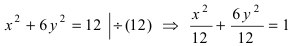или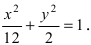 Следовательно, большая полуось эллипса 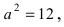а малая полуось 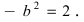Итак, вершины эллипса расположены на ос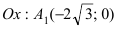и и 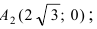на оси 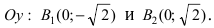Так как 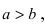то эллипс вытянут вдоль оси абсцисс Ох. Определим расположение фокусов данного эллипса 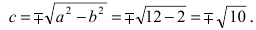Итак, 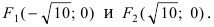Согласно условию задачи (см. Рис. 33):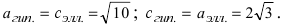

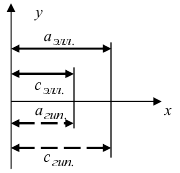
Рис. 33. Параметры эллипса и гиперболы

Вычислим длину мнимой полуоси 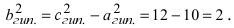Уравнение гиперболы имеет вид: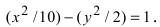

Гипербола в высшей математике

Рассмотрим уравнение

Решая его относительно 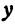, получим две явные функции

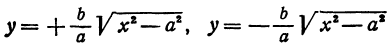
или одну двузначную функцию

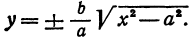
Функция 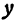имеет действительные значения только в том случае, если . При 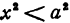функция 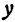действительных значений не имеет. Следовательно, если 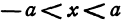, то точек с координатами, удовлетворяющими уравнению (3), не существует.

При 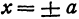получаем.

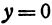При 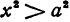каждому значению 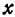соответствуют два значения 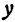, поэтому кривая симметрична относительно оси 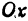. Так же можно убедиться в симметрии относительно оси . Поэтому в рассуждениях можно ограничиться рассмотрением только первой четверти. В этой четверти при увеличении х значение у будет также увеличиваться (рис. 36).

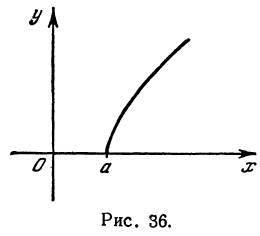
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.

Гипербола в силу симметрии имеет вид, указанный на рис. 37.

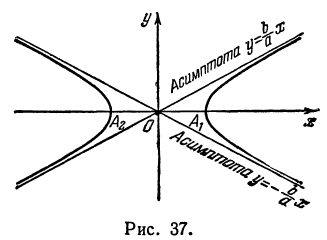
Точки пересечения гиперболы с осью называются вершинами гиперболы; на рис. 37 они обозначены буквам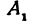и и .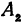

Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.

Рассмотрим прямую, заданную уравнением 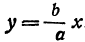. Чтобы не смешивать ординату точки, расположенной на этой прямой, с ординатой точки, расположенной на гиперболе, будем обозначать ординату точки на прямой 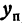, а ординату точки на гиперболе через 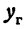. Тогда 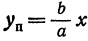, 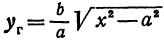(рассматриваем только кусок правой ветви, расположенной в первой четверти). Найдем разность ординат точек, взятых на прямой и на гиперболе при одинаковых абсциссах:

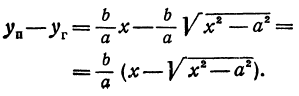
Умножим и разделим правую часть на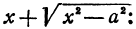

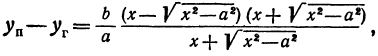
или

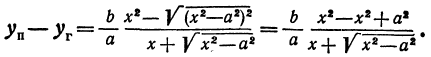
Окончательно

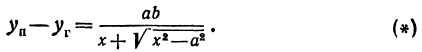
Будем придавать 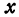все большие и большие значения, тогда правая часть равенства 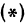будет становиться все меньше и меньше, приближаясь к нулю. Следовательно, разность будет приближаться к нулю, а это значит, что точки, расположенные на прямой и гиперболе, будут сближаться. Таким образом, можно сказать, что рассматриваемая часть правой ветви гиперболы по мере удаления от начала координат приближается к прямой .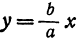

Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 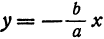. Также кусок левой ветви, расположенный во второй четверти, приближается к прямой 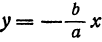, а кусок левой ветви, расположенный в третьей четверти, — к прямой .

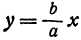Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.

Таким образом, гипербола имеет две асимптоты, определяемые уравнениями (рис. 37).