Геометрическое черчение - примеры с решением заданий и выполнением чертежей

Важность геометрического черчения в различных областях производства и строительства очень велика. По чертежам изготавливаются и собираются детали для машин, механизмов и приборов. Чертежи используются для изготовления строительных конструкций, и на строительных площадках для возведения зданий и различных инженерных сооружений.

Чертеж является одним из главных носителей технической информации, необходимой для разработки, изготовления и контроля. Прочитать или создать чертеж можно лишь в том случае, если известны приемы и правила его составления. Конструкторскую документацию во всех отраслях производства разрабатывают и оформляют по взаимосвязанным правилам и положениям, установленным в стандартах Единой системы конструкторской документации.

Чтобы овладеть навыками составления графической КД (чертежей), необходимо, во-первых, обладать знаниями по начертательной геометрии и, во-вторых, умениями в области черчения.

Геометрическое черчение как дисциплина состоит из следующих разделов:

• геометрическое черчение;
• проекционное черчение;
• машиностроительное черчение.

Задачи геометрического черчения, как предмета изучения, следующие:

• ознакомление с правилами выполнения, оформления чертежей; составления проектной и рабочей конструкторской документации;
• обучение выполнению различных геометрических построений и проекционных изображений как с помощью чертежных инструментов, так и «от руки» (эскизы и технические рисунки);
• изучение условностей и условных графических обозначений, применяемых на чертежах и схемах;

Содержание:

Введение в геометрическое черчение

Значение чертежей в различных областях производства и строительства очень велико. По чертежам изготавливают детали различных механизмов, машин и аппаратов и осуществляют их сборку. Пользуясь чертежами, производят строительные конструкции на домостроительных комбинатах, а затем на строительных площадках выполняют монтаж зданий и возводят различные инженерные сооружения.

История развития черчения как способа изображения уходит в далекое прошлое. Сначала появились изображения различных предметов – рисунки. Позднее при строительстве жилищ, крепостей и других сооружений появились чертежи, которые назывались планами. Первоначально изображение в плане (вид сверху) совмещали с изображением фасада здания (вид спереди). Неудобство такого совмещения заставило разъединить оба вида и применить два, три и более видов.

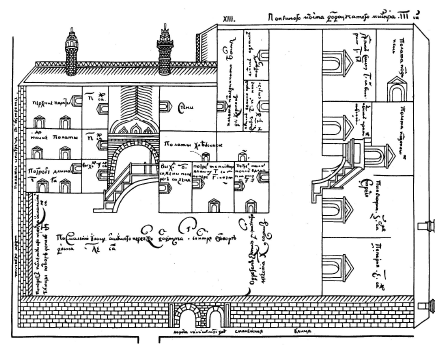
К XVIII в. относится развитие русской горнорудной промышленности, строительства речных и морских судов, заводских силовых установок и машин. В этот период разрабатывались достаточно сложные чертежи, в связи с чем по указу Петра I было введено преподавание черчения в специальных технических школах и в горнозаводских училищах на Урале, готовивших мастеров и техников горного дела.

В архивах сохранился чертеж двадцатидвухвесельного шлюпа, выполненный лично Петром I в 1719 году. Чертеж составлен с соблюдением проекционной связи и с применением наложенных сечений.

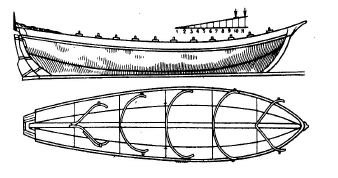
С развитием машинной техники наблюдается дальнейшее совершенствование способов изображений. Чертежи многочисленных русских строителей и изобретателей приближаются по своему виду к современным чертежам. Таков, например, чертеж молотовой фабрики Ф. Санникова, относящийся к 1741 г.

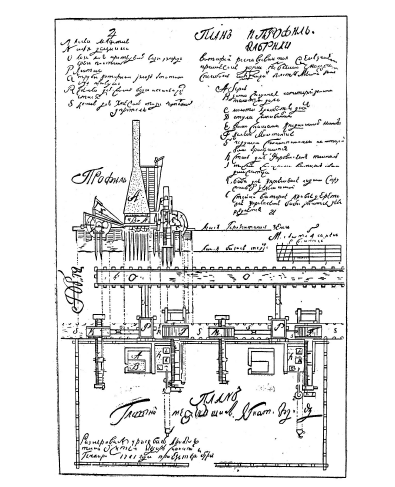
С развитием техники чертежи усложнялись, и их выполнение требовало более высокой точности исполнения. Стали применять масштабы, проекционную связь, выполняя разрезы, без которых невозможно было понять внутреннее устройство изделия и принцип его работы. Эти чертежи были уже близки к современным чертежам, но на них не было размеров. Размеры определялись с помощью масштабной шкалы, изображенной на поле чертежа.

И.И. Ползунов, построивший в 1763 г. первую в мире паровую машину, предназначенную для привода в действие заводских установок, разработал для её изготовления чертежи. На чертежах изображены поперечный разрез машины (рис. а), на котором показаны применяемые материалы (кирпич, древесина, грунт), отдельные детали (рис. б), что является прообразом современного деталировочного чертежа.

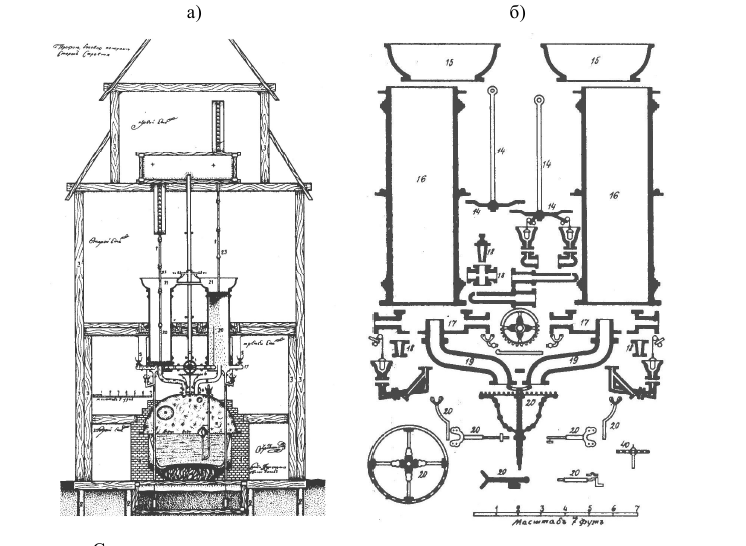
Сохранились чертежи многочисленных сложных механизмов и станков, выполненных изобретателем-механиком И.П. Кулибиным (1735 – 1818 гг.). Чертежи И.И. Ползунова и И.П. Кулибина наглядно показывают отличные познания русских изобретателей в области построения точного проекционного чертежа изделия. Чертеж подъемного ворота иллюстрирует технику выполнения чертежей в конце XVIII в.

Автор чертежа подъемного ворота «машинный ученик» Ф. Борзов впоследствии стал видным теплотехником, строителем первых паровых машин в России. Этот чертеж выполнен по методу ортогональных проекций в 1793 году, т.е. за несколько лет до опубликования Г. Монжем работы «Начертательная геометрия».

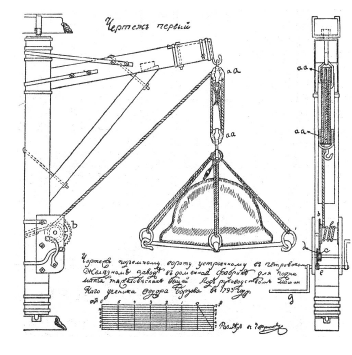
В 1799 г. французский ученый и инженер Гаспар Монж опубликовал труд «Начертательная геометрия». Отдавая должное Г. Монжу, обобщившему метод прямоугольного проецирования предметов на две взаимно перпендикулярные плоскости проекций, мы не должны забывать, что задолго до появления начертательной геометрии в отдельных русских чертежах были поставлены и решались те же задачи, которые научно обобщил Г. Монж.

Продолжателями дела И.И. Ползунова в развитии техники и совершенствовании чертежа были русские механики отец и сын Черепановы. В 1824 году по их чертежам была построена первая паровая машина, разработан паровоз.

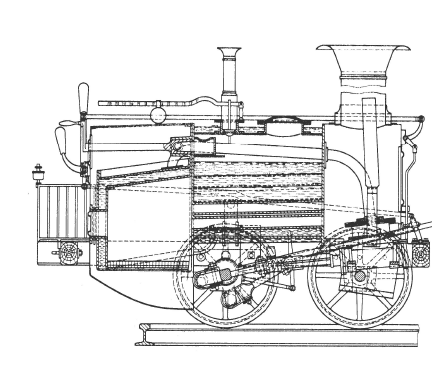
Архитектурно-строительные чертежи, выполненные талантливыми русскими зодчими, отличались высоким графическим совершенством и содержали планы, фасады и разрезы зданий, построенные в точном соответствии с законами прямоугольного проецирования. Архитектор В.И. Баженов (1737 – 1799 гг.) и его ученик М.Ф. Казаков (1738 – 1812 гг.) оставили большое количество памятников – архитектурных ансамблей и дворцов, до сих пор украшающих улицы Москвы.

К началу XIX века была разработана и оформилась наука – начертательная геометрия, получившая широкое применение при решении задач строительной техники, фортификационных сооружений и в дальнейшем при выполнении машиностроительных чертежей. Основоположником начертательной геометрии в России был проф. Я.А. Севастьянов, издавший в 1821 г. свой курс «Основания начертательной геометрии». Крупнейшие ученые В.И. Курдюмов (1853 – 1904 гг.), Н.А. Рынин (1877 – 1942 гг.), А.И. Добряков (1895 – 1947 гг.), Д.И. Каргин (1880 – 1947 гг.) заложили основы русской графической науки и способствовали научными исследованиями ее развитию. Во второй половине ХХ века советскими учеными

Н.А. Поповым, С.М. Колотовым, Н.Ф. Четверухиным, И.И. Котовым и др. были созданы научные основы проекционных методов изображений. В настоящее время без чертежей и других конструкторских документов не возможно изготовление изделий ни в одной области производства или строительства. Выпуск любого изделия производства начинается с разработки конструкторской документации (КД), используемой для определения состава и устройства изделия и содержащей все необходимые данные для его изготовления, контроля, приемки, эксплуатации и ремонта.

К проектной и рабочей КД относятся графические и текстовые документы. Основным требованием при разработке и изготовлении КД является единообразие и правильное оформление чертежей, а также текстовых документов, что облегчает их выполнение и чтение. Это требование распространяется на документы, оформленные как вручную, так и в любом графическом редакторе (AutoCAD, КОМПАС, SolidWorks и др.). Чтобы овладеть навыками составления графической КД (чертежей), необходимо, во-первых, обладать знаниями по начертательной геометрии и, во-вторых, умениями в области черчения.

Черчение как дисциплина состоит из следующих разделов:

• – геометрическое черчение;
• – проекционное черчение;
• – машиностроительное черчение.

Задачи черчения, как предмета изучения, следующие:

• – ознакомление с правилами выполнения, оформления чертежей; составления проектной и рабочей конструкторской документации;
• – обучение выполнению различных геометрических построений и проекционных изображений как с помощью чертежных инструментов, так и «от руки» (эскизы и технические рисунки);
• – изучение условностей и условных графических обозначений, применяемых на чертежах и схемах;
• – приобретение необходимых навыков в чтении чертежей различного назначения.

Раздел «Геометрическое черчение» направлен на изучение и графическое закрепление следующих тем:

• – правила оформления чертежей;
• – выполнение геометрических построений на чертежах;
• – выполнение изображений и надписей на чертежах.

Советы студентам по геометрическому черчению

Черчение – трудоемкий предмет. Хотя в курсе черчения нет сложных формул, трудных теорем, научиться чертить нелегко. Предмет требует от изучающего усидчивости, точности, опрятности. Поэтому необходимо так организовать свою работу по черчению, чтобы при наименьшей затрате времени выполнять задания по учебному графику. Хорошо продуманные подготовительные операции в значительной мере предопределяют успех изучения курса. Необходимо предварительно обдумать содержание чертежа, затем правильно расположить соответствующие изображения и данные на поле чертежа, выявить неясные места, разъяснения на которые следует получить у преподавателя или прочитать в учебнике. При таком методе работы чертежи получаются качественными, студенты приобретают навыки правильной организации труда, которые впоследствии при выполнении курсовых и дипломных работ и проектов, а также при работе на производстве окажутся весьма ценными.

Никогда не чертите то, что вам непонятно. Это приводит к непроизводительной трате времени, к некачественной работе и возможной переделке чертежей. Старайтесь пройти все этапы выполнения чертежа самостоятельно, пользуясь консультациями преподавателя. Это позволит закрепить изучаемый материал и использовать его в дальнейшем при обучении на последующих курсах. И последнее, позднее вы будете использовать графические редакторы для облегчения оформления чертежей, но помните, продумать содержание любого чертежа, как конструкторского документа, может только человек.

Государственные стандарты геометрического черчения

В современных условиях разработки и применения проектной и рабочей конструкторской документации (чертежей, схем и текстовых документов) одним из основных требований является единый подход к оформлению КД, позволяющий облегчить процесс ее выполнения и чтения. Для выполнения этого требования следует руководствоваться правилами, установленными государственными стандартами (ГОСТ).

Система государственных стандартов

Во всех странах мира огромное внимание уделяют развитию стандартизации.

Стандартизация – важное средство ускорения научнотехнического прогресса. Она позволяет экономить трудовые и материальные ресурсы, сокращать сроки проектирования и изготовления изделий, повышать качество промышленной и сельскохозяйственной продукции, снижать ее стоимость. Объектами стандартизации являются конкретная продукция, методы ее производства и контроля, термины, определения и другие нормы и правила, многократно применяемые в науке, технике, промышленном и сельскохозяйственном производстве, строительстве, транспорте и других сферах народного хозяйства.

Стандарт (от англ. standard – норма, образец) в широком смысле слова – эталон (образец, модель), принимаемый за исходный для сопоставления с ним других подобных объектов. Стандарт в Российской Федерации – документ, устанавливающий комплекс норм, правил, требований к объекту стандартизации, в котором в целях добровольного многократного использования устанавливаются характеристики продукции, правила осуществления и характеристики процессов производства, эксплуатации, хранения, перевозки, реализации и утилизации, выполнения работ или оказания услуг.

Межгосударственные стандарты (ГОСТ) принимает Межгосударственный Совет по стандартизации, метрологии и сертификации. Национальные стандарты (ГОСТ Р) принимает Государственный комитет РФ по стандартизации.

Из истории обозначения государственных стандартов

Первые государственные стандарты в России вышли в 1926 году. К аббревиатуре ОСТ (общесоюзный стандарт) добавлялся порядковый номер стандарта. С 1938 года к обозначению стандарта стали добавлять через «–» последние две цифры года его регистрации. С 1940 года взамен ОСТов стали выпускать ГОСТы (Государственные стандарты), которым стали присваивать порядковые номера, начиная с единицы: ГОСТ 1–40, ГОСТ 2–40 и т. д.

В 1968 году стали выпускать комплексы (системы) межотраслевых стандартов, содержащие взаимоувязанные правила и положения. Стандарты, входящие в такие системы, не включены в общую нумерацию. Каждой системе присвоен цифровой порядковый индекс. В утвержденные стандарты могут вноситься изменения. На первой странице такого стандарта в сноске указывают номер изменения, номер и год издания ежемесячного информационного указателя стандартов (ИУС), в котором оно опубликовано. Тогда в конце обозначения стандарта в ряде случаев проставляется:

• – * (означает, что в стандарт внесены изменения);
• – ** (означает, что стандарт заменен или отменен в частях);
• – *** (означает, что стандарт ранее отменен, но позднее восстановлен).

В 1992 году была введена Межгосударственная система стандартизации (ГОСТ 1.0–92 «Межгосударственная система стандартизации. Основные положения») и

Государственная система стандартизации Р Ф (ГОСТ Р 1.0–92 «Государственная система стандартизации. Основные положения»).

Цели и принципы стандартизации в РФ установлены Федеральным законом от 27 декабря 2002 года «О техническом регулировании» (Глава 3. Стандартизация), а правила применения национальных стандартов РФ – ГОСТ Р 1.0–2004 «Стандартизация в РФ. Основные положения».

Обозначение межгосударственных стандартов установлено ГОСТ 1.5–2001 «Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Общие требования к построению, изложению, оформлению, содержанию и обозначению»; национальных – ГОСТ Р 1.5–2004 «Стандартизация в РФ. Стандарты национальные РФ. Правила построения, изложения, оформления и обозначения».

Все сведения об обозначении стандартов и их изменении содержатся в Указателе «Межгосударственные стандарты» и Указателе «Национальные стандарты» , которые публикуются каждый год с данными, как правило, на 1 января текущего года. Указатель «Национальные стандарты. 2011» опубликован Федеральным агентством по техническому регулированию и метрологии по состоянию на 1 января 2011 года.

Обозначение государственных стандартов

Государственные стандарты могут иметь сквозную нумерацию и могут входить в систему (комплекс) стандартов. Комплексы (системы) стандартов содержат взаимоувязанные правила и положения, относящиеся преимущественно к организации и управлению производством, техникоэкономической и другой документации. Система построения обозначений государственных стандартов и национальных стандартов показана на рис. 1 и рис. 2.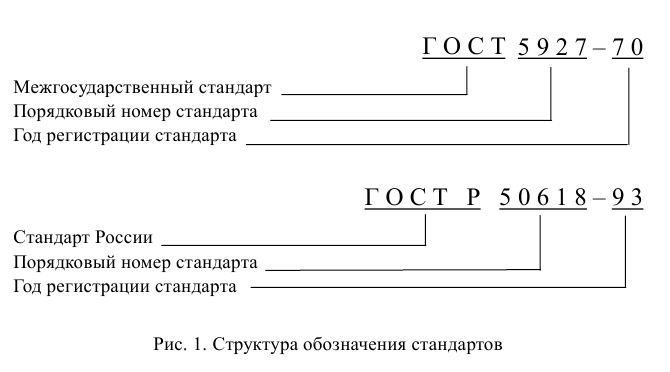

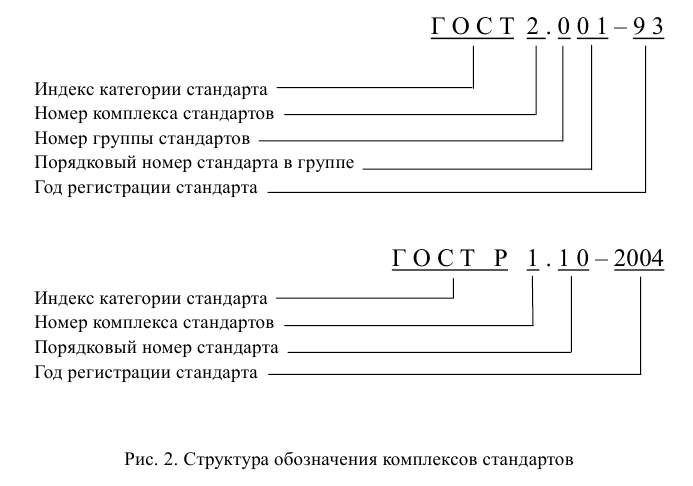
В настоящее время действует несколько систем (комплексов) межгосударственных и национальных стандартов. Некоторые из них представлены в табл. 1.

Система стандартизации в Российской Федерации определяется законом «О техническом регулировании» (Глава 3. Стандартизация) от 27 декабря 2002 года и национальными стандартами (ГОСТ Р) (табл. 2). В них даны определения понятий «стандартизация» и «стандарт»; установлены категории стандартов, объекты стандартизации; регламентированы стадии разработки, порядок внедрения; изложены основные положения о контроле за внедрением и соблюдением стандартов, о порядке их пересмотра, о построении, изложении и оформлении стандартов.

Системы государственных стандартов

Таблица 1

Индекс категории стандарта	Номер комплекса стандартов (класса)	Наименование комплекса		Пример обозначения стандарта в комплексе
ГОСТ Р	1	Стандартизация в Российской Федерации		ГОСТ Р 1.0–2004
ГОСТ	1	Межгосударственная система стандартизации	МСС	ГОСТ 1.2–2009
ГОСТ	2	Единая система конструкторской документации	ЕСКД	ГОСТ 2.001–93
ГОСТ	3	Единая система технологической документации	ЕСТД	ГОСТ 3.1001–81
ГОСТ	4	Система показателей качества продукции	СПКП	ГОСТ 4. 200–78
ГОСТ	6	Унифицированные системы документации	УСД	ГОСТ 6.10.1–88
ГОСТ	7	Система стандартов по информации, библиотечному и издательскому делу		ГОСТ 7.32–2001
ГОСТ	8	Государственная система обеспечения единства измерений	ГСИ	ГОСТ 8.383–80
ГОСТ	14	Единая система технологической подготовки производства	ЕСТПП	ГОСТ 14.004–83
ГОСТ	19	Единая система программной документации	ЕСПД	ГОСТ 19.001–77
ГОСТ	21	Система проектной документации для строительства	СПДС	ГОСТ 21.001–77

Классификационные группы стандартов ГОСТ Р

Таблица2

Обозначение стандарта	Наименование
ГОСТ Р 1.0–2004	Стандартизация в РФ. Основные положения
ГОСТ Р 1.2–2004	Стандартизация в РФ. Стандарты национальные РФ. Правила разработки, утверждения, обновления и отмены
ГОСТ Р 1.4–2004	Стандартизация в РФ. Стандарты организаций. Общие положения
ГОСТ Р 1.5–2004	Стандартизация в РФ. Правила построения, изложения, оформления и обозначения стандартов
ГОСТ Р 1.8–2004	Стандарты межгосударственные. Правила проведения в РФ работ по разработке, применению, обновлению и прекращению применения
ГОСТ Р 1.9–2004	Стандартизация в РФ. Знак соответствия национальным стандартам РФ
ГОСТ Р 1.10–2004	Стандартизация в РФ. Правила стандартизации и рекомендации по стандартизации. Порядок разработки, утверждения, изменения, пересмотра и отмены

Назначение и область распространения стандартов ЕСКД

Единая система конструкторской документации (ЕСКД) – комплекс межгосударственных стандартов, определяющих правила и положения по разработке, оформлению и обращению конструкторской документации. Основное назначение стандартов ЕСКД – установление в организациях и на предприятиях единых правил выполнения, оформления и обращения конструкторской документации (КД). Система построения обозначения стандартов ЕСКД показана на рис. 3.

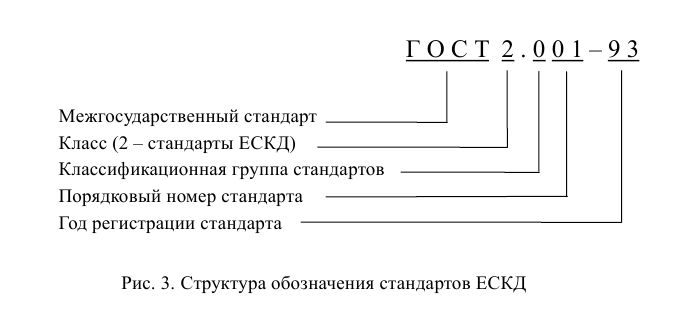
Правила и положения ЕСКД распространяются на все виды КД, учетно-регистрационную и нормативно-техническую документацию, техническую, научно-техническую и технологическую документацию.

Состав и классификация стандартов ЕСКД

Стандарты ЕСКД объединены в класс 2 (табл. 3). В пределах этого класса стандарты распределены по 10 классификационным группам (от 0 до 9). В каждую группу можно внести 99 стандартов, поэтому группы стандартов ЕСКД могут пополняться без нарушения их нумерации.

Классификационные группы стандартов ЕСКД

Таблица 3

Группа	Содержание стандартов	Номера стандартов ГОСТ
0	Общие положения	2.001–93 и последующие
1	Основные положения	2.101–68 и последующие
2	Классификация и обозначение изделий в КД	2.201–80
3	Общие правила выполнения чертежей	2.301–68 и последующие
4	Правила выполнения чертежей изделий машино- и приборостроения	2.401–68 и последующие
5	Правила обращения КД, учет, хранение, дублирование, внесение изменений	2.501–88 и последующие
6	Правила выполнения эксплуатационной и ремонтной документации	2.601–2006 и последующие
7	Правила выполнения схем	2.701–2008 и последующие
8	Правила выполнения документов строительных и судостроительных	2.801–74 и последующие
9	Прочие стандарты

Общие правила выполнения и оформления чертежей

Целью выполнения графической работы №1 «Геометрическое черчение» по инженерной графике является приобретение навыков геометрических построений с соблюдением стандартов, определяющих требования к разработке и оформлению КД. Для достижения этой цели необходима детальная проработка третьей группы стандартов ЕСКД.

Форматы

Форматы листов чертежей и других документов установлены ГОСТ 2.301–68. Форматы листов определяются размерами внешней рамки, выполняемой тонкой сплошной линией. Различают основные (табл. 4) и дополнительные форматы.

Размеры основных форматов

Таблица 4

Обозначение формата	А0	А1	А2	А3	А4
Размеры сторон формата, мм	1189×841	594×841	594×420	297×420	297×210

Формат А0 с размерами сторон 1189×841 мм имеет площадь, равную 1м (рис. 4). Основные форматы (А1; А2; А3; А4) образуются путем последовательного деления листа формата А0 на две равные части, параллельно меньшей стороне. Допускается при необходимости применять формат А5 (148×210 мм).

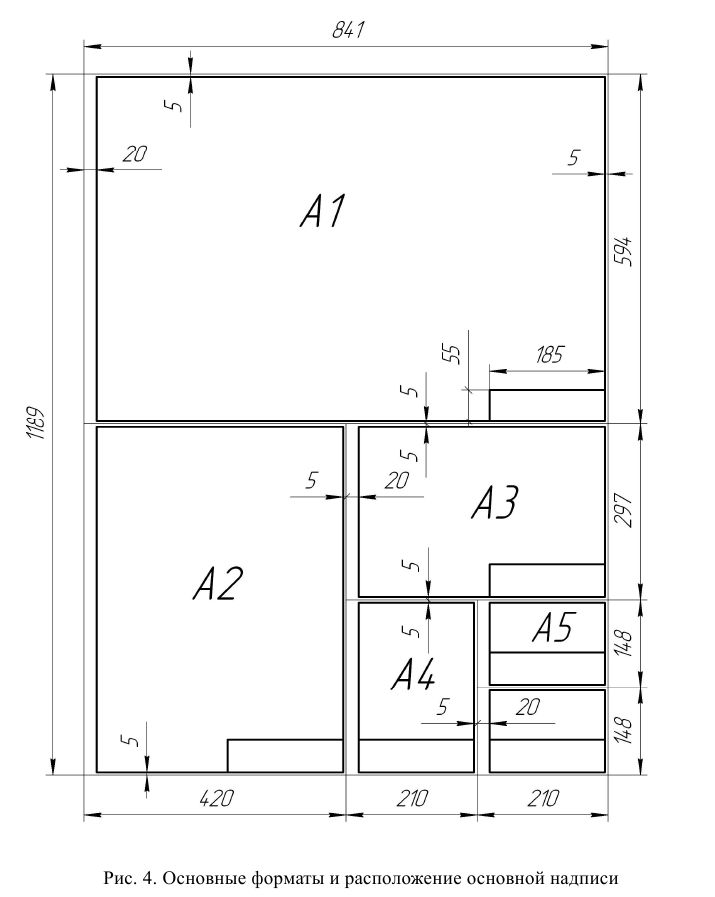
Дополнительные форматы образуются увеличением коротких сторон листов основных форматов в «n» раз, где «n» – целое число. Пример обозначения дополнительного формата: А3×3 (размеры 420×891, где n = 3, 297×3 = 891).

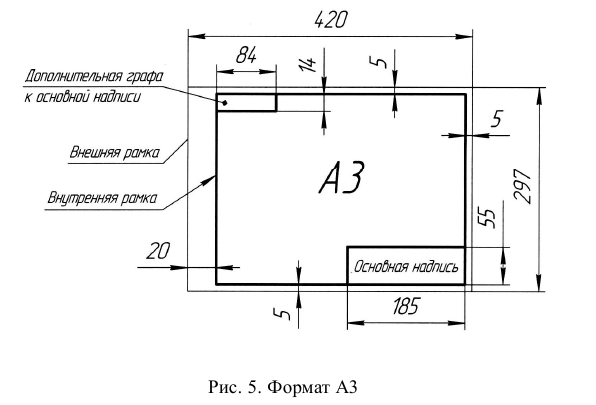
Внешняя рамка (граница формата), определяющая размеры формата, называется линией обреза формата (рис. 5) . В прямоугольнике, ограниченном внешней рамкой, выполняется внутренняя рамка чертежа. Ширина поля для подшивки 20 мм, остальных полей 5 мм. На формате А4 поле для подшивки располагается только вдоль длинной стороны, на остальных (больших) форматах – как вдоль длинной, так и вдоль короткой стороны, в зависимости от расположения изображений.

Прямоугольник, ограничивающий основную надпись, располагается в нижнем правом углу чертежа. На формате А4 основная надпись располагается только вдоль короткой стороны. Расположение основной надписи, в которой содержатся все сведения об изделии и конструкторском документе, приведено на рис. 4, 5.

Основные надписи

Форма, размеры и порядок заполнения основной надписи и дополнительных граф в конструкторских документах установлены ГОСТ 2.104–2006. Основная надпись располагается в правом нижнем углу формата. На формате А4 основная надпись располагается только вдоль короткой стороны (рис. 4). Содержание, расположение и размеры граф основной надписи на чертежах и схемах должны соответствовать форме 1 (рис. 6, табл. 5).

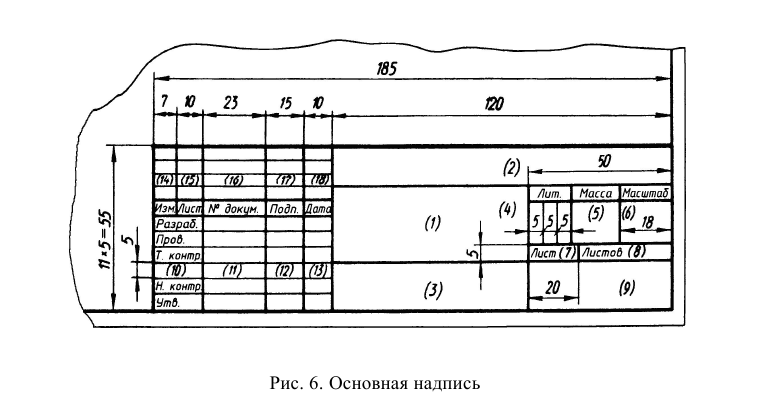
Содержание граф основной надписи

Таблица 5

№ графы	Что указывают в графе	Пример заполнения
1	2	3
1	Наименование изделия (или название работы на учебном чертеже)	Корпус Кран пробковый Геометрическое черчение
2	Обозначение документа	ТПЖА.731110.001
3	Обозначение материала детали (на эскизах допускается указывать упрощенно, без ссылки на стандарт)	Бронза БрА7 ГОСТ 18175-78
4	Литеру, присвоенную данному документу (на учебных чертежах и эскизах графу допускается не заполнять)	А – для чертежей установочной серии; Б – для чертежей серийного или массового производства
5	Массу изделия в килограммах без указания единицы измерения или в других единицах измерения с указанием их	0,42 0,25 т
6	Масштаб	4:1
7	Порядковый номер листа (на документах, состоящих из одного листа, графу не заполняют)	1
8	Общее количество листов документа (графу заполняют только на первом листе)	2
9	Наименование или различительный индекс предприятия, выпускающего документ (если различительный индекс не содержится в обозначении документа)	ВятГУ. Кафедра НГиЧ. Группа ТЭП-12 11-ТЭП-512
10	Характер работы, выполняемой лицом, подписывающим документ	Разраб. Пров. Т. контр. Н. контр. Утв
11	Фамилии лиц, подписавших документ	Иванов
12	Подписи лиц, фамилии которых указаны в графе 11 (подписи лиц, разработавших данный документ и ответственных за нормоконтроль, являются обязательными)
13	Дату подписания документа	02.10.11
14...18	Графы таблицы изменений

Масштабы

Масштабы изображений на чертежах выбирают согласно ГОСТ 2.302–68. Масштабом называется отношение линейных размеров изображаемого на чертеже предмета к его действительным размерам. Масштабы изображений, применяемые для всех отраслей промышленности и строительства, разделяют на три группы (табл. 6)

Масштабы изображений

Таблица 6

Группы масштабов	Масштабы
Масштабы уменьшения	1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000
Натуральная величина	1:1
Масштабы увеличения	2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1

Масштаб, указываемый в соответствующей графе основной надписи чертежа, следует обозначать по типу 1:2; 2:1 и т.д., а в остальных случаях обозначать над изображением по типу: В (2:1) или А–А (4:1).

Линии

Начертания и основные назначения линий на чертежах всех отраслей промышленности установлены ГОСТ 2.303–68. Наименование, начертание, назначение и толщина линий по отношению к толщине основной линии приведены в табл. 7.

Линии чертежа

Таблица 7

Наименование	Начертание	Толщина линии	Основное назначение
1. Сплошная толстая основная		S	Линии видимого контура. Линии контура сечения, вынесенного и входящего в состав разреза
2. Сплошная тонкая			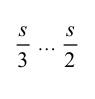Линии размерные и выносные. Линии штриховки. Линии-выноски. Следы плоскостей.
3. Сплошная волнистая			Линии обрыва.
4. Штриховая		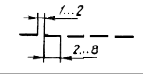	Линии невидимого контура.
5. Штрихпунктирная тонкая		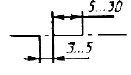	Линии осевые и центровые
6. Сплошная тонкая с изломами		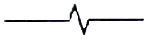	Длинные линии обрыва
7. Штрихпунктирная с двумя точками тонкая		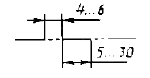	Линии сгиба на развертках
8. Разомкнутая		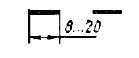s … 1,5s	Линии сечений

Толщина сплошной толстой основной линии s должна быть в пределах 0,5…1,4 мм в зависимости от формата чертежа, величины и сложности изображения. Выбранная толщина линий должна быть одинаковой для всех изображений чертежа. Для учебных чертежей формата А3 толщина s сплошной толстой основной линии принимается 0,8…1,0 мм. Толщину остальных линий принимают в зависимости от выбранной толщины s (0,4…0,5 мм). На формате А3 для построения невидимого контура длину штрихов штриховой линии рекомендуется принимать равной 4…6 мм, промежутки приблизительно равными 2 мм; длину штрихов штрихпунктирной линии, применяемой в качестве осевой и центровой, принимать равной 12…20 мм, а промежутки между ними – 5 мм, включая короткий штрих (≈ 1 мм).

Штрихи в линии должны быть одинаковой длины, промежутки между ними также должны быть равны на всем поле чертежа. Штрихпунктирные линии, применяемые в качестве осевых и центровых, должны пересекаться между собой, а также с другими линиями чертежа и заканчиваться длинными штрихами. Осевые и центровые линии выводятся за контур изображения на 2…5 мм (для формата АЗ – 2…3 мм).

Шрифты чертежные

Чертежные шрифты, применяемые для нанесения надписей на чертежах и других КД, установлены ГОСТ 2.304–81. Чертежный шрифт содержит русский, латинский и греческий алфавиты, арабские и римские цифры, а также знаки. Надписи и размерные числа должны быть выполнены стандартным чертежным шрифтом с наклоном. Угол наклона букв к основанию строки примерно 75°. Заголовки и обозначения в основной надписи допускается выполнять шрифтом без наклона. Различают два типа шрифта: тип А и тип Б. Размер шрифта определяется высотой h прописных (заглавных) букв и цифр в миллиметрах.

Устанавливаются следующие размеры шрифта: 1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.

Типы шрифтов:

• – тип А – толщина линий шрифта d = 1/14 h;
• – тип Б – толщина линий шрифта d = 1/10 h.

Для упрощения выполнения надписей применяется вспомогательная сетка (рис. 7), в которую вписывают буквы, цифры и знаки. Допускается использовать крупную сетку (рис. 8).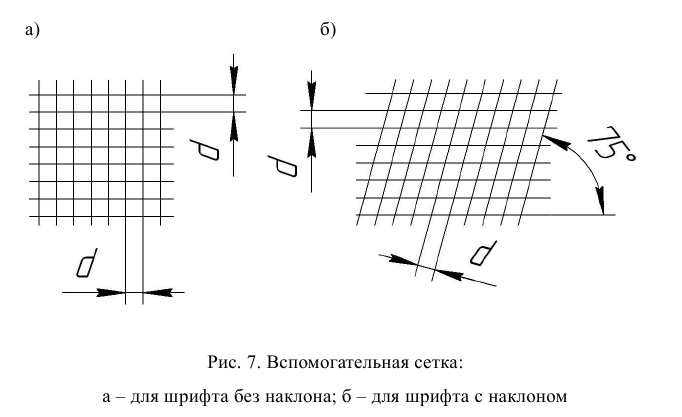

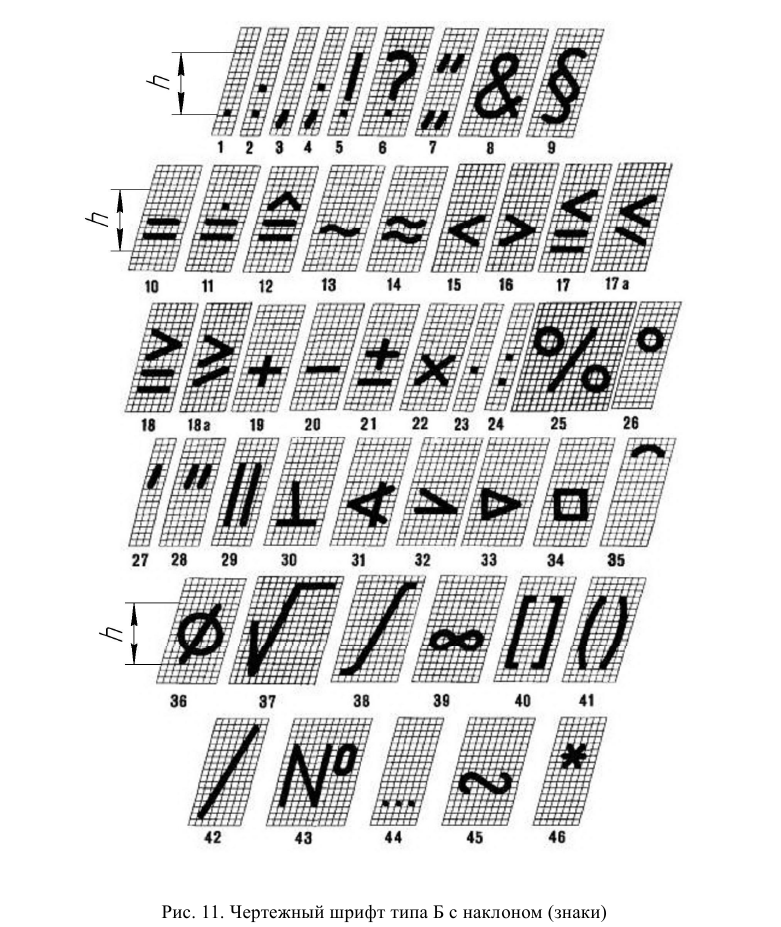
На чертежах, выполненных карандашом, надписи и цифры должны иметь высоту не менее 3,5 мм. Все параметры шрифта типа Б измеряются количеством долей, составляющих 1/10 h, типа А – количеством долей составляющих 1/14 h. Начертание букв, цифр и знаков должно соответствовать рис. 9, 10 и 11 (выдержки из ГОСТ 2.304 – 81).

Соответствующее начертание букв и цифр с использованием крупной сетки приведено на рис. 12.

Пример выполнения надписи чертежным шрифтом типа Б с наклоном приведен на рис. 8.

Основные параметры часто применяемых шрифтов от 3,5 до 10 типа Б с наклоном представлены в табл. 8 и 9.

Таблица 8

Параметры шрифта

Параметры шрифта	Обозначения	Относительный размер	Размеры, мм
			Шрифт
			3,5	5	7	10
Размер шрифта – высота прописных букв и цифр	h	(10/10)h	3,5	5	7	10
Высота строчных букв	c	(7/10)h	2,5	3,5	5	7
Толщина линий шрифта	d	(1/10)h	0,35	0,5	0,7	1,0
Расстояние между буквами	a	(2/10)h	0,7	1,0	1,4	2,0
Минимальное расстояние между словами	l	(6/10)h	не менее ширины букв

Таблица 9

Относительная ширина букв и цифр

Прописные буквы и цифры	И, Й, Л, Н, Т, Ц, Б, В, К, О, Р, У, Ч, Ь, Э, Я, П	(6/10)h
	Г, Е, З, С, 2, 3, 4, 5, 6, 7, 8, 9, 0	(5/10)h
	1	(3/10)h
	А, Д, М, Х, Ы, Ю	(7/10)h
	Ж, Ш, Щ, Ф, Ъ	(8/10)h
Строчные буквы	а, б, в, г, д, и, й, л, о, п, р, с, у, ц, ч, е, з, к, н, х, ъ, ь, э, я	(5/10)h
	ж, т, ф, ш, щ, м, ы, ю	(8/10)h

Обозначения графические материалов и правила их нанесения на чертежах

Графические обозначения материалов в сечениях и правила нанесения их на чертежах приведены в ГОСТ 2.306–68. Общее графическое обозначение материала в сечении независимо от вида материала – равномерная штриховка параллельными сплошными тонкими линиями под углом 45° к рамке чертежа (рис. 13а), к линии контура изображения или к его оси (рис. 13б).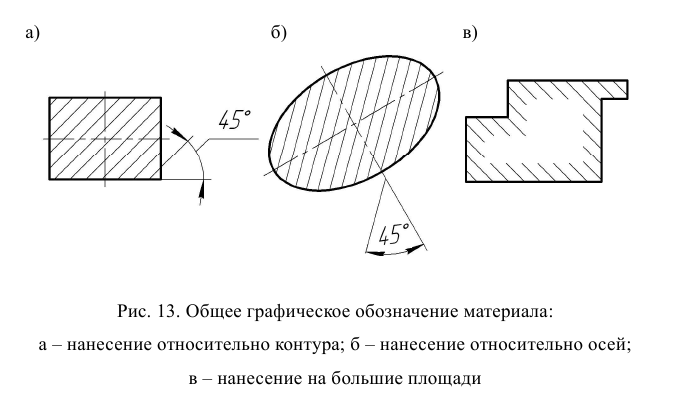

Графическое обозначение материала в сечениях должно передавать информацию о виде материала детали, не затрудняя чтение чертежа. Штриховку металла выполняют тонкими сплошными, параллельными линиями под углом 45° к линии рамки чертежа. Если линии штриховки совпадают с линиями контура или осевыми, то вместо угла 45° штриховку следует выполнять под углами 30° или 60°. Интервал между линиями штриховки должен быть в пределах 1…10 мм. Оптимальный интервал для учебных чертежей 3…5 мм.

Линии штриховки можно наносить с наклоном как в правую, так и в левую стороны, но наклон должен быть одинаковым на всех сечениях одной и той же детали. При больших площадях сечений допустимо наносить обозначение материала лишь у контура сечения полосой равномерной ширины (рис. 13в). Штриховка различных материалов наносится так, как показано в табл. 10.

Таблица 10

Графические обозначения различных материалов

Материал	Обозначение
Металлы и твердые сплавы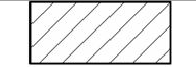
Неметаллические материалы, за исключением указанных ниже
Дерево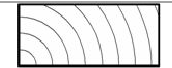
Бетон
Стекло и другие светопрозрачные материалы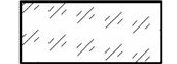
Грунт естественный

Нанесение размеров

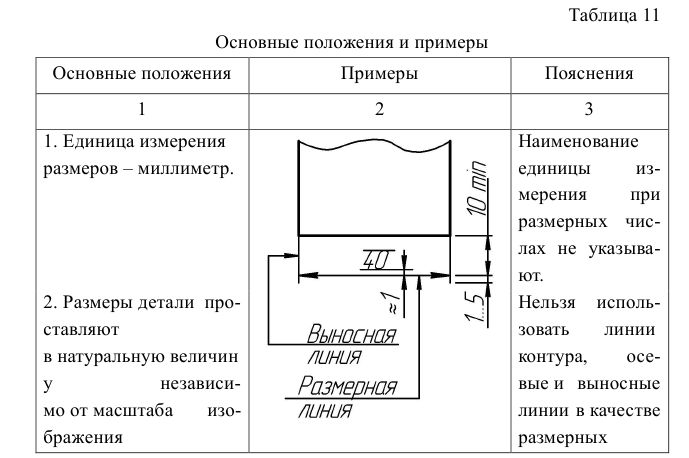
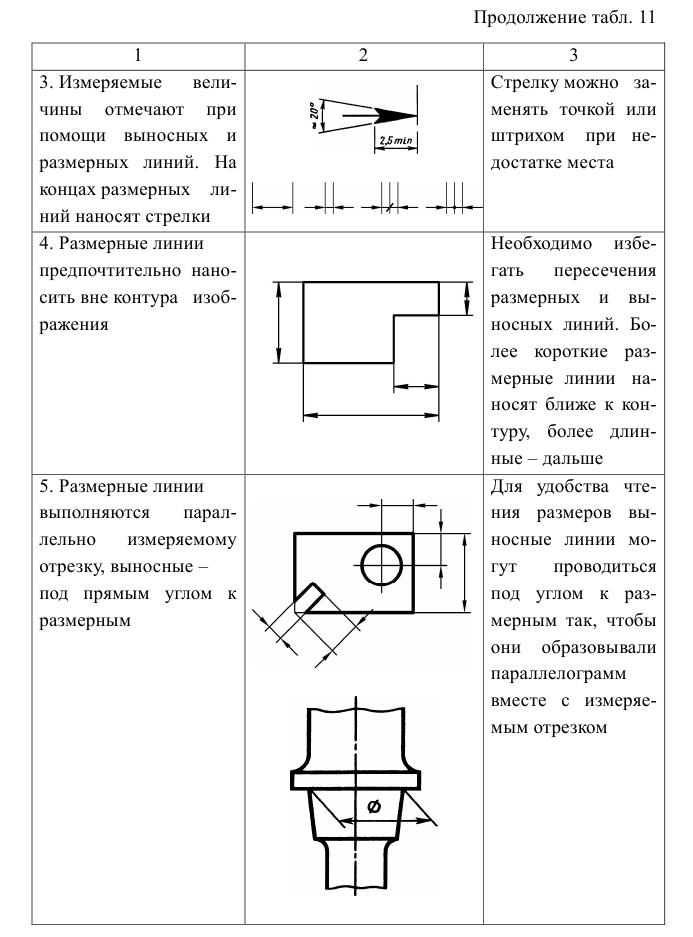
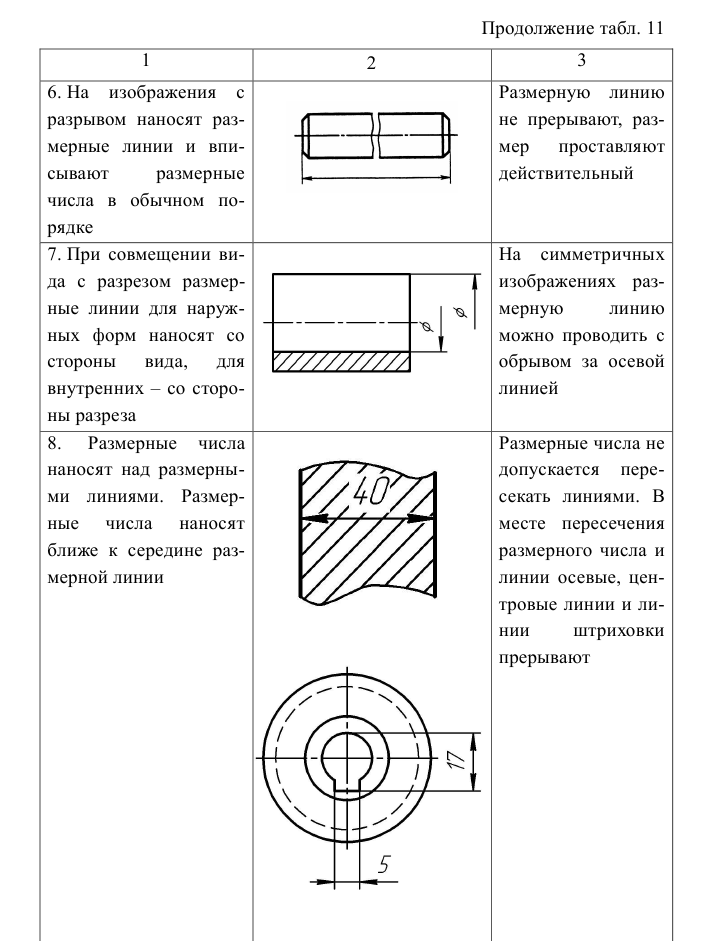
Правила нанесения размеров на чертежах установлены ГОСТ 2.307–68. Величину изображенного изделия и его элементов определяют нанесенные на чертеже размерные числа. Для нанесения размеров используются:

• – выносные линии, проводимые от видимого контура под прямым углом к измеряемому отрезку;
• – размерные линии, проводимые параллельно измеряемому отрезку;
• – размерные числа, располагаемые над размерными линиями или над полками линий-выносок на расстоянии приблизительно 1 мм.

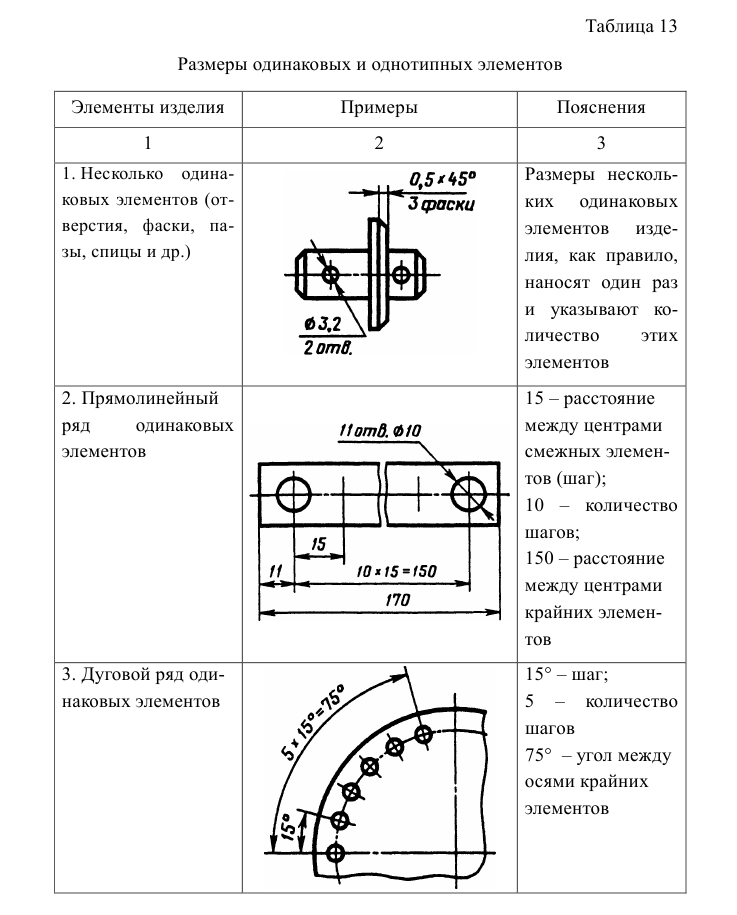
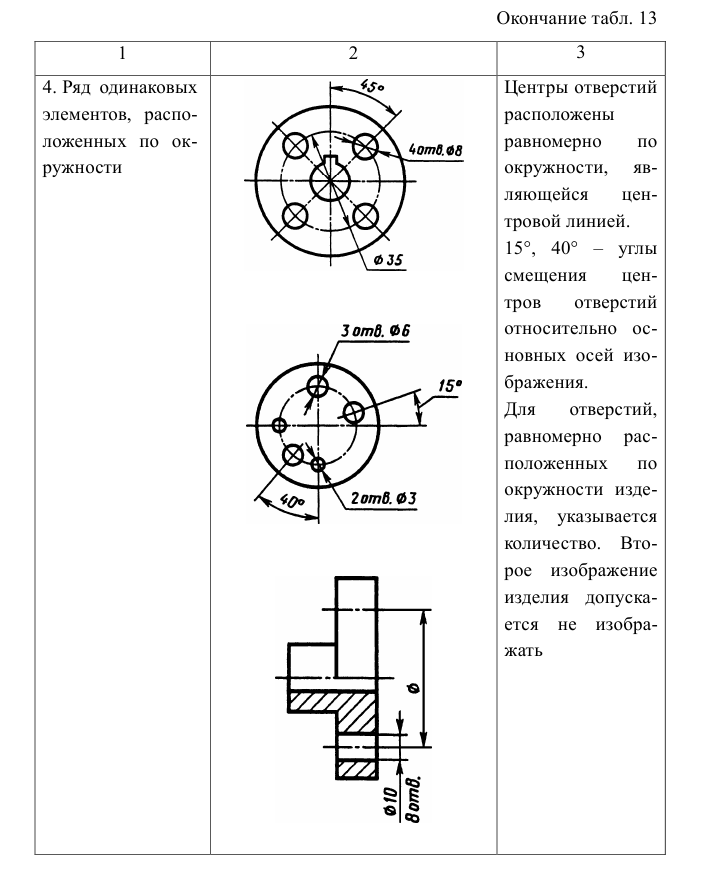
Общее количество размеров на чертеже должно быть минимальным, но достаточным для изготовления и контроля детали. Не допускается повторять размеры одного и того же элемента на разных изображениях.

Порядок выполнения и оформления чертежей

Подготовительный этап

Порядок выполнения и оформления чертежа можно разбить на два этапа: подготовительный и обводка чертежа (табл. 14).

Таблица 14

Порядок выполнения чертежа

№ п/п	Наименование этапа	Параграф в пособии
I этап «Подготовка чертежа»		§ 3.1
1	Организация рабочего места
2	Подготовка чертежных инструментов
3	Выбор и оформление формата
4	Компоновка чертежа
5	Проведение линий чертежа
6	Выполнение изображений
7	Выполнение надписей и нанесение размеров
II этап «Обводка чертежа»		§ 3.2
1	Подготовка чертежа к обводке
2	Подготовка чертежных инструментов
3	Последовательность обводки чертежа
4	Обводка тонких линий
5	Обводка надписей и размерных чисел
6	Обводка линий основного контура и рамки чертежа

Подготовительный этап включает в себя подготовку и проработку чертежа для дальнейшей обводки и сдачи в готовом виде. При подготовке чертежа все построения выполняют в тонких линиях (не нажимая на карандаш). Это позволяет вносить изменения, не ухудшая качества выполняемого чертежа, при удалении ластиком лишних и неправильно проведенных линий.

Организация рабочего места

Для того чтобы качественно выполнить чертеж, необходимо правильно организовать свое рабочее место, правильно подобрать и расположить инструменты. Чертежная доска должна быть изготовлена из мягкой породы дерева (липы). Для установки чертежной доски применяется чертежный стол. Стол должен быть устойчив, доска должна плотно прилегать к столу. Для удобного положения чертежника при работе на столе необходимо иметь приспособление для изменения угла наклона доски. На чертежной доске закрепляют чертежную бумагу.

Свет на чертеж должен падать слева сверху. В этом случае тени от инструментов и от рук не будут мешать работе. При черчении надо сидеть прямо, не горбясь. Расстояние от глаз до чертежа должно быть примерно 300 мм. На чертежной доске оставляют только те инструменты, которые нужны для работы в данное время. При этом готовальня, угольники, карандаши должны лежать справа, а книга слева. От правильной подготовки рабочего места зависит быстрота и аккуратность выполнения чертежа.

Наиболее удобны для выполнения чертежей столы, оборудованные чертежными приборами типа «Кульман». Кульман–высокоточное устройство,обеспечивающее возможность проведения прямых линий заданной длины под любыми углами в плоскости чертёжной доски.

Бумага

Чертежи, как правило, выполняют на плотной чертежной бумаге. Бумага выбирается такая, чтобы с нее хорошо стирались резинкой карандашные линии. Ватман или ватманская бумага (англ. Whatman paper) – белая высокосортная бумага без ярко выраженной фактуры, плотная, с поверхностной проклейкой.

Подготовка чертежных инструментов

Карандаши нужны для построения и обводки чертежей. Они маркируются в зависимости от твердости стержней: Т, 2Т – твердые; М, 2М – мягкие; ТМ – средней твердости. Чем больше число, стоящее на грани карандаша рядом с буквой, тем тверже или мягче этот карандаш. Карандаши импортного производства маркируются буквами Н (твердые) и В (мягкие) с соответствующими числовыми указателями твердости или мягкости; карандаш средней твердости маркируется буквами НВ, F. Студенту необходимо иметь три карандаша: М, ТМ, Т. Карандаши затачивают на длину до 25 мм с конца, противоположного тому, на котором расположена маркировка, графитный стержень должен выступать из деревянной оправки максимум на 6 мм (рис. 14).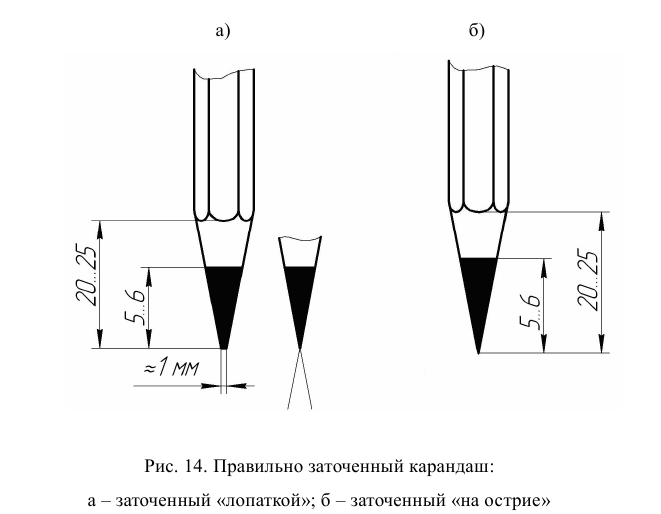

Ластиком удаляют (стирают) линии с чертежа. Он должен быть белым и мягким. При проведении ластиком по листу след от него оставаться не должен, лист повреждаться не должен.

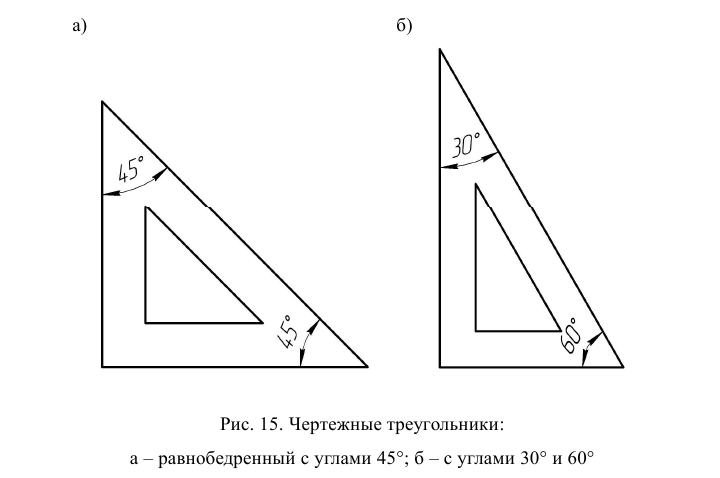
Линейка и треугольник должны быть обязательно деревянными, так как пластмассовые и железные будут загрязнять чертеж. Для работы необходима одна линейка длиной 300 мм и два треугольника (рис. 15).

Чертежный циркуль применяется для вычерчивания окружностей. В одну ножку циркуля (рис.16а) вставляют иглу и закрепляют ее винтом, а в другую – карандашную вставку. Грифель вставки должен быть мягче, чем в используемом карандаше (например, Т и ТМ; ТМ и М; М и 2М). Грифель вставки подготавливают к работе таким же способом, как и для карандаша.

Циркуль - измеритель состоит из двух металлических ножек одинаковой длины с остриями на конце (рис. 16б). Он необходим для измерения отрезков и откладывания заданных расстояний.

Кронциркуль применяется для вычерчивания окружностей малого диаметра (рис. 16в). Вращающаяся ножка для удобства пользования свободно перемещается вдоль оси кронциркуля.

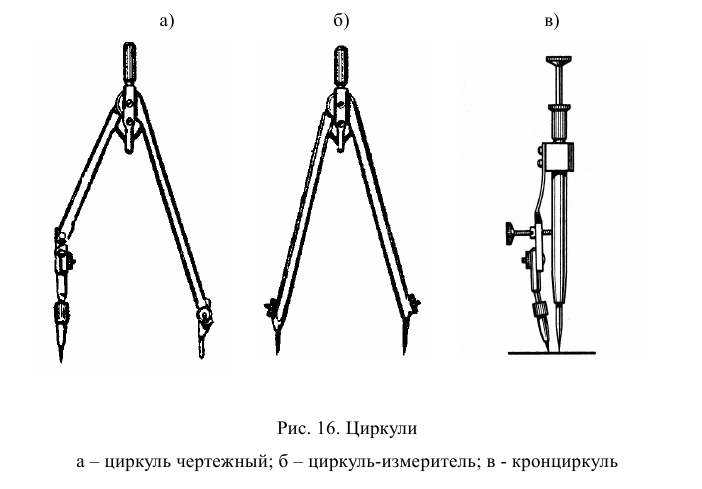
При помощи лекала проводят кривые линии. Контуры лекала образованы дугами разной кривизны (рис. 17).

Выбор и оформление формата

Выбор формата осуществляется в соответствии с ГОСТ 2.301–68 «Форматы». Величина формата зависит от количества и сложности изображений, а также от выбранного масштаба изображений.

Для выполнения ГР «Геометрическое черчение» необходимо использовать формат А3 (420×297), располагать его следует длинной стороной к исполнителю. При построении изображений рекомендуется использовать масштаб изображений 1:1 (в натуральную величину).

При оформлении формата листа необходимо учитывать, что в продаже чаще всего имеются потребительские форматы, т. е. размеры листа немного больше, чем установленные ГОСТ. Такие форматы позволяют закрепить лист на чертежной доске кнопками, не испортив основное поле чертежа. При подготовке формата следует измерить стороны листа. Если они оказались больше стандартных, то это потребительский формат. В таком случае необходимо построить на листе прямоугольник с размерами сторон установленными ГОСТ.

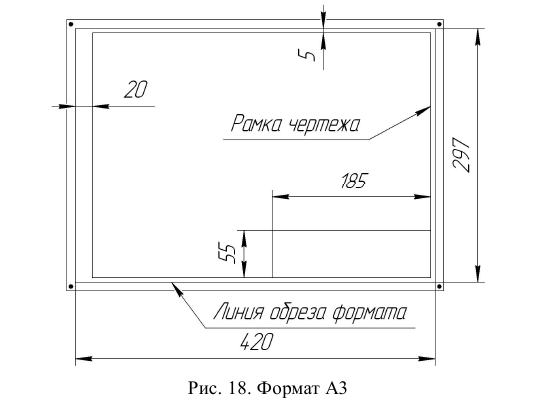
Полученный прямоугольник называют «линией обреза формата», так как после выполнения чертежа формат обрезают по этим линиям. После построения линий обреза формата, выполняют рамку чертежа – прямоугольник, ограничивающий поле чертежа. За рамку чертежа не должны выходить построения и надписи. Рамка чертежа имеет следующий вид (рис. 18): слева от линии обреза формата отступается 20 мм (поле для подшивки), с трех остальных сторон – по 5 мм.

В нижнем правом углу на поле чертежа должна располагаться основная надпись. На чертежах выполняется основная надпись формы 1 (ГОСТ2.104–2006) (§ 2.2).

Компоновка чертежа

Компоновка чертежа – это размещение на формате изображений, размеров и надписей (рис. 19).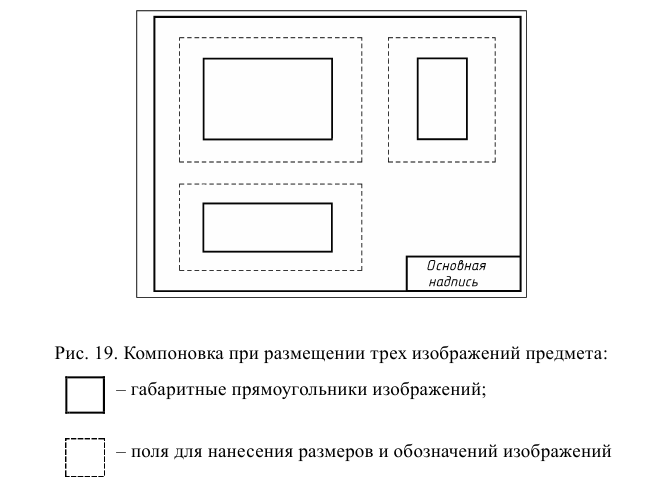

Изображения на поле чертежа должны быть расположены равномерно. Для выполнения этого требования, зная размеры изображаемого предмета и количество изображений, в первую очередь на чертеже размещают габаритные прямоугольники, размеры которых равны размерам изображений. При этом необходимо предусмотреть поля для нанесения размеров и надписей.

Наилучший результат компоновки чертежа получается при выполнении следующих действий:

1. по габаритным размерам изображений на тонком чистом листе бумаги построить прямоугольники (габаритные);
2. вырезать прямоугольники по контуру;
3. передвижением прямоугольников по полю чертежа найти оптимальные места для расположения изображений;
4. перенести контуры прямоугольников на поле чертежа;
5. внутри полученных габаритных прямоугольников выстраивать изображения на чертеже.

Проведение линий чертежа

Первоначально построение всех фигур чертежа и надписей выполняется тонкими линиями остро заточенным твердым карандашом без нажима, так называемое построение чертежа «в тонких линиях». Усиление нажима на карандаш или обводка элементов чертежа недопустимы до окончательного завершения построения чертежа и его тщательной проверки.

Прямые линии проводят без нажима на карандаш, чтобы в случае ошибки можно было стереть линию и провести ее в новом месте. Необходимо избегать проведения лишних линий, длинных засечек и т. п., нужно стараться реже пользоваться ластиком (его применение загрязняет чертеж). Проводя линии, карандаш следует располагать почти перпендикулярно к поверхности бумаги с незначительным наклоном в сторону движения (рис. 20), при этом он должен слегка соприкасаться с краем линейки или треугольника. Карандаш надо держать тремя пальцами недалеко от места его заточки. Левая рука должна придерживать линейку.

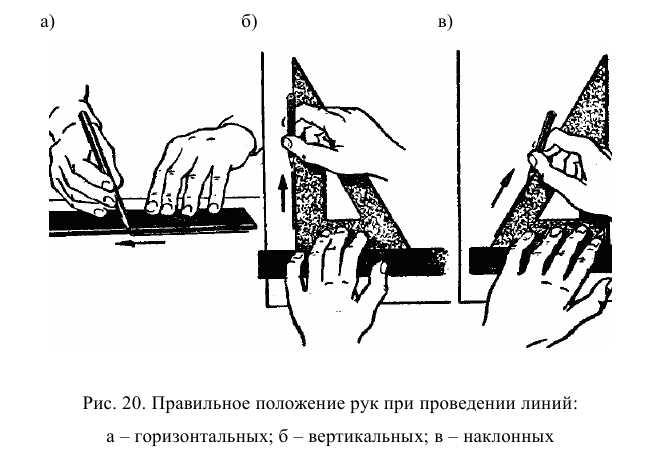
При проведении дуги окружности ножку циркуля ставят в центр. Циркуль вращают за головку большим и указательным пальцами в направлении движения часовой стрелки (рис. 21). Короткая ножка с карандашной вставкой и игла циркуля в рабочем положении должны быть параллельны друг другу, концы грифеля и иглы должны находиться на одном уровне. Во время вращения циркуль можно немного наклонять вперед.

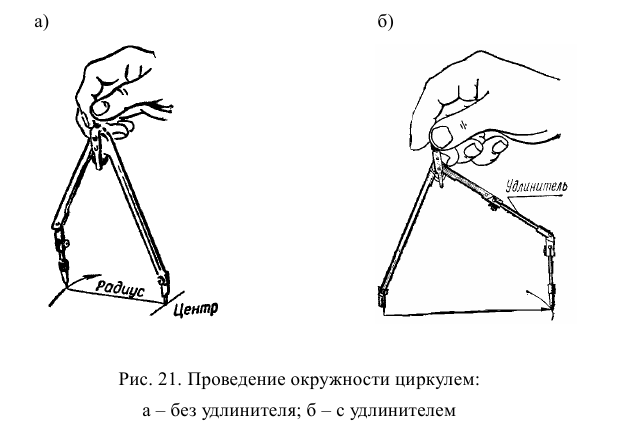
Параллельные линии на чертеже можно провести при помощи линейки и треугольника или при помощи двух треугольников (рис.22), а также можно использовать рейсшину.

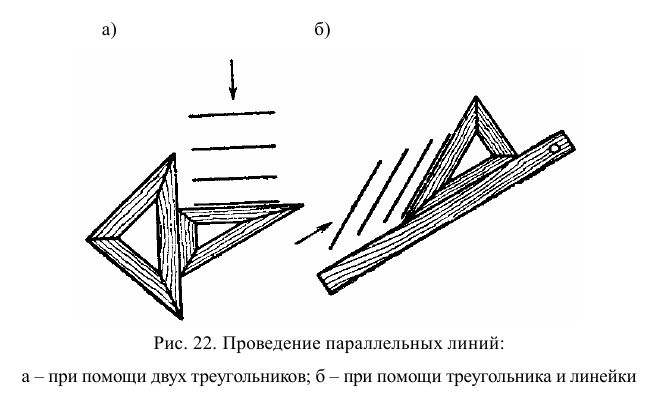
Выполнение изображений всегда начинают с проведения осевых линий (оси симметрии изображения) и центровых линий (центры окружностей и дуг окружностей). Осевые и центровые линии выполняются штрихпунктирными (ГОСТ 2.303–68) (§ 2.4). Рекомендуемое начертание линии на формате А3 приведено на рис. 23. Выбранный вариант должен быть выдержан на всем поле чертежа. Штрихпунктирные линии с другими линиями чертежа и между собой должны пересекаться только по длинному штриху (рис. 24).

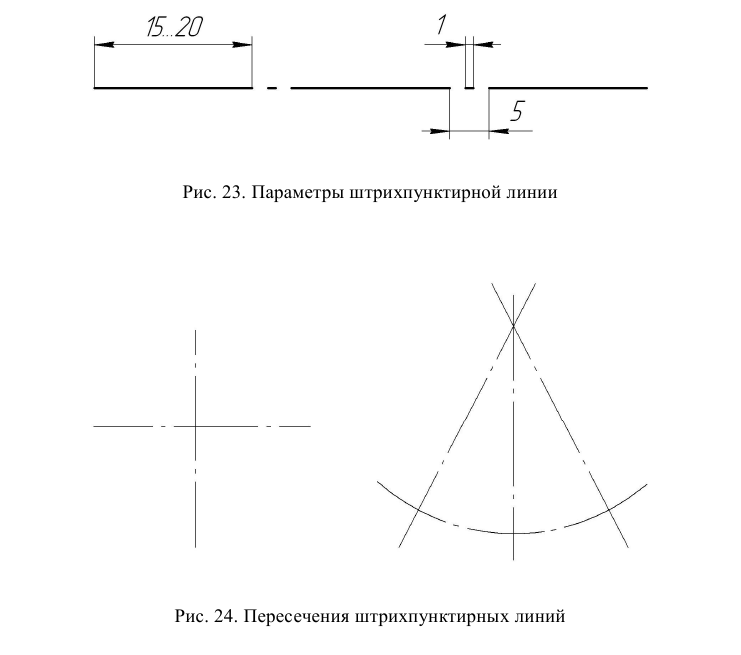
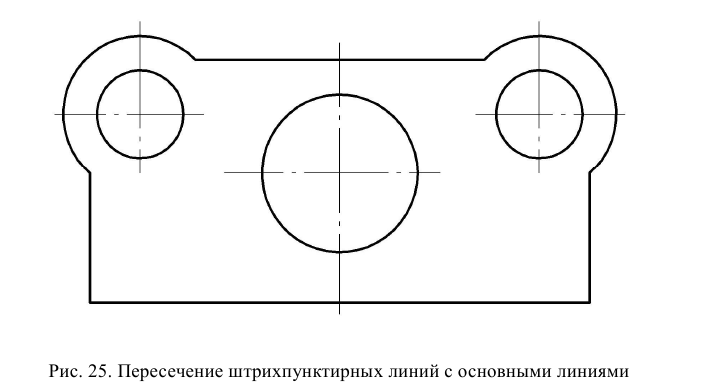
Штрихпунктирные линии должны пересекаться с линиями контура по длинному штриху и выходить за контур изображения на расстояние не более 5 мм. Для формата А3 это расстояние рекомендуется уменьшить до 2…3 мм (рис. 25).

Выполнение изображений

Изображения на чертеже выполняются по размерам задания в указанном масштабе. Для графической работы №1 «Геометрическое черчение» задание необходимо взять в ауд. 1-601 по варианту, указанному преподавателем. Рекомендуемый масштаб чертежа 1:1.

При выполнении изображений в ГР «Геометрическое черчение» решаются задачи геометрических построений: построение правильных многоугольников (§ 4.2), конических элементов заданной конусности (§ 4.3), сопряжений (глава 5) и т. д. графическими способами.

В задачах с прямолинейным контуром при построении горизонтальных и вертикальных участков контура необходимо строго выдерживать перпендикулярность линий рамке чертежа и параллельность линий друг другу. При построениях все размеры следует откладывать либо по металлической или пластмассовой линейке, либо используя циркуль-измеритель. Штриховка при выполнении чертежа в тонких линиях не наносится, так как обвести множество параллельных линий без сдвига – трудоемкая задача. Штриховка выполняется при обводке чертежа (без подготовки), но разметку для штриховки выполняют на подготовительном этапе. Штриховка металлов выполняется параллельными прямыми линиями, расположенными под углом 45° к рамке чертежа (ГОСТ 2.306–68) (§ 2.6).

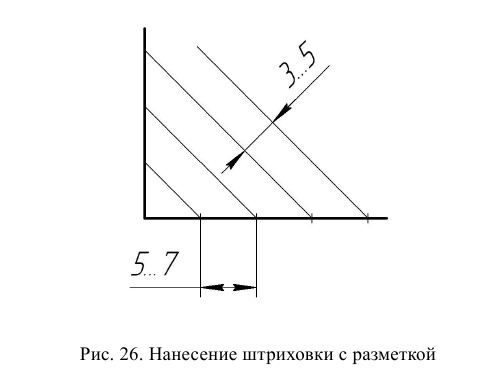
Штриховка различных деталей наносится либо с разным расстоянием между линиями штриховки, либо с разным наклоном (вправо или влево). Расстояние между линиями штриховки выбирают 1…10 мм в зависимости от площади штриховки и величины изображений. Для формата А3 рекомендуется выполнять штриховку через 3…5 мм. Разметку штриховки нецелесообразно выполнять на поле штриховки, так как это будет заметно при малейшем отклонении от разметки. Выполнять разметку следует на линиях основного контура при прямолинейном контуре изображения или по рамке чертежа при криволинейном контуре изображения (рис. 26).

Выполнение надписей и нанесение размеров

Чертежные шрифты, применяемые для нанесения всех надписей на чертежах и других технических документах, установлены ГОСТ 2.304–81 (§ 2.5).

При выполнении учебных чертежей следует использовать шрифт типа Б:

1. для размерных чисел и знаков – шрифт 5 с наклоном;
2. для выполнения надписей на поле чертежа – шрифт 7 с наклоном;
3. при заполнении основной надписи:

• – фамилии – шрифт 3,5 с наклоном;
• – обозначение чертежа – шрифт 7 без наклона;
• – остальные графы – шрифт 7 с наклоном.

Прежде чем приступить к выполнению надписей, следует хорошо изучить конструкцию букв и цифр шрифта (рис. 9, 10 и 11). Надпись следует выполнять по крупной сетке (рис. 8 и 12), ограничивая высоту букв, цифр, расстояние между ними, исходя из размера шрифта h. Расчет необходимо вести, опираясь на таблицу из ГОСТ 2.304–81 (табл. 8 и 9).

Выполнение надписей проводят в следующей последовательности:

1. на месте, отведенном для надписи, проводят две параллельные линии на расстоянии, соответствующем высоте прописных букв и цифр;
2. если надпись содержит строчные буквы, проводят дополнительные параллельные линии, ограничивающие их высоту и выступающие элементы;
3. от начала надписи размечают ширину всех букв, цифр, знаков, расстояния между ними;
4. через полученные точки разбивки проводят параллельные прямые под углом, соответствующим углу наклона шрифта (75° или 90°);
5. в полученные четырехугольники вписывают соответствующие буквы, цифры, знаки (рис. 8 и 12).

Указанный порядок выполнения надписей рекомендуется как для крупных, так и для мелких надписей. В дальнейшем, когда шрифт будет хорошо изучен, можно не строить четырехугольники для каждой буквы и цифры, а провести ряд произвольных штрихов под углом, принятым для данного шрифта (75° или 90°). Однако две параллельные линии, устанавливающие высоту надписи, проводить обязательно.

Для облегчения выполнения и чтения чертежа при простановке размеров необходимо учитывать следующие требования (рис. 27):

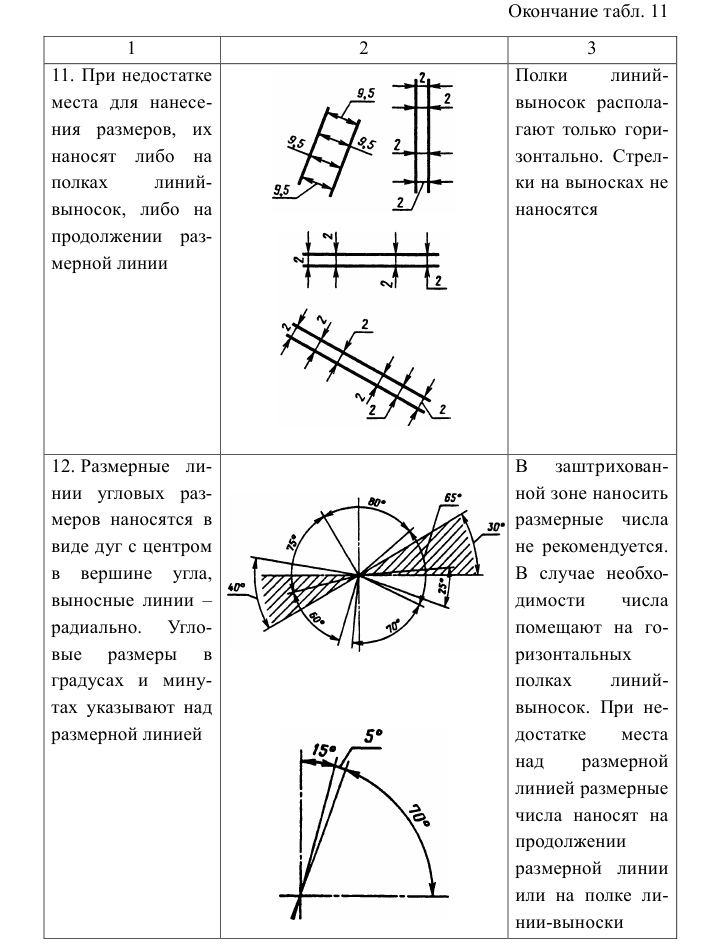
1. наносить размеры рекомендуется вне контура изображения; расстояние между параллельными размерными линиями должно быть не менее 7 мм (для шрифта 5 не менее 10 мм)
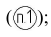
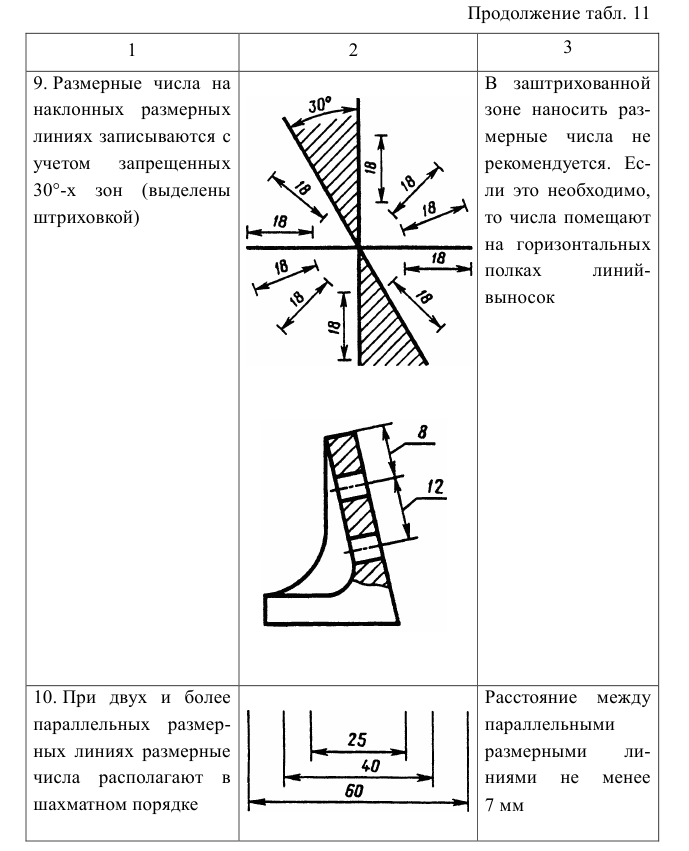
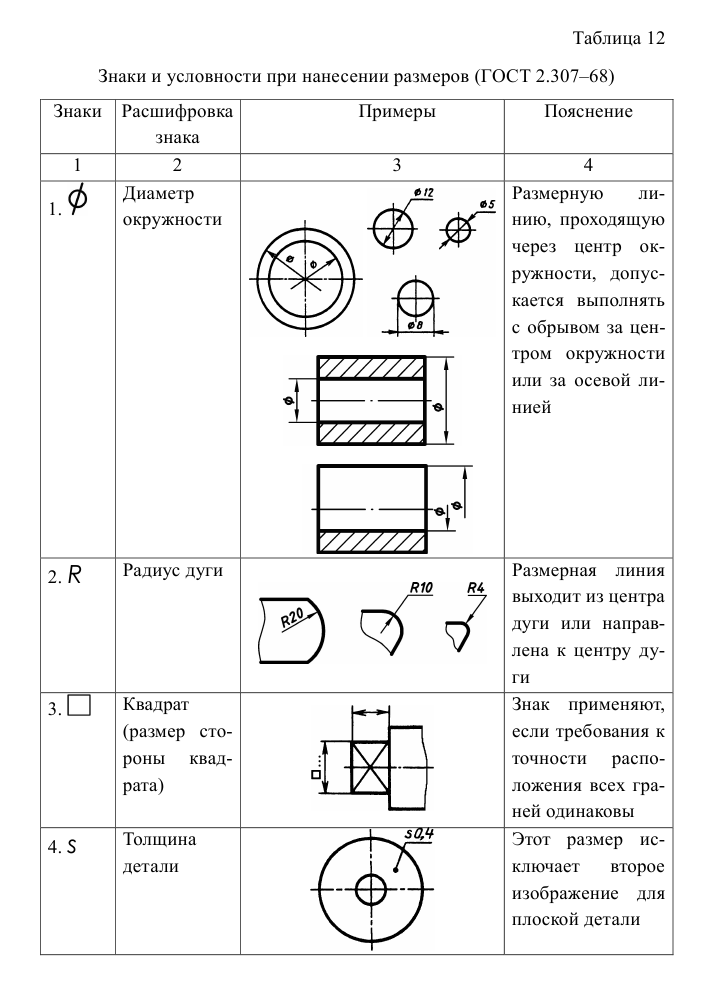
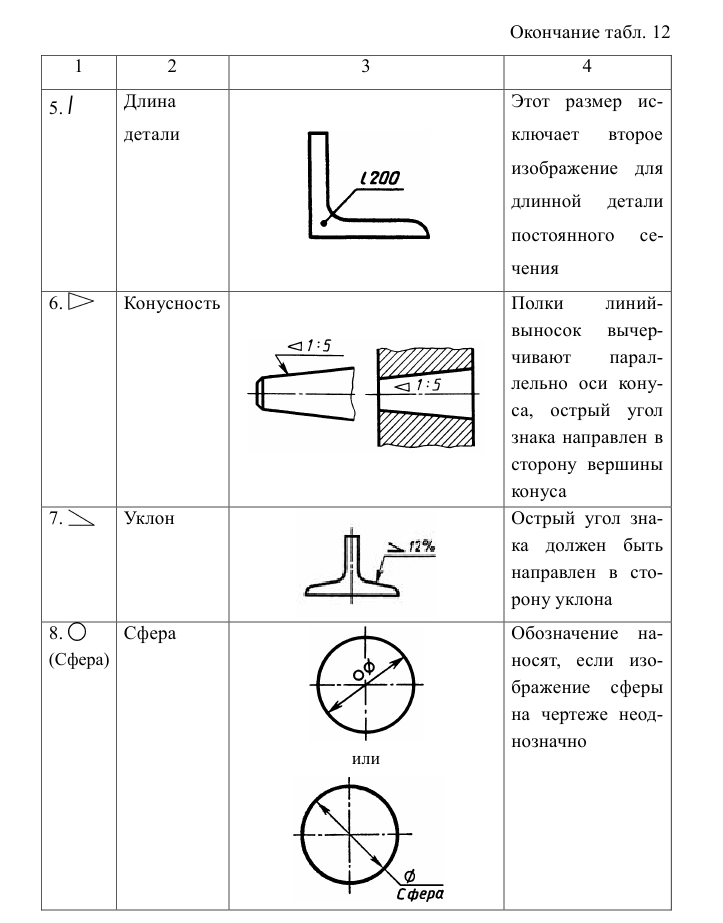
2. размерные числа на наклонных размерных линиях не наносить, а проставлять на полках линий-выносок, которые могут располагаться только горизонтально
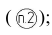
3. выстраивать размеры рекомендуется в единую размерную цепь, не сдвигая размерные линии относительно друг друга
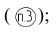
4. наносить размерные числа над размерной линией на расстоянии 1мм, как можно ближе к ее середине

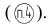
Обводка чертежа

Закончив построение чертежа, тщательно проверяют правильность проведения линий, а также наличие лишних линий. Лишние линии или участки линий (так же, как и загрязнения, образовавшиеся на чертеже) удаляют до обводки чертежа. Удаление таких линий после обводки может занять много времени.

Подготовка чертежа к обводке

Перед обводкой чертежа нужно мягким ластиком удалить с листа пятна, оставшиеся от прикосновения к бумаге чертежных принадлежностей или пальцев, и лишние участки линий.

При удалении лишних участков линий должны выполняться следующие требования (для формата А3):

• – осевые линии должны выходить за изображение на 2…3 мм;
• – центровые линии должны выходить за окружность или дугу на 2…3 мм, пересекаясь с любыми линиями чертежа по длинному штриху;
• – выносные линии за размерные должны выходить на 2…3 мм;
• – полки линий-выносок должны выходить за последний знак надписи на 2…3 мм.

Линии построений (геометрическое решение задачи) убирать с поля чертежа не надо (они помогут при обводке), но и обводить их ярко нет необходимости, так как данные линии не относятся к линиям чертежа, установленным ГОСТ 2.303–68.

Подготовка чертежных инструментов

Для обводки тонких линий толщиной приблизительно равной 0,5 мм необходимо подготовить карандаш ТМ или М, заточив его «на острие» (рис. 14б), чтобы линия получалась черная, четкая. В процессе обводки грифель постепенно притупляется, поэтому его надо регулярно подтачивать, чтобы сохранить нужную толщину линий.

Для обводки основного контура толщиной s»1 мм необходимо подготовить карандаш М, заточив его «лопаткой»: снять грифель параллельными срезами, а затем срезать острый конец, чтобы ширина среза была приблизительно равна 1 мм (рис. 14а).

При обводке чертежа возникает проблема достижения одинаковой толщины и яркости прямых линий и окружностей: часто циркульные кривые получаются более светлыми, чем прямые линии и лекальные кривые. Объясняется это тем, что на пишущий стержень, поставленный в циркуль, нельзя нажать так же сильно, как на карандаш. Поэтому в циркуль нужно ставить более мягкий пишущий стержень, чем стержень используемого карандаша.

Грифель в циркуле должен быть:

• – М для тонких линий;
• – 2М для толстых линий.

Грифель в циркуле необходимо подготовить тем же способом, что и грифель карандаша.

Последовательность обводки чертежа

Тщательно и качественно выполненный «в тонких линиях» чертеж можно испортить в процессе обводки, если не придерживаться определенного порядка и правил обводки чертежа. Главное условие правильной обводки чертежа – это такой нажим на карандаш, при котором линии получались бы четкими, яркими и черными.

Порядок обводки чертежа:

• – обводка тонких линий;
• – обводка надписей и размерных чисел;
• – обводка толстых сплошных основных линий;
• – обводка основной надписи;
• – обводка рамки чертежа.

Обводка тонких линий

При обводке чертежа карандаш необходимо держать вертикально, чуть наклоняя в сторону обводки. На карандаш нужно нажимать для того, чтобы линии были яркими, черными. Так как грифель карандаша достаточно мягкий, он будет быстро стачиваться. Выполненная правильно заточка карандаша (рис. 14б) позволит заострять его, не затачивая заново. Заострять грифель карандаша необходимо постоянно, чтобы все тонкие линии имели постоянную толщину (примерно 0,5 мм) и яркость.

В первую очередь обводят все горизонтальные прямые линии: сплошные, штрихпунктирные, штриховые. Передвигать инструмент следует сверху вниз по полю чертежа, чтобы линии меньше размазывались. Инструмент (линейка, угольник) прикладывается к линии так, чтобы можно было обвести ее целиком, не передвигая инструмент. В противном случае возникнет наложение обведенных участков друг на друга и погрешность обводки будет заметна. При обводке горизонтальных линий не следует забывать об обводке тонких линий в основной надписи (рис. 6).

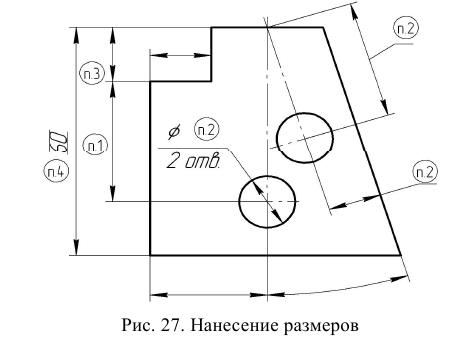
Далее обводят все вертикальные линии, передвигая инструмент слева направо. Затем наклонные прямые. После этого обводят дуги и окружности. Линии построений оставляют без обводки. В последнюю очередь проводят линии штриховки. Поскольку линии штриховки при выполнении чертежа в тонких линиях не наносятся, штриховку необходимо выполнять сразу при обводке. Используя разметку штриховки (рис. 26) устанавливают инструмент под углом 45° к рамке чертежа и проводят тонкие параллельные линии в области штриховки. Линии штриховки пересекают любые линии чертежа без разрывов. Разрывать линии штриховки необходимо только на стрелках размерных линий и размерных числах (рис. 28).

Обводка надписей и размерных чисел

При обводке надписей следует учитывать, что рука опирается на лист, в отличие от обводки линий, когда она не касается листа. В связи с этим, чтобы не допустить размазывания уже обведенных линий, необходимо под руку подкладывать чистый лист бумаги.

В первую очередь обводят размерные числа шрифтом 5 (толщина обводки 1/10h = 0,5 мм), используя тот же острозаточенный карандаш, что и для обводки тонких линий.

Порядок обводки размерных чисел тот же, что и для обводки тонких линий:

• – горизонтальные (сверху вниз);
• – вертикальные (слева направо);
• – наклонные.

После этого приступают к обводке надписей шрифтом 7 (толщина обводки 1/10h = 0,7 мм). Карандаш в этом случае необходимо чуть затупить. При обводке надписей не используют чертежные инструменты, поэтому рука быстро устает от напряжения и линии получаются неровные. Чтобы избежать этого, необходимо давать отдых руке примерно 5 минут.

Для обводки прямолинейных участков букв и цифр крупных шрифтов (начиная с размера 10) можно использовать линейку. При обводке надписей шрифтом 3,5 (толщина обводки 1/10h = 0,35 мм) используют острозаточенный карандаш ТМ.

Обводка линий основного контура и рамки чертежа

Для формата А3 рекомендуемая толщина обводки линий основного контура, толстых линий в основной надписи и рамки чертежа приблизительно 0,8 - 1 мм, т. е. она должна быть примерно в два раза толще, чем тонкие линии (ГОСТ 2.303–68). Для обводки прямых линий контура используется карандаш М, заточенный «лопаткой» (рис. 14а). Такая заточка карандаша позволит выдержать необходимую толщину линий. Для обводки криволинейных участков контура мягкость грифеля в циркуле должна быть 2М.

Если изображение содержит только прямолинейный контур, то порядок обводки тот же, что и для тонких линий. Если контур изображения криволинейный, то порядок обводки меняется. В первую очередь обводятся окружности и дуги окружностей, начиная с дуг меньшего диаметра. Если дуги окружностей находятся в сопряжении, то они обводятся только до найденных точек сопряжений (глава 5).

Рекомендации, которые надо соблюдать неукоснительно: ни в коем случае при обводке дуг и окружностей нельзя нажимать на ножку циркуля (иначе она сдвинется), нельзя обводить линии от руки по уже проведенным тонким линиям или тушевать плохо обведенные толстые линии.

После обводки криволинейного контура переходят к обводке прямолинейного контура в установленном порядке: сначала все горизонтальные линии, передвигая линейку сверху вниз, затем все вертикальные линии, передвигая линейку слева направо, после этого все наклонные линии.

При обводке линий по линейке необходимо прикладывать линейку так, чтобы линию можно было обвести целиком (длина линейки не должна быть меньше длины обводимой линии). Обводку линий основного контура надо выполнять очень внимательно, так как неправильно проведенные яркие толстые линии трудно убрать с чертежа без остатка.

Нельзя забывать про обводку основной надписи и рамки чертежа. Если при обводке чертежа возникли погрешности, которые студент не знает, как устранить самостоятельно, необходимо обратиться за консультацией к преподавателю.

После обводки чертежа необходимо тщательно проверить готовый чертеж:

• – все ли линии обведены;
• – выдержана ли толщина и яркость обведенных линий;
• – все ли надписи обведены;
• – не осталось ли на чертеже погрешностей обводки.

После этого можно считать чертеж готовым к сдаче. Перед защитой чертежа необходимо подготовится к ответу на контрольные вопросы (с. 94). При транспортировке готового чертежа в тубусе (при сворачивании в рулон) необходимо предохранить чертеж от размазывания, проложив чистыми белыми (тонкими) листами.

Геометрические построения на плоскости

Для построения изображений на чертежах необходимо овладеть навыками выполнения геометрических построений на плоскости:

• – деление отрезков прямых и углов; построение перпендикуляра к прямой
• – деление окружности на равные части; построение правильных многоугольников
• – построение уклона и конусности
• – построение сопряжений

Деление отрезков прямых и углов

Деление отрезка пополам

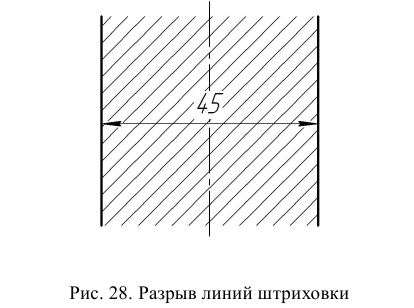
Отрезок АВ прямой m (рис. 29) делится на две равные части перпендикуляром n, проведенным через точки С и D пересечения дуг окружностей радиуса R > 0,5АВ с центрами в точках А и В соответственно. Точка Е – середина отрезка АВ.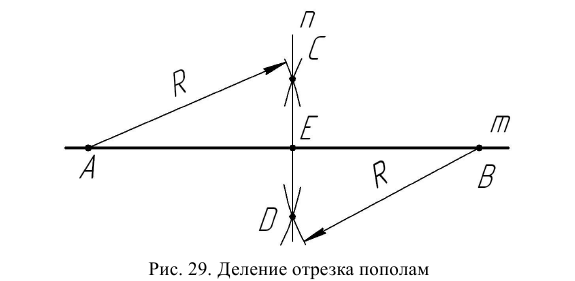

Построение перпендикуляра к прямой m через точку А, не лежащую на прямой. Дугой произвольного радиуса R из точки А (рис. 30а) пересечь прямую m в точках В и С. Используя эти точки как центры, провести одинаковыми произвольными радиусами дуги окружностей до их взаимного пересечения в точке О. АО 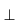m.

Построение перпендикуляра из точки А, принадлежащей прямой m. Провести из произвольно выбранного центра О (рис. 30б), расположенного вне прямой m, дугу окружности R = ОА и отметить точку пересечения В с прямой. Провести диаметр ВМ через точку О. МА 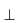АВ, так как угол МАВ вписан в окружность и опирается на ее диаметр.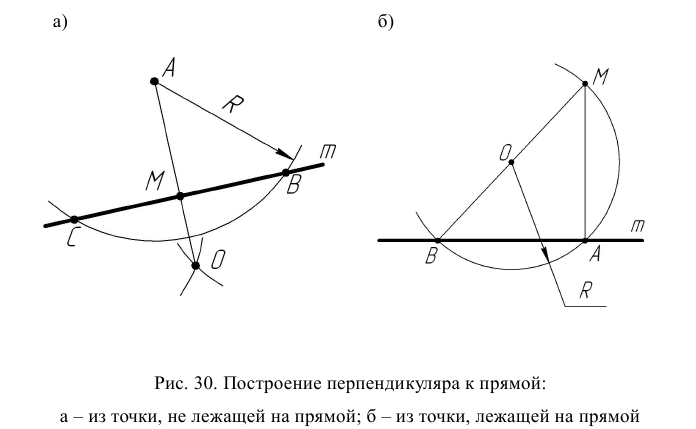

Деление отрезка на заданное число частей

Отрезок АВ прямой m (рис. 31а) разделить на пять равных частей. Провести вспомогательный луч t под острым углом к прямой m через точку А. На луче t от точки А отложить пять равных отрезков произвольной длины (отмечены точками 1, 2, 3, 4, 5). Последнюю точку 5 соединить с точкой В и последовательно из каждой точки деления луча t провести ряд прямых, параллельных прямой 5В, до пересечения с прямой m. Полученные точки 1’, 2’, 3’, 4’, 5’ делят отрезок АВ на пять равных частей.

Деление отрезка на пропорциональные части

Выполняется по аналогии с делением отрезка на заданное число частей. Отрезок прямой АВ (рис. 31б) разделить в соотношении 2:5. На вспомогательном луче t отложить сумму отрезков, составляющих данное соотношение (2 + 5 = 7).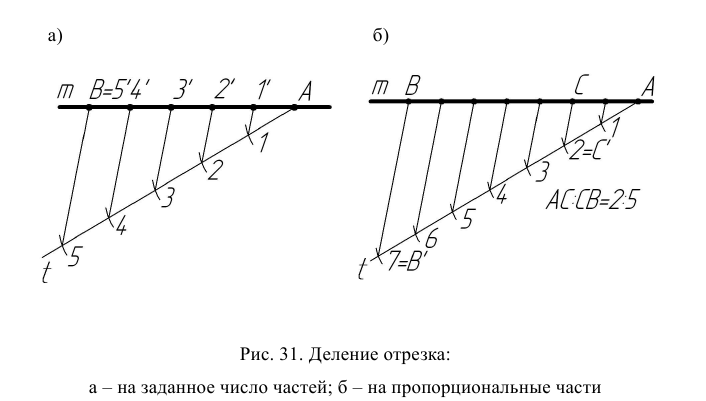

Деление угла пополам

Из вершины О заданного угла (рис. 32) провести дугу произвольного радиуса R до пересечения со сторонами m и n в точках А и В. Из полученных точек провести две дуги одинакового, произвольного радиуса R 1 до их взаимного пересечения в точке М. Отрезок ОМ делит угол пополам.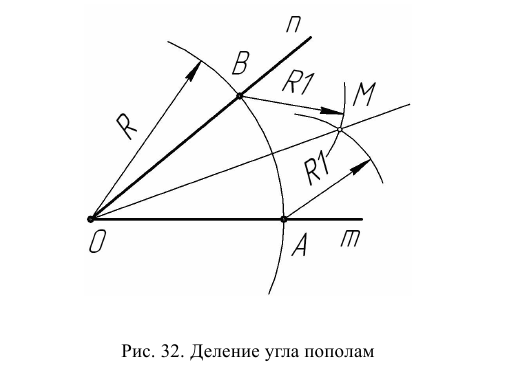

Построение угла 30°

Построить прямой угол АОВ. Из точки О (рис. 33а) провести дугу произвольного радиуса R. Из точки А дугой того же радиуса R сделать засечку на дуге АВ в точке М. Угол МОВ = 30°.

Построение угла 60°

Из точки О (рис. 33б) на прямой m провести дугу окружности произвольного радиуса R. Из получившейся точки пересечения А провести дугу того же радиуса R до пересечения с первой дугой в точке В. Угол АОВ = 60°.

Построение угла 75°

Построить прямой угол АОВ. Повторить построение угла ВОМ = 60° (рис. 33б) и дополнить построением биссектрисы ОС (рис. 33в) угла АОМ. Угол СОВ = 75°.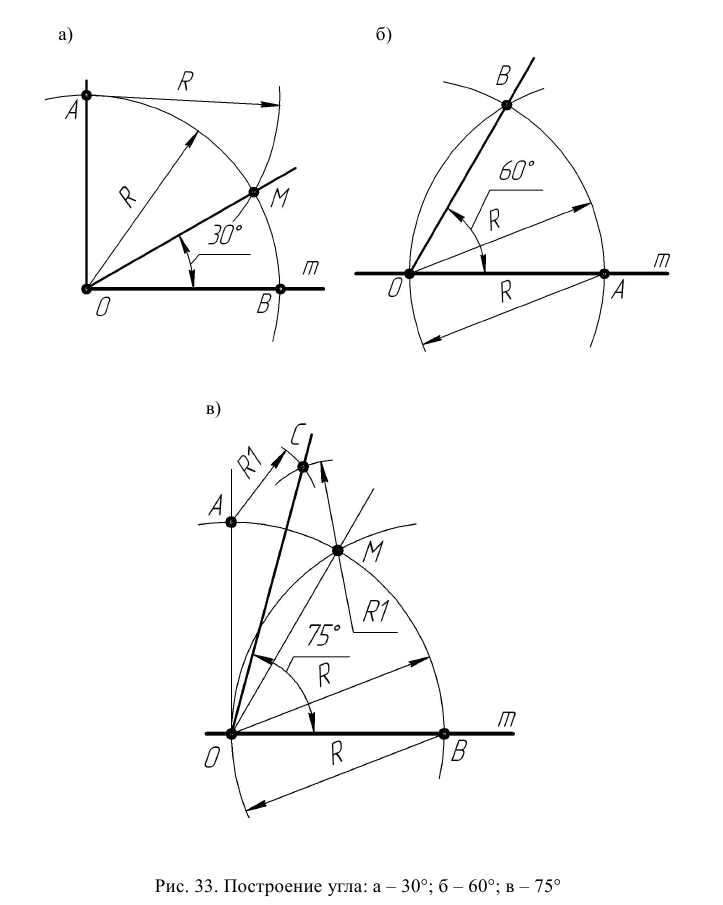

Построение углов при помощи чертежных треугольников

Наиболее часто встречающиеся в черчении углы 15°, 30°, 45°, 60°, 75° и 90° можно построить при помощи линейки и треугольника, двух треугольников, а также составляя различные комбинации расположения инструментов для получения угла заданной величины (рис. 34).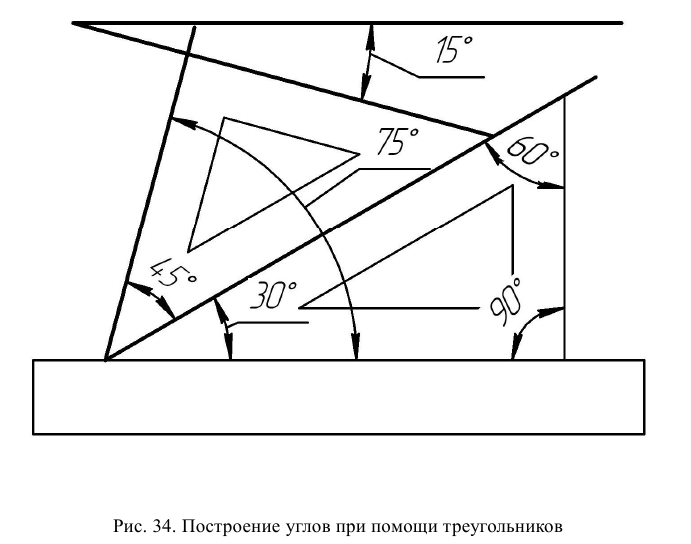

Деление окружности на равные части. Построение правильных многоугольников

Определение центра дуги

Наметить на дуге окружности три произвольно расположенные точки А, В, и С (рис. 35а). Соединить точки прямыми АВ и ВС для получения хорд данной дуги. Точка пересечения перпендикуляров, проведенных через середины хорд (рис. 29) определяет положение центра исходной дуги. Аналогично выполняется построение дуги через три произвольные точки.

Определение центра окружности

В заданной окружности (рис. 35б) провести две непараллельные друг другу хорды АВ и СD. Через середины хорд провести перпендикуляры, пересечение которых определит положение центра исходной окружности. Определить центр окружности можно, воспользовавшись построениями для определения центра дуги.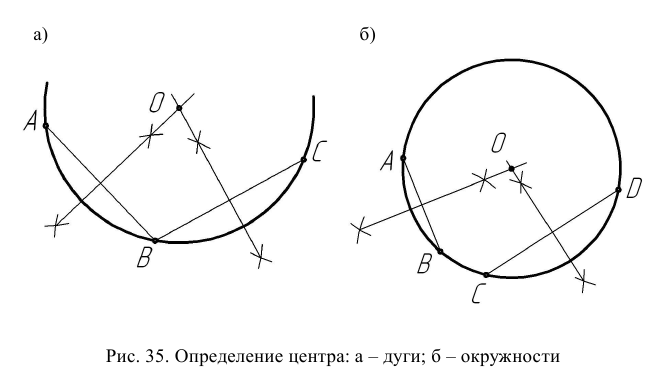

Деление окружности на четыре и восемь частей. Два взаимно перпендикулярных диаметра делят окружность на четыре равные части (рис. 36а). Соединив точки А, В, С и D, можно получить вписанный квадрат. Для деления окружности на восемь частей необходимо дуги между точками А и С, В и С разделить пополам при помощи циркуля или транспортира (рис. 36б). Точки деления соединить с центром окружности и продолжить прямые до пересечения с противоположной половиной окружности. Соединив точки деления, можно получить правильный вписанный восьмиугольник.

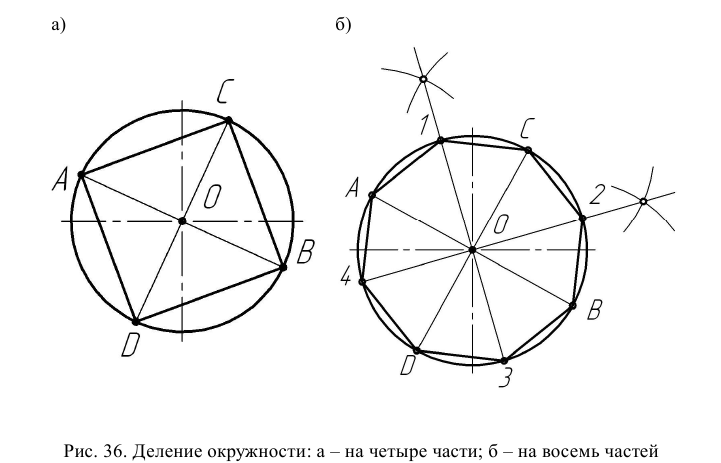
Деление окружности на три и шесть частей

Из точки В вертикального диаметра, как из центра, радиусом заданной окружности проводят дугу, пересекающую окружность в точках С и D (рис. 37а). Соединив точки А, С и D, можно получить правильный вписанный треугольник. Из точек А и В горизонтального диаметра радиусом заданной окружности проводят дуги, пересекающие окружность в точках 1, 2, 3 и 4 (рис. 37б). Соединив точки деления между собой, а также с А и В, можно получить правильный вписанный шестиугольник.

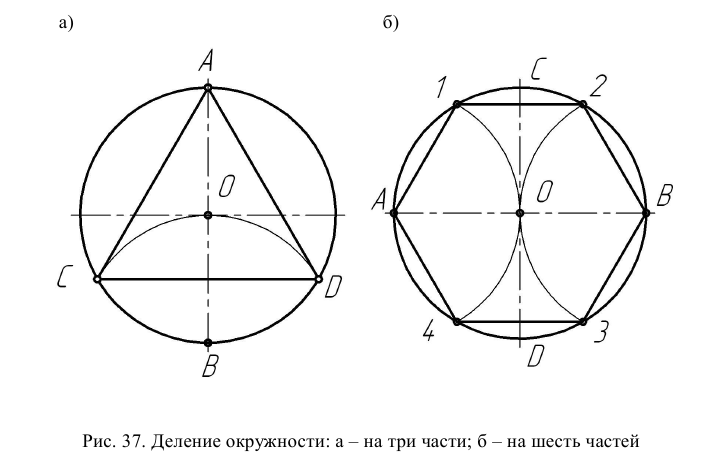
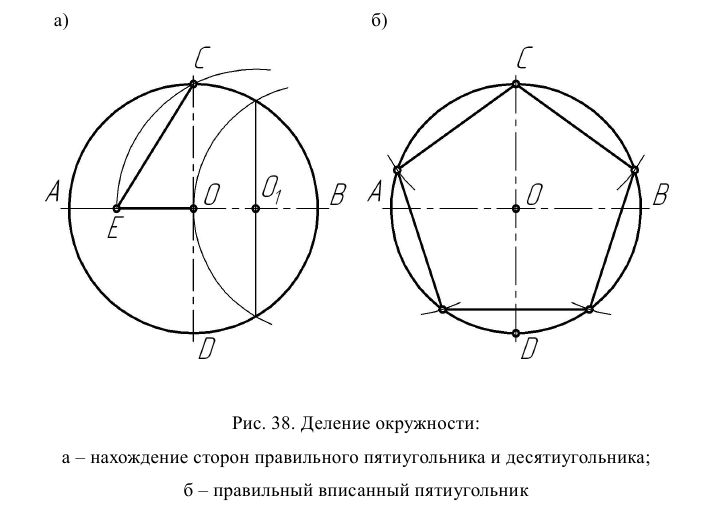
Деление окружности на пять и десять частей. Для определения размера стороны правильного пятиугольника радиус окружности ОВ делят на две равные части и, принимая точку за центр, проводят дугу радиусом, равным отрезку C (рис. 38а). Эта дуга пересекает горизонтальную ось окружности в точке Е. Отрезок ЕС равен величине стороны правильного вписанного пятиугольника (рис. 38б), а отрезок ЕО приближенно равен стороне правильного вписанного десятиугольника.

Построение квадрата по заданной стороне

Провести прямую m под углом 45° к диагонали квадрата (рис. 39). На прямой m найти симметричные точки А и В, исходя из размера стороны квадрата. Через полученные точки провести прямые, перпендикулярные прямой m.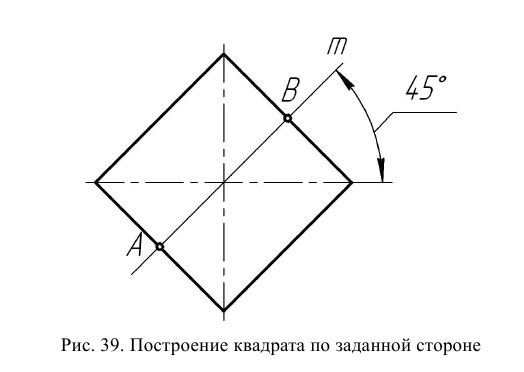

Построение уклона и конусности

Уклоном называется мера наклона одной линии или плоскости по отношению к другой. Величина уклона характеризуется тангенсом угла наклона линии, т. е. отношением противолежащего катета к прилежащему.

Для построения уклона 1:4 (рис. 40) от точки А откладываются четыре равных отрезка произвольной длины. Из полученной точки С восставляется перпендикуляр, на котором откладывается один отрезок такой же величины. Прямая, проведенная через точки А и В, имеет уклон 1:4 по отношению к прямой АС. Отношение, выраженное простой дробью, показывает уклон прямой АВ к прямой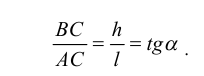

Уклон может выражаться отношением (простой дробью), в процентах или градусах. Перед числовым отношением, характеризующим уклон, наносят знак « », причем острый угол этого знака направляют в сторону уменьшения уклона (ГОСТ 2.307–68). Нормальные углы уклона устанавливает ГОСТ 8908–58.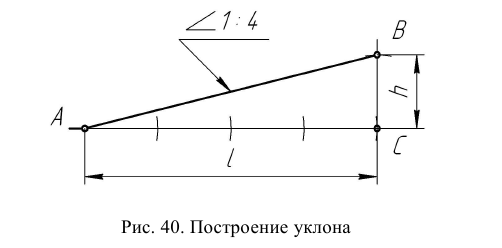

Построение прямой а, имеющей заданный уклон и проходящей через точку М, выполняют, используя прямоугольный треугольник с единичным катетом (ВС = h – любой единичный отрезок). Прямая а, параллельная АВ, имеет тот же уклон (рис. 41).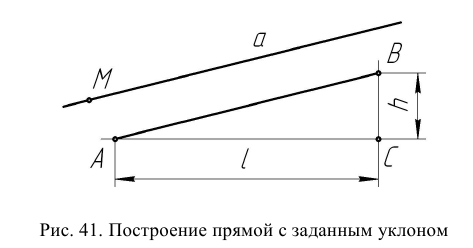

Конусностью называется отношение диаметра окружности основания прямого кругового конуса к его высоте (рис. 42): К = d : h .

Для построения заданной конусности К = 1:3 необходимо построить две взаимно перпендикулярные прямые, затем из точки М на вертикальной прямой откладываются два равных отрезка МА и МВ, а на горизонтальной – отложить три отрезка, равных АВ. Таким образом получается, отрезок АВ – диаметр основания конуса, СМ – высота конуса (СМ = 3АВ), а отрезки СА и СВ – образующие конуса, имеющего заданную конусность К = 1:3.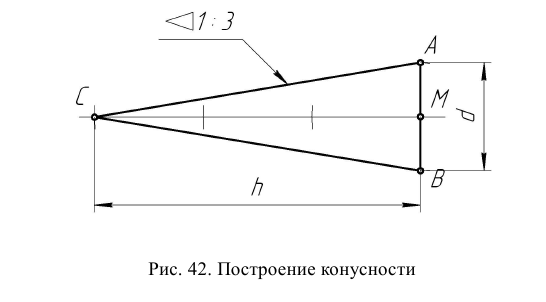

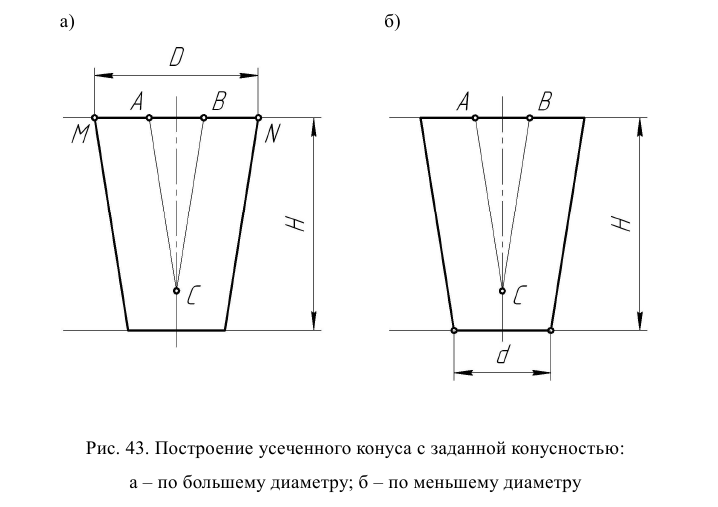
Построение усеченного конуса с заданным основанием D (большим) и высотой H, имеющего заданную конусность К (рис. 43а), выполняют, используя единичный конус. Построение единичного конуса, где АВ – любой единичный отрезок, показано на рис. 42. Опираясь на точки М и N – концы заданного диаметра D (рис. 43а), проводят прямые (образующие искомого конуса), параллельные прямым АС и ВС на участке, ограниченном заданной высотой Н. Построенный конус будет иметь ту же конусность, что и единичный конус. При этом знать размер меньшего основания конуса нет необходимости, так как оно получается само собой при построении. Аналогично проводят построение усеченного конуса, опираясь на заданный диаметр d (меньший) (рис. 43б).

Перед размерным числом, характеризующим конусность, наносят знак « < », острый угол которого должен быть направлен в сторону вершины конуса. Конусность следует наносить над осевой линией или на полке линии-выноски (рис. 44). Полка линии-выноски должна быть параллельна оси конуса. ГОСТ 8698–67 устанавливает следующий нормальный ряд конусностей: 1:0,289, 1:0,500, 1:0,652, 1:0,866, 1:1,207, 1:1,866, 1:3, 1:5, 1:7, 1:8, 1:10, 1:12, 1:15, 1:20, 1:30, 1:50, 1:100, 1:200.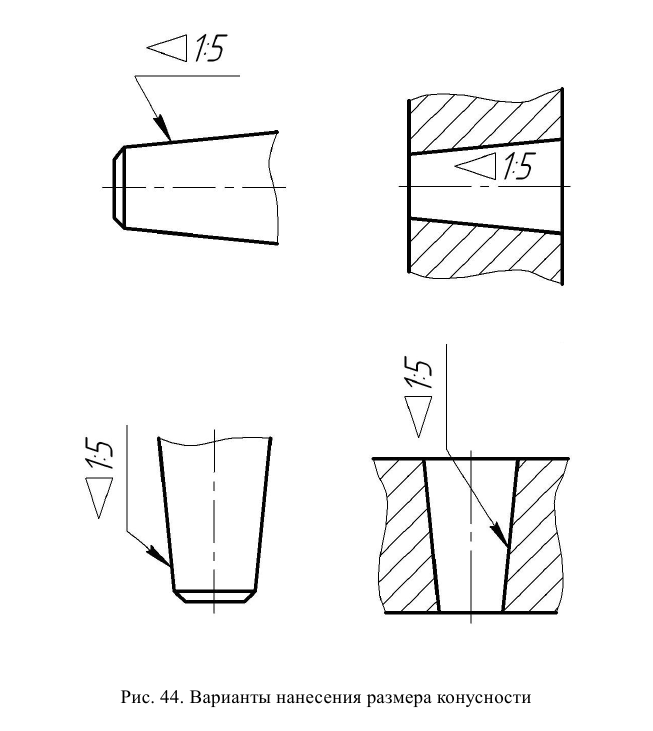

Построение сопряжений

Сопряжением называется плавный переход прямой линии в дугу окружности или одной дуги в другую. Общая для этих линий точка (точка перехода) называется точкой сопряжения. В основе алгоритма решения задач на построение сопряжений лежат следующие правила.

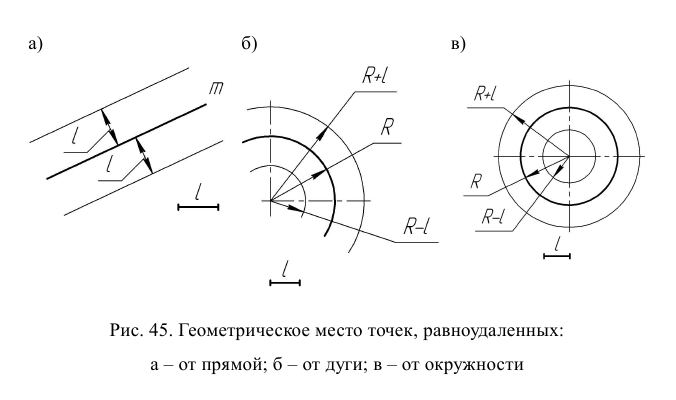
Правило 1. Геометрическое место точек, равноудаленных на заданное расстояние l от прямой m, есть прямая, параллельная исходной прямой и отстоящая от нее на расстоянии l (рис. 45а).

Правило 2. Геометрическое место точек, равноудаленных на заданное расстояние l от окружности (дуги), есть концентрическая окружность (дуга) по отношению к исходной, отстоящая от заданной на расстоянии l (рис. 45б, в).

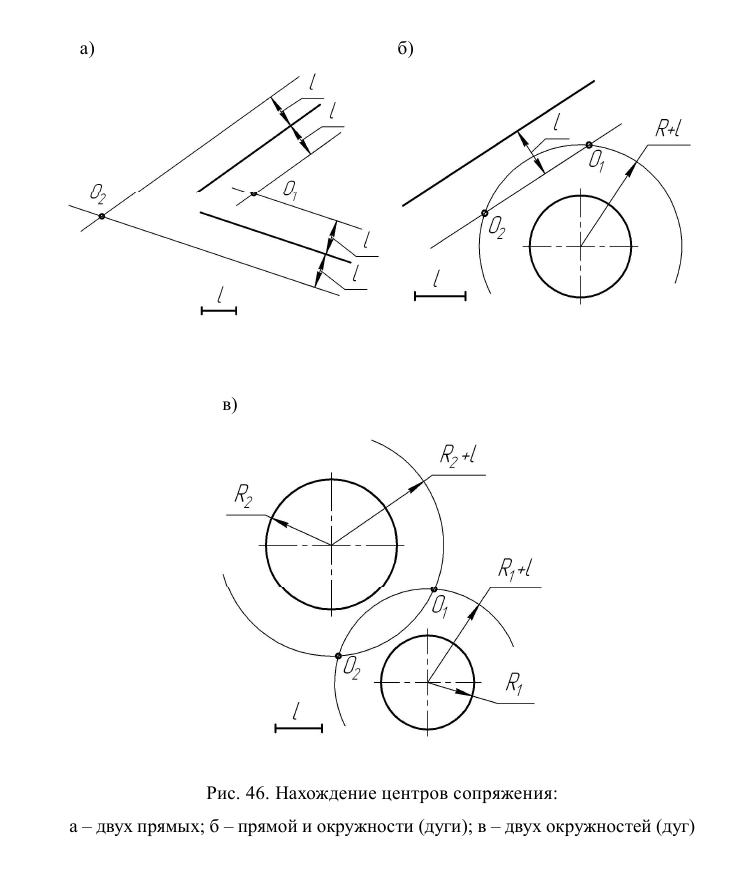
Правило 3. Точки 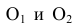(центры сопряжения), равноудаленные от двух прямых, прямой и окружности (дуги), двух окружностей (дуг), находятся на пересечении соответствующих линий (рис. 46).

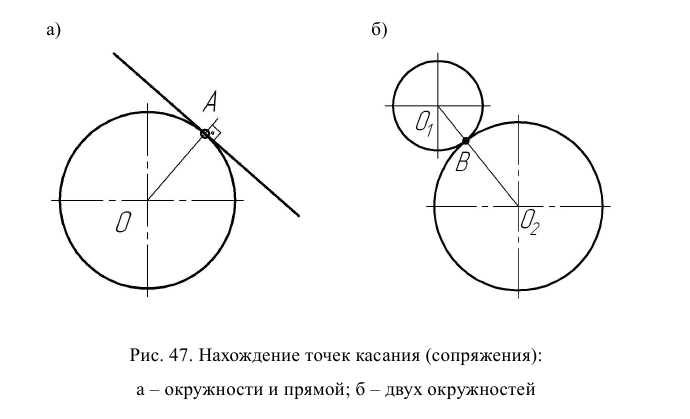
Правило 4. Точка касания (сопряжения) А прямой и окружности находится на линии, проведенной из центра окружности под прямым углом к прямой (рис. 47а). Точка касания В двух окружностей (дуг) находится на линии, соединяющей их центры (рис. 47б).

В общем случае решение задач на построение сопряжения двух линий дугой заданного радиуса описывается следующим алгоритмом:

• – построение множества точек, равноудаленных от первой линии на расстояние радиуса сопряжения (рис. 45);
• – построение множества точек, равноудаленных от второй линии на расстояние радиуса сопряжения (рис. 45);
• – определение центра дуги сопряжения на пересечении построенных множеств точек (рис. 46);
• – определение точек сопряжения на первой и второй сопрягаемых линиях (рис. 47);
• – проведение дуги сопряжения в зоне между точками сопряжения.

Используя правила, описанные в алгоритме решения задач на построение сопряжений (рис. 45–47), выполняют построения различных видов сопряжений и касательных (табл. 15 – табл. 23): 1. Построение касательных из точки к окружности (табл. 15); 2. Построение касательных к двум окружностям:

• – внешнее касание (табл. 16);
• – внутреннее касание (табл. 17);

3. Построение сопряжения двух прямых дугой заданного радиуса (табл. 18); 4. Построение сопряжения прямой и окружности дугой заданного радиуса:

• – внешнее касание (табл. 19);
• – внутреннее касание (табл. 20);

5. Построение сопряжения двух окружностей дугой заданного радиуса:

• – внешнее касание (табл. 21);
• – внутреннее касание (табл. 22);
• – смешанное касание (табл. 23).

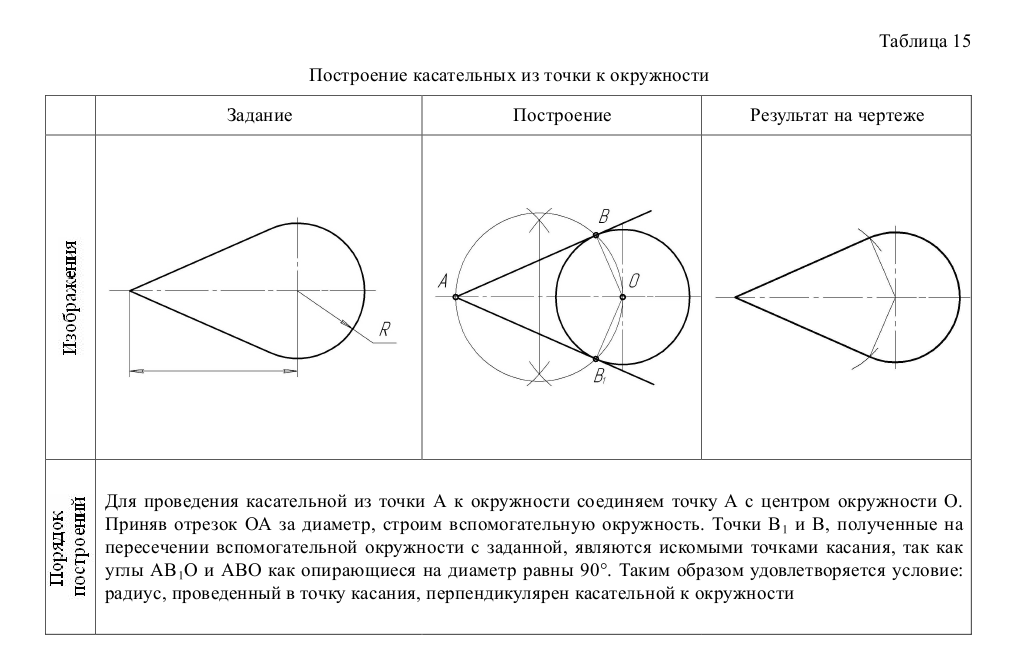
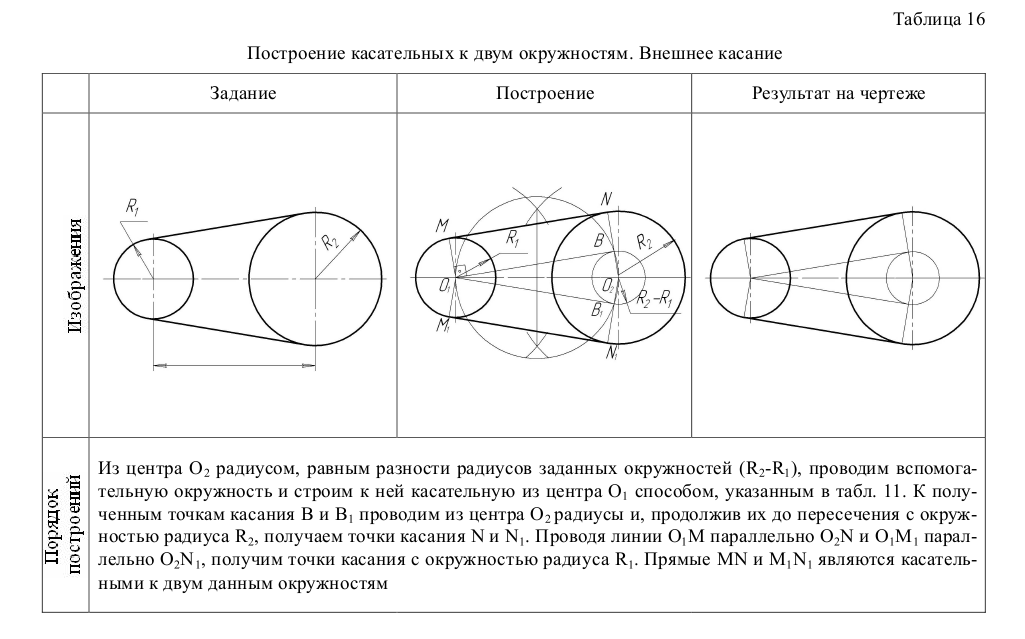
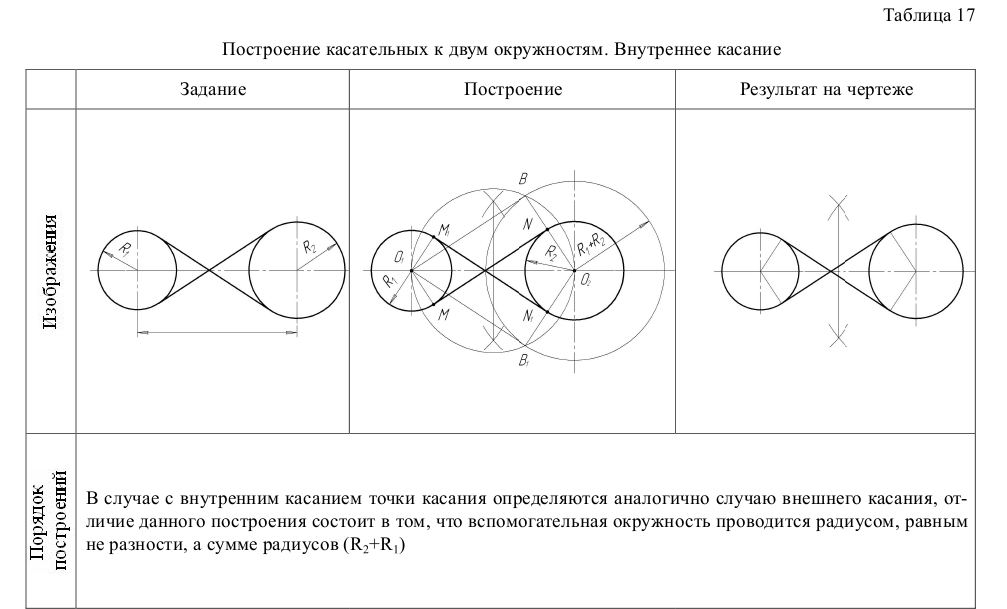
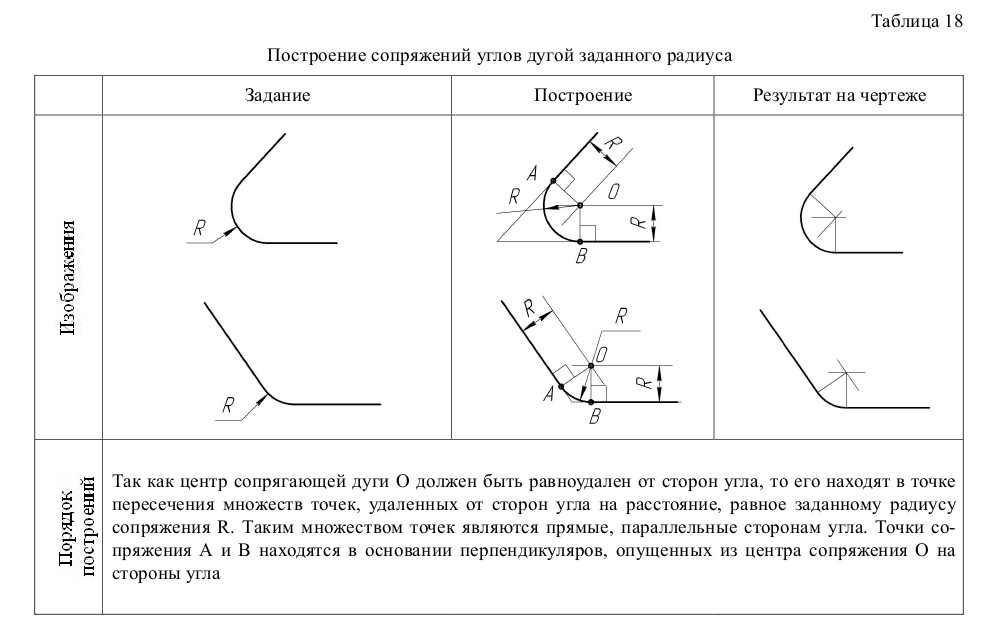
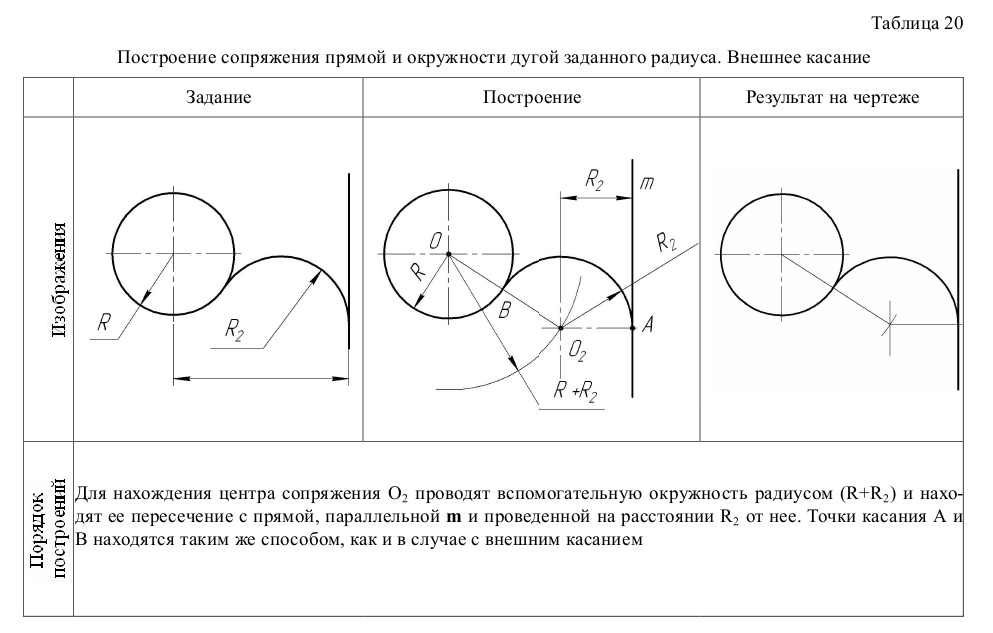
Таблица 15

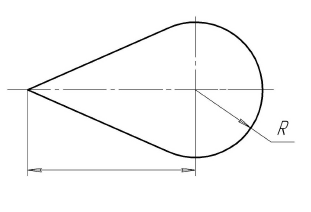
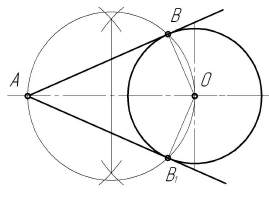
Построение касательных из точки к окружности

Задание

Построение

Результат на чертеже

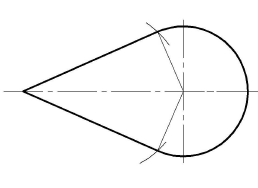
Порядок построений

Для проведения касательной из точки А к окружности соединяем точку А с центром окружности О. Приняв отрезок ОА за диаметр, строим вспомогательную окружность. Точки 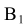и В, полученные на пересечении вспомогательной окружности с заданной, являются искомыми точками касания, так как углы А О и АВО как опирающиеся на диаметр равны 90°. Таким образом удовлетворяется условие: радиус, проведенный в точку касания, перпендикулярен касательной к окружности

Таблица 16

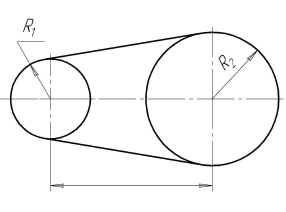
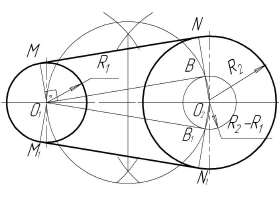
Построение касательных к двум окружностям. Внешнее касание

Задание

Построение

Результат на чертеже

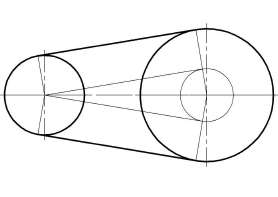
Порядок построений

Из центра 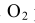радиусом, равным разности радиусов заданных окружностей ( 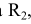-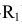), проводим вспомогательную окружность и строим к ней касательную из центра 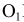способом, указанным в табл. 11. К полученным точкам касания В и 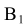проводим из центра 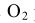радиусы и, продолжив их до пересечения с окружностью радиуса 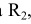, получаем точки касания N и 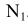. Проводя линии 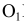М параллельно 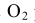N и 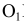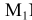параллельно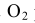 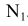, получим точки касания с окружностью радиуса 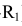. Прямые MN и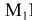 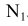являются касательными к двум данным окружностям

Таблица 17

Построение касательных к двум окружностям. Внутреннее касание

Задание

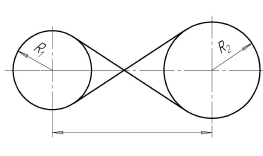
Построение

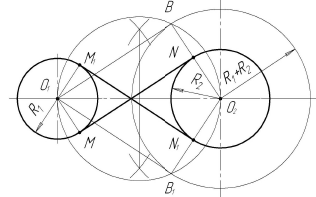
Результат на чертеже

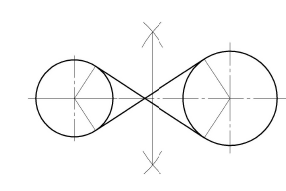
Порядок построений

В случае с внутренним касанием точки касания определяются аналогично случаю внешнего касания, отличие данного построения состоит в том, что вспомогательная окружность проводится радиусом, равным не разности, а сумме радиусов ()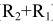

Таблица 18

Построение сопряжений углов дугой заданного радиуса

Задание

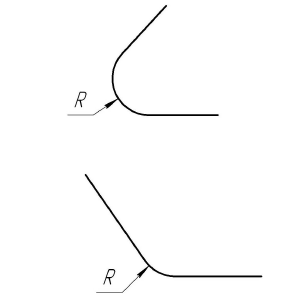
Построение

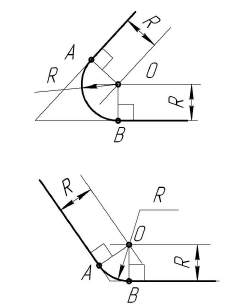
Результат на чертеже

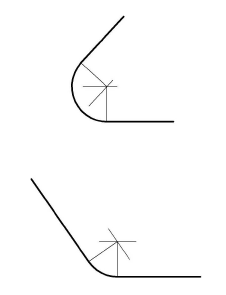
Порядок построений

Так как центр сопрягающей дуги О должен быть равноудален от сторон угла, то его находят в точке пересечения множеств точек, удаленных от сторон угла на расстояние, равное заданному радиусу сопряжения R. Таким множеством точек являются прямые, параллельные сторонам угла. Точки сопряжения А и В находятся в основании перпендикуляров, опущенных из центра сопряжения О на стороны угла

Таблица 19

Построение сопряжения прямой и окружности дугой заданного радиуса. Внутреннее касание

Задание

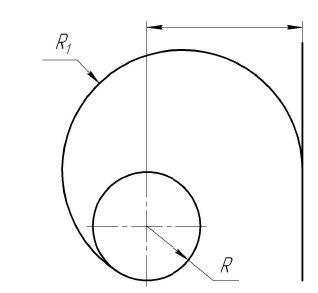
Построение

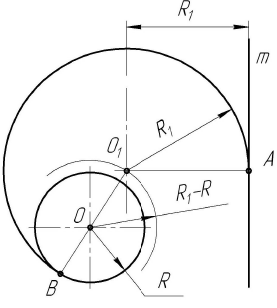
Результат на чертеже

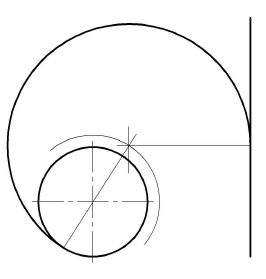
Порядок построений

Центр сопряжения находится на пересечении множеств точек, удаленных от окружности с радиусом R и от прямой на расстояние, равное радиусу дуги сопряжения. Чтобы найти центр сопряжения 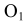, поводят вспомогательную окружность радиусом ( 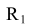-R) из центра О и прямую, параллельную заданной прямой m, на расстоянии 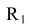от нее. Центр сопряжения 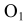находится в точке пересечения этих линий. Точка сопряжения А лежит в основании перпендикуляра, опущенного из центра сопряжения на прямую m. Точка сопряжения В находится на пересечении линии, соединяющей центры О и 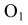, с дугой окружности радиуса R

Таблица 20

Построение сопряжения прямой и окружности дугой заданного радиуса. Внешнее касание

Задание

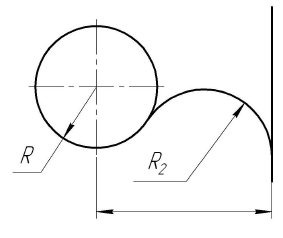
Построение

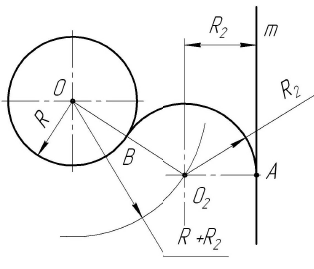
Результат на чертеже

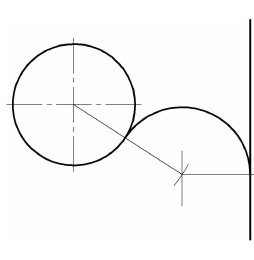
Порядок построений

Для нахождения центра сопряжения 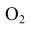проводят вспомогательную окружность радиусом (R+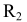) и находят ее пересечение с прямой, параллельной m и проведенной на расстоянии 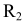от нее. Точки касания А и В находятся таким же способом, как и в случае с внешним касанием

Таблица 21

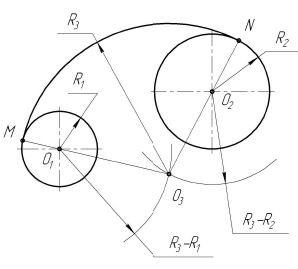
Построение сопряжения двух окружностей дугой заданного радиуса. Внутреннее касание

Задание

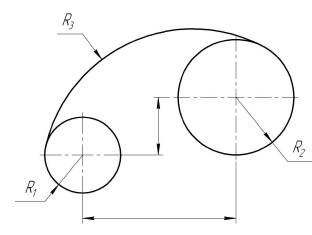
Построение

Результат на чертеже

Порядок построений

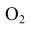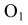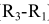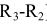Из центров и растворами циркуля, равными разности радиусов сопряжения и радиусов сопрягаемых окружностей, т. е. () и (), проводятся вспомогательные дуги. На пересечении вспомогательных дуг расположен центр сопряжения – точка 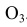. Точки сопряжения M и N находятся на пересечении заданных окружностей с прямым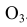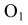и и 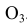соединяющими центры этих окружностей с центром сопряжения

Таблица 22

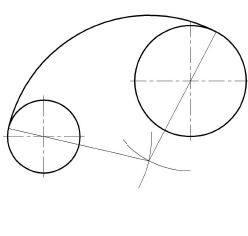
Построение сопряжения двух окружностей дугой заданного радиуса. Внешнее касание

Задание

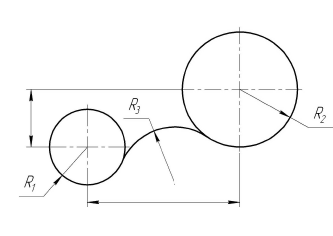
Построение

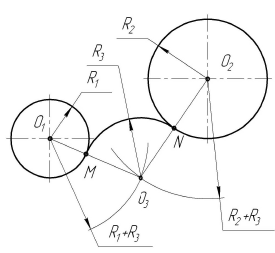
Результат на чертеже

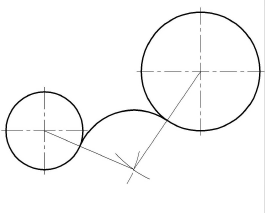
Порядок построений

Выполняются те же построения, что и для внутреннего касания, но радиусы вспомогательных дуг выбирают равными сумме радиусов заданной дуги и сопрягаемых окружностей, т. е. (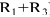) и ()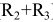

Таблица 23

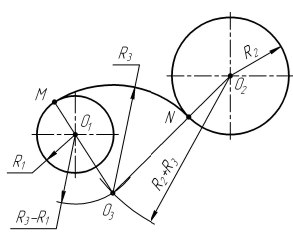
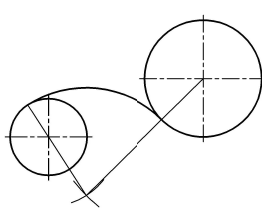
Построение сопряжения двух окружностей дугой заданного радиуса. Смешанное касание

Задание

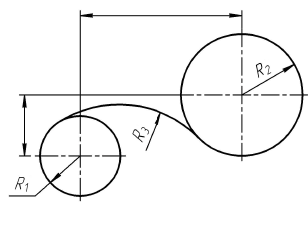
Построение

Результат на чертеже

Порядок построений

Из центра 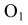раствором циркуля равным разности радиуса сопряжения 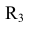и радиуса сопрягаемой окружности 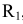, т. е. ( 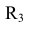-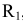), и из центра 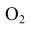раствором циркуля равным сумме радиуса сопряжения 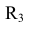и радиуса сопрягаемой окружности 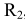, т. е. (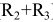), проводятся вспомогательные дуги. На пересечении вспомогательных дуг расположен центр сопряжения – точка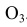. Точки сопряжения M и N находятся на пересечении заданных окружностей с прямым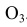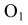и и 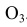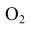, соединяющими центры этих окружностей с центром сопряжения

Геометрические построения, часто применяемые при выполнении чертежей

Проведение перпендикуляра из данной точки к прямой. Из данной точки С (рис. 2.1, а) проводим дугу окружности произвольного радиуса R так, чтобы она пересекала прямую а, получаем точки А и В. Из этих точек описываем две дуги окружности радиусом 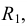несколько большим половины отрезка АВ, до пересечения в точке F. Точки F и С соединяем прямой, которая и будет искомым перпендикуляром к АВ. 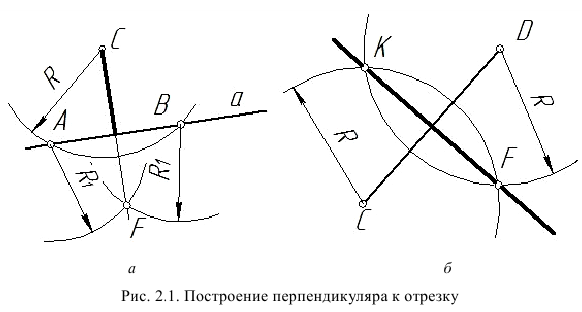Проведение серединного перпендикуляра к отрезку. Из двух концов отрезка CD (рис. 2.1, 6) (как из центров) строим две дуги окружности радиусом R, несколько большим половины отрезка CD, до пересечения в точках FK. Точки F и К соединяем прямой, которая и будет искомым перпендикуляром к CD.

Деление отрезка прямой линии на любое число равных частей. Пусть отрезок АВ требуется разделить на К) равных частей. Для этого из любого конца отрезка (из точки А) проводим под острым углом к отрезку прямую линию (рис. 2.2), на которой от точки А измерительным циркулем откладываем К) равных отрезков (точки деления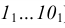) произвольной длины. Точку 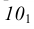соединяем с концом А данного отрезка прямой линией. Из точек делений 1-9 проводят ряд прямых, параллельных отрезку прямой 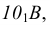которые и разделяют отрезок АВ на К) равных частей.

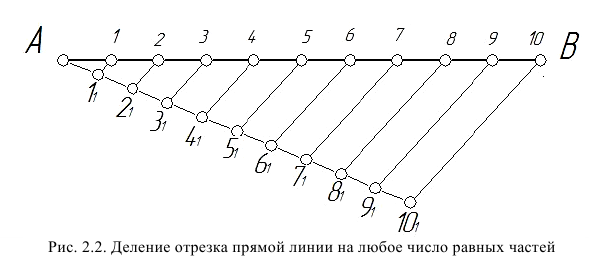
Деление угла на две равные части. Для того чтобы разделить угол ВАС (рис. 2.3, а) пополам или провести биссектрису этого угла, из вершины А строим дугу окружности произвольного радиуса R до пересечения со сторонами угла ВАС в точках У и 2. Из полученных точек проводим две дуги радиусом 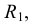несколько большим половины длины дуги 1 2 до взаимного пересечения в точке 3. Вершину угла А соединяем с точкой 3 прямой, которая делит угол ВАС пополам. Прямая АЗ - биссектриса угла АВС.

Чтобы разделить угол на четыре равные части, аналогично строим биссектрисы улов АВЗ и 3АС.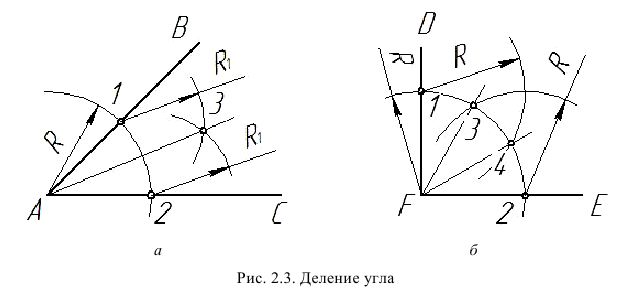

Деление прямого угла на три равные части. Из вершины F прямого угла DFE (рис. 2.3. б) произвольным радиусом R проводим дугу окружности до пересечения ее со сторонами прямого угла в точках 1 и 2, из которых проводят дуги окружности того же радиуса R до пересечения с дугой 1-2 в точках 3 и 4. Точки 1 и 2 соединяют с вершиной угла F прямыми линиями и получают стороны F3 и F4 углов DF1, 3F4 и 4FE, равных 1/3 прямого угла, т. е. 30°.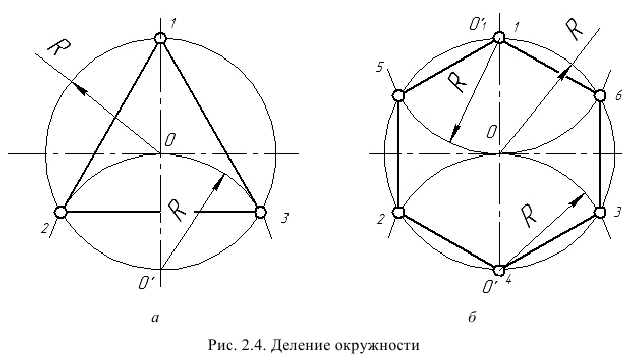

Деление окружности на три и шесть равных частей. Для того чтобы разделить окружность на три равные части, ножку циркуля ставят в точку О ’ окружности (рис. 2.4, а) и радиусом R, равным радиусу окружности, проводим дугу до пересечения с исходной окружностью в точках 2 и 3. Соединив последовательно точки 1, 2 и 3, получим вписанный в окружность правильный треугольник.

Для деления окружности циркулем на шесть равных частей применяется тот же прием, что и для деления окружности на три равные части. Радиусом окружности R (рис. 2. 4, 6) дугу описывают нс один, а два раза из точек О’ и 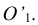Соединив последовательно точки 1, 5, 2, 4, 3 и б, получим вписанный в окружность правильный шестиугольник.

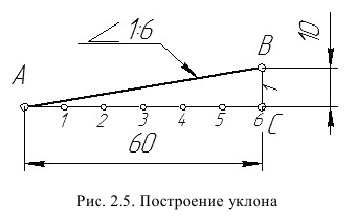
Построение уклона. Уклоном п называется отношение катета ВС, противолежащего углу а, к прилежащему катету АС (рис. 2.5), или tg а.

Уклоны выражаются в виде отношения

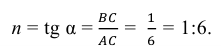Для построения прямой АВ с заданной величиной уклона к горизонтальной прямой, например 1:6, необходимо от точки С влево отложить отрезок СА, равный шести единицам длины (например 60 мм), и от точки С вверх - отрезок СВ, равный единице длины (10 мм). Точки А и В соединяем прямой, которая дает направление линии искомого уклона.

Построение конусности. Конусностью k называется отношение диаметра окружности основания конуса к его высоте. Если конус усеченный (рис. 2.6) с диаметрами оснований D и d и высотой h, то конусность определяется в виде отношения по формуле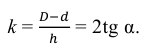

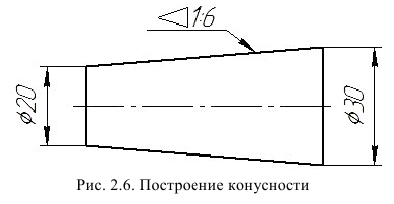
На рис. 2.6 даны размеры D = 30 мм, d = 20 мм и h = 60 мм, тогда

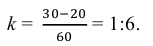В табл. 2.1 приведены значения конусности и углы конусов и уклонов, регламентируемые ГОСТом 8593-81.

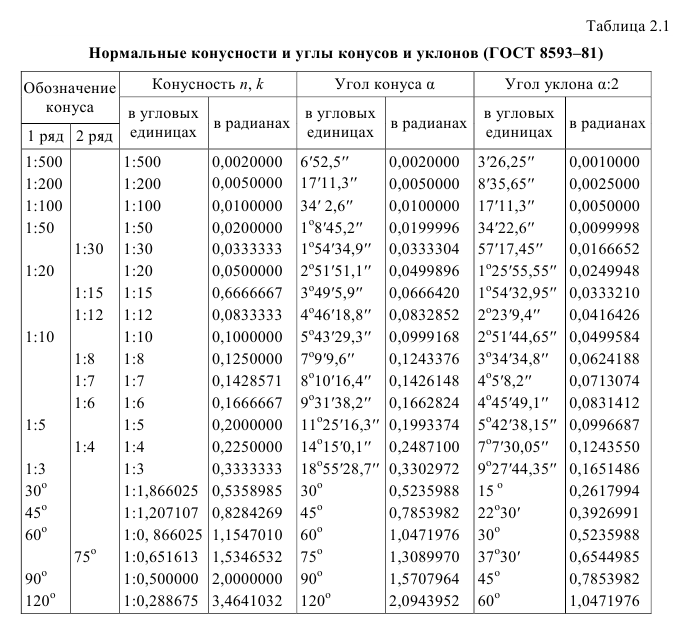
Примечание. Значение конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице.

Сопряжения линий

В основном контур очертания деталей состоит из прямых линий и дуг окружностей, плавно переходящих от одной линии к другой, такой плавный переход называется сопряжениям.

Построение сопряжений основано на двух положениях геометрии.

Первое - для сопряжения прямой линии и дуги окружности необходимо, чтобы центр окружности, которой принадлежат дуги, лежал на восстановленном из точки сопряжения перпендикуляре к заданной прямой (рис. 2.7, а).

Второе - для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, которая проходит через точку сопряжения и является перпендикуляром к общей касательной этих дуг (рис. 2.7, 6).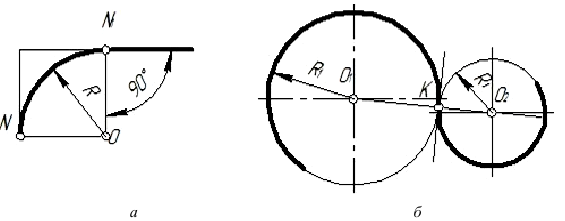

Рис. 2.7. Сопряжение прямой линии и дуги окружности (я), двух дуг (б) При вычерчивании сопряжений между двумя прямыми, прямой и окружностью, двумя окружностями при помощи некоторой дуги построение выполняется по следующему алгоритму: задав радиус дуги перехода, построением получаем центр дуги перехода и точку сопряжения.

Сопряжение двух прямых, расположенных под прямым (рис. 2.8, д), острым (рис. 2,8, 6) и тупым (рис. 2.8, в) углами дугой окружности радиуса R, выполняем следующим образом. Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводим две вспомогательные прямые линии и находим точку О пересечения этих прямых. Точка О является центром дуги радиуса R, сопрягающей стороны угла. Из центра О опускаем перпендикуляры к заданным прямым, N и 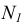- основания перпендикуляров. Из центра О между точками сопряжений N и 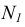строим дугу, плавно переходящую в прямые - стороны угла.

Сопряжение дуги окружности радиуса R с прямой линией дугой радиуса r (или 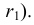Строим дугу окружности радиуса R (рис, 2.9, а) и прямую АВ. Параллельно заданной прямой на расстоянии, равном радиусу r сопрягающей дуги, проводим прямую а. Из центра О проводим дугу окружности радиусом, равным сумме радиусов R и r до пересечения ее с прямой а в точке 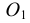. Точка 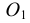является центром дуги сопряжения.

Точку сопряжения 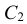находят на пересечении прямой 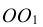с дугой окружности радиуса R. Точка сопряжения 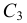служит основанием перпендикуляра, опущенного из центра 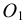на данную прямую АВ.

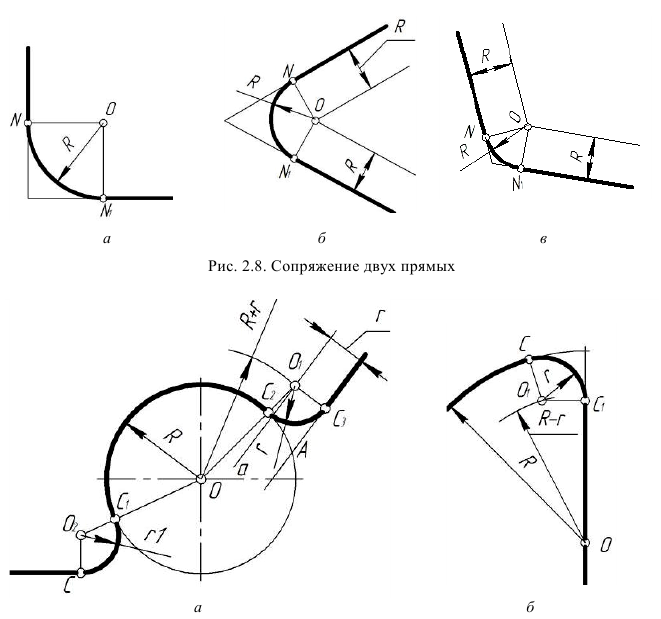
Рис. 2.9. Сопряжение дуги окружности радиуса R с прямой линией дугой радиуса r (а), сопряжение прямой, проходящей через точку О, с дугой окружности радиуса R (б) Сопряжение прямой, проходящей через точку О, с дугой окружности радиуса R (рис. 2.9, 6). Дуга сопряжения имеет радиус r. Центр дуги сопряжения 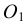находим на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии радиуса r с дугой вспомогательной окружности, описанной из точки О радиусом, равным R + r. Точка сопряжения 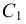является основанием перпендикуляра, опущенного из точки 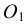на данную прямую. Точку сопряжения с находим на пересечении прямой 0 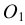с данной сопрягаемой дугой.

Сопряжение двух дуг окружностей дугой заданного радиуса может быть внешним, внутренним и смешанным.

При внутреннем сопряжении центры О и 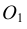сопрягаемых дуг радиусов 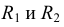лежат внутри сопрягающей дуги радиуса R (рис. 2.10).

При внешнем сопряжении центры О и 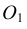сопрягаемых дуг радиусов 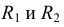лежат вне сопрягающей дуги радиуса R (рис. 2.11).

При смешанном сопряжении центр 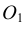одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О другой сопрягаемой дуги - вне ее (рис. 2.12).

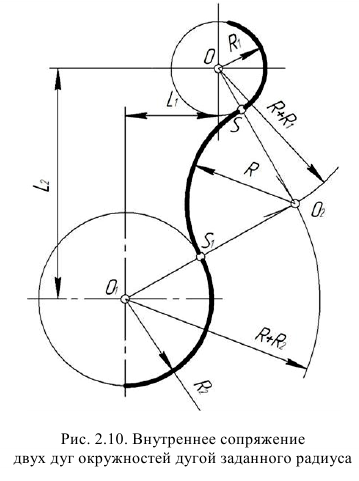
Внутреннее сопряжение двух дуг окружностей дугой заданного радиуса.

По заданным расстояниям между центрами 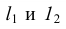(рис. 2.10) находим точки О и 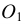, из которых проводим сопрягаемые дуги радиусов 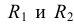. Из центра О проводим вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги 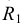и сопрягающей R 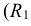+ R), а из центра 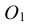проводим вспомогательную дугу радиусом, равным сумме радиусов сопрягаемой дуги 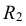и сопрягающей R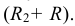. Вспомогательные дуги пересекутся в точке 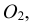которая и будет искомым центром сопрягающей дуги.

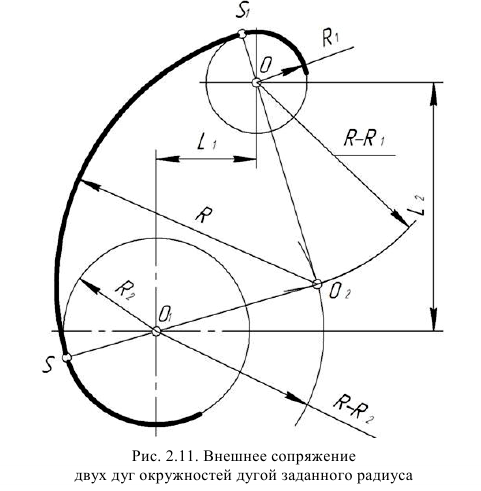
Для нахождения точек сопряжения центры дуг соединяют прямыми линиями 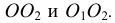Эти две прямые пересекают сопрягаемые дуги в точках сопряжения S и 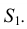Из центра 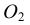радиусом R проводят сопрягающую дугу, ограничивая ее точками сопряжения S и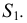

Внешнее сопряжение двух дуг окружностей дугой заданного радиуса.

По заданным расстояниям между центрами 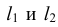(рис. 2,11) находим центры О и 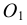, из которых проводим сопрягаемые дуги радиусов 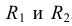. Из центра 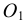проводим вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой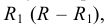а из центра О проводим вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой 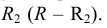Вспомогательные дуги пересекутся в точке 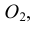которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку 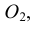соединяем с точками О и 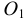прямыми линиями. Точки пересечения S и 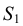- продолжения этих прямых с сопрягаемыми дугами являются искомыми точками сопряжения. Радиусом R из центра 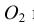проводим сопрягающую дугу между точками сопряжения S и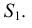

Смешанное сопряжение двух дуг окружностей дугой заданного радиуса.

По заданным расстояниям между центрами 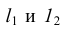(рис. 2.12) находим центры О и 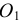, из которых проводим сопрягаемые дуги радиусов 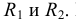Из центра О проводим вспомогательную дугу радиусом, равным сумме радиусов сопрягаемой дуги 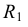и сопрягающей 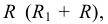а из центра 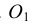проводим вспомогательную дугу радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой дуги 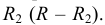Вспомогательные дуги пересекутся в точке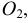которая будет искомым центром сопрягающей дуги.

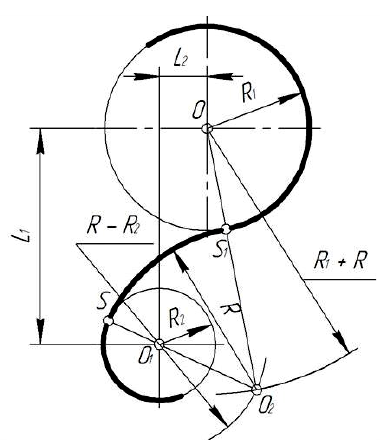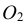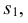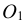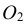Рис. 2.12. Смешанное сопряжение двух дуг окружностей дугой заданного радиуса Соединив точки О и прямой, получим точку сопряжения соединив точки и , находим точку сопряжения S.

Из центра 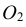проводят дугу сопряжения от S до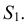

Построение касательной к двум окружностям. Из центра 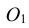проводим вспомогательную окружность радиусом R' равным разности радиусов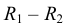(рис. 2.13) - находим 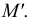точку Точку 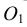соединяем с точкой 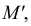на продолжении линии прямой линии 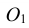М' строим точку М. Проводим параллельную линии М прямую из точки до пересечения с окружностью - находим точку N. Точки М и N - точки сопряжения.

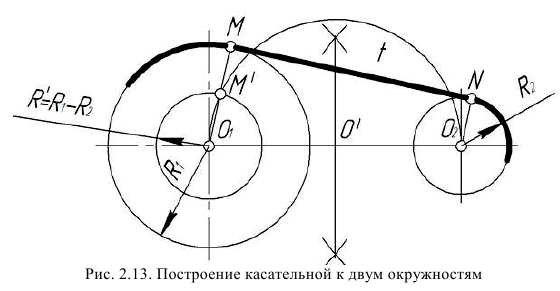
Из центра проводим вспомогательную окружность радиусом R' равным сумме радиусов 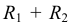(рис. 2.14) - находим 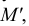точку Точку 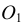соединяем с точкой 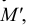на окружности радиуса находим точку М.

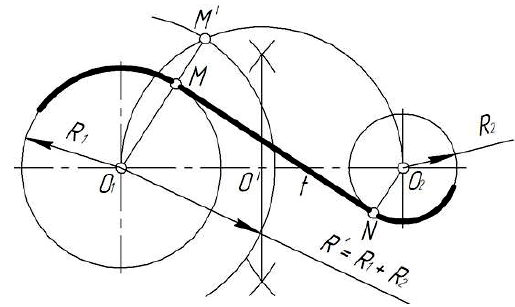Рис. 2.14. Построение касательной к двум окружностям Проводим параллельную линии М прямую из точки ()2 до пересечения с окружностью радиусом и находим точку N. Точки М и N - точки сопряжения.

Коробовые кривые

Коробовыми называются кривые, состоящие из взаимно сопрягающихся дуг окружностей различных диаметров. К таким кривым относятся овал и овоид (рис. 2.15, 2.16). 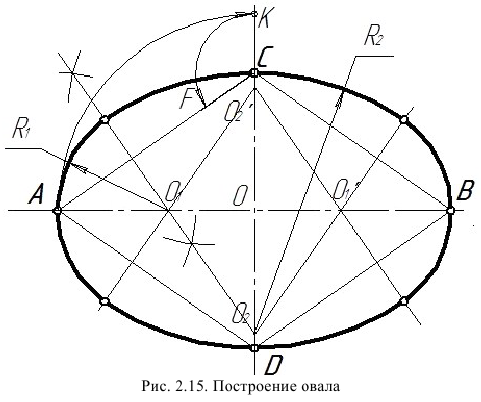Овал (рис. 2.15) представляет собой сопряжение двух дуг окружности радиуса 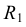с двумя дугами окружности радиуса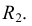

Часто при вычерчивании контуров овальных деталей, а также при выполнении их технических рисунков задаются не радиусы дуг, а величины большой и малой осей овала (рис. 2.15).

По двум перпендикулярным осям откладывают заданные длины осей овала: большой ЛВ (по горизонтали) и малой CD (по вертикали). Точки А и С - концы большой и малой осей, соединяют прямой АС. Из точки О радиусом, равным длине большой полуоси, на продолжении малой оси получаем точку К (ОА = ОК), а из точки С радиусом, равным СК, получаем на прямой АС точку F (СК = CF). К отрезку AF проводим серединный перпендикуляр (построение приведено на рис. 2.1), который пересекает большую полуось АО в точке 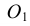и малую полуось в точке 02. Точка 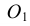является центром сопрягаемой дуги радиуса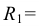 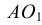, а точка 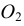- центром сопрягающей дуги радиуса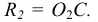

Правая половина овала вычерчивается аналогично. Овоид в отличие от овала имеет только одну ось симметрии. Радиусы R и 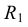дуг окружностей, центры которых лежат на оси симметрии овоида, не равны друг другу. Способ построения овоида сходен со способом построения овала.

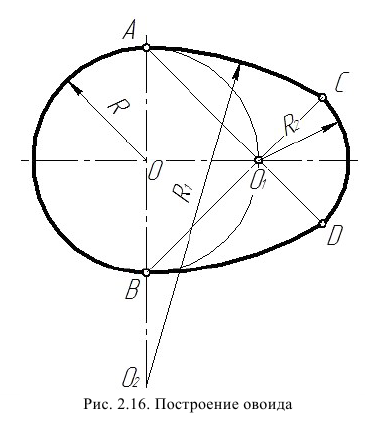
Построение овоида (рис. 2.16) по заданным величинам: радиусу R, большей сопрягаемой дуги 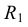, заключается в следующем. Проводим осевые линии, строим окружность данного радиуса R. Определяем точку 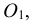являющейся точкой пересечения окружности радиуса R с осью симметрии овоида. Точки А и В соединяем с точкой 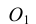. Определяем центры 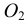заданного радиуса 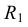и описываем дугу окружности до пересечения в точке D на продолжении прямой А. Из точки проводят третью, малую сопрягаемую дугу радиуса 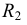овоида.

Лекальные кривые

Кривая линия (заданная множеством точек), представляющая ряд сопряженных отрезков кривых, которые невозможно построить с помощью циркуля, называется лекальной кривой.

Лекальные кривые - эллипс, парабола, гипербола, синусоида, спираль Архимеда, эвольвента, циклоидальные кривые и многие другие имеют широкое применение в технике. Например, профили зубьев цилиндрических, конических и винтовых зубчатых колес очерчивают или по эвольвенте окружности, или другим циклоидальным кривым. Особенно широко применяются в технике кривые второго порядка, к ним относятся конические сечения: окружность, эллипс, парабола и гипербола. Эти кривые являются образующими ряда поверхностей вращения (например, эллипсоида, параболоида), часто встречающихся в различных инженерных конструкциях. Поэтому необходимо изучить законы образования лекальных кривых и освоить приемы их построения.

Эллипс - замкнутая кривая, для которой сумма расстояний от любой ее точки до двух точек - фокусов эллипса, - величина постоянная, равна большой оси эллипса.

Существует множество способов построения эллипса, основанных на его свойствах, рассмотрим наиболее простой - построение эллипса по большой АВ и малой CD осям (рис. 2.17).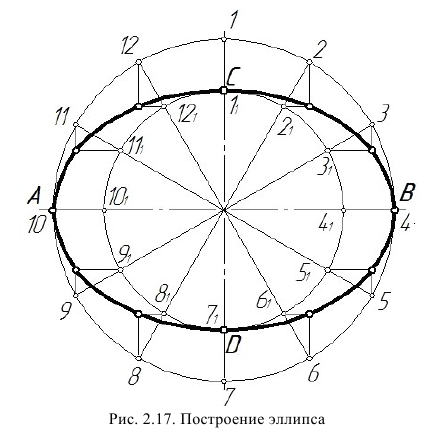

Проводим осевые линии, затем от центра О откладываем вверх и вниз по вертикальной оси отрезки ОС и OD, равные длине малой полуоси, а влево и вправо по горизонтальной оси - отрезки ОА и ОВ, равные длине большой полуоси.

Из центра О радиусами ОА и ОС проводим две концентрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводим линии, параллельные осям эллипса, до взаимного

пересечения в точках, образующих эллипс. Намеченную точками линию строим по лекалу.

Парабола - плоская кривая, каждая точка которой равноудалена от точки (фокуса), лежащей на оси симметрии и прямой (направляющей, директрисы), перпендикулярной оси симметрии.

Известно несколько способов построения параболы, рассмотрим способ построения по заданной вершине О, оси ОС и точке В (рис. 2.18).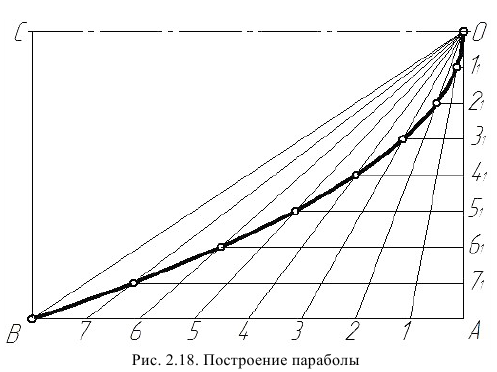

Строим вспомогательный прямоугольник ABCD. Стороны АВ и АО делим на равные части и точки деления нумеруем. Горизонтальный ряд деления (на АВ) соединяем лучами с вершиной О, а через точки деления, расположенные на АО, проводим линии, параллельные оси параболы. Точки пересечения горизонтальных прямых 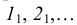с лучами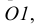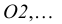принадлежат параболе. Полученные точки параболы соединяем по лекалу.

Гипербола - плоская кривая, состоящая из двух разомкнутых, симметрично расположенных ветвей (рис. 2.19), разность расстояний от каждой точки гиперболы до фокусов F и 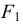есть величина постоянная и равная расстоянию между вершинами А и В.

Рассмотрим способ построения гиперболы по заданному расстоянию между вершинами АВ и фокусному расстоянию F.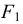

Проводим осевые линии, затем от центра О, разделив расстояние между вершинами АВ и фокусное расстояние F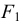 пополам, откладываем влево и вправо по горизонтальной оси отрезки О А и ОБ и отрезки OF и O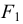. Слева от фокуса F произвольно берем ряд точек 1, 2, 3, 4, ..., постепенно увеличивая расстояние между ними. Из фокуса F описываем

дугу вспомогательным радиусом R, равным, например, расстоянию от вершины В до точки 3. Из фокуса 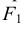проводим вторую вспомогательную дугу радиусом R|, равным расстоянию от вершины А до точки 3. На пересечении этих дуг находим точки С и 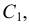принадлежащие гиперболе. Аналогично строим остальные точки правой ветви гиперболы.

Левую ветвь гиперболы строим аналогично.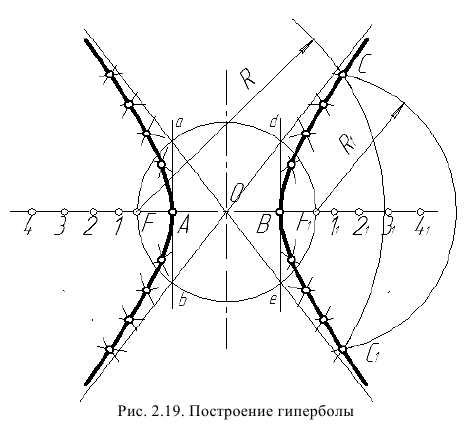

Синусоида - плоская кривая, выражающая закон изменения синуса в зависимости от величины центрального угла. Длина волны синусоиды равна 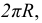где R - амплитуда синусоиды.

Для построения синусоиды по заданной амплитуде (рис. 2.20) проводим горизонтальную ось, откладываем на ней отрезок ЛВ, равный вычисленной длине волны, как 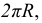и делим его на 12 равных отрезков. Слева на этой оси вычерчиваем окружность радиусом R и также делим ее на 12 равных отрезков. Точки деления нумеруем и через них проводим горизонтальные прямые. Из точек деления отрезка АВ восстанавливаем перпендикуляры к оси синусоиды и на их пересечении с горизонтальными прямыми находим точки синусоиды, которые соединяем по лекалу.

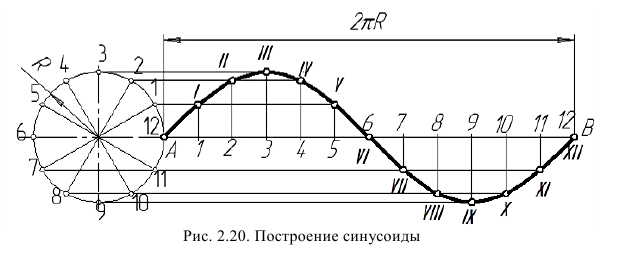
Эвольвента окружности - плоская кривая линия, являющаяся траекторией точки прямой линии, когда эта прямая перекатывается без скольжения по окружности.

Для построения эвольвенты (рис. 2.21) заданную окружность диаметра D делим на несколько равных частей, удобно на 12, которые нумеруем. Из точки 12 (последней) проводим касательную к окружности и на ней откладываем длину окружности, равную nD, которую также делим на 12 равных частей. Из точек деления окружности проводим касательные и откладываем на них соответствующие длины окружностей, а именно откладываем на первой касательной одно деление окружности, на второй — два, на третьей - три и т. д. Получаем ряд точек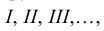, которые соединяем по лекалу.

Спираль Архимеда - это плоская кривая линия, образуемая точкой, равномерно движущейся по прямой, равномерно вращающейся вокруг неподвижной точки.

Для построения спирали Архимеда задается шаг спирали S (рис. 2.22).

Из центра О проводим окружность, равную шагу S, и делим окружность и шаг на несколько равных частей. Точки обозначаем. Из центра О, радиусом О1, 02 и т. д., проводим дуги до пересечения с соответствующими радиусами. Полученные точки 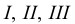и т. д., принадлежащие спирали, соединяем по лекалу плавной кривой линией.

Циклоида - плоская кривая линия, являющаяся траекторией точки, лежащей на окружности, которая катится без скольжения по прямой.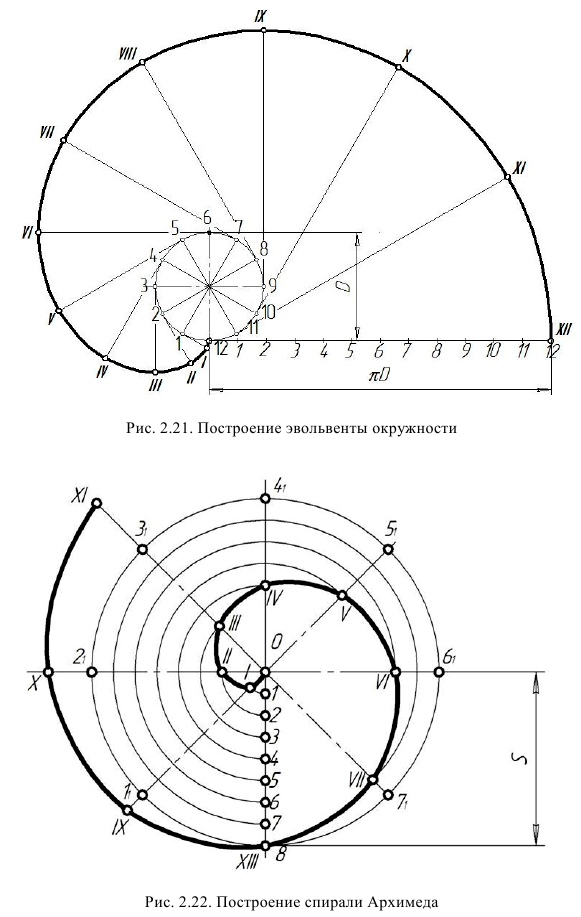

Построение циклоиды. На направляющей горизонтальной прямой (рис. 2.23) откладываем длину производящей окружности радиусом R,равную 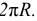Окружность и отрезок делят на несколько равных частей, удобно на 12. Из точек делений отрезка /, 2,5, 412 восстанавливаем перпендикуляры до пересечения с продолжением горизонтальной оси окружности, получаем точки 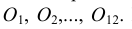Из точек делений окружности проводим горизонтальные прямые, на которых из точек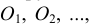 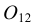делаем засечки дугами окружности радиуса R и получаем точки, принадлежащие циклоиде, которые соединяем по лекалу плавной кривой линией.

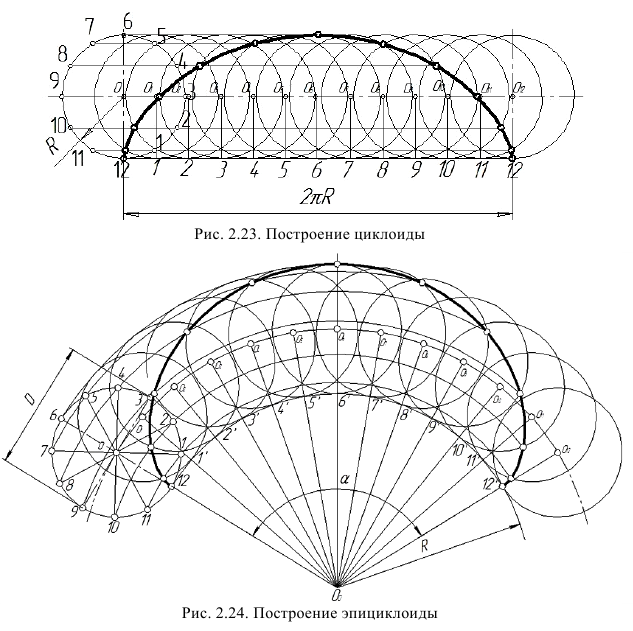
Эпициклоида - это плоская кривая линия, являющаяся траекторией точки, лежащей на окружности, которая катится без скольжения по направляющей окружности.

Построение эпициклоиды. Производящую окружность диаметра D и направляющую окружность радиуса R проводим так, чтобы они касались в точке 12 (рис. 2.24). Производящую окружность делим на 12 равных частей. Из центра 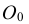радиусом, равным R + 0,5D, проводим вспомогательную дугу.

Центральный угол а определяют по формуле

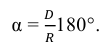
Разделив дугу направляющей окружности, ограниченную углом а, на 12 равных частей, получаем точки 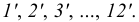Из центра 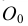через точки 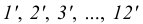проводим прямые, которые продолжают до пересечения с вспомогательной дугой в точках 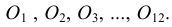Из центра 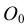проводим вспомогательные дуги через точки делений 1-12 производящей окружности.

Из точек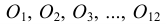(как из центров) проводим окружности диаметром D до пересечения с вспомогательными дугами и получаем точки пересечения, принадлежащие эпициклоиде. Полученные точки соединяем по лекалу.

Кстати вы всегда можете заказать чертежи.

Лекции по предметам:

1. Инженерная графика
2. Начертательная геометрия
3. Компас
4. Автокад
5. Черчение
6. Проекционное черчение
7. Аксонометрическое черчение
8. Строительное черчение
9. Техническое черчение