Геометрические задачи и методы их решения с примерами

Содержание:

Логическое построение геометрии

Геометрия - это наука о пространственной форме и количественных характеристиках предметов реального мира. Прочие свойства предметов изучают другие дисциплины. Если при изучении предмета учитывать только пространственную форму и размеры, то получим абстрактный объект, называемый геометрической фигурой.

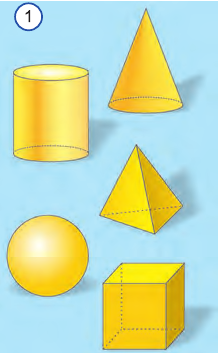
Слово "геометрия" - греческого происхождения и в переводе означает землеизмерение. Геометрию, изучаемую в школе, называют евклидовой по имени древнегреческого ученого Евклида. Геометрия состоит из двух частей: планиметрии и стереометрии. Планиметрия изучает свойства фигур на плоскости, а стереометрия - в пространстве (рис. 1).

Чтобы отличать геометрические фигуры друг от друга, их свойства описывают в виде утверждения, которое называют определением. Однако, определить вес геометрические фигуры невозможно. Некоторые из них, первоначальные, вынуждены принять без определения. Принимаем их за неопределяемые, начальные (основные) геометрические фигуры. Логическое построение геометрии осуществляют в следующем порядке: 1. Вначале принимают основные (начальные) геометрические фигуры без определения; 2. Принимают основные свойства этих фигур без доказательств;

3. Определяют другие геометрические фигуры через основные фигуры и их свойства, а затем доказывают свойства этих фигур и утверждений, истинность которых устанавливается путем доказательств, опираясь на известные.

Такое построение науки называют аксиоматическим построением. Свойства фигур, принятые без доказательства, называют аксиомами.

В планиметрии, которую мы изучали до сих пор основными геометрическими фигурами были точка и прямая. Их приняли без определения. Но определили отрезок, луч, треугольник и другие геометрические фигуры. Точно так же следующие свойства (утверждения) мы принимаем без доказательств в качестве аксиом:

I. Аксиомы принадлежности

1.1. Какова бы ни была прямая на плоскости, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

1.2. Через любые две точки можно провести прямую, и притом только одну.

II. Аксиомы расположения

2.1. Из трех точек, лежащих на прямой, одна и только одна лежит между двумя другими.

2.2. Любая прямая делит плоскость на две части: на две полуплоскости.

III. Аксиомы измерения

3.1. Любой отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

3.2. Любой угол имеет определенную градусную меру, большую нуля. Градусная мера развернутого угла равна 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

IV. Аксиомы откладывания

4.1. На любом луче от его начальной точки можно отложить единственный отрезок, равный данному.

4.2. От любого луча в определенную полуплоскость можно отложить единственный угол, равный данному, не развернутому углу.

4.3. Для любого треугольника существует единственный равный ему треугольник в заданном расположении относительно данного луча.

V. Аксиома параллельности

5.1. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Вывод некоторого утверждения с помощью логических размышлений называют доказательством. Утверждение, верность которого установлена с помощью доказательства, называют теоремой. Обычно теорема состоит из условия и заключения. В первой части теоремы - условии объясняют что задано. А во второй части - заключении формулируют что требуется доказать.

Доказать теорему - эго значит, используя ее условие, опираясь на принятые и доказанные ранее свойства, рассуждая, привести к правильности предложения, сформулированного в заключении.

Уточнение условия и заключения теоремы - разъясняет ее, облегчает понимание и доказательство теоремы.

Древнегреческий ученый Платон отмстил удивительную закономерность в геометрии: из свойств, изученных и доказанных ранее, логически размышляя и обдумывая, можно получить новые свойства. Следовательно, используя эти удивительные возможности, можно формулировать остальные свойства в виде теорем, которые доказывают с помощью логических размышлений, аксиом, а также свойств, доказанных до этого.

В процессе размышления запрещается использование недоказанных свойств, даже если их правильность очевидна.

Таким образом, если рассматривать геометрию как одно здание, начальные понятия и аксиомы составляют его фундамент. Кирпичи, уложенные на этом фундаменте - это новые определяемые понятия и свойства, доказанные в виде теорем.

В формировании геометрии в качестве самостоятельной науки большой вклад внесли древнегреческие ученые. Например, Гиппократ Хиосский дал разъяснения о первых геометрических понятиях. Наибольший вклад в этой области принадлежит великому древнегречеcкому ученому Евклиду (356-300 годы до нашей эры). Его основной труд "Начала" содержит планиметрию, стереометрию и некоторые вопросы теории вероятностей, кроме того, алгебру, основы теории отношений, способы вычисления площадей и объемов и также элементы теории пределов. Евклид в "Началах" собрал все достижения древнегреческих математиков того времени и создал основу для дальнейшего развития математики.

"Начала" состоят из 13 книг и содержат переработанные труды древнегреческих ученых V - IV веков до нашей эры. В нем приведены 23 определения, 5 постулатов и 9 аксиом. В этом труде даны правильные определения прямоугольника, квадрата и окружности. Для точки и прямой приведены следующие определения: "Точка-это то, что не имеет частей", "Линия-это длина без ширины".

В "Началах" приведены 9 аксиом - высказывания, принятые без доказательства. Также приведены следующие 5 математических умозаключений (постулатов), позволяющие осуществлять геометрические построения:

I. Через любые две точки можно провести только одну прямую.

II. Отрезок прямой можно бесконечно продолжить.

III. Из любой точки можно построить окружность произвольныго радиуса.

IV. Все прямые углы равны между собой.

V. Если две прямые, лежащие в одной плоскости, пересеченные третьей, образуют внутренние углы, сумма которых меньше двух прямых углов, то при продолжении вышеупомянутых прямых они пересекутся с той стороны, где сумма углов меньше двух прямых углов.

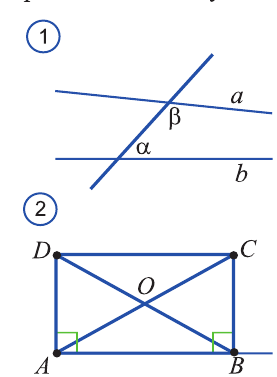
Упомянутый труд получил огромную славу и признание. Особенно V постулат стал причиной большой научной дискуссии. Если обозначить внутренние углы в V постулате а и (3 (рис. 1), а прямые а и b, то по смыслу этого постулата а+(3 <180°, и прямые аи b пересекаются.

Многие ученые, пытаясь доказать постулат V, заменяли его другими равносильными умозаключениями. Например, аксиома параллельных английского математика Яна Плейфер (1748-1819) звучит так: На плоскости из точки, расположенной вне прямой, можно провести только одну прямую, параллельную этой прямой.

Математик, поэт, астроном и философ Омар Гиясаддин Лбул Фахт ибн Ибрахим Хайям также занимался этой задачей. Хайям в своем сочинении "Комментарии к сложностям в вводной части книги Евклида" остановился на V постулате. Он, пытаясь доказать постулат Евклида как теорему, рассмотрел прямоугольник с двумя прямыми углами в основании и сделал вывод, что, если два угла при нижнем основании прямые, то и углы при верхнем основании должны быть прямыми (рис.2). Хайям говорит:

"Две прямые, перпендикулярные одной и той же прямой, не могут пересечься". Итальянский математик Д. Саккери (1667-1733), не знакомый с работой Омара Хайяма, занимаясь V постулатом, также обратился к прямоугольнику. Данный прямоугольник вошел в основания геометрии под названием "Прямоугольник Хайяма-Саккери".

Эту проблему решил великий русский математик Николай Иванович Лобачевский, построив неевклидовую геометрию. Лобачевский впервые доказал, что пятый постулат Евклидовой геометрии не связан с другими аксиомами. Эта геометрия полностью отличалась от Евклидовой геометрии. Однако, ни к каким логическим противоречиям это не привело, несмотря на то, что две геометрии не могли существовать одновременно. Несмотря на это, Лобачевский сделал новые результаты, которые также не имели логических противоречий. Новая геометрия и геометрия Евклида полностью совпадали по первым четырем аксиомам. Эта группа аксиом и их следствия назвали абсолютной геометрией.

Однако, неевклидовая геометрия (геометрия Лобачевского) серьезно отличалась от геометрии Евклида. Например, в геометрии Лобачевского сумма внутренних углов треугольника может быть меньше л, подобных, но неравных треугольников не существует, множество точек, равноудаленных от данной прямой, являются не прямой, а кривой линией и так далее.

В создание неевклидовой геометрии внесли большой вклад венгерский математик Янош Бойяи (1802-1860) и немецкий математик Карл Фридрих Гаусс (1777-1855). Также большую работу по описанию новой геометрии проделали итальянский ученый Эудженио Бельтрами (1835-1900) и немецкий математик Бернхард Риман (1826-1866).

Начатая Евклидом аксиоматика в некотором смысле получила завершение в работах немецкого математика Давида Гильберта (1862-1943) и русского математика Вениамина Федоровича Кагана (1869-1953).

• Заказать решение задач по высшей математике

Геометрические задачи и методы их решения

Как было отмечено ранее, одно из самых замечательных свойств геометрии заключается в возможности создания новых утверждений на основе ранее изученных, доказанных предложений, с помощью рассуждений и логического мышления. С помощью этой замечательной возможности доказываются и оставшиеся утверждения, выраженные в виде теорем или задач, основываясь на аксиомах и ранее доказанных свойствах. На основе этого и появлялись математические или геометрические задачи.

В математической задаче приводятся данные (условия). Используя их, требуется что-то найти (вычислить), или доказать, или построить. Выполнение поставленных требований и является решением задачи.

Геометрические задачи в соответствии с поставленным требованием делятся на вычислительные задачи, на задачи, требующие доказательства, исследовательские задачи и задачи на построение.

Для решения математической задачи знание условия недостаточно. Предполагается также наличие навыков и опыта решения задач. Чтобы добиться таких навыков нужно начать с решения простых задач и последовательно переходить к решению болсс сложных. Точно также нужно рассматривать различные методы решения и для их успешного усвоения решать много задач. Каждый метод применяется для определенной группы задач. Чем больше методов вы будете применять, тем больше получите навыков решения задач.

Ниже мы остановимся на некоторых наиболее важных методах решения геометрических задач. Методы решения задач по структуре делятся на синтетический, аналитический, доказательства от противного и другие. А но применению аппарата математики делятся на методы: алгебраический, векторный, координатный, вычисления площадей, подобия, геометрического преобразования.

Синтетический метод

Синтетический метод: используя данные условия задачи строят цепочку логических рассуждений. Цепочку продолжают до тех пор, пока ее последнее звено не совпадет с требованием задачи.

Пример:

Биссектриса прямоугольника делит его сторону на отрезки длиной 7 см и 9 см (рис. 1). Найдите периметр прямоугольника.

Решение:

Пусть ABCD- прямоугольник, А К -биссектриса,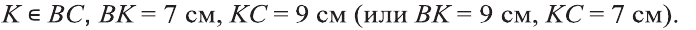

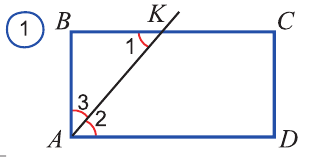
Эта задача входит в число опорных задач, так как многие задачи составляют на основании аналогичной идеи. Биссектрисы параллелограмма и трапеции отсекают от плоскости этих фигур равнобедренные треугольники. О таких важных фактах нужно помнить всегда. Они очень помогают при решении других задач.

Аналитический метод

Аналитический метод заключается в том, что, исходя из требования (вывода) утверждения (теоремы или задачи) и опираясь на известное утверждение, строится цепочка логических рассуждений, которая показывает, что требование является следствием условия.

Пример:

Докажите, что середины сторон любого четырехугольника являются вершинами параллелограмма.

Доказательство:

Пусть ABCD - четырехугольник (рис. 2), АК — КВ, BL = LC, CQ = QD, АР = PD. Проведем диагонали АС и BD четырехугольника.

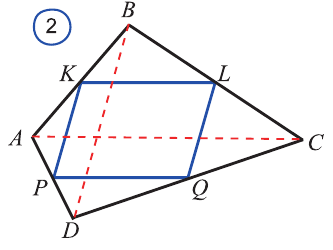
5. Из (3) и (4) имеем: KLQP - параллелограмм.

Рассмотренные выше синтетический и аналитический методы также называются прямыми методами. При решении задач прямыми способами сначала анализируется условие задачи. По результатам анализа выбирается метод, после этого строится и разбирается модель (чертеж) задачи в виде рисунка. В таком русле ведется обсуждение и переход от условия задачи к ее решению.

Есть и обратный метод решения задачи. С ним мы часто сталкивались. Называется этот метод "методом доказательства от противного". Приведем алгоритм использования этого метода.

Алгоритм применения метода доказательства от противного.

Пример:

Если каждая из двух прямых параллельна третьей, то они параллельны между собой.

Пусть заданы прямые а и b, и пусть каждая из них параллельна третьей прямой с. Докажем теорему методом доказательства от противного.

Доказательство: Предположим противное:

Пусть каждая из прямых а и Ъ параллельна третьей прямой с, но сами прямые не параллельны друг лругу, то есть они пересекаются в некоторой точке А (рис. 3). Тогда через точку А прямой с проходят две прямые а и Ъ, параллельные ей. Это противоречит аксиоме параллельности. Следовательно, предположение было неверным. Значит, если каждая из двух прямых а и b параллельна третьей прямой с, то эти прямые параллельны между собой.

Вышеприведенный метод основан на следующем логическом законе: из двух противоречащих друг другу утверждений только одно верно, а другое ложно, третьего не дано.

Теперь рассмотрим другие методы решения геометрических задач.

Алгебраический метод

При решении геометрических задач алгебраическим методом целесообразно пользоваться следующим алгоритмом:

1. проанализировать содержание задачи и построить модель его чертежа;
2. обозначить неизвестные буквами;
3. по условию задачи составить уравнение или систему уравнений;
4. решить составленные уравнения или системы уравнений;
5. проанализировать полученное решение;
6. написать ответ.

Пример:

Периметр прямоугольного треугольника равен 36 см. Отношение гипотенузы к катету равно 5 : 3. Найдите стороны треугольника.

Пусть задан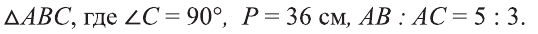

Решение:

Обозначим коэффициент пропорциональности буквой к.

Тогда АВ = 5к, АС = 3к.

По теореме Пифагора: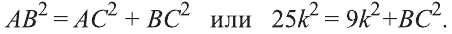

Откуда,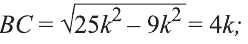

По условию задачи: Р = 36 см, Р = АВ + АС + ВС.

Следовательно, 5к + 3к + 4к = 36. Откуда, к- 3;

Тогда, АВ = 5к = 15 (см), АС =3к=9 (см), ВС = 4к=12 (см).

Ответ: 15 см, 9 см, 12 см.

Метод площадей

При решении некоторых геометрических задач применение формул вычисления площадей быстро приводит к ожидаемому результату. В этом случае требуемые в задаче неизвестные находят из уравнения, полученного в результате уравнивания площадей вспомогательных фигур. В этом случае требуемые в задаче неизвестные находят из уравнения, полученного в результате уравнивания площадей вспомогательных фигур. Продемонстрируем это на следующем примере.

Пример:

Стороны треугольника 13 см, 14 см и 15 см. Найдите высоту, которая опущена на сторону, равную 14 см.

Решение.

Пусть задан треугольник

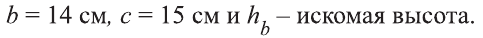
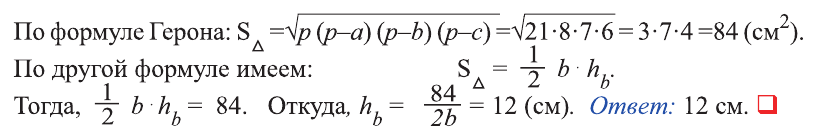
Векторный метод

При решении геометрических задач векторным методом целесообразно пользоваться следующим алгоритмом:

1. перевести задачу на язык векторов, то есть рассмотреть некоторые величины (отрезки), заданные в задаче как векторы, составить векторное равенство;
2. используя свойства действий над векторами преобразовать векторные равенства и найти неизвестное;
3. вернуть с векторного языка на геометрический;
4. записать ответ.

Метод векторов используется при решении задач, в которых требуется:

• доказать параллельность прямых (отрезков);
• поделить отрезки в заданном отношении;
• показать, что три точки лежат на одной прямой;
• показать, что четырехугольник является параллелограммом (ромбом, трапецией, квадратом, прямоугольником).

Пример:

Докажите, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма.

Решение:

Пусть ABCD заданный четырехугольник, где АК - КВ, BL - LC, CQ = QD, АР = PD (рис. 4).

Доказательство:

1. Заменив отрезки соответствующими векторами

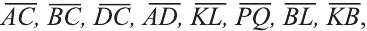, запишем задачу векторным языком;

2. Используем для сложения векторов правилом треугольника:

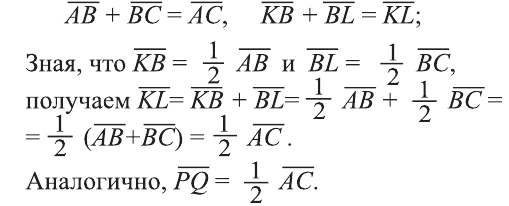
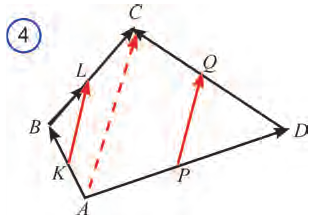
3. 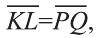то есть эти векторы одинаково направлены и их длины равны. Следовательно, по признаку параллелограмма четырехугольник KLQP является параллелограммом.

Метод координат

При решении геометрических задач методом координат целесообразно пользоваться следующим алгоритмом:

1. проанализировать содержание задачи и записать геометрическую задачу на языке координат;
2. преобразовать выражение и вычислить его значение;
3. перевести результат на геометрический язык и записать ответ.

Методом координат чаще всего решают следующие задачи: а) на нахождение геометрических мест точек; б) на доказательство зависимости между линейными элементами геометрических фигур.

При решении задач методом координат важно рационально выбрать систему координат. Данную фигуру следует разместить относительно осей координат таким образом, чтобы как можно больше координат нужных точек равнялись нулю или одному и тому числу.

Пример:

Докажи те, что параллелограмм, диагонали которого равны, является прямоугольником.

Доказательство:

Выберем систему координат так, чтобы вершины параллелограмма имели следующие координаты (рис. 5):

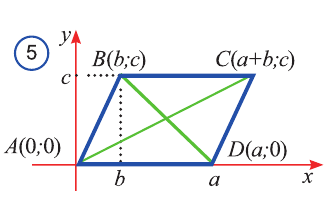
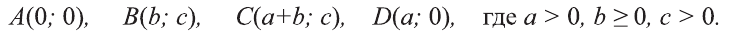
Выразим расстояния между точками А, В, С, D через их координаты: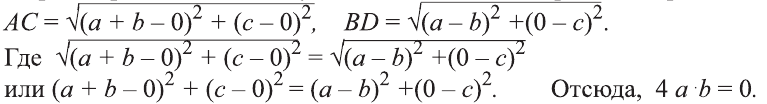

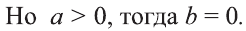
Это, в свою очередь, означает, что точка В (b; с) лежит на оси Оу. Поэтому АBСD прямоугольный.

Отсюда следует, что параллелограмм ABCD является прямоугольником.

Метод геометрических преобразований

Метод геометрических преобразований: метод поворота, метод симметрии, метод параллельного переноса и метод гомотетии. При решении задач методом геометрических преобразований наряду с данными геометрическими фигурами рассматриваются и фигуры, полученные в результате определенного преобразования. Определяются свойства новых фигур и переносятся на данную фигуру. Затем выбирается способ решения задачи.

Все приведенные выше методы, где используется больше свойств геометрических фигур, называются геометрическими методами.