Геометрические фигуры и их свойства с примерами и решением

Содержание:

Геометрия — наука о геометрических фигурах и их свойствах. Самая простая геометрическая фигура — точка. Каждая другая геометрическая фигура состоит из точек, то есть является некоторым множеством точек. Другие фигуры — прямая, плоскость. Их содержание раскрывают не определениями, а описывая их основные свойства. Фигуры, расположенные на одной плоскости, называют плоскими. Раздел геометрии, в котором изучаются фигуры на одной плоскости, называется планиметрией.

Мы начинаем изучать планиметрию — раздел геометрии, в котором рассматриваются фигуры на плоскости. Из курса математики вы уже имеете представление о некоторых из них. Наша ближайшая цель — восстановить и дополнить эти начальные знания. Геометрические сведения мы будем излагать в определенной логической последовательности, чтобы они стали прочным фундаментом для дальнейшего изучения геометрии.

Основу любой науки составляют утверждения, которые принимаются как исходные и не требуют обоснования. В математике такие утверждения называют аксиомами. Аксиомы планиметрии, которые мы рассмотрим в этой главе, выражают основные свойства простейших геометрических фигур. На их основе с помощью логических рассуждений мы будем получать более сложные геометрические факты.

Планиметрия - от латинского "планум" и греческого "метрио" - измеряю.

Определения

Основные свойства расположения точек на прямой:

• Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.
• Через любые две точки можно провести прямую, и только одну.
• Из трех точек прямой одна и только одна лежит между двумя другими.

Части прямой — отрезок и луч. Отрезок АВ — это часть прямой, содержащая точки А, В и все точки, лежащие между ними. Каждому отрезку соответствует его длина. Длина отрезка — расстояние между его концами. Расстояние и длину измеряют метрами, сантиметрами, миллиметрами, километрами, футами, дюймами и другими единичными отрезками.

Основные свойства измерения отрезков:

Каждый отрезок имеет определенную длину.

Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Часть плоскости, ограниченная двумя лучами с общим началом, называется углом. Углы бывают острые, прямые, тупые, развернутые и больше развернутого. Меры углов определяют в градусах, минутах, секундах, румбах и некоторых других единицах измерения.

Основные свойства измерения углов:

Каждый угол имеет определенную меру.

Мера угла равна сумме мер углов, на которые данный угол делится его внутренним лучом.

Биссектриса угла — внутренний луч, разбивающий данный угол на два равных угла.

Точки и прямые

Геометрия — это наука о геометрических фигурах и их свойствах. Самая простая геометрическая фигура — точка. Любая другая геометрическая фигура состоит из точек. Например, окружность — это фигура, состоящая из всех точек плоскости, равноудаленных от данной точки (рис. 1).

Отрезок также состоит из точек. Любое множество точек является геометрической фигурой. Часть геометрической фигуры или объединение нескольких фигур — тоже геометрическая фигура (рис. 2).

Одна из геометрических фигур — плоскость. Представление о части плоскости дает поверхность стола, потолка, пола. В геометрии плоскость считается неограниченной, идеально ровной и гладкой.

Фигуры, расположенные на одной плоскости, называют плоскими. Все вышеназванные геометрические фигуры — плоские. А куб, шар, прямоугольный параллелепипед — неплоские фигуры (рис. 3). Раздел геометрии, в котором изучаются фигуры на одной плоскости, называется планиметрией (латинское planum — плоскость).

Мы начинаем изучать планиметрию. Прежде всего рассмотрим, как могут быть расположены на плоскости  точки    и    прямые.

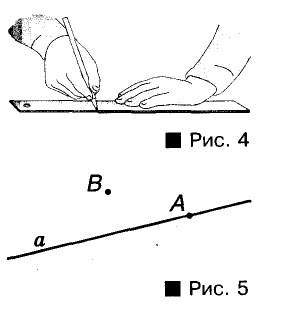
Вы уже знаете, как с помощью линейки проводят прямые (рис. 4).

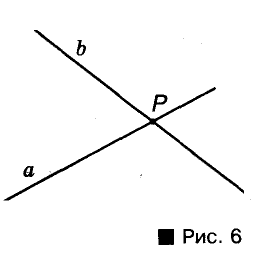
Прямая в геометрии — идеально ровная и бесконечная в обе стороны. Кик и любая другая фигура, прямая состоит из точек. Если точка А лежит на прямой а, говорят, что прямая а проходит через точку А. Записывают так: А е а. Если точка В не лежит на прямой а, пишут: 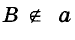(рис. 5).

Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.

Через одну точку можно провести много прямых. На рисунке 6 вы видите прямые а и Ь, проходящие через точку Р. Это их общая точка, других общих точек прямые а и Ъ не имеют. Если две прямые имеют только одну общую точку, говорят, что они пересекаются в этой точке. Прямые а и b Пересекаются в точке Р.

Если прямой принадлежат точки А и В, говорят, что эта прямая проходит через точки А и В. Обозначают ее так: АВ.

Через любые две точки можно провести прямую, и только одну.

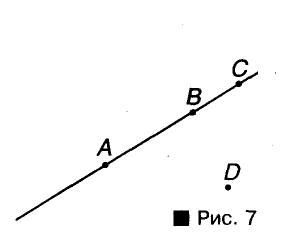
Можно ли провести прямую через три точки? Не всегда. Если точки А, B и C расположены, как показано на риcунке 7, через них прямую провести можно. А через точки А, В и D — нельзя. Говорят, что точки А, В и D Не лежат на одной прямой. Точки А, В, (- лежат на одной прямой, причем В — между А и С.

Простейшие геометрические фигуры и их свойства

Из трех точек прямой одна и только одна лежит между двумя другими.

Если точка В лежит между А и С, говорят, что точки А и С лежат по разные стороны от В, а точки А и В — по одну сторону от С.

Напечатанные выше жирным шрифтом три предложения со значком — это основные свойства расположения точек на прямой.

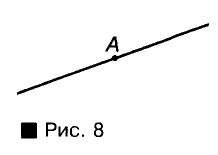
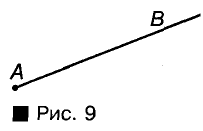
Любая точка А прямой делит эту прямую на две части (рис. 8). Каждую из частей прямой вместе с точкой А называют лучом, выходящим из точки А. Точку А называют началом луча. Если говорят «луч АВ», то имеют в виду, что начало луча находится в точке А (рис. 9).

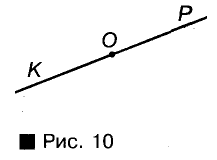
Два луча, имеющие общее начало и дополняющие друг друга до прямой, называются дополнительными. На рисунке 10 вы видите луч ОК — дополнительный для луча ОР и луч ОР — дополнительный для ОК.

 

Геометрия — часть математики (рис. 11). Геометрическая наука богата содержанием и методами  исследования. Она включает элементарную геометрию, высшую геометрию, неевклидовы геометрии, топологию и др. В школе изучают только элементарную геометрию.

Геометрия тесно связана со многими другими науками, прежде всего с физикой. Но физика занимается изучением материальных тел (имеющих массу, температуру, цвет и т. п.), а в геометрии абстрагируются от всего материального. Абстрагироваться — означает мысленно отвлечься от конкретных объектов, окружающих нас. Абстрагируясь от материальных вещей, мы в воображении создаем идеальные объекты по сходным свойствам. Конец иголки, натянутая струна — это материальные объекты. Они имеют определенную толщину, длину, массу. Абстрагируясь от таких физических свойств, человеческое воображение создало абстрактные геометрические понятия точка, прямая. В природе абстрактной прямой нет, но это понятие существует в человеческом воображении. И очень полезное понятие, поскольку все свойства прямой и ее частей, выявленные в геометрии, переносятся на миллионы и миллиарды всех натянутых струн, прямолинейных рельсов, труб, лент и т. п. Не существует в природе и плоскость без толщины, идеально ровная и гладкая, бесконечная в каждом ее направлении. Но для науки это идеальное понятие очень важно, поскольку свойства, установленные в геометрии для плоскости и ее частей, можно переносить на свойства миллиардов конкретных стен, оконных стекол и других предметов, имеющих плоские поверхности.

Пример №1

На сколько частей могут разбивать плоскость три ее прямые?

Решение:

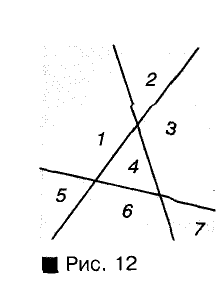
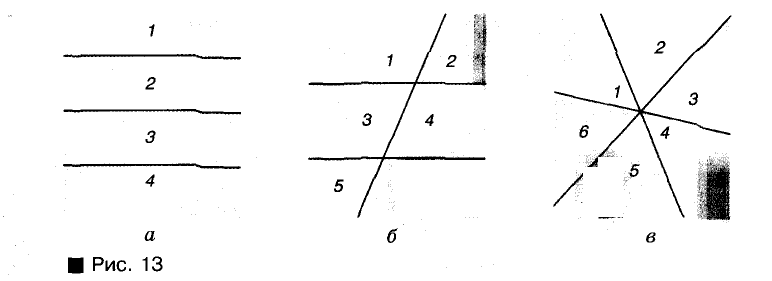
Если прямые расположены, как показано на рисунке 12, то они разбивают плоскость на 7 частей. Если они расположены, как показано на рисунке 13, то они разбивают плоскость на «4 или 6 частей.

Ответ. Три прямые разбивают плоскость, которой они принадлежат, на 4, 6 или 7 частей.
 

Дополнительное объяснение точки и прямой:

Основными геометрическими фигурами на плоскости являются точка и прямая. Плоскость можно представить как лист бумаги, точку — как след, оставленный иголкой на этом листе, а прямую — как тонкую натянутую нить. Точки обычно обозначают прописными латинскими буквами (А, В, С, D, ...), а прямые — строчными латинскими буквами (а, b, с, d, ...).

Ha рисунке 1 точки А и D лежат на прямой , а точки В и С не лежат на прямой . Можно это же сказать иначе: прямая 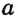проходит через точки

А и D, но не проходит через точки В и С.

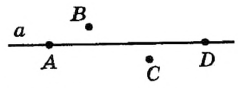
Рис. 1

Прямая бесконечна и состоит из бесконечного множества точек. На рисунках мы изображаем лишь часть прямой.

Свойства точек и прямых

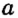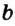Через одну точку на плоскости можно провести бесконечно много прямых. Рассмотрим прямые и , проходящие через точку С (рис. 2). В этом случае говорят, что прямые

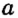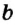и пересекаются в точке С, а их общая точка С является точкой пересечения прямых 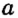и .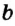

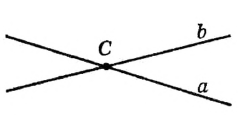
Рис. 2

Если на плоскости обозначены две точки ^[1] А и В, то через них можно провести прямую с (рис. 3). Отметим, что через точки А и B невозможно провести другую прямую, которая не совпадала бы с прямой с.

Это свойство называют аксиомой проведения прямой.

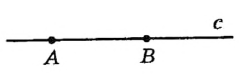
Рис. 3

^[1] Здесь и далее, говоря «две точки» («две прямые», «три точки» и т. д.), мы будем считать, что эти точки (прямые) различны.

Аксиома проведения прямой

Через любые две точки можно провести прямую, и притом только одну.

Аксиома - от греческого «аксиос» - общепринятый, безоговорочный, не вызывающий сомнения

Из этого следует, что две прямые не могут иметь две или более общих точек: они либо имеют одну общую точку, либо не имеют общих точек вообще. Прямую, с выбранными на ней двумя точками, можно обозначать прописными буквами, которыми названы эти точки. Так, прямую на рисунке 3 можно назвать прямой АВ или прямой ВА.

Через три точки плоскости не всегда можно провести прямую. Так на рисунке 1 нельзя провести прямую через точки А, В, D.

На рисунке 4 точки А, В, С лежат на одной прямой, причем точка С лежит между точками А и В. Можно также сказать, что точки А и В лежат по разные стороны от точки С.

Точки В и С лежат по одну сторону от точки А , а точки А и С лежат по одну сторону от точки В.

Аксиома расположения точек на прямой:

Из трех точек на прямой одна и только одна лежит между двумя другими.

Луч

Любая точка делит прямую на две части (рис. 5). Каждую из этих частей можно условно считать половиной прямой, поэтому образовавшиеся части прямой и получили название «полупрямые», или иначе — лучи

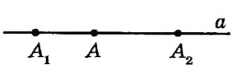
Рис. 5 Точка А делит прямую а на две полупрямые 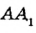и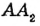

Лучом (или полупрямой) называется часть прямой, состоящая из всех Точек этой прямой, лежащих по одну сторону от некоторой данной на ней точки, а также самой этой точки. Данная точка называется начальной точкой (или началом) луча.

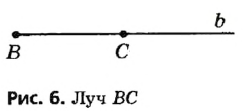
На рисунке 5 точка А — начальная точка двух лучей прямой 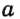. Лучи, как и прямые, можно обозначать строчными латинскими буквами или двумя точками: начальной (обязательно на первом месте!) и еще какои-нибудь точкой этого луча. Так, луч на рисунке 6 можно обозначить 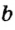или ВС , но нельзя обозначить СВ.

Два различных луча одной прямой с общей начальной точкой называются дополнительными лучами.

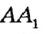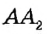На рисунке 5 и — дополнительные лучи. Они дополняют друг друга до прямой 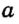и имеют только одну общую точку — их начало.

Пример №2

На прямой точка С лежит между точками А и В. Могут ли лучи АВ и АС быть дополнительными? Ответ обоснуйте.

Решение:

Пусть А, В и С — данные точки (рис. 7). Поскольку точка С лежит между точками А и В, то точки С и В лежат по одну сторону от точки А, значит, они принадлежат одному лучу с началом А. Этот луч можно назвать АВ или АС. Следовательно, данные лучи совпадают, поэтому они не являются дополнительными.

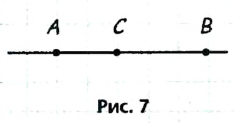
Ответ: не могут.

Отрезки и их длины

Две точки прямой делят эту прямую на три части: два луча и отрезок.

Отрезком АВ называется та часть прямой, которая состоит из точек А а В и всех точек, лежащих между ними. Точки А и В называют концами отрезка АВ. Все другие точки этого отрезка — его внутренние точки.

На рисунке 19 изображен отрезок АВ.

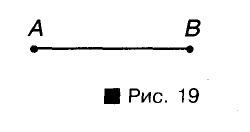
Точки А и В — его концы, а любая точка, лежащая между А и В, — внутренняя точка отрезка АВ.

Два отрезка пересекаются, если они имеют только одну общую внутреннюю точку.

Чтобы измерять отрезки, нужно иметь единичный отрезок (единицу измерения).

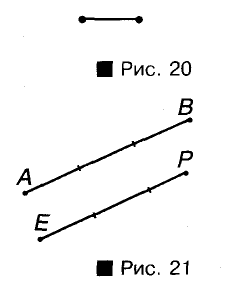
Отрезок, показанный на рисунке 20, будем считать единичным. Его длина равна 1 см.

Если на отрезке АВ единичный отрезок откладывается ровно 3 раза, то это значит, что длина отрезка АВ равна 3 см (рис. 21). Если на отрезке ЕР единичный отрезок откладывается два раза с остатком, а в остатке десятая часть единичного отрезка — 7 раз, то длина отрезка ЕР равна 2,7 см. Записывают так: АВ = 3 см, ЕР = 2,7 см.

За единичный отрезок можно брать отрезки длиной 1 м, 1 км, I фут, 1 дюйм и т. д.

Каждый отрезок имеет определенную длину.

Два отрезка называются равными, если длины их равны. Из двух отрезков большим считается тот, длина которого больше.

В сантиметрах измеряют сравнительно небольшие отрезки. Большие отрезки измеряют в дециметрах, метрах, километрах; меньшие — в миллиметрах. Напомним, что

1 км = 1000 м, 1 м = 10 дм = 100 см = 1000 мм.

Длину отрезка называют также расстоянием между его концами. Если ХУ = 18 см, то это означает, что расстояние между точками X и У равно 18 см. Расстояние между X и У всегда равно расстоянию между У и X.

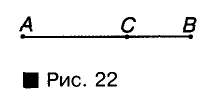
Если точка С отрезка АВ разбивает его на две части, длины которых равны, например 2 см и 1,2 см, то длина отрезка АВ равна 3,2 см (рис. 22).
 

Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Напечатанные выше жирным шрифтом два предложения со значком  — это основные свойства измерения отрезков.

Серединой отрезка называется его внутренняя точка, разбивающая этот отрезок на две равные части.

Если точка С — середина отрезка АВ, то АС = СВ (рис. 23).

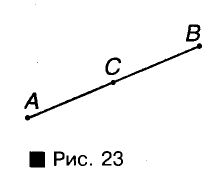
Если точка С не принадлежит отрезку АВ, то сумма длин отрезков АС и СВ больше длины АВ. Таким образом, для любых трех точек А, В и С всегда АВ + ВС > АС.

Измерять длины отрезков приходится многим специалистам. Чертежники измеряют их масштабными линейками, столяры — складными метрами, портные — клеенчатыми сантиметрами, строители — рулетками (рис. 24).

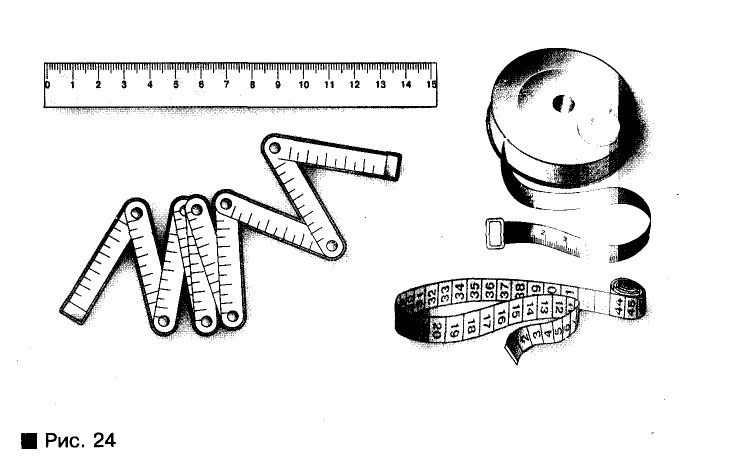
Для любознательных:

Измерительные приборы обеспечивают ту или иную точность. Расстояние между городами обычно определяют с точностью до километра, между берегами реки — с точностью до метра, длину карандаша — с точностью до миллиметра, диаметр детали ручных часов — с точностью до десятой, а то и сотой части миллиметра. Разумеется, для измерений разных длин и расстояний используют соответствующие измерительные приборы: кроме уже названных, циркули, кронциркули, штангенциркули, дальномеры и др. С некоторыми из них вы познакомитесь позже. Единицы длины бывают разные. В англоязычных странах чаще всего используют следующие: фут, дюйм, миля. Подробнее о них — дальше.

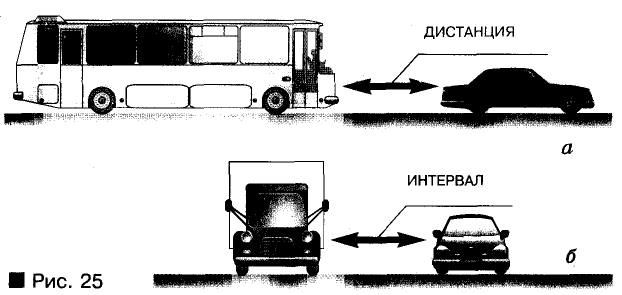
На практике для различных расстояний существуют разные названия: длина, ширина, высота, глубина, дистанция, интервал (рис. 25).
 

Пример №3

 Луч — часть прямой. Можно ли утверждать, что луч короче прямой?

Решение:

Прямая и луч не имеют длины, поэтому сравнивать и длины нет смысла.

Ответ. Нет.

Пример №4

Точки К, Р и Т лежат на одной прямой. Найдите расстояние между Р и Т, если КР ~ 1,7 м, КТ = 4,8 м. Сколько решений имеет задача?

Решение:

Отметим точки К и Т так, что КТ = 4,8 м. Точка Р пр* мой КТ находится на расстоянии 1,7 м от К. Возможно два случая (рис. 26):

а) К лежит между PvlT: РТ = 1,7 м + 4,8 м = 6,5 м;

б) Р лежит между К и Т: РТ = 4,8 м - 1,7 м = 3,1 м.
 

Ответ. Задача имеет два решения: 6,5 м; 3,1 м.

Углы и их меры

Два луча, имеющих общее начало, разделяют плоскость на две части.

Часть плоскости, ограниченная двумя лучами с общим началом, называется углом.

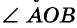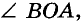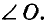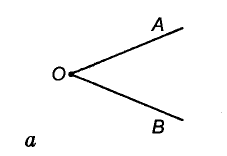
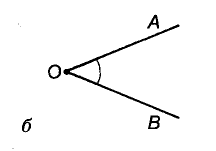
Лучи, ограничивающие угол, называются сторонами, а их общее начало - вершиной уела (рис. 30, а). Такой угол называют углом А О В, или углом В О А, или углом О и записывают соответственно: , или или Все точки угла, не принадлежащие его сторонам, образуют внутреннюю область этого угла. Внутренняя область угла на рисунке 30, а закрашена. Иногда внутреннюю область угла обозначают дугой, иногда никак не обозначают, а только представляют себе. На рисунке 30, б, в вы видите углы с вершиной О и сторонами ОА и ОВ.

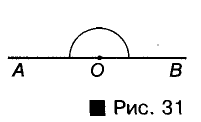
Угол, стороны которого — дополнительные лучи, называют развернутым углом (рис. 31).

Чтобы измерять углы, необходимо иметь единицу измерения. Такой единицей принято считать угол в 1 градус (сокращенно: 1°).

В развернутом угле он вмещается 180 раз.

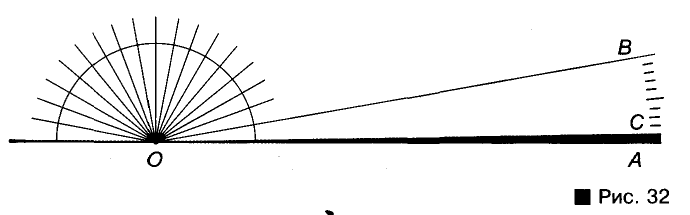
Представим полуокружность, разделенную на 18 равных дуг (рис. 32). Если из ее центра О через все точки деления и концы полуокружности провести лучи, они разделят развернутый угол на 18 углов по 10°. Один из таких углов (АОВ) делим на 10°. Мера угла АОС равна 1°.

Каждый угол имеет определенную меру.

Мера развернутого угла равна 180°.

Меру угла обозначают так же, как и угол. Например, если мера угла ABC равна 60 градусам, пишут: 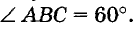Очень маленькие углы измеряют в минутах и секундах.

Минутой называют 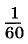 часть градуса, а секундой —  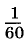часть минуты.

Записывают так: 1° = 60', 1' = 60".

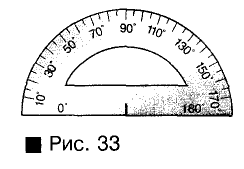
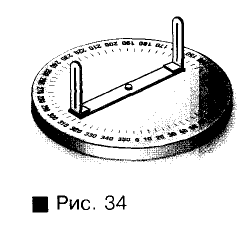
Углы в тетради и на классной доске измеряют транспортиром (рис. 33), а на местности — астролябией (рис. 34), теодолитом (рис. 35) или другими угломерными приборами.

Два угла называются равными, если их меры равны.

Из двух углов большим считается тот, мера которого больше.

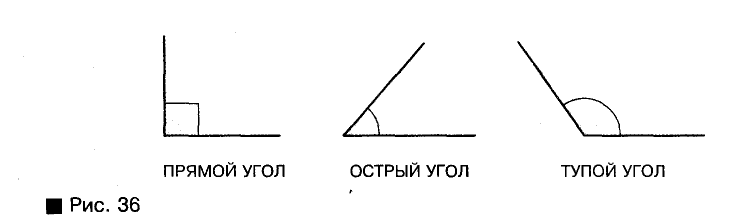
Угол называется прямым, если его мера равна 90°, острым — если он меньше прямого, тупым — если он больше прямого, но меньше развернутого (рис. 36).

Прямые углы на рисунках чаще обозначают не дугами, а квадратиками.

Углы больше развернутого (см. рис. 30, в) пока рассматривать не будем.

Луч, который исходит из вершины угла и лежит в его внутренней области,
называют внутренним лучом угла.

Внутренний луч делит данный угол на дна меньших угла. Например, внутренний луч ОК угла АОВ делит этот угол на углы АОК и КОВ (рис. 37). При этом 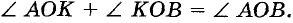Говорят, что угол АОВ равен сумме углов АОК и КОВ.

Мера угла равна сумме мер углов, на которые данный угол делится его внутренним лучом.

Два выделенных выше предложения со значком в — это основные свойства измерения углов.

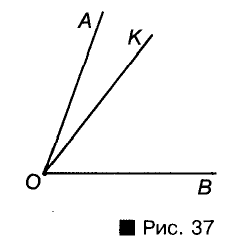
Внутренний луч, который делит угол на два равных угла, называется биссектрисой этого угла. На рисунке 38 луч

ОС — биссектриса угла АОВ.

Для любознательных:

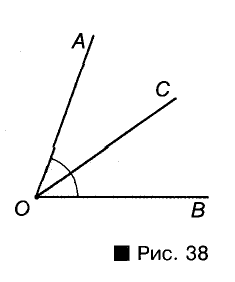
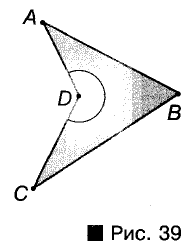
Углом часто называют также фигуру, составленную из двух лучей, имеющих общее начало, то есть углом называют и некую линию. Но разделить подобный угол на два или более равных углов нельзя. Таким образом, когда говорят о сложении, вычитании или делении углов, то угол рассматривают вместе с его внутренней областью. И хотя далее мы будем рассматривать в основном углы меньше развернутого, необходимо помнить, что бывают углы и больше развернутого, то есть больше 180°. Таким, например, является угол  D четырехугольника ABCD (рис. 39).

Существуют и специальные транспортиры,  которыми измеряют углы больше развернутого (рис. 40). Понятие угла часто используют также для характеристики поворотов. Например, велосипедное колесо можно повернуть на 100°, можно на 300°. А если колесо сделало полтора оборота? Считают, что оно повернулось на 360° и еще на 180°, всего — на 540°.

Кроме градусов, минут и секунд, существуют и другие меры углов. Моряки измеряют углы в румбах. Румбом называют одну восьмую часть прямого угла, 1 румб = 11,25° (рис. 41). Научные работники чаще всего измеряют углы в радианах. Что это такое, вы узнаете в старших классах.

Пример №5

Найдите меру угла А О В, если лучи ОС и О К делят его на три равных угла и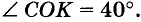  

Решение:

Угол СОК — третья часть угла АО В. Поэтому 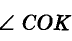= 40° 3 = 120°.

Ответ. 120°.

Пример №6

Найдите меры углов, образованных стрелками часов: в 3 часа; в 5 часов (рис. 42).

Решение:

На циферблате часов полуокружность соответствует 6 часам. Поэтому одному часу соответствует 1/6 часть развернутого угла, то есть 30°. Когда часы показывают 3 часа, угол между часовой и минутной стрелками равен 30° • 3 =

= 90°. Когда часы показывают 5 часов, угол между стрелками равен 30° 5 = 150°.

Ответ. 90°; 150°.

Определение и его роль в геометрии

В пункте 1.3 описаны два понятия — «луч», которое известно вам из курса математики 5 класса, и новое понятие — «дополнительные лучи». Благодаря этим описаниям можно четко представить, какие именно фигуры рассматриваются. Данные нами описания являются определениями, указывающими на особенности описанной фигуры, которые отличают ее от других фигур.

Прочитаем еще раз определение дополнительных лучей. Если в нем пропустить лишь слова «одной прямой», то лучи MN и МК на рисунке 8, а придется считать дополнительными. Если же не уточнить, что дополнительные лучи должны иметь общее начало, то лучи АВ и CD на рисунке 8, б тоже следует назвать дополнительными. Таким образом, эти измененные определения не будут описывать тот объект, который мы имеем в виду.

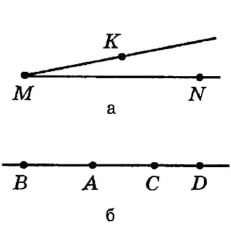
Рис. 8. К объяснению понятия «дополнительные лучи»:

а) лучи MN и МК не дополнительные;

б) лучи АВ и CD не дополнительные

Эти соображения свидетельствуют о том, как важно уделять внимание каждому слову в определении: только так можно по-настоящему понять геометрию.

Отрезок. Измерение и откладывание отрезков

Определение отрезка

Любой луч является частью прямой, «ограниченной» с одной стороны начальной точкой. Рассмотрим теперь отрезок — часть прямой, «ограниченную» точками с обеих сторон. Определение Отрезком называется часть прямой, состоящая из двух данных точек этой прямой (концов отрезка) и всех точек, лежащих между ними. Отрезок обозначают, записывая его концы в произвольном порядке. Так, отрезок на рисунке 10 можно назвать «отрезок АВ » или «отрезок ВА». Очевидно, что отрезок АВ является частью прямой АВ. При этом следует различать, идет ли речь о прямой АВ или об отрезке АВ.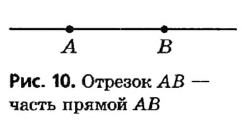

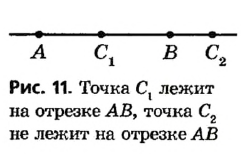
Если рассмотреть вместе с точками А и В некоторую другую точку прямой, то, в соответствии с аксиомой расположения точек на прямой, она либо лежит между точками А и В , то есть принадлежит отрезку АВ (на рисунке 11 такой точкой является 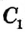), либо не лежит между точками А и В , то есть не принадлежит отрезку АВ (на рисунке 11 такой точкой является ).

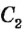Равенство отрезков. Середина отрезка

Определение:

Два отрезка называются: равными, если они совмещаются наложением.

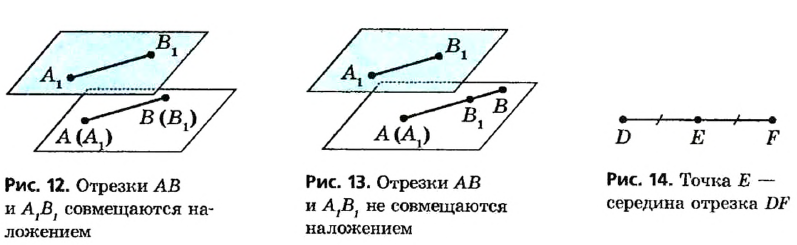
Нанесем отрезок 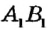на прозрачную пленку и наложим erqm отрезок АВ так, чтобы точка А, совпала с точкой А и эти отрезки имели другие общие точки. Если точка В, совместится с точкой В (рис. 12), то отрезки АВ и 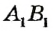равны (пишут так: 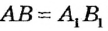). Если же точки В и 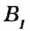не совместятся, то меньшим из двух отрезков является тот, который составляет часть другого. На рисунке 13 точка В, совместилась с некоторой точкой отрезка АВ, отличной от точки В, поэтому отрезок 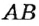больше отрезка 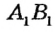. Кратко это обозначают так: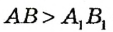

Определение:

Серединой отрезка называется точка отрезка, делящая его пополам (то есть на два равных отрезка).

На рисунке 14 отрезки DE и EF равны, то есть точка Е — середина отрезка DF. Обычно на рисунках равные отрезки обозначают одинаковым количеством черточек.

Измерение и откладывание отрезков

Важным свойством отрезка является его длина. Она выражается положительным числом, которое может быть определено сравнением данного отрезка с отрезком, принятым за единицу измерения,— единичным отрезком. В качестве единичного отрезка можно выбрать отрезок любой длины. На практике выбирают единичные отрезки длиной 1 мм, 1 см, 1 м и др.

Например, на измерительной линейке, которой мы обычно пользуемся, маленькие деления задают единичные отрезки длиной 1 миллиметр, а большие — длиной 1 сантиметр (рис. 15).

Прикладывая линейку к данному отрезку, мы определяем, сколько единичных отрезков и их частей в нем содержится. Это число выражает длину отрезка. Число, выражающее длину отрезка, зависит от единицы измерения.

На рисунке 15 длина отрезка СЕ равна 70 мм, или 7 см, или 0,07 м и т. д. Длина отрезка CD равна 3 см, а отрезка DE — 4 см. Можно сказать, что отрезок СЕ состоит из двух частей — отрезков CD и DE . Точка D лежит между точками С и Е, а длина отрезка СЕ равна сумме длин отрезков CD и DE (пишут так: CD + DE = СЕ ).

Сформулируем аксиомы измерения и откладывания отрезков.

Аксиома измерения отрезков

Каждый отрезок имеет определенную длину, которая выражается положительным числом в заданных единицах измерения. Длина отрезка равна сумме длин частей, на которые отрезок делится любой его точкой.

Аксиома откладывания отрезков

Hа любом луче от его начальной точки можно отложить отрезок данной длины и только один.

Очевидно, что измерение отрезков состоит в последовательном наложении на данный отрезок определенного количества единичных отрезков. Поэтому равные отрезки имеют равные длины, а больший отрезок имеет большую длину. Верно и другое утверждение: если отрезки имеют равные длины, то они равны, а большим из двух отрезков является тот, который имеет большую длину. Таким образом, для сравнения отрезков можно сравнить их длины.

Длину отрезка АВ называют также расстоянием между точка ми А и В. Часто, говоря «отрезок AB », мы имеем в виду его длину.

Пример №7

На луче АВ отмечена точка С, причем АВ = 12см, ВС - 7 см. Найдите длину отрезка АС

Решение:

Рассмотрим два случая расположения точки С на луче АВ.

1. Точка С не лежит на: отрезке АВ (рис. 16, а). Тогда точка В лежит на отрезке АС По аксиоме измерения отрезков АС = АВ + ВС, то есть АС = 12 +7 =19 (см).
2. Точка С лежит на отрезке АВ (рис. 16, 6). Тогда АВ = АС + ВС, то есть 12= АС + 7. Таким образом, АС = 12 - 7 = 5 (см).

Ответ: 19 см или 5 см.

Измерение, откладывание и определение углов

При изучении дополнительных лучей мы рассматривали случай, когда два луча имеют общую начальную точку. Рассмотрим теперь случай, когда два луча имеют общую начальную точку, но не обязательно являются полупрямыми одной прямой.

Определение:

Углом называется геометрическая фигура, которая состоит из двух лучей (сторон угла), исходящих из одной точки (вершины угла).

Для обозначения углов используют знак 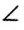. На рисунке 17, а изображен угол с вершиной В, сторонами которого являются луч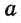и и 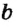(или ВА и ВС ). Этот угол можно обозначить одним из следующих способов: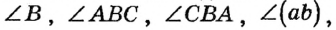 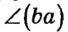. Если угол обозначают по вершине и двум точкам на сторонах, то вершину обязательно указывают на втором месте. Иногда углы обозначают греческими буквами 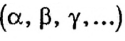(рис. 17, б), или числами (рис. 17, в).

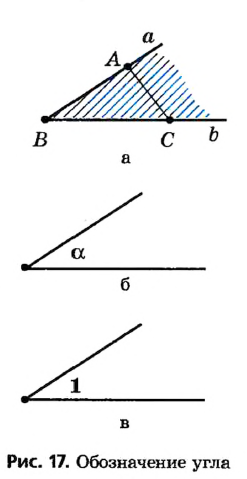
Стороны угла делят плоскость на две части. Внутренней областью угла считается та из них, которая целиком содержит любой отрезок с концами на сторонах угла (на рисунке 17, а она заштрихована). Луч, который исходит из вершины угла и проходит в его внутренней области, делит данный угол на два угла. На рисунке 18 луч BD делит угол ABC на углы ABD и DBC .

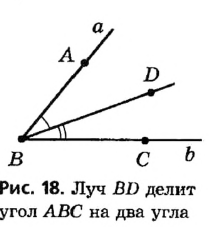
Определение:

Развернутым углом называется угол, стороны которого являются дополнительными лучами.

На рисунке 19 изображен развернутый угол АОВ.

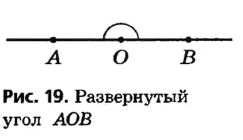
Прямая АВ делит плоскость на две части, каждую из которых можно считать внутренней областью развернутого угла АОВ . Договоримся ту из частей, которую мы рассматриваем как внутреннюю, обозначать дужкой.

Равенство углов. Биссектриса угла

Определение:

Два угла называются равными, если они совмещаются наложением.

Биссектриса - от латинского «бис» — дважды и «секто» — рассекающая пополам.

На рисунке 20 изображены углы 1 и 2. Наложим угол 1 на угол 2 так, чтобы их вершины совпали, сторона первого угла совместилась со стороной второго, а внутренние области этих углов были расположены по одну сторону от прямой, содержащей совместившиеся стороны. Если другие стороны этих углов тоже совместятся, то углы 1 и 2 являются равными (пишут так: ).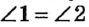

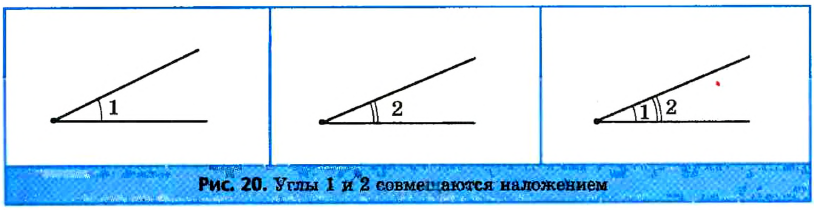
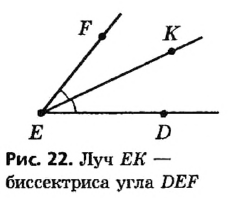
Если же эти стороны не совместятся, то меньшим считается тот угол, сторона которого принадлежит внутренней области второго угла. На рисунке 21 угол 1 является частью угла 2, то есть он меньше угла 2 (пишут так: ).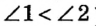

Определение

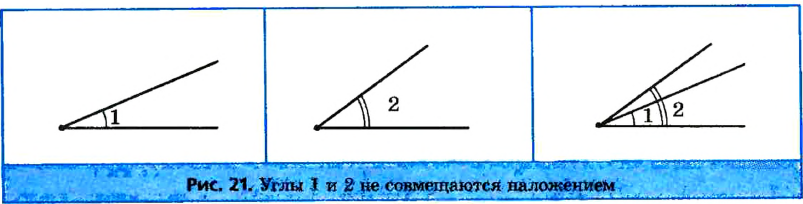
Биссектрисой угла называется луч, который исходит из вершины угла и делит угол пополам (то есть на два равных угла).

На рисунке 22 углы DEK и KEF равны, поэтому луч ЕК — биссектриса угла DEF . Обычно на рисунках равные углы обозначают одинаковым количеством дужек.

Измерение и откладывание углов

Измерение углов имеет много общего с измерением отрезков. Величина отрезка количественно выражается мерой (длиной) отрезка, а величина угла — мерой угла. Мера угла выражается положительным числом, которое можно определить измерением, основанным на сравнении данного угла с углом, принятым за единицу измерения.

Обычно такой единицей является 1 гра дус (обозначается 1°) — угол, равный 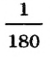части развёрнутого угла. Градусная мера угла указывает, сколько углов величиной 1° и их частей содержится в данном угле. Для измерения углов обычно используют транспортир, деления которого задают меру угла в градусах (Рис. 23)

Градус - от латинского «градус» - шаг. По наблюдению вавилонян солнечный диск на дневном пути «делает 180 шагов».

Сформулируем аксиомы измерения и откладывания углов.

Аксиома измерения углов

Каждый угол имеет градусную меру. Которая выражается положительным числом. Развернутый угол равен 180°.

Если луч делит Данный угол на два угла, то градусная мера данного угла равна сумме градусных мер двух полученных углов;

Аксиома откладывания углов

От любого луча данной прямой можно отложить в заданную сторону от прямой угол с заданной градусной мерой, меньшей 180°, и только один.

Так, на рисунке 18 градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (это утверждение можно записать в виде равенства: 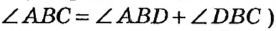Часто, говоря «угол ABC >, мы имеем в виду градусную меру этого угла.

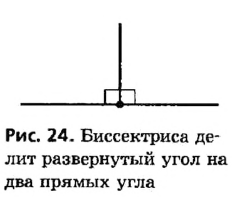
Биссектриса развернутого угла делит его на два угла, каждый из которых равен 90° (рис. 24). Такие углы называются прямыми. В отличие от других углов, обычно обозначаемых дужками, прямой угол обозначают знаком .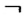

В 7 классе мы будем рассматривать углы, градусная мера которых не превышает 180°. Для более точных измерений используется 1 минута (обозначается 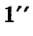) - 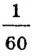часть минуты.

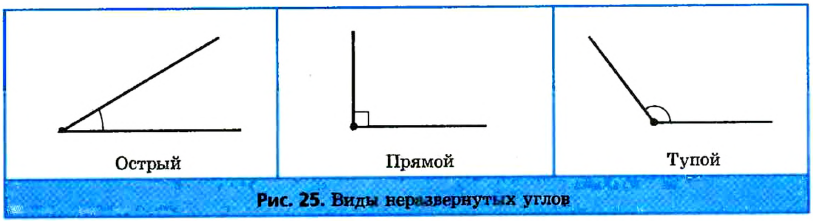
Неразвернутые углы делятся на три вида (рис. 25):

• острые углы, меньше 90°;
• прямые углы, равны 90°;
• тупые углы, больше 90°, но меньше 180°.

На практике для построения углов используют транспортир. Для построения прямых углов используют угольник.

Измерение углов можно считать последовательным наложением на данный угол определенного (не обязательно целого) числа углов, равных 1°. Поэтому равные углы имеют равные градусные меры, а больший угол имеет большую градусную меру. Верно и другое утверждение: если углы имеют равные градусные меры, то они равны, а из двух углов большим является тот, который имеет большую градусную меру. Таким образом, для сравнения двух углов достаточно сравнить их градусные меры.

Пример №8

Луч b делит угол (aс), равный 120° на два угла, один, из которых втрое меньше угла (ас) .

Найдите эти углы.

Решение:

Пусть угол ( ab) втрое меньше угла (ас). Тогда 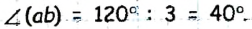Согласно аксиоме измерения углов, если луч b делит угол (ас) на два угла, то их сумма равна данному углу: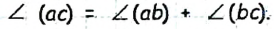

Тогда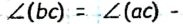

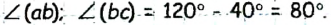
Ответ: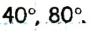

Аналогия в геометрии

Иногда при решении задач о свойствах отрезков и углов применяются одни и те же методы и подходы. Это объясняется сходством некоторых свойств этих фигур. Такое сходство в науке называется аналогией.

Объясним суть аналогии на примере двух следующих задач.

Задача 1

На отрезке АВ, равном 20 см, отмечена точка С. Найдите расстояние между серединами отрезков АС и СВ.

Задача 2

Луч С делит угол (аb), равный 140°, на два угла. Найдите угол между биссектрисами углов (ас) и (ab).

На первый взгляд, перед нами совершенно разные задачи, поскольку в одной речь идет об отрезках, а во второй — об углах. Однако в обеих задачах дано некоторое «целое», разделенное на части. Кроме того, понятия середины отрезка и биссектрисы угла связаны с делением целого пополам, и в обеих задачах нам необходимо найти сумму половин каждой из частей фигуры.

Решение 1

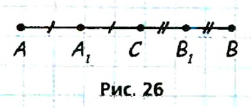
Пусть точка С принадлежит отрезку АВ, точк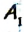и и 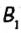— середины отрезков АС и СВ соответственно (рис. 26). Тогда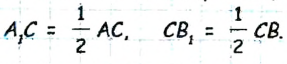

Найдем длину отрезка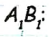

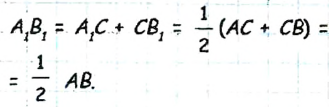
Поскольку по условию задачи АВ = 20 см, имеем: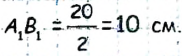

Ответ: 10 см

Решение 2

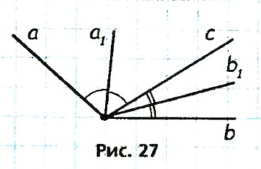
Пусть луч с делит угол (аb) на два угла, луч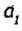и и 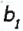— биссектрисы углов (ас) и (cb) соответственно (рис. 27).

Тогда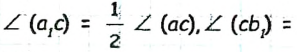

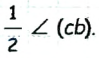
Найдем градусную меру угла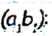

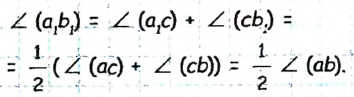
Поскольку по условию задачи 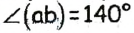имеем: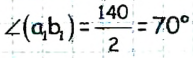

Ответ: 70°.

Как видим, в основе обоих решений лежит общая идея. Найдя ее при решении первой задачи, мы можем повторить основные этапы рассуждений применительно к условиям второй задачи, то есть решить ее аналогично.

Рассуждения по аналогии довольно часто применяются и в других науках. Например, биологи установили, что летучая мышь в полете испускает ультразвуковые колебания и, воспринимая колебания, отраженные от преграды, ориентируется по этим сигналам в темноте. По аналогичному принципу ученые создали радиолокатор, определяющий местонахождение объектов в любых погодных условиях. Но аналогия в науке не всегда дает желаемый результат: в течение многих веков человек старался взлететь в небо с помощью искусственных крыльев, аналогичных птичьим, но эти старания были напрасными. И только более основательные научные исследования привели к созданию дельтапланов, самолетов и других летательных аппаратов, с помощью которых человек поднялся в воздух. Выдающийся немецкий астроном и математик Иоганн Кеплер считал аналогии «своими верными учителями» и подчеркивал, что «аналогиями менее всего следует пренебрегать в геометрии». Однако при этом нужно учитывать, что аналогия, полезная как способ рассуждений, сама по себе не может служить доказательством каких-либо свойств геометрических фигур.

Определение параллельных прямых

Известно, что если две прямые на плоскости имеют только одну общую точку, то они пересекаются. Рассмотрим теперь случай, когда две прямые не имеют общих точек.

Параллельный - от греческого слова «параляелос» — идущий рядом

Определение:

Две прямые на плоскости называются параллельными, если они не пересекаются.

Представление о параллельных прямых дают, например, железнодорожные рельсы или линейки нотного стана.

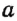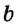На рисунке 29 прямые и параллельны. Кратко это обозначают так: 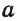|| 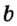. Такая запись читается: «Прямая 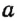параллельна прямой »

Итак, можно выделить два случая взаимного расположения прямых на плоскости: две прямые на плоскости или параллельны, или пересекаются.

Наряду с параллельностью прямых мы будем рассматривать также параллельность отрезков и лучей.

Определение:

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Аналогично формулируются определения параллельности двух лучей, прямой и отрезка, луча и отрезка и т. п.

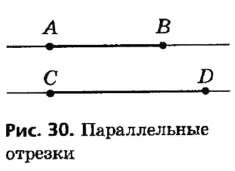
На рисунке 30 прямые АВ и CD параллельны, поэтому отрезки АВ и CD параллельны, лучи ВА и CD параллельны, отрезок АВ параллелен прямой CD и т. д.

На практике довольно часто приходится проводить прямую, параллельную данной,— например, делать разметку дороги или чертить поля в тетради. Всегда ли можно провести через данную точку прямую, параллельную данной? Сколько таких прямых проходит через точку, не лежащую на данной прямой? Ответ на эти вопросы дает аксиома параллельных прямых (аксиома Евклида).

Аксиома параллельных прямых (аксиома Евклида)

Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной¹.

Мы сформулировали лишь некоторые из аксиом планиметрии. Более полный перечень аксиом представлен в Приложении 1.

Теорема о двух прямых, параллельных третьей

На основе аксиом с помощью логических рассуждений (доказательств) мы будем получать новые геометрические факты. В математике утверждение, справедливость которого устанавливается путем доказательства, называется теоремой.

Доказывая теорему, используют определения, ак сиомы и теоремы, доказанные ранее.

Итак, сформулируем и докажем первую теоре му — теорему о параллельных прямых (рис. 31).

Теорема: (о двух прямых, параллельных третьей)

Две прямые, параллельные третьей, параллельны между собой.

' На самом деле имеет место такое утверждение: «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну». Возможность провести такую прямую мы докажем в п. 14.3.

Доказательство:

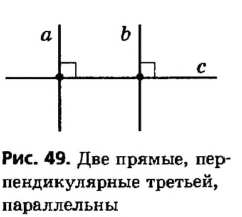
Пусть а, b и с — данные прямые, причем а || с, b || c. Докажем, что прямые а и b параллельны.

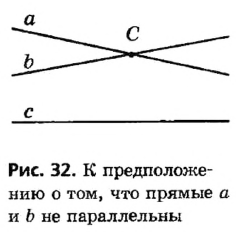
Предположим, что прямые а и b не параллельны. Тогда они должны пересекаться в некоторой точке С (рис. 32). Таким образом, через точку С проходят две прямые, параллельные прямой с. Но согласно аксиоме параллельных прямых через точку вне данной прямой может проходить не более одной прямой, параллельной данной. Следовательно, наше предположение о том, что прямые а и b могут пересекаться, неверно, то есть эти прямые параллельны. Теорема доказана.

Применим доказанную теорему для решения задачи.

Пример №9

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую. Докажите.

Решение:

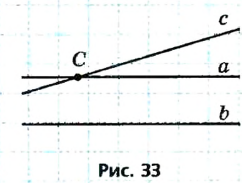
Пусть а || b, и прямая с пересекает прямую а (рис. 33). Докажем, что прямые b и с пересекаются. Предположим, что эти прямые не пересекаются. В таком случае b || с. Поскольку с || b и а || b, то по теореме о двух прямых, параллельных третьей, прямые а и с параллельны. Но это невозможно, так как по условию задачи прямые а и c пересекаются. Таким образом, предположение о том, что b || с, неверно. Значит, прямые b и с пересекаются, что и требовалось доказать.

Теорема - от греческого «теоремос» - рассматривать, обдумывать

Обратим внимание на рисунок 32, который использовался в ходе доказательства теоремы. Взаимное расположение прямых а, b, с на этом рисунке не соответствует формулировке теоремы, и это легко объяснить: ведь рисунок отражает предположение, впоследствии оказавшееся неверным. Вообще, рисункам в геометрических теоремах и задачах отводится особая роль — то, что на них изображено, следует из имеющихся у нас сведений, но не наоборот. Недоказанные свойства геометрических фигур, даже если они кажутся очевидными из рисунков, использовать нельзя. Рисунок в геометрии лишь отражает свойства и утверждения, выраженные словами, но сам по себе не является доказательством. К тому же рисунок может не охватывать всех возможных вариантов расположения элементов фигур, которые подразумеваются в задаче или теореме. Недаром геометрию называют «искусством правильно рассуждать на неправильных чертежах».

Условие и заключение теоремы. Доказательство от противного.

В формулировке любой теоремы всегда можно четко выделить две части: то, что дано (условие), и то, что надо доказать (заключение). Переформулируем теорему о двух прямых, параллельных третьей, следующим образом: «Если две прямые параллельны третьей прямой, то эти прямые параллельны между собой». Нам известно, что две прямые параллельны третьей прямой — это условие теоремы. Требуется доказать, что эти прямые параллельны между собой — это заключение теоремы. Вообще говоря, выделить условие и заключение легче всего для утверждения, представленного в виде: «Если... (условие), то... (заключение)».

Проанализируем доказательство теоремы о двух прямых, параллельных третьей. Сначала мы предположили, что прямые а и b не параллельны, то есть что заключение теоремы ошибочно. Затем, опираясь на известные свойства взаимного расположения прямых, установили, что через некоторую точку С проходят две прямые, параллельные с, то есть пришли к противоречию с аксиомой параллельных прямых. На основании этого противоречия мы сделали вывод о том, что наше предположение было неверным, а значит, верным является утверждение теоремы. Этот метод доказательства называется доказательством от противного, им мы воспользовались и в задаче, которую рассматривали после теоремы. Но этот метод не единственный: уже в следующем параграфе мы будем применять и другие методы доказательств.

Метод доказательства от противного иногда используется как в других науках, так и в повседневной жизни. Например, врач, чтобы убедиться, что пациент не болен гриппом, может рассуждать так: «Допустим, что у больного грипп; тогда у него должны быть характерные симптомы: повышение температуры, головная боль и т. п. Но этих симптомов нет, то есть предположение о гриппе неверно. Значит, пациент не болен гриппом».

Схема доказательства от противного

Утверждение:	Если А, то В
	Доказательство:
1. Пусть A, но не B	Предполагаем, что условие теоремы выполняется, а заключение — нет
2.Рассуждения	Проводим рассуждения, опираясь на аксиомы и ранее доказанные теоремы
3.Противоречие	Получаем новое утверждение, противоречащее либо данному условию, либо одной из аксиом, либо ранее доказанной теореме
4. Тогда B	Убеждаемся, что наше предположение ошибочно, т. е. данное утверждение является верным

Определение смежных углов

В предыдущих параграфах мы рассматривали виды углов в зависимости от их градусной меры. Перейдем к изучению углов, имеющих общие элементы.

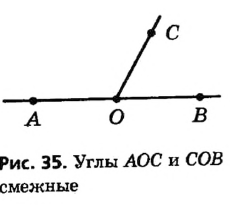
Пусть на прямой точка О лежит между точками А и В, а С — произвольная точка вне прямой АВ (рис. 35). Тогда углы АОС и СОВ имеют общую сторону, а стороны OA и ОВ данных углов являются дополнительными лучами.

Определение:

Два угла называются смежными, если они имеют общую сторону, а другие стороны этих углов являются дополнительными лучами.

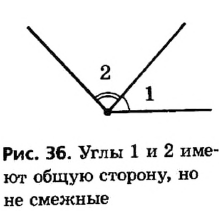
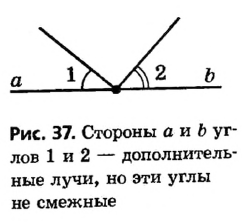
Пропуск хотя бы одного условия в формулировании определения недопустим; это может привести к тому, что будет описан иной геометрический объект. Так, если стороны двух углов не являются дополнительными лучами, то даже при наличии общей стороны такие углы — не смежные (рис. 36). Не являются смежными и углы, которые не удовлетворяют первому условию определения, то есть не имеют общей стороны (рис. 37).

Теорема о смежных углах. Следствия из теоремы

Теорема (о смежных углах)

Сумма смежных углов равна 180° .

Доказательство:

Пусть углы ( аb ) и (bс) — данные смежные углы (рис. 38). Тогда по определению смежных углов лучи а и с дополнительные, то есть угол (ас) развернутый, а его градусная мера равна 180°. Луч b делит угол (ас) на два угла, и по аксиоме измерения углов 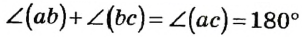. Теорема доказана.

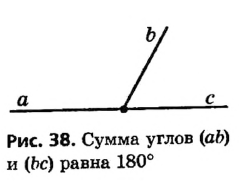
Сформулируем теперь несколько утверждений, которые легко обосновать с помощью доказанной теоремы.

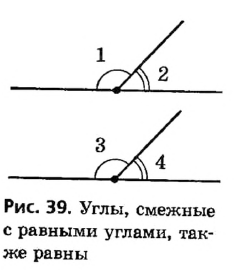
1. Если два угла равны, то смежные с ними углы также равны.

Действительно, по теореме о смежных углах 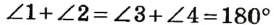(рис.39). Если 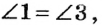то 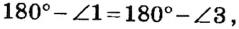то есть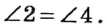

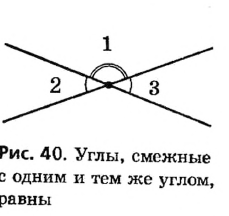
2. Два угла, смежные с одним и тем же углом, равны.

На рисунке 40 углы 1 и 2, а также углы 1 и 3 являются смежными. Поскольку сумма смежных углов равна 180°, то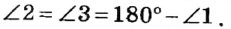

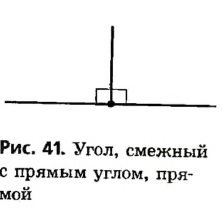
3. Угол, смежный с прямым углом, также прямой. Угол, смежный с тупым углом,— острый. Угол, смежный с острым углом,— тупой.

Эти утверждения вытекают из теоремы о смежных углах, поскольку 180°-90° = 90° (рис. 41), а если два неравных угла в сумме составляют 180°, то один из них больше 90° (то есть тупой), а второй — меньше 90° (то есть острый).

В математике утверждения, непосредственно вытекающие из теорем (или аксиом), называют следствиями. Обосновывая следствия 1—3, мы всякий раз упоминали теорему о смежных углах, причем делали это двумя способами: либо указывали ее название, либо пересказывали ее содержание. Такие обращения к известному утверждению с целью обоснования нового называют ссылками.

Решая геометрическую задачу или доказывая новую теорему, необходимо ссылаться на ранее изученные определения, аксиомы, теоремы и их следствия, а также на данные, содержащиеся в условии задачи или вытекающие из него. Например, при доказательстве теоремы о смежных углах мы ссылались на определения смежных углов, развернутого угла и аксиому измерения углов, а при доказательстве теоремы о двух прямых, параллельных третьей, — на аксиому параллельных прямых.

Пример №10

Докажите, что если два смежных угла равны, то они прямые.

Решение:

Если 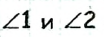— смежные углы, то 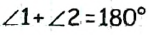(по теореме о смежных углах). Поскольку по условию задачи 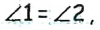то каждый из этих углов равен 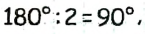то есть данные углы являются прямыми, что и требовалось доказать.

Вертикальные углы. Перпендикулярные прямые

Определение вертикальных углов

Рассмотрим еще один случай взаимного расположения углов с общими элементами. Вертикальный — от латинского «вертикалис» — вершинный

Определение:

Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон второго. На рисунке 44 прямые АС и BD пересекаются в точке О. Стороны OD и OA угла AOD являются дополнительными лучами сторон ОВ и ОС угла ВОС , поэтому эти углы — вертикальные. Вертикальными являются также углы АОВ и DОС.

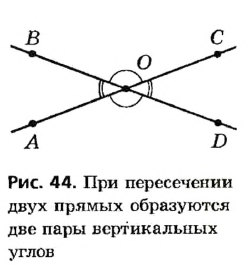
Таким образом, при пересечении двух прямых¹ образуются две пары вертикальных углов. Наглядное представление о вертикальных углах дают, например, обычные ножницы.

Теорема о вертикальных углах. Угол между прямыми

Основное свойство вертикальных углов выражает следующая теорема.

Теорема: (о вертикальных углах )

Вертикальные углы равны.

¹ Здесь и далее, говоря об углах, образованных при пересечении двух прямых, мы будем иметь в виду неразвернутые углы.

Доказательство:

Пусть 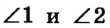— вертикальные углы, образовавшиеся при пересечении прямых а и b (рис. 45). Рассмотрим угол 3, сторонами которого также являются полупрямые прямых a и b . Углы 1 и 2 смежные с углом 3 (по определению смежных углов), поэтому по следствию из теоремы о смежных углах 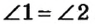. Теорема доказана.

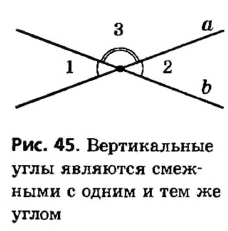
Пример №11

Сумма двух углов, образовавшихся при пересечении двух прямых, равна 100°. Найдите все образовавшиеся углы.

Решение:

По условию задачи при пересечении двух прямых образовались два угла, сумма которых составляет 100°. Эти углы могут быть или смежными, или вертикальными. Сумма смежных углов равна 180°, поэтому данные углы не могух быть смежными, значит, они вертикальные. Пусть 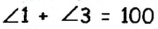(рис. 46). Так как вертикальные углы равны, то каждый из двух данных углов равен 100° : 2 = 50°. Таким образом, 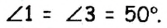Поскольку углы 1 и 2 смежные, то 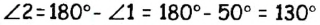(по теореме о смежных углах).

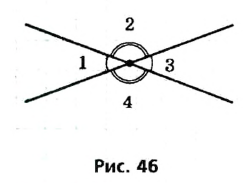
Поскольку углы 2 и 4 вертикальные, то 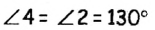(по теореме о вертикальных углах).

Ответ: 50°; 130°; 50°; 130°.

Определение:

Углом между двумя прямыми называется меньший из углов, образовавшихся при их пересечении.

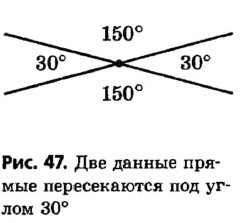
На рисунке 47 две прямые при пересечении образуют два угла по 30° и два угла по 150°. Угол между данными прямыми по определению равен 30° (иначе говорят: прямые пересекаются под углом 30°).

Очевидно, что если при пересечении двух прямых образуются четыре равных угла, то все они равны 90°, то есть данные прямые пересекаются под прямым углом.

Перпендикулярные прямые

Перпендикулярный— от латинского слова «перпендикулярис» - отвесный.

Определение:

Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

На рисунке 48 прямые а и b перпендикулярны. Кратко это обозначают так: .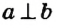

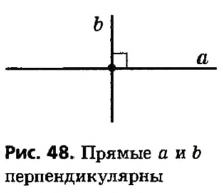
Отрезки или лучи называются перпендикулярными, если они лежат на перпендикулярных прямых.

Докажем важное утверждение; связывающее понятия перпендикулярности и параллельности прямых.

Теорема (о двух прямых, перпендикулярных третьей) Две прямые, перпендикулярные третьей, параллельны.

Утверждение теоремы иллюстрирует рисунок 49. На этом рисунке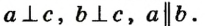

Доказательство:

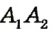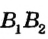Пусть даны прямые и , перпендикулярные прямой АВ. Докажем методом от противного, что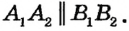

Предположим, что данные прямые не параллельны. Тогда они пересекаются в некоторой точке 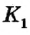(рис. 50).

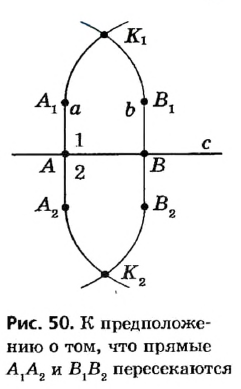
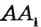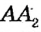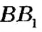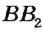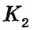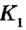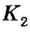Перегнем рисунок по прямой АВ. Поскольку прямые углы 1 и 2 равны, то при перегибе луч совместится с лучом . Аналогично луч совместится с лучом . Поэтому точка в которой пересекаются данные прямые, должна совместиться с некоторой точкой , также лежащей на этих прямых. Таким образом, через точки и проходят две прямые 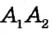и 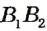, что невозможно по аксиоме проведения прямой. 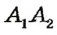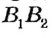Следовательно, наше предположение неверно, то есть прямые и параллельны. Теорема доказана.

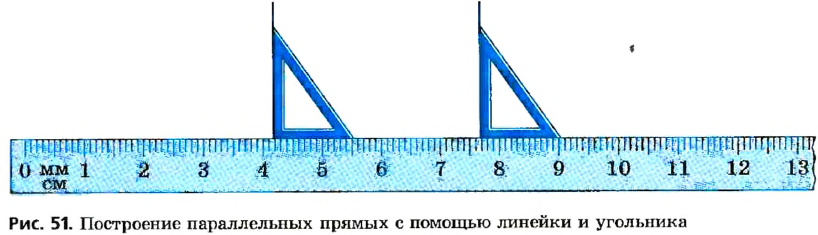
Свойство, описанное в теореме, используется для построения параллельных прямых с помощью линейки и угольника (рис. 51). Дважды прикладывая угольник к линейке, можно провести две прямые, перпендикулярные краю линейки. По доказанной теореме такие прямые параллельны.

Историческая справка

Древнейшая наука геометрия как и математика в целом, зарождалась из потребностей практической деятельности. Везде, где жили и работали люди, необходимо было измерять, вычислять, размышлять.

Первые документальные свидетельства о геометрических знаниях дошли до нас из Древнего Египта. Каждый год воды Нила затапливали почти все прибрежные земли, поэтому египтянам приходилось вновь их размежевывать. Именно так в процессе работы устанавливались простейшие свойства геометрических фигур.

Становление геометрии. Становление геометрии как строгой науки связано с работами древнегреческих ученых: Фалеса (ориент. 625-547 гг. до н.э.), Пифагора (ориент. 570-500 гг. до н. э.), Евдокса (ориент. 408-355 гг. до н. э.). Одной из выдающихся фигур в истории геометрии по праву считается Евклид Александрийский (ориент. 330-275 гг. до н. э.). Его произведение «Начала» стало учебником, по которому изучали геометрию на протяжении почти двух тысяч лет. Евклид первым применил именно тот подход к изложению геометрии, которым мы пользуемся сейчас: сначала сформулировал основные определения и свойства простейших фигур (аксиомы), а затем, опираясь на них, доказал многие другие утверждения.

Возведенные за две-четыре тысячи лет до нашей эры, египетские пирамиды и сегодня поражают точностью метрических отношений; строители уже тогда знали немало геометрических положений и расчетов.

Профессор Харьковского университета Алексей Васильевич Погорелое (1919-2002) обогатил современную геометрию новейшими исследованиями и создал школьный учебник, по которому занимались несколько поколений учащихся.

Исследования и открытия ученых- геометров нашли применение во многих областях человеческой деятельности. Геометрия стала элементом общечеловеческой культуры - ведь без знания основ геометрии невозможно представить себе современного просвещенного человека.

Герметрия в Украине Интересные страницы истории развития геометрии, в частности ее преподавания в школе, связаны с Украиной. Именно здесь, в одной из харьковских гимназий, в конце XIX в. начинал свою деятельность известный русский педагог Андрей Петрович Киселев (1852-1940). по учебнику которого изучали геометрию нэ протяжении почти 60 лет.

Справочный материал по простейшим геометрическим фигурам

1. Точки и прямые

• ✓ Основное свойство прямой. Через любые две точки можно провести прямую, и притом только одну.
• ✓ Две прямые, имеющие общую точку, называют пересекающимися.
• ✓ Любые две пересекающиеся прямые имеют только одну общую точку.

2. Отрезок и его длина

• ✓ Точки А и В прямой а (рис. 239) ограничивают часть прямой, которую вместе с точками А и В называют отрезком, а точки А и В — концами этого отрезка.
• ✓ Два отрезка называют равными, если их можно совместить наложением.
• ✓ Равные отрезки имеют равные длины, и наоборот, если длины отрезков равны, то равны и сами отрезки.
• ✓ Основное свойство длины отрезка. Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и СВ, то есть АВ = АС + СВ.
• ✓ Расстоянием между точками А и В называют длину отрезка АВ. Если точки А и В совпадают, то считают, что расстояние между ними равно нулю.

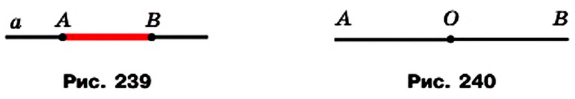
3. Луч. Угол

• ✓ Точка О прямой АВ (рис. 240) разбивает прямую на две части, каждую из которых вместе с точкой О называют лучом или полупрямой. Точку О называют началом луча.
• ✓ Два луча, имеющих общее начало и лежащих на одной прямой, называют дополнительными.
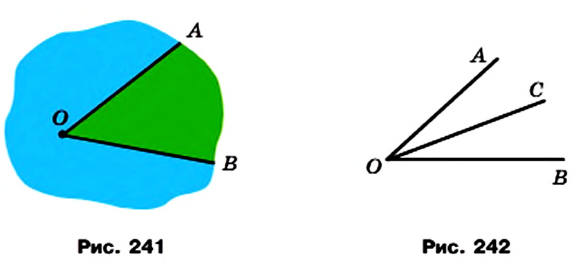
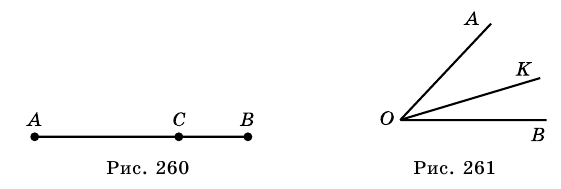
• ✓ Два луча ОА и ОВ, имеющие общее начало (рис. 241), разбивают плоскость на две части, каждую из которых вместе с лучами ОА и ОВ называют углом. Лучи ОА и ОВ называют сторонами угла, а точку О — вершиной угла.
• ✓ Угол, сторонами которого являются дополнительные лучи, называют развернутым.
• ✓ Два угла называют равными, если их можно совместить наложением.
• ✓ Биссектрисой угла называют луч с началом в вершине угла, делящий этот угол на два равных угла.

4. Измерение углов

• ✓ Каждый угол имеет определенную величину (градусную меру).
• ✓ Угол, градусная мера которого равна 90°, называют прямым. Угол, градусная мера которого меньше 90°, называют острым. Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
• ✓ Равные углы имеют равные величины, и наоборот, если величины углов равны, то равны и сами углы.
• ✓ Основное свойство величины угла. Если луч ОС делит угол АОВ на два угла АОС и СОВ (рис. 242), то

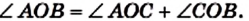
5. Смежные и вертикальные углы

• ✓ Два угла называют смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
• ✓ Сумма смежных углов равна 180°.
• ✓ Два угла называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого.
• ✓ Вертикальные углы равны.

6. Перпендикулярные прямые. Серединный перпендикуляр

• ✓ Две прямые называют перпендикулярными, если при их пересечении образовался прямой угол.
• ✓ Неперпендикулярные прямые при пересечении образуют пару равных острых углов и пару равных тупых углов. Величину острого угла называют углом между неперпендикулярными прямыми.
• ✓ Если прямые перпендикулярны, то считают, что угол между ними равен 90°.
• ✓ Два отрезка называют перпендикулярными, если они лежат на перпендикулярных прямых.
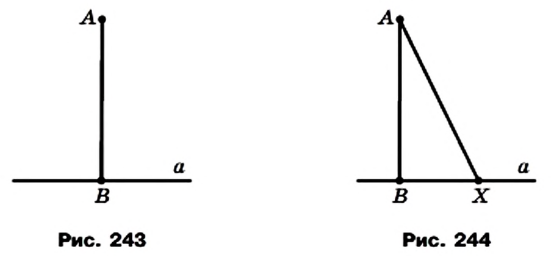
• ✓ На рисунке 243 изображены прямая а и перпендикулярный ей отрезок АВ, конец В которого принадлежит прямой а. В таком случае говорят, что из точки А на прямую а опущен перпендикуляр АВ. Точку В называют основанием перпендикуляра АВ.

• ✓ Длину перпендикуляра AB называют расстоянием от точки А до прямой а. Если точка А принадлежит прямой а, то считают, что расстояние от точки А до прямой а равно нулю.
• ✓Опустим из точки А на прямую а перпендикуляр АВ (рис. 244). Пусть X — произвольная точка прямой а, отличная от точки В. Отрезок АХ называют наклонной, проведенной из точки А к прямой а.
• ✓ Через данную точку проходит только одна прямая, перпендикулярная данной.
• ✓ Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.
• ✓ Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.
• ✓ Если точка равноудалена от концов отрезка, то она принадлежит серединному перпендикуляру этого отрезка.

Элементарные геометрические фигуры и их свойства

Основными геометрическими фигурами на плоскости являются точка и прямая.

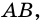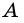Отрезком называют часть прямой, которая состоит из всех точек этой прямой, которые лежат между двумя ее точками, вместе с этими точками. На рисунке 257: отрезок  точки и 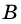- концы отрезка.

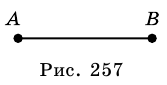
Точка 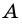делит прямую на две части (рис. 258). Каждую из полученных частей

вместе с точкой 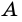называют лучом, выходящим из точки  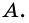Поэтому 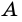называют началом каждого из лучей.

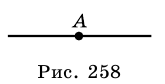
•  Два луча, имеющие общее начало и дополняющие друг друга до прямой, называют дополняющими.

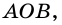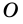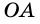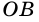Угол - это геометрическая фигура, состоящая из двух лучей, которые выходят из одной точки. Лучи называют сторонами угла, а их общее начало - вершиной угла. На рисунке 259: угол  точка - его вершина; и - стороны угла. Записать этот угол можно так: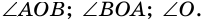

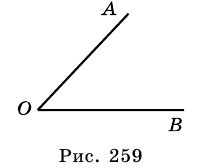
Биссектрисой угла называют луч, который выходит из вершины угла, проходит между его сторонами и делит его пополам.

Аксиомы планиметрии

• I.    Какова бы ни была прямая, существуют точки, принадлежащие ей, и точки, ей не принадлежащие.
• II.    Через две точки можно провести прямую и к тому же только одну.
• III.    Из трех точек на прямой одна и только одна лежит между двумя другими.
• IV.    Каждый отрезок имеет определенную длину, большую нуля.
• V.    Длина отрезка равна сумме длин частей, на которые он разбивается любой его внутренней точкой. (На рисунке 260
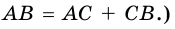
• VI.    Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°.
• VII. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. 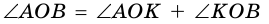(рис. 261).