Гармонические напряжения и токи

Содержание:

Гармонические напряжения и токи:

В предыдущих лекциях рассматривались электрические цепи при условии, что они находятся под воздействием постоянных напряжений и токов. В действительности же действующие в электрических цепях токи и напряжения являются переменными, т. е. представляют собой электрические колебания. Напомним, что колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени. Различают непериодические и периодические колебания.

Простейшим и в то же время наиболее важным типом периодических колебаний являются гармонические, когда колеблющаяся величина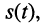

Исключительная роль гармонических колебаний в теории и практике радиотехники объясняется следующими обстоятельствами:

• они широко используются для передачи сигналов и электрической энергии (например, промышленный ток с частотой 50 Гц);
• применяются как простейший испытательный сигнал;
• являются единственным типом колебаний, форма которых не изменяется при прохождении через любую линейную систему;
• любое периодическое негармоническое колебание может быть представлено в виде суммы (наложения) различных                                    гармонических колебаний (такое представление называют спектром негармонического колебания).

Замечание:

Если временной интервал ограничен 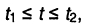 то имеет место отрезок гармонического колебания, который уже будет обладать отличными от гармонического колебания свойствами; при этом чем больше временной интервал, тем ближе свойства отрезка к свойствам самого гармонического колебания; во всём курсе лекций предполагается, что временной интервал исчисляется от нуля до бесконечности: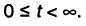

Определение гармонических напряжений и токов

Электрическое гармоническое колебание аналитически записывают в виде функции:

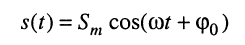
или

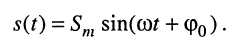
Традиционно в электротехнике используют синусную форму записи, а в теории электрических цепей (радиотехнике) — косинусную, которой, если это не оговаривается особо, и будем пользоваться в дальнейшем:

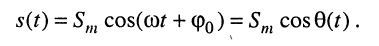      (7.1)

Если под колебанием 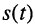понимать ток 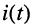или напряжение 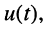то (7.1) будет представлять собой соответственно гармонический ток или гармоническое напряжение, причём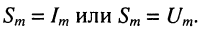

Гармоническое колебание определено полностью, если заданы все три его параметра: 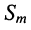— амплитуда, 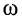— круговая частота,  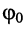— начальная фаза.

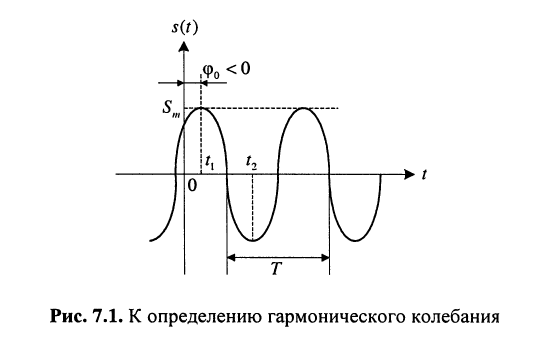
Рассмотрим смысл указанных параметров (рис. 7.1):

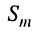   — амплитуда колебания — наибольшее по абсолютному значению отклонение колеблющейся величины; размерность амплитуды совпадает с размерностью колебания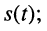

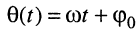— периодически изменяющийся аргумент функции 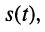называемый мгновенной фазой или просто фазой колебания; выражается в радианах (рад);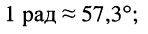

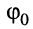  — начальная фаза (рад) — значение мгновенной фазы при 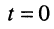, т. е. 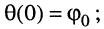начальная фаза может быть как положительной, так и отрицательной; начальная фаза определяет значение гармонического колебания в момент 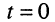и пропорциональна расстоянию от ближайшего максимума до оси ординат. При 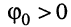максимум смещён влево от оси, а при 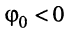— вправо; при 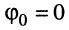максимум располагается на оси ординат;

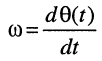- круговая частота (угловая скорость) — определяет скорость изменения фазы, выражается в радианах в секунду (рад/с),
т. е. круговая частота численно равна изменению мгновенной фазы за единицу времени (секунду).

Введём ещё два характерных для периодических колебаний параметра: период и частоту.

Т  — период колебания — наименьший интервал времени, через который процесс повторяется, а именно:

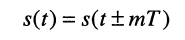       (7.2)

этому периоду соответствует изменение фазы на 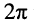радиан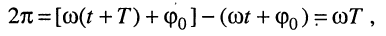

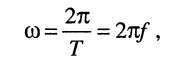      (7.3)

где величина

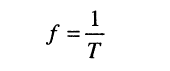       (7.4)

называется циклической частотой и измеряется в герцах (Гц).

В ряде практических задач требуется знать фазовые соотношения между гармоническими колебания одинаковой частоты. Фазовые соотношения характеризуют разностью фаз сравниваемых колебаний.

Пусть рассматриваются два колебания

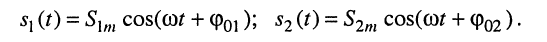      (7.5)

Тогда величина

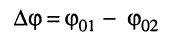
называется разностью фаз или сдвигом фаз этих колебаний. Если 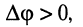то колебание 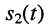отстаёт от колебания 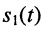по фазе на угол 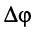; если  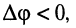то колебание 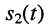опережает колебание 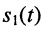на угол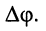

Если сдвиг фаз между двумя колебаниями равен 0, или 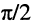  радиан, то говорят, что колебания происходят в фазе, противофазе или находятся в квадратуре соответственно.

При практических расчётах часто начальную фазу выражают в градусах (°). Поскольку 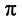соответствует 180°, то нетрудно получить соотношение

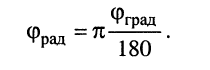    (7.6)

Линейные операции над гармоническими колебаниями

К линейным операциям над гармоническими колебаниями относятся: умножение на постоянное число (константу), дифференцирование, интегрирование и алгебраическое сложение гармонических колебаний одинаковой частоты. Результатом таких операций являются новые гармонические колебания той же частоты. Рассмотрим эти операции.

1. Умножение на константу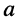

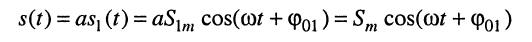
даёт новое гармоническое колебание, амплитуда которого отличается от амплитуды исходного колебания в 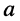раз

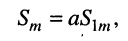
а фаза остаётся неизменной.

2. Дифференцирование

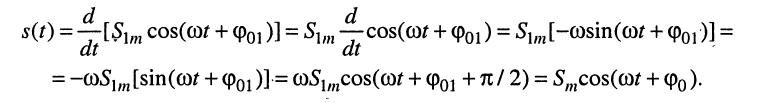
Из полученного результата следует, что при дифференцировании получается гармоническое колебание той же частоты; однако амплитуда и начальная фаза изменяются и оказываются равными

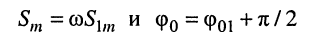
соответственно.

3.    Интегрирование

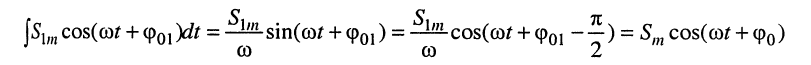
даёт гармоническое колебание той же частоты, но амплитуда и начальная фаза изменяются и оказываются равными:

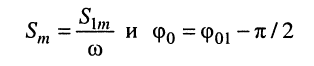
соответственно при условии равенства нулю постоянной интегрирования.

4.    Сложение (наложение, суперпозиция) гармонических колебаний одинаковой частоты

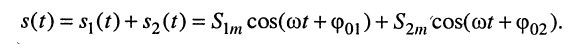
Воспользуемся известной формулой сложения аргументов

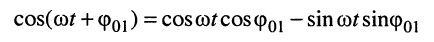
и представим гармонические колебания в виде:

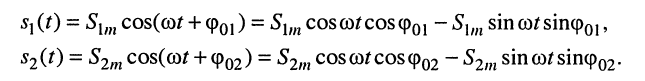
Складывая и группируя слагаемые, получаем:

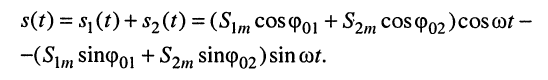     (7.7)

Обозначим в (7.7)

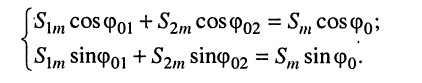     (7.8)

Подставляя (7.8) в (7.7)

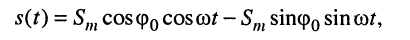
получаем

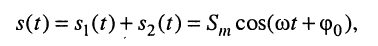      (7.8)

где при условии (7.8)

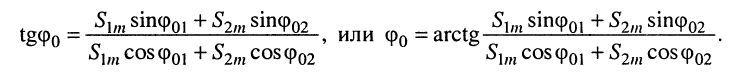        (7.9)

Остаётся найти амплитуду 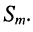 Для этого возведём в квадрат оба равенства (7.8) и извлечём корень из их суммы

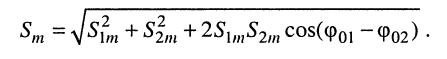        (7.10)

Помня, что 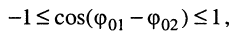исследуем результат (7.10) в зависимости от соотношения 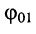и

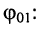
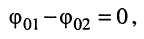•  т. е. колебания находятся в фазе: амплитуда результирующего колебания максимальна и равна сумме амплитуд составляющих колебаний

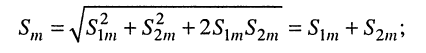
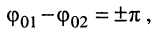•  т. е. колебания находятся в противофазе: амплитуда результирующего колебания минимальна и равна абсолютному значению разности амплитуд составляющих колебаний

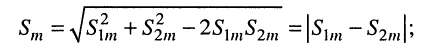
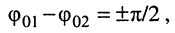• т. е. колебания находятся в квадратуре: амплитуда результирующего колебания равна корню квадратному из суммы квадратов амплитуд составляющих колебаний

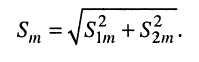
Выводы:

• линейные операции над гармонической функцией приводят лишь к изменению её амплитуды и начальной фазы;
• наложение двух гармонических колебаний равных частот образует гармоническое колебание той же частоты; амплитуда результирующего колебания зависит от соотношения начальных фаз слагаемых колебаний и лежит в пределах

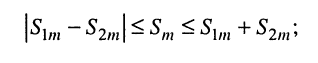
• наложение любого числа гармонических колебаний одной частоты образует гармоническое колебание той же частоты

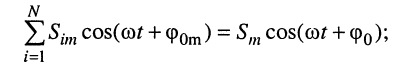
• амплитуду и начальную фазу результирующего колебания можно найти, последовательно применяя формулы сложения гармонических колебаний для каждой пары колебаний.

Энергетические характеристики гармонических колебаний

Кроме указанных в разд. 7.1.1 параметров, гармонические колебания описываются энергетическими характеристиками:

• мгновенной мощностью,
• средней мощностью,
• действующими (эффективными) значениями амплитуд напряжения и тока.

Мгновенная мощность гармонических колебаний при согласном выборе положительных направлений тока 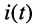и напряжения 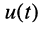определяется как произведение мгновенных значений тока и напряжения

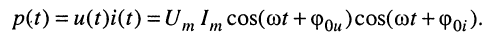
Заменив произведение косинусов на полусумму косинусов разности и суммы аргументов, получаем

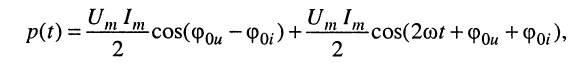       (7.11)

откуда следует, что потребляемая мгновенная мощность содержит постоянную составляющую (первое слагаемое, на графике Рср), относительно которой она колеблется с удвоенной частотой 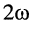(рис. 7.2).

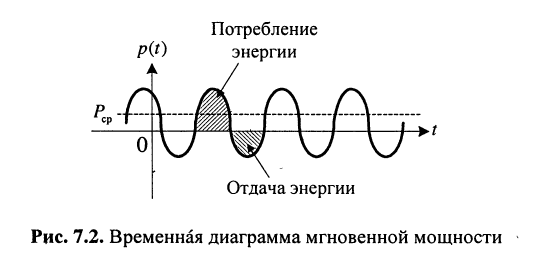
Положительным значениям мощности соответствует потребление цепью электрической энергии, а отрицательным значениям — отдача электрической энергии. В пассивных цепях это происходит за счёт энергии, запасаемой в конденсаторах (энергия электрического поля) и/или в индуктивностях (энергия магнитного поля). Для цепей, содержащих активные элементы, это означает, что цепь генерирует электрическую энергию.

Средняя (активная) мощность произвольных колебаний определяется как отношение энергии, подведённой к цепи за некоторый промежуток времени, к длительности этого промежутка 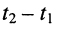при условии, что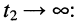

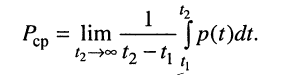   (7.12)

Для гармонических колебаний пределы интегрирования в (7.12) можно ограничить периодом колебания Т, полагая 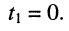. При этих условиях из (7.12) и (7.11) имеем:

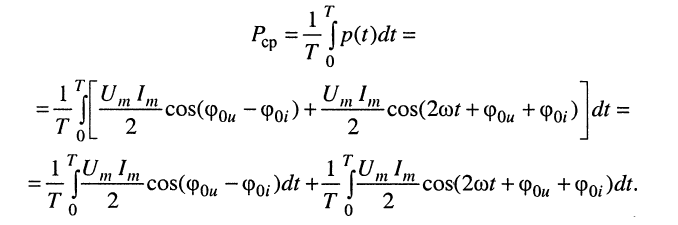         (7.13)

Левый интеграл в полученной сумме равен:

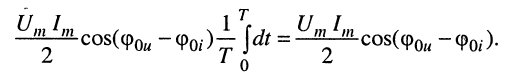
Обратимся к правому интегралу конечного выражения (7.13), представляющему собой интеграл от функции косинуса на периоде:

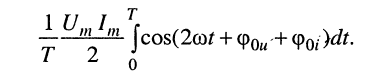
Найдём этот интеграл:
 

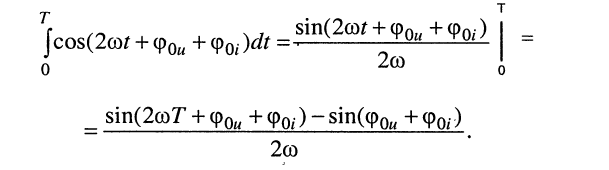
Числитель дроби равен нулю, поскольку, во-первых,

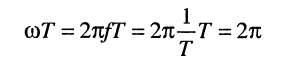
и, во-вторых, в силу периодичности функции синуса справедливы равенства:

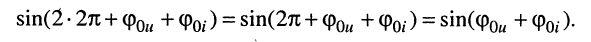
Таким образом, правый интеграл в (7.13) равен нулю, т. е. попутно доказано, что интеграл от функции косинуса за период равен нулю (это справедливо и для функции синуса).

Следовательно, средняя мощность гармонического колебания равна:

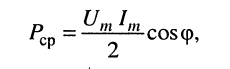     (7.14)

где 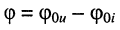; — разность фаз напряжения и тока на входе цепи, и является постоянной составляющей мгновенной мощности (7.11). Выражение (7.14) означает, что:

• средняя, или активная мощность пропорциональна амплитудам напряжения и тока и косинусу сдвига фазы между ними;
• чем меньше разность фаз, тем больше активная мощность;
•  для пассивных цепей согласно принципу сохранения энергии 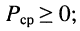при наличии зависимых источников это неравенство                  может не иметь силы;
• средняя мощность, потребляемая цепью, должна быть равна арифметической сумме средних мощностей, потребляемых в                      каждом элементе цепи

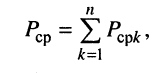
где 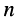— количество элементов в цепи, 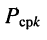— средняя мощность, потребляемая 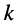-ым элементом.

На практике необходимо также знать среднеквадратичные значения произвольных напряжений и токов, которые определяются по формулам:

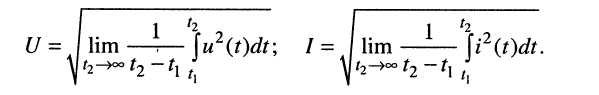     (7.15)

Отсюда для периодических, в том числе и гармонических, колебаний в соответствии с (7.13) имеем:

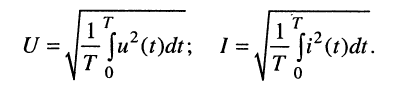       (7.16)

Подставляя в (7.16) выражения для мгновенных напряжений и токов

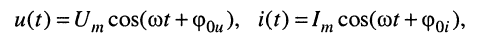
получаем:

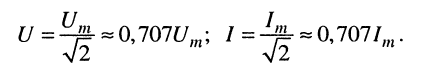     (7.17)

Среднеквадратические значения напряжений и токов называют действующими (эффективными). Они меньше амплитуд соответствующих колебаний в 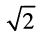раз.

Покажем вывод формул (7.17) на примере напряжения:

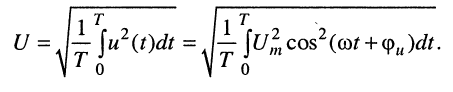
После замены:

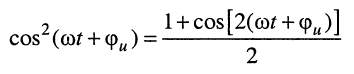
подкоренное выражение примет вид:

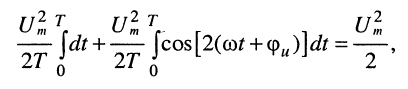
поскольку по доказанному ранее второй интеграл последней суммы равен нулю.

Действующие значения напряжения и тока позволяют записать среднюю мощность в форме:

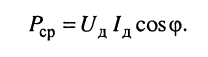
Символическое изображение гармонических колебаний

Гармонические напряжения и токи в линейной цепи находятся в результате решения задач анализа, которые даже для относительно простых цепей, как это будет видно из дальнейшего, оказываются достаточно трудоёмкими. На практике используются функциональные преобразования, в результате которых операции над исходными функциями заменяются более простыми операциями над некоторыми новыми функциями. Исходные функции называются оригиналами, а соответствующие им новые функции — изображениями или символами.

Решение любой задачи методом функционального преобразования состоит из трёх следующих основных этапов:

1. Прямого преобразования оригиналов к их изображениям (символам).
2. Вычисления изображений искомых функций по правилам операций над изображениями.
3. Обратного преобразования полученных изображений искомых функций к их оригиналам.

Рассматриваемое здесь функциональное преобразование, получившее название символического изображения гармонических колебаний, не является единственным; в лекции 16 будет рассмотрено более общее преобразование — преобразование Лапласа.

Идея символического изображения гармонических колебаний состоит в замене гармонических функций комплексными числами. Возможность такого изображения гармонических функций заложена в том, что в режиме гармонических колебаний все колебания имеют одну и ту же заранее известную частоту 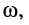равную частоте внешнего воздействия. Тогда гармоническое колебание

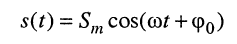
достаточно охарактеризовать только двумя вещественными числами: 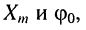 которые можно объединить в одно комплексное число и рассматривать его как символическое изображение гармонического колебания. А операции над числами проще операций над функциями.

Представим гармоническое колебание в виде действительной части новой комплексной функции, опустив для простоты записи индекс 0 при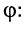

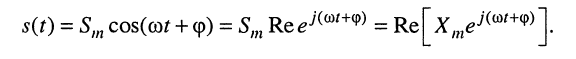       (7.18)

Тогда комплексная функция, стоящая в правой части равенства, может быть представлена как произведение некоторой комплексной функции на комплексную экспоненту

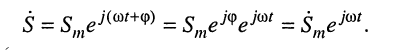
Определение:

Комплексная функция

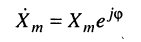       (7.19)

называется комплексной амплитудой или символическим изображением гармонического колебания: её модуль равен амплитуде 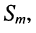 а аргумент — начальной фазе 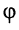гармонического колебания.

Восстановление 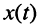по символическому изображению 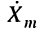ясно из соотношений (7.18) и (7.19). Например, гармоническое напряжение

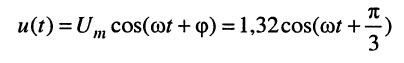
имеет комплексную амплитуду (символическое изображение) вида:

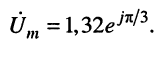
Соответствия между линейными операциями над гармоническими колебаниями и операциями над их символическими изображениями

1.    Умножение на константу:

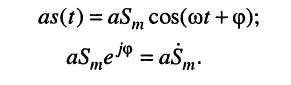
Полученная формула показывает, что умножению гармонического колебания на константу соответствует умножение на константу его комплексной амплитуды.

2.    Сложение: пусть гармоническое колебание 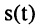представляет собой сумму N гармонических колебаний одинаковой частоты со, но имеющих разные амплитуды 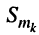и начальные фазы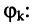

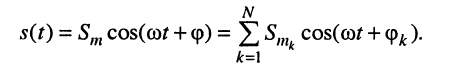
Применим к обеим частям данного равенства преобразование (7.41) с учётом того, что суммируемые колебания имеют одну и ту же частоту. Тогда получим:

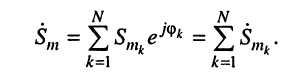
Следовательно, операции сложения (суммирования) гармонических колебаний соответствует операция сложения их комплексных амплитуд.

3.    Дифференцирование: дифференцируя функцию

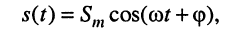
получаем

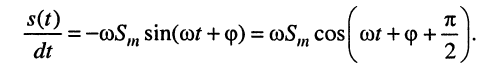
Комплексная амплитуда, т. е. символическое изображение найденной функции, оказывается такой:

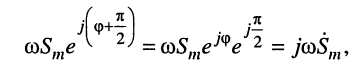
поскольку согласно формуле Эйлера (7.40)

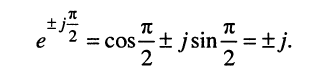
Следовательно, операции дифференцирования гармонического колебания соответствует операция умножения его комплексной амплитуды на оператор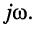

4. Интегрирование: интегрируя функцию

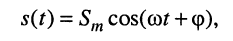
получаем

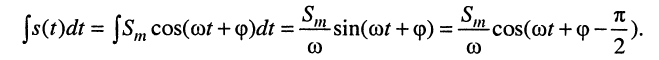
Символическое изображение этой функции имеет вид:

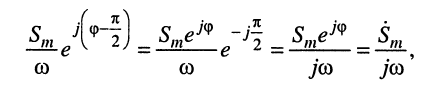
поскольку

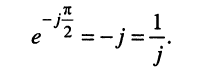
Следовательно, операции интегрирования гармонического колебания соответствует операция деления символического изображения на оператор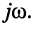

Заметим, что комплексные амплитуды напряжения и тока имеют вид:

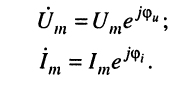
Например, мгновенному значению гармонического напряжения

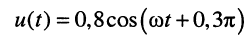
В соответствует комплексная амплитуда напряжения

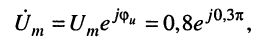
а комплексной амплитуде тока

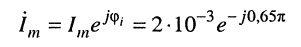
при известной круговой частоте 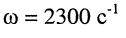соответствует мгновенное значение гармонического тока:

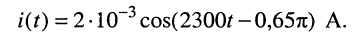
Законы Ома и Кирхгофа для комплексных амплитуд

Обозначим:

• комплексную амплитуду тока
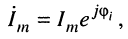
• комплексную амплитуду напряжения

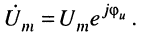
Покажем, что изученные ранее законы Ома и Кирхгофа справедливы и для комплексных амплитуд.

Закон Ома в символической форме:
для определения закона Ома необходимо установить связи между комплексными токами и напряжениями, действующими в некотором двухполюснике (рис. 7.3).

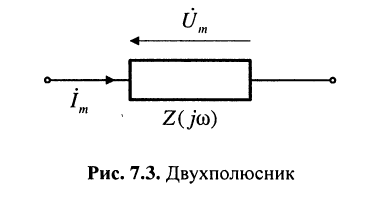
Введём следующие определения:

Комплексным сопротивлением двухполюсника 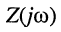называется отношение комплексных амплитуд напряжения и тока на входе двухполюсника

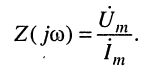     (7.20)

Комплексное сопротивление называют также комплексом полного сопротивления, или импедансом.

Комплексной проводимостью двухполюсника 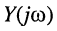называется отношение комплексных амплитуд тока и напряжения на входе двухполюсника

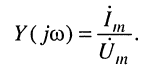     (7.21)

Комплексную проводимость называют также комплексом полной проводимости, или адмитансом.

Из определений следует соотношение:

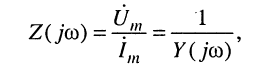          (7.22)

откуда вытекает, что комплексные амплитуды напряжений и токов на входе двухполюсника формально удовлетворяют закону Ома:

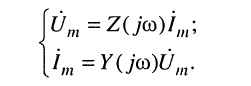      (7.23)

Комплексные сопротивления и проводимости двухполюсников представляют собой в общем случае комплексные величины, зависящие как от параметров цепи, так и от частоты воздействия.

Первый закон Кирхгофа в символической форме:
сумма комплексных амплитуд токов всех N ветвей, подключённых к каждому из узлов электрической цепи, равна нулю.

Действительно, для мгновенных значений токов имеем:

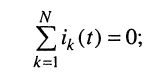
где 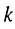— номер ветви, подключённой к рассматриваемому узлу. Тогда, заменяя мгновенные значения токов их комплексными амплитудами, согласно правилу сложения комплексных амплитуд получаем:

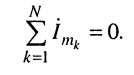
Второй закон Кирхгофа в символической форме.
сумма комплексных амплитуд напряжений на всех N ветвях, входящих в любой контур цепи, равна нулю.

Это показывается так же, как и для первого закона:

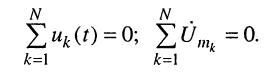
Комплексные сопротивления и проводимости

Поставим задачу установить связь между активными и реактивными составляющими комплексных сопротивлений и проводимостей, для чего подробнее рассмотрим комплексные амплитуды напряжения и тока (7.45).

Из комплексной амплитуды напряжения имеем:

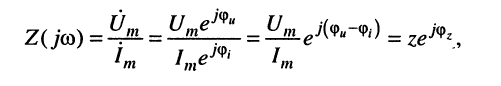     (7.24)

где

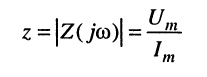
называется модулем комплексного сопротивления, или полным сопротивлением двухполюсника. Таким образом, полное сопротивление двухполюсника равно отношению амплитуды гармонического напряжения на зажимах двухполюсника к амплитуде гармонического тока, протекающего через эти зажимы.

Аналогично из соотношения

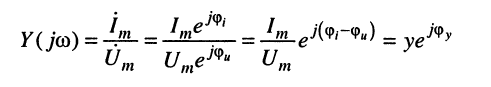
можно выделить модуль комплексной проводимости, или полную проводимость двухполюсника:

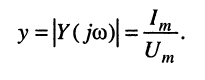
Замечание:

Аргументы комплексного сопротивления и комплексной проводимости у пассивных двухполюсников могут меняться только в пределах:

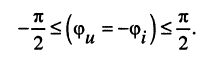
Для решения поставленной задачи представим комплексное сопротивление и комплексную проводимость в алгебраической форме:
 

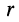— активная составляющая,

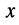 — реактивная составляющая комплексного сопротивления. Подобным образом для комплексной проводимости

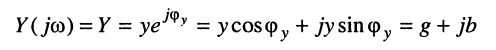       (7.27)

устанавливаются:

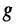    — активная составляющая,

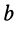   — реактивная составляющая комплексной проводимости.

Наконец, установим связь между активными и реактивными составляющими комплексных сопротивлений и проводимостей:

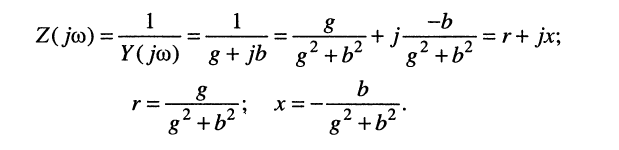      (7.28)

Аналогично получаем соотношения:

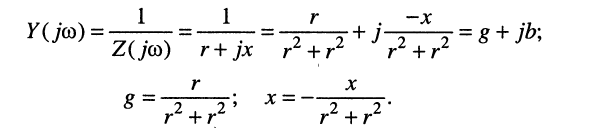     (7.29)

Выводы:

•  активные составляющие комплексных сопротивлений и проводимостей пассивных двухполюсников не могут принимать                      отрицательных значений;
• реактивные составляющие могут принимать как положительные, так и отрицательные значения: есл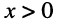и и 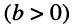                              сопротивление (проводимость) имеет индуктивный характер, в противном случае — ёмкостной;
• если колебания напряжения и тока происходят в фазе 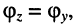двухполюсник обладает чисто активным сопротивлением                        (проводимостью).

Комплексные числа и операции над ними

Рассмотрим всевозможные пары действительных (обычных) чисел, взятых в определённом порядке. Каждую такую упорядоченную пару 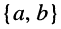называют комплексным числом, обозначают одной буквой (например, 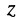) и записывают в виде

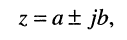
где символ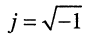 отделяет одно число из пары от другого; знаки ± указывают на то, что два действительных числа объединяются в нечто единое. Число а называется действительной частью 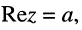число 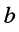— мнимой частью 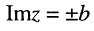комплексного числа. Комплексные числа 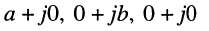можно записывать как 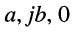соответственно. При этом:

• комплексное число вида 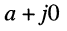называется действительным (вещественным);
• комплексное число вида 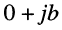называется чисто мнимым;
• число 0— единственное комплексное число, которое является одновременно и действительным, и мнимым;
• два комплексных числа, которые отличаются только знаком мнимой части, называются комплексно-сопряжёнными; число, комплексно-сопряжённое с числом 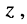обозначают 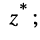таким образом, если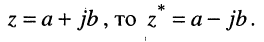

Запишем формулы для натуральных степеней числа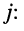

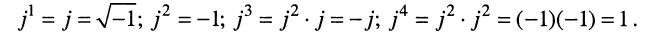 Из (7.30) видно, что при возведении числа j в степень п наблюдается периодичность значений степени, а именно: из равенства 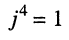следует, что если  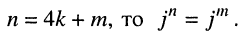Иными словами: чтобы найти  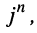достаточно возвести 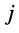в степень, показатель которой равен остатку от деления 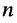на 4.

Арифметические действия над комплексными числами

1. Два комплексных числа считаются равными, если равны их действительные и мнимые части.
2. Сложение, вычитание и умножение комплексных чисел следует производить так, словно это многочлены относительно буквы 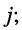при этом произведение 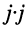заменяется на -1.

Пусть 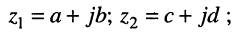тогда на основании записанных правил получаем:

•    равенство 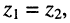если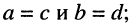

•    сумму 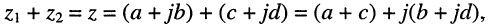или в общей форме:

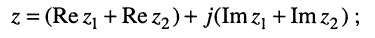      (7.31)

•    разность:

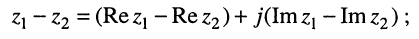      (7.32)

•    произведение:

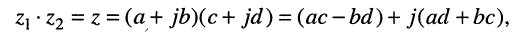
или в общей форме

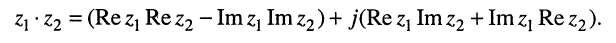    (7.33)

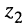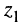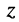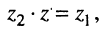3.    Деление комплексных чисел определяется как действие, обратное умножению: частным от деления комплексного числа на число называют такое число , что т. е.

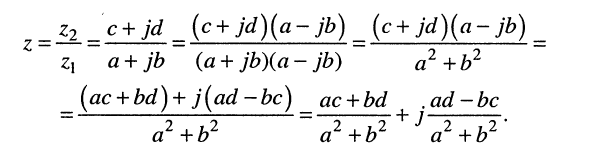     (7.34)

4. Полезные тождества:

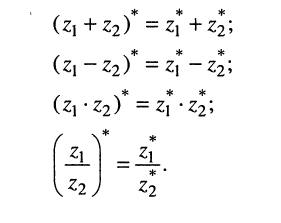  (7.35)

Геометрический смысл комплексных чисел

Как известно, положение точки Z  на координатной плоскости задаётся двумя действительными числами, являющимися координатами этой точки, что записывается в виде 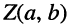, но точно так же задаётся и комплексное число z. Таким образом, между координатами точки и комплексным числом существует однозначное соответствие, а именно: точке 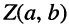на плоскости соответствует комплексное число 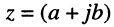; это комплексное число назовём комплексной координатой, а саму плоскость — комплексной плоскостью, по оси абсцисс которой откладываются значения действительной части 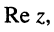а по оси ординат — значения мнимой части 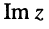комплексного числа  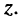Эти оси комплексной плоскости называются действительной и мнимой соответственно (рис. 7.4, а). Комплексной координатой начала координат О является число 0 (нуль).

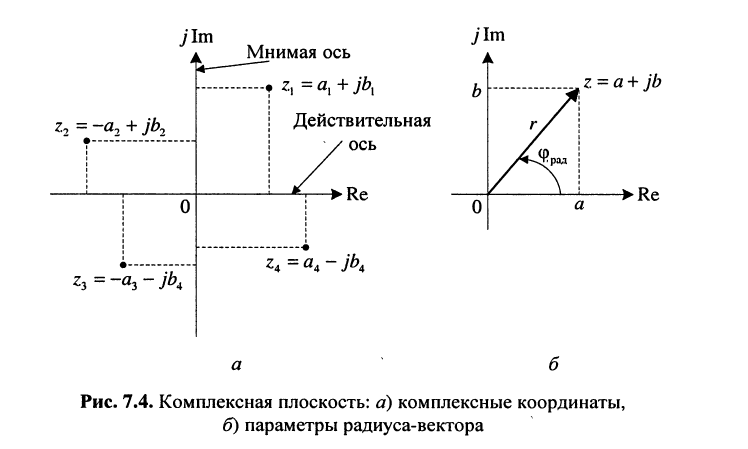
С другой стороны, на той же комплексной плоскости выберем произвольный радиус-вектор 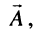для простоты выходящий из начала координат. Тогда конец его будет иметь координату 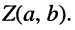Комплексное число  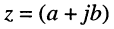называется комплексной координатой вектора А. Длина  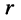этого вектора (расстояние от начала координат до точки 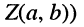называется модулем комплексного числа .

 

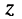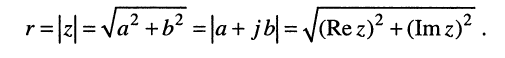
Угол 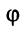наклона вектора к действительной оси называется аргументом 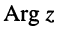числа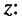

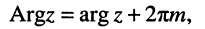
где 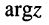называется главным значением аргумента (главным аргументом); главное значение аргумента удовлетворяет неравенствам:

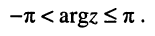      (7.37)

Из рис. 7.4, б следует, что

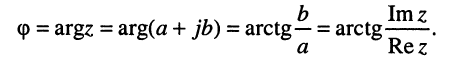      (7.38)

Аргумент считается положительным при отсчёте против часовой стрелки и отрицательным — при отсчёте в противоположном направлении.

Формулы Эйлера и Муавра

Вновь обратимся к рис. 7.4, б и найдём значения 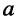и 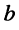через значения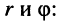

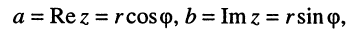
которые позволяют записать комплексное число 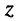 в тригонометрической форме:

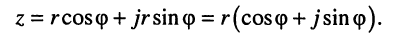      (7.39)

В 1743 году Эйлер предложил обозначить

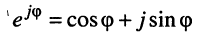       (7.40)

и назвать полученное соотношение мнимой экспонентой. Тогда комплексное число z можно записать в показательной (полярной) форме

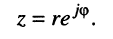      (7.41)

Из (7.40) следуют две формулы, выражающие через 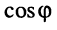и 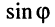мнимые экспоненты. Заменяя в (7.40) 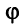на 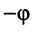, имеем:

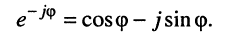     (7.42)

Складывая и вычитая почленно (7.40) и (7.42), получаем:

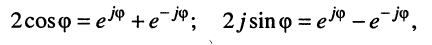   (7.43)

откуда следуют интересующие нас формулы:
 

Заметим также, что модуль комплексной экспоненты равен единице; действительно:

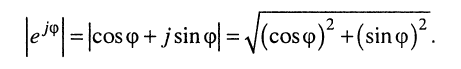      (7.44)

Найдём выражение, соответствующее степени 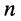мнимой экспоненты (7.40):

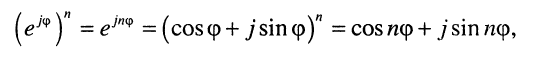   (7.45)

откуда следует:

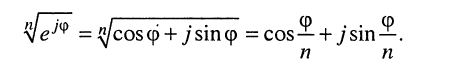   (7.46)

Формулы (7.45) и (7.2) называются формулами Муавра.