Гармонические колебания в колебательном контуре

Содержание:

Режим гармонических колебаний в последовательном колебательном контуре:

Определение:

Последовательным колебательным контуром называется электрическая цепь, состоящая из последовательно соединённых элементов резистивного сопротивления R, индуктивности L и ёмкости С (рис. 11.1).

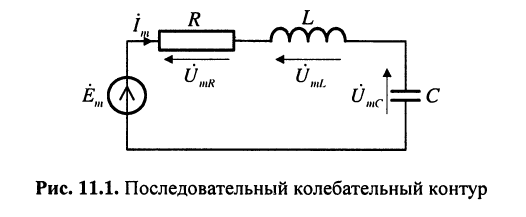
Последовательный контур характеризуется своими первичными и вторичными параметрами:

1. первичными параметрами называют значения элементов R, L и С, причём резистивное сопротивление R характеризует потери в          контуре;
2. вторичными параметрами, зависящими от первичных, называют:

• добротность
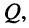
• резонансную частоту
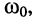
• волновое (характеристическое) сопротивление
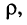
• затухание

Роль и свойства вторичных параметров изучаются в разд. 11.1.2.

Ток в последовательном контуре

Задача 11.1.

Найти закон изменения тока 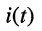в последовательном контуре, к которому приложено гармоническое напряжение частоты со с комплексной амплитудой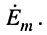

Решение.

Комплексное сопротивление последовательного контура

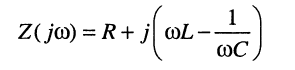      (11.1)

позволяет по закону Ома вычислить комплексную амплитуду тока:

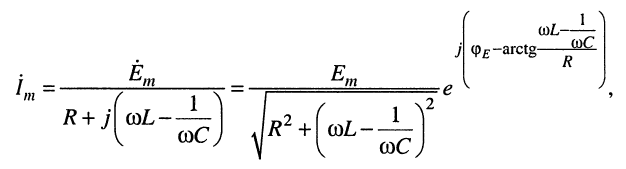       (11.2)

откуда амплитуда тока

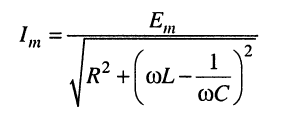      (11.3)

и его начальная фаза

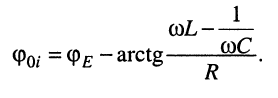       (11.4)

В дальнейших рассуждениях ничего не изменится, если в (11.4) положить начальную фазу гармонического напряжения равной нулю 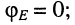при таком предположении начальная фаза тока оказывается равной:

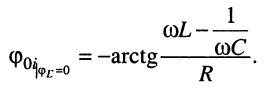      (11.5)

Выражения (11.3) и (11.5) позволяют записать формулу тока в последовательном контуре:

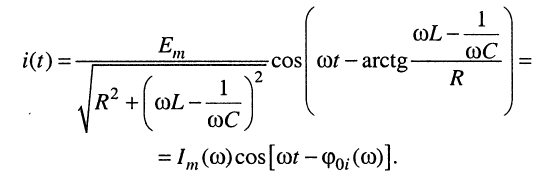        (11.6)

Полученное решение показывает, что амплитуда 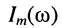и начальная фаза 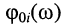тока зависят от значений элементов (R, L, С), составляющих контур, и от частоты гармонического воздействия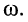

По этой причине значения элементов R, L, и С называются первичными параметрами контура.

Задача 11.2.

Найти характер зависимости амплитуды тока (11.3) в последовательном контуре от частоты 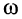гармонического воздействия.

Решение. Из (11.3) ясно, что амплитуда тока максимальна

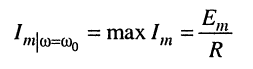    (11.7)

на той частоте 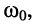на которой второе слагаемое подкоренного выражения равно нулю

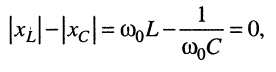
т. е. когда полные реактивные сопротивления контура, оказываются равными друг другу:

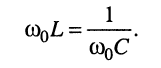   (11.8)

Определим частоту 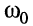, на которой выполняется это условие. Из равенства (11.8) следует:

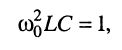
откуда

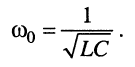      (11.9)

Заметим, что сопротивление контура (11.1) на частоте 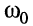чисто активно:

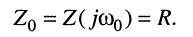    (11.10)

Активность сопротивления контура означает, что на частоте :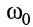

• амплитуда тока максимальна (11.8);
• ток в цепи 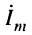и напряжение на сопротивлении 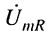совпадают по фазе, что видно из (11.6), поскольку
• амплитуда тока в контуре 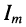тем меньше, чем больше частота 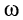отличается от 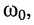при чём пр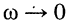и и амплитуда тока        в контуре стремится к нулю:

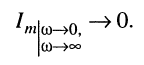
Из сказанного можно сделать вывод:

частотно зависимая амплитуда тока в последовательном колебательном контуре при приближении частоты 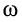к 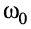резко возрастает; такое явление резкого возрастания амплитуды реакции при приближении частоты 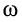к 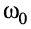называется резонансом, а сама частота 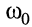— резонансной частотой.

В разд. 11.1.2 представлены более общие определения резонанса и резонансной частоты.
 

Свойства последовательного контура при резонансе

Определение:

Под резонансом понимают такое состояние электрической цепи, при котором её комплексное входное сопротивление имеет чисто резистивный (активный) характер, а потому разность фаз между током и напряжением на входе оказывается равной нулю.

Определение:

Резонансной называется частота, при которой входное сопротивление контура имеет чисто резистивный характер.

Резонанс напряжений

Рассмотрим значения амплитуд напряжений на индуктивности и ёмкости контура (рис. 11.1) при 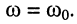Исходя из справедливости закона Ома для комплексных амплитуд, запишем выражение для комплексной амплитуды напряжения на индуктивности:

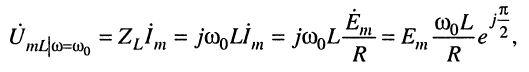
откуда амплитуда напряжения

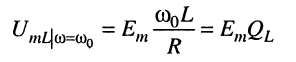     (11.11)

и фаза

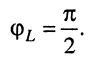       (11.12)

Аналогично можно записать выражения для амплитуд и фазы напряжения на ёмкости:

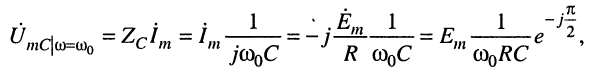
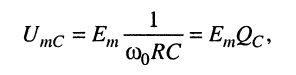   (11.13)

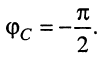    (11.14)

Заметим, что величины 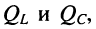введённые в (11.11) и (11.13), равны друг другу вследствие равенства полных реактивных сопротивлений на частоте резонанса (11.8), т. е.

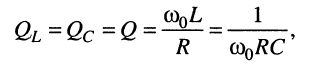      (11.15)

поэтому напряжения на ёмкости и на индуктивности равны по амплитуде, но, согласно (11.12) и (11.14), противоположны по фазе

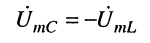
и потому компенсируют друг друга.

Иначе говоря, на частоте резонанса 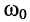колебания напряжений на индуктивности и ёмкости находятся в противофазе, поскольку

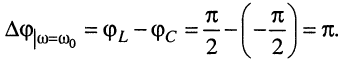
Такой вид резонанса называют резонансом напряжений.

Вторичные параметры

Величина 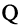называется добротностью последовательного контура; она показывает, во сколько раз на частоте резонанса 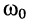амплитуда напряжения на индуктивности и на ёмкости превышает амплитуду задающего напряжения

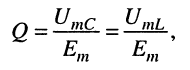       (11.16)

или, согласно (11.15), во сколько раз на частоте резонанса 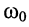полное сопротивление индуктивности 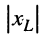и полное сопротивление ёмкости 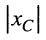превышают величину активного сопротивления R. Величину

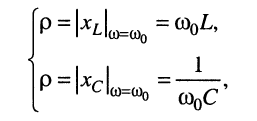       (11.17)

равную полному сопротивлению индуктивности и полному сопротивлению ёмкости на частоте резонанса, называют характеристическим, или волновым, сопротивлением контура. Причём значение 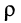не зависит от частоты и определяется только параметрами реактивных элементов контура

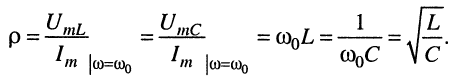       (11.18)

Справедливость последнего равенства показывается очень просто. Поскольку

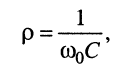
то резонансная частота равна:

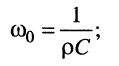
подставим полученное значение 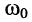в выражение для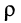

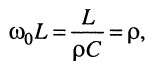
откуда имеем:

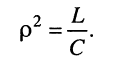
Используя равенства (11.15), (11.17) и (11.18), нетрудно выразить добротность контура через параметры его элементов:

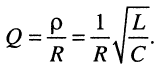        (11.19)

Как правило, значение добротности колебательных контуров достаточно велико и может составлять несколько сотен, поэтому на частоте резонанса напряжение на реактивных элементах может существенно превышать приложенное к контуру напряжение.

Величина, обратная добротности,

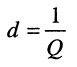     (11.20)

называется затуханием контура.

Резонансную частоту 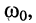волновое (характеристическое) сопротивление 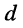, добротность 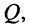затухание 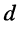называют вторичными параметрами контура, поскольку они полностью определяются первичными параметрами.

Частотные характеристики последовательного контура

 Комплексная частотная характеристика по току:

Выберем в качестве реакции ток в контуре; тогда КЧХ по току согласно определению

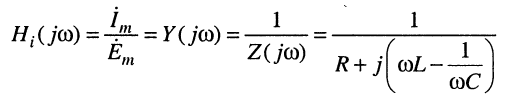        (11.21)

имеет размерность проводимости.

Преобразуем знаменатель КЧХ, для чего воспользуемся определением резонансной частоты и добротности:
 

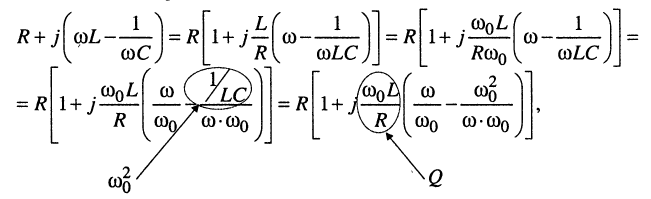
откуда

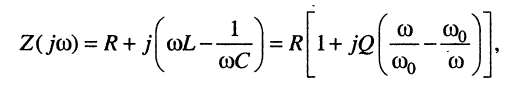
и после подстановки в (11.20) имеем:

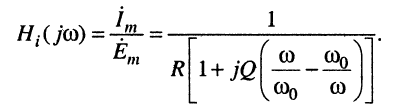        (11.22)

Отсюда для последовательного колебательного контура получаем амплитудно-частотную характеристику по току

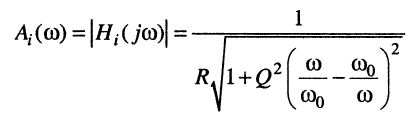      (11.23)

и фазочастотную характеристику

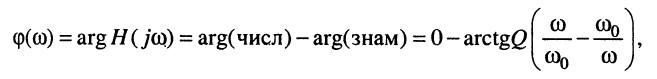
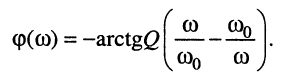      (11.24)

При этом нормированная АЧХ имеет вид:

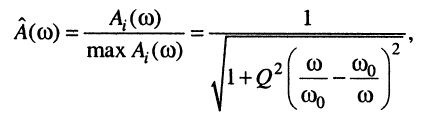       (11.25)

где

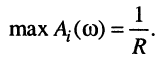
Исследуем частотные характеристики при различных частотах относительно

частоты резонанса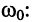

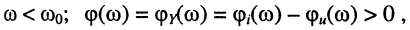     это значит, что сопротивление контура имеет индуктивный характер: ток отстаёт по              фазе от приложенного напряжения;

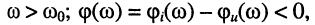     это значит, что сопротивление контура имеет ёмкостной характер: ток опережает по фазе                          приложенное напряжение;

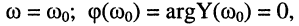     это значит, что проводимость (сопротивление) контура чисто активна(о) и мииимальна(о), что подтверждает сделанный ранее вывод.

Резонансные характеристики последовательного контура

Зависимость амплитуды (или действующего значения) тока от частоты

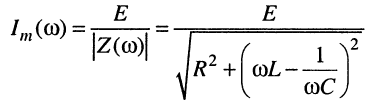         (11.26)

называется резонансной кривой тока, которая изображена на рис. 11.2.

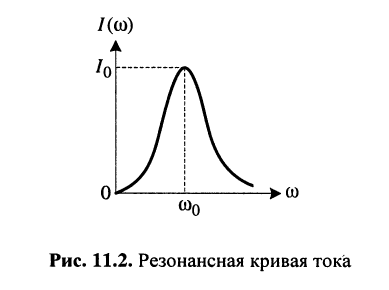
Значения напряжений на реактивных элементах нетрудно определить в соответствии с законом Ома, если воспользоваться выражением (11.26):
на индуктивности

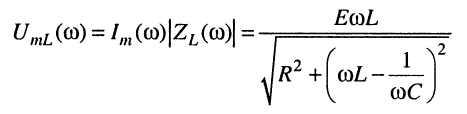        (11.27)

и на емкости

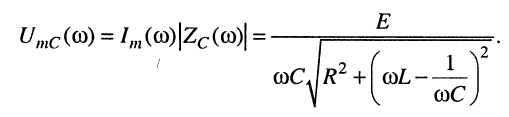        (11.28)

Зависимости (11.25)—(11.28) называются резонансными характеристиками тока и напряжений.

Обычно выходное напряжение снимается с ёмкости или индуктивности, поэтому практический интерес представляют КЧХ по напряжению относительно элементов С и L, которые по определению имеют вид:

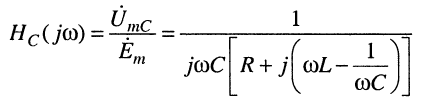         (11.29)   

    и 

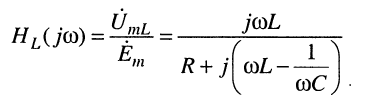    (11.30)

соответственно.

Из (11.29) и (11.30) легко получить выражения для соответствующих АЧХ и ФЧХ последовательного контура:

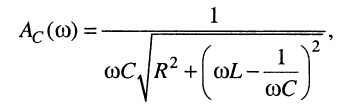      (11.31)

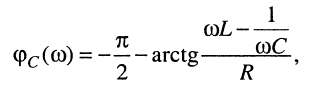      (11.32)
 

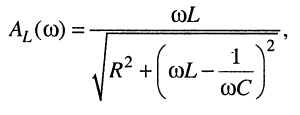          (11.33)
 

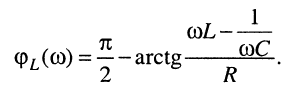        (11.34)

На рис. 11.3 изображены АЧХ и ФЧХ последовательного контура, описываемые выражениями (11.31)—(11.34). Из этих выражений и графиков следует:

при 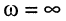АЧХ принимают значения: 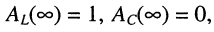а ФЧХ равны: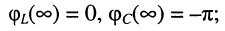   

  при 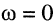АЧХ принимают значения: 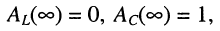а ФЧХ равны: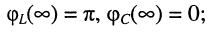   

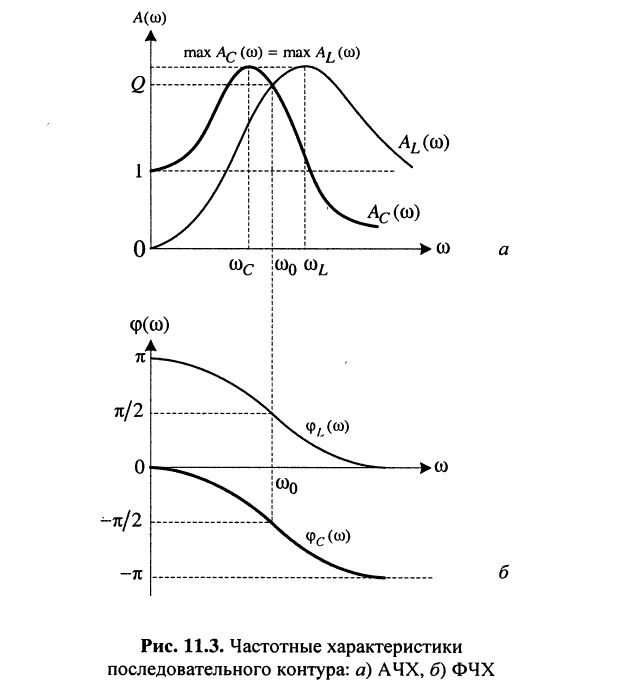
на частоте резонанса 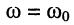имеем резонанс напряжений, причём согласно (11.19) получаем:

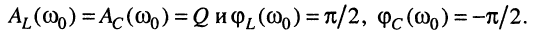      (11.35)

Кроме того, АЧХ 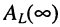и 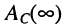имеют максимумы на частотах 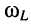и 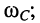 частоты нетрудно найти, взяв производные от 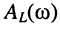и 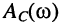по частоте:

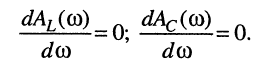
Тогда получим:

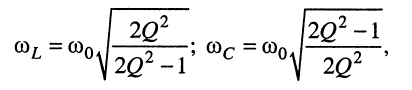        (11.36)

откуда ясно, что:

  с ростом добротности контура частоты 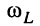и 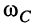сближаются с частотой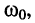

  на этих частотах АЧХ 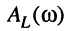  и 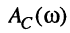принимают равные максимальные значения

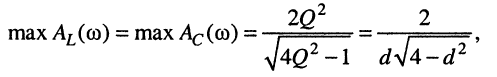      (11.37)

которые растут с ростом добротности (уменьшением затухания d).

Режим гармонических колебаний в параллельном колебательном контуре

Параметры параллельного контура:

Параллельным колебательным контуром называется электрическая цепь, состоящая из параллельно соединённых элементов индуктивности L, ёмкости С и резистивного элемента G (рис. 12.1). Резистивный элемент G характеризует потери в контуре.

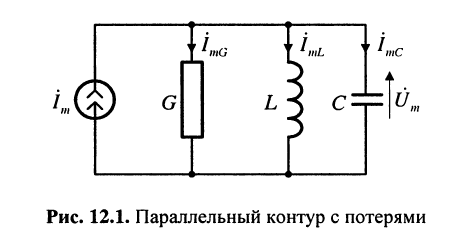
Изображённый на рис. 12.1 параллельный контур представляет собой схему замещения, в которой значения элементов G и С определены с учётом внутренней проводимости генератора тока 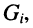собственной проводимости контура 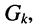проводимости нагрузки 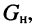собственной ёмкости контура 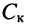и паразитных ёмкостей 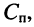шунтирующих контур, т. е.

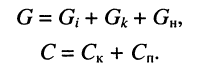
Задача 12.1.

Найти закон изменения напряжения 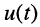на зажимах контура, на входе которого действует источник тока

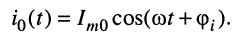
Решение. На основании закона Ома, исходя из комплексной амплитуды задающего тока

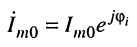
и комплексной проводимости параллельного контура

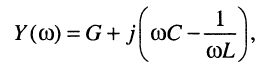        (12.1)

получим комплексную амплитуду напряжения

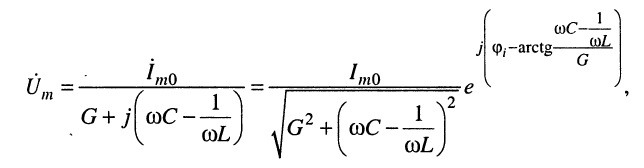             (12.2)

откуда амплитуда гармонического напряжения

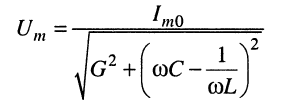    (12.3)

и его начальная фаза при условии 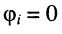(что не ведёт к потере общности)

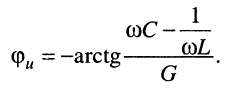          (12.4)

Выражения (12.3) и (12.4) позволяют записать формулу напряжения на зажимах параллельного контура

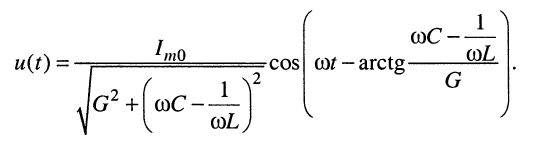                                                                     (12.5)

Полученное решение показывает, что амплитуда и начальная фаза напряжения полностью определяются первичными параметрами контура (G, L, С) и частотой гармонического воздействия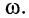

Задача 12.2.

Найти зависимость амплитуды напряжения (12.3) в параллельном колебательном контуре от частоты со гармонического воздействия.

Решение. Из (12.3) ясно, fro амплитуда напряжения максимальна на той частоте, на которой второе слагаемое подкоренного выражения равно нулю

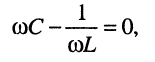
т. е., как и в случае последовательного контура, на частоте резонанса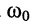

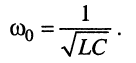
При этом полные реактивные проводимости контура оказываются равными друг другу

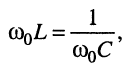
сопротивление (проводимость) контура на частоте 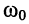чисто активно

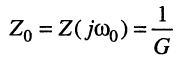
и максимум амплитуды напряжения на зажимах контура равен

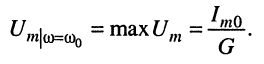
Свойства параллельного контура при резонансе

Рассмотрим амплитуды токов в реактивных элементах контура 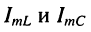и начальные фазы 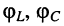этих токов на частоте
резонанса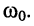

Комплексная амплитуда тока в индуктивности

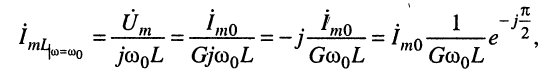
откуда амплитуда тока имеет вид:

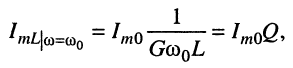        (12.6)

а начальная фаза составляет

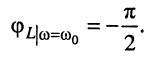        (12.7)

Аналогично для тока в ёмкости нетрудно получить:

комплексную амплитуду тока

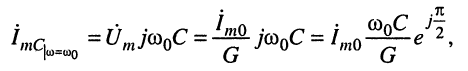
    амплитуду тока

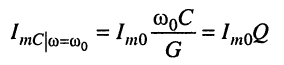       (12.8)

    и её начальную фазу

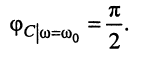       (12.9)

Выражения (12.6) и (12.8) позволяют записать формулу добротности параллельного контура

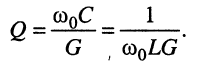      (12.10)

Из сравнений (12.6) с (12.8) и (12.7) с (12.9) замечаем, что:

    на частоте резонанса амплитуды токов в реактивных элементах контура оказываются равными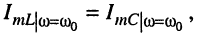  

    начальные фазы токов отличаются на 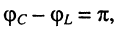т. е. токи находятся в противофазе.

Выводы:

    на резонансной частоте токи в реактивных элементах компенсируют друг друга, причём амплитуды этих токов в 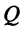раз превышают амплитуду задающего тока. Такое явление называется резонансом токов;

    на резонансной частоте отношение амплитуды напряжения на зажимах контура к току в реактивных элементах называется волновым (характеристическим) сопротивлением контура

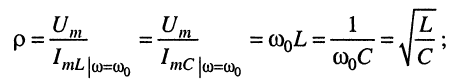         (12.11)

    используя равенства (11.15), (11.17) и (11.18), нетрудно выразить добротность контура через параметры его элементов:

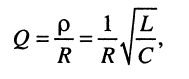
Величина, обратная добротности,

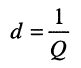     (12.13)

называется затуханием контура;

формулы волнового сопротивления (12.11), добротности (12.12) и затухания (12.13) параллельного колебательного контура полностью совпадают с формулами этих же параметров для последовательного колебательного контура (11.18), (11.19) и (11.20).

Как и в случае последовательного колебательного контура, резонансную частоту 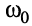, волновое (характеристическое) сопротивление 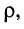добротность 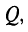затухание 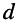называют вторичными параметрами контура, поскольку они полностью определяются первичными параметрами.

Резонансные характеристики параллельного контура

На практике наибольший интерес представляет напряжение u(t) на зажимах колебательного контура (см. рис. 12.1), которое и определим в качестве реакции. Тогда комплексная частотная характеристика по напряжению

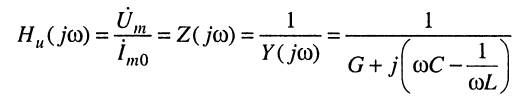
имеет размерность сопротивления.

Преобразуем знаменатель КЧХ (рис. 12.2), для чего, как и в случае последовательного контура, воспользуемся определением резонансной частоты и добротности

откуда комплексная проводимость

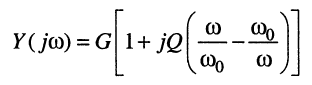
и после подстановки в (12.14) получаем выражения для КЧХ, АЧХ и ФЧХ параллельного колебательного контура:

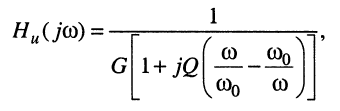      (12.15)
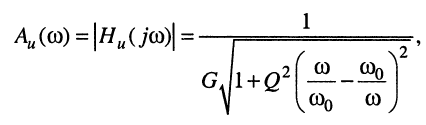     (12.16)

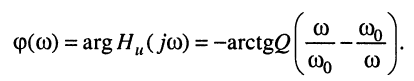     (12.17)

Комплексную (12.15) и амплитудно-частотную (12.16) характеристики называют резонансными характеристиками параллельного колебательного контура.

Исследуем частотные характеристики при различных частотах относительно частоты резонанса 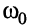, при этом будем пользоваться нормированной АЧХ

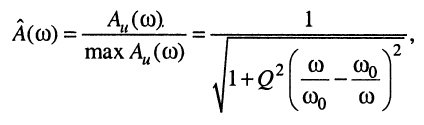              (12.18)

которая также относится к резонансным характеристикам.

Анализ соотношений (12.17), (12.18) и рис. 12.3 позволяет сделать следующие выводы.

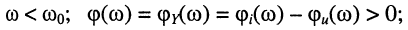   это значит, что сопротивление контура имеет индуктивный характер — напряжение                опережает по фазе задающий ток;

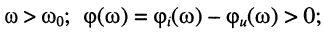     это значит, что сопротивление контура имеет ёмкостной характер — напряжение отстаёт по                фазе  от задающего тока;
 

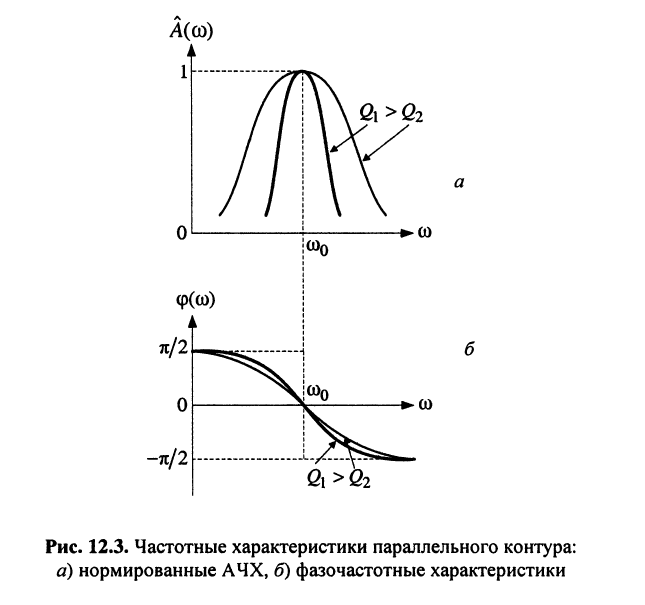
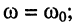АЧХ проходит через максимум, а ФЧХ — через нуль 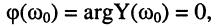это значит, что сопротивление (проводимость) контура чисто активно и максимально, что подтверждает сделанный ранее вывод;

в области малых частот, когда полное сопротивление элемента индуктивности может стать как угодно малым и, шунтируя остальные элементы контура, будет определять частотные характеристики контура, а именно:

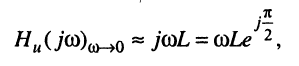
или

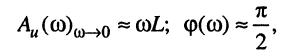
причём

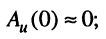
в области высоких частот, когда 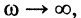полное сопротивление элемента ёмкости может стать как угодно малым и, шунтируя остальные элементы контура, будет определять частотные характеристики контура, а именно:

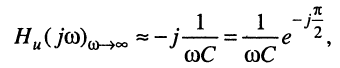
или

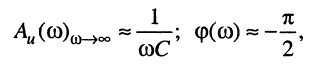
причём

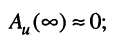
 изменение добротности контура не влияет на характер частотных зависимосте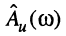й и 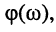но существенно влияет на их форму; так, с увеличением добротности АЧХ становится более узкой (возрастает крутизна АЧХ).

Свойства частотных характеристик колебательных контуров

В лекциях 11 и 12 были подробно рассмотрены АЧХ и ФЧХ последовательных и параллельных контуров. И те и другие контуры находят широкое применение в устройствах телекоммуникации для селекции, или фильтрации, разнообразных сигналов по частоте, поэтому проведём более детальное исследование частотных характеристик контуров.

Общие свойства частотных характеристик

Рассмотрим резонансные характеристики контуров, для чего обратимся к формулам нормированных АЧХ (11.25), (12.18) и формулам ФЧХ (11.24) и (12.17). Видно, что они внешне ничем не отличаются, что позволяет весь последующий анализ вести одновременно как для последовательного, так и для параллельного контура по формулам:

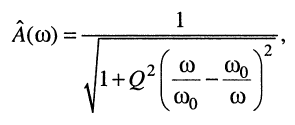         (13.1)

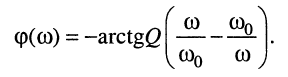          (13.2)

Понятия о расстройках колебательного контура

Степень отклонения режима колебательного контура от резонанса зависит от частоты со и оценивается расстройками. Различают:

абсолютную расстройку

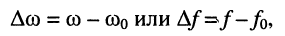       (13.3)

относительную расстройку

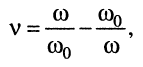        (13.4)

обобщённую расстройку

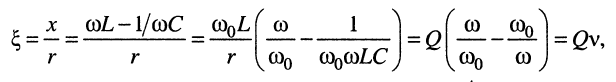     (13.5)

причём при 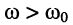обобщённая расстройка 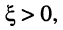а при 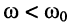обобщённая расстройка 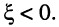То же самое относится и к другим расстройкам.

Тогда АЧХ и ФЧХ последовательного и параллельного контуров можно записать в более компактном виде:

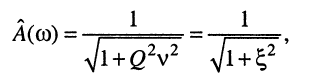    (13.6)

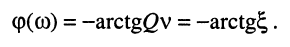       (13.7)

Свойства резонансной частоты

Свойство 1.

Резонансная частота 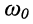контура является средним геометрическим для любой пары частот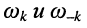

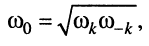       (13.8)

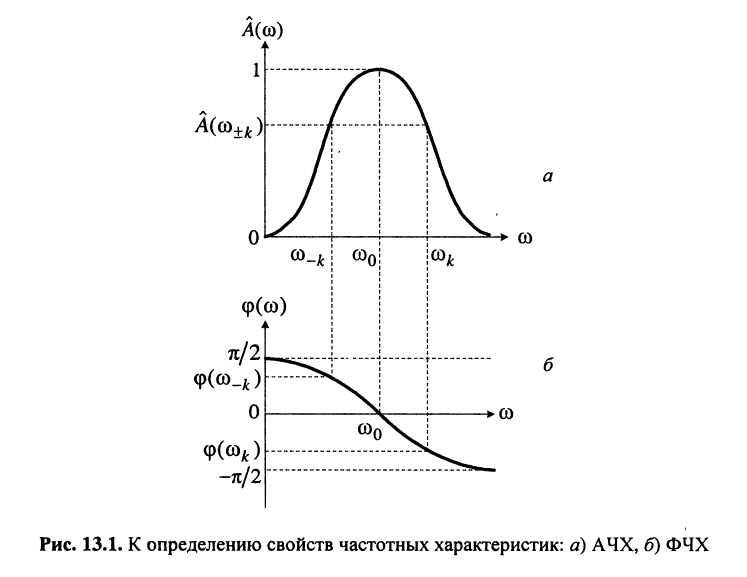
на которых АЧХ принимает равные значения (рис. 13.1).

Иначе говоря, частоты, на которых А ЧХ принимает равные значения, обладают геометрической симметрией относительно резонансной частоты.

Доказательство. Равенство АЧХ на частотах 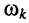и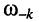

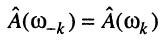
означает, что обобщённые расстройки на этих частотах должны быть равны по модулю и противоположны по знаку. Это позволяет записать

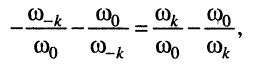
откуда имеем:

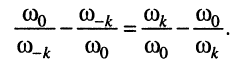
Проведя следующие несложные преобразования:

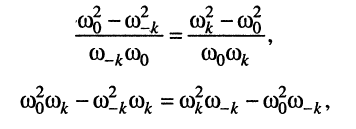
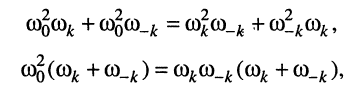
получаем:

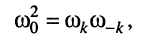
откуда

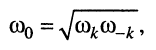
что и требовалось доказать.

Свойство 2.

Значения ФЧХ на частотах 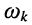и 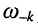равны по модулю и противоположны по знаку.

Действительно, согласно (13.2) на этой паре частот в силу нечётности ФЧХ получаем:

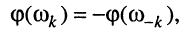
что показано на рис. 13.1, б.

Свойство 3.

Для пары частот 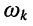и 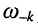 которые близки к резонансной частоте и на которых АЧХ принимает равные значения, резонансная частота 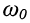с высокой степенью точности представляется полусуммой этих частот:

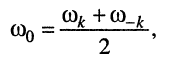     (13.9)

т. е. относительно таких частот резонансная частота обладает арифметической симметрией.

Доказательство. Выразим относительную расстройку v через абсолютную расстройку

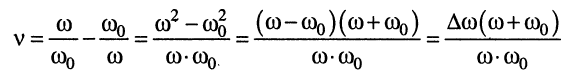         (13.10)

и исследуем полученный результат при условии, что со не слишком сильно отличается от 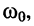т. е. при условии  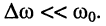- Тогда формула (13.10) получает вид:

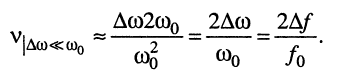       (13.11)

Последнее позволяет записать приближённые формулы для АЧХ и ФЧХ контура вблизи резонансной частоты:

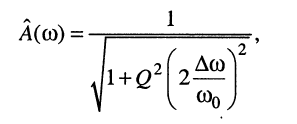     (13.12)
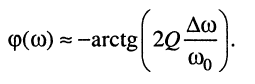       (13.13)

Если теперь вновь, как это было выполнено ранее, приравнять значения АЧХ на частотах 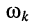и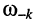

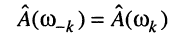
и учесть знаки абсолютных расстроек (13.3), то получим пропорцию:

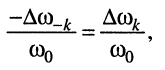
из которой следуют равенства:

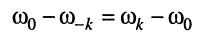
и

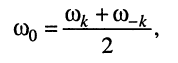
что и требовалось доказать.

Избирательность простейших колебательных контуров

Вид амплитудно-частотных характеристик, изображённых на рис. 12.2,а  и рис. 13.1, указывает на то, что амплитуда реакции контура на гармоническое воздействие существенно зависит от частоты, а именно:

• на резонансной частоте она достигает максимума;
• в узком диапазоне частот, близких к резонансной частоте, она близка к максимальной;
• становится тем меньшей, чем больше частота отклоняется от резонансной.

Полоса пропускания

Понятно, что если на колебательный контур одновременно подать гармонические колебания различных частот с одинаковыми амплитудами, то на выходе контура амплитуды колебаний, частоты которых близки к резонансной 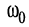, значительно превысят амплитуды колебаний с частотами, существенно отличающимися от резонансной частоты. Иначе говоря, контур пропускает (выделяет) колебания одних частот и не пропускает (задерживает) колебания других частот. Таким свойством могут обладать и более сложные электрические цепи.

Определение:

Частотной избирательностью, или селективностью, называется способность электрической цепи выделять колебания определённого диапазона частот; при этом сама цепь называется избирательной, или селективной.

Для количественной оценки селективных свойств контуров используются следующие параметры: полоса пропускания, ширина полосы пропускания, неравномерность в пределах полосы пропускания. Дадим определения этих параметров.

Полосой пропускания в общем случае называется заданный диапазон частот 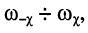характеризующий избирательность.

Шириной полосы пропускания 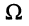(или F ) называется разность между заданными верхней 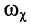и нижней 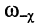частотами полосы            пропускания

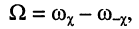     (13.14)

или

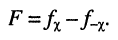     (13.15)

Идеальная АЧХ должна быть прямоугольной формы (рис. 13.2), а именно: быть равной "1" в пределах полосы пропускания и равной "0" вне её пределов:

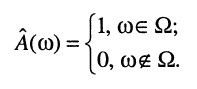
Однако АЧХ реальных контуров отличается от идеальной некоторым отклонением, которое всегда задаётся константой, характеризующей степень этого отклонения.

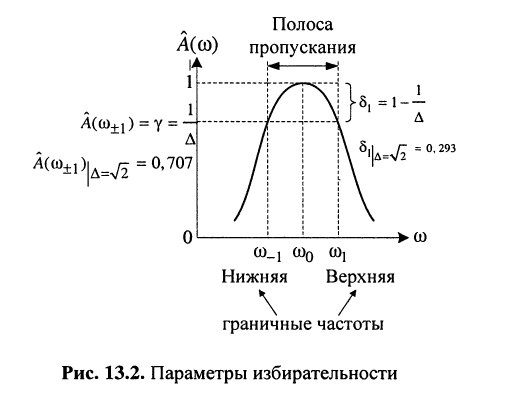
Неравномерностью называют максимально допустимую величину отклонения АЧХ от идеальной 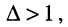 в связи с которой вводится другое, основное определение полосы пропускания.

Полосой пропускания контура называют полосу частот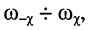 в пределах которой неравномерность его АЧХ не превышает заданного значения  Верхняя и нижняя частоты полосы пропускания также называются частотами среза.

Приведённое определение означает, что значения АЧХ на нижней и верхней частотах среза составляют

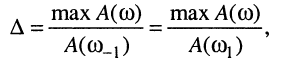      (13.16)

где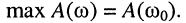 

Из определения (13.16) следует, что неравномерность равна обратному значению нормированной АЧХ на частотах среза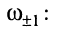

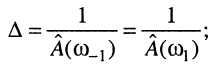       (13.17)

с другой стороны, значение нормированной АЧХ на этих частотах обратно неравномерности:

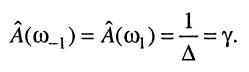      (13.18)

В задачах синтеза и анализа электрических цепей важной характеристикой является максимально допустимое отклонение ,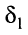
АЧХ 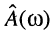от 1 в полосе пропускания

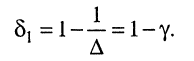      (13.19)

В технике радиосвязи полосу пропускания чаще всего определяют в пределах частот 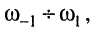 где АЧХ 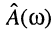составляет не менее чем 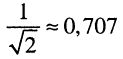, что соответствует неравномерности АЧХ  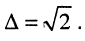Максимально допустимое отклонение в полосе пропускания при этом равно 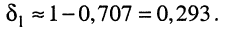Если перейти к логарифмическим АЧХ, получим в данном случае максимально допустимое ослабление в полосе пропускания, равное 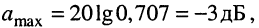а максимально допустимое затухание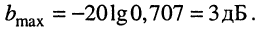

Связь полосы пропускания с вторичными параметрами

Избирательные свойства контура полностью зависят от его первичных параметров. Однако удобнее зависимость ширины полосы пропускания Q выразить через вторичные параметры, в свою очередь являющиеся функциями первичных параметров.

Для вывода связи полосы пропускания с вторичными параметрами воспользуемся выражениями (13.6) и (13.18):

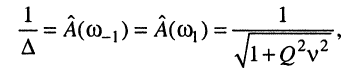
откуда имеем:

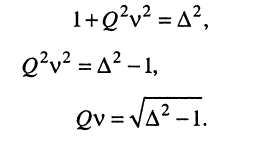     (13.20)

Подставим в последнее выражение формулу (13.4) относительной расстройки

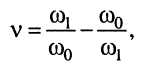
тогда получим:

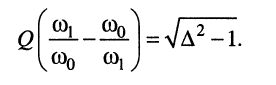
Выразим частоту со, в знаменателе второй дроби через частоты 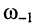 и 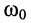согласно (13.8)

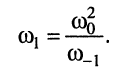
Тогда после очевидных преобразований

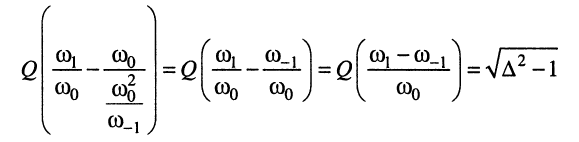
приходим к окончательным формулам:

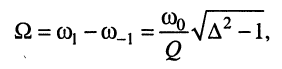    (13.21)
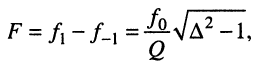       (13.22)

откуда следует, что полоса пропускания пропорциональна резонансной частоте и неравномерности и обратно пропорциональна добротности контура.

При неравномерности 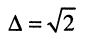ширина полосы пропускания определяется простой формулой:

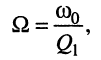         (13.23)

а фазочастотная характеристика на границах полосы пропускания равна:

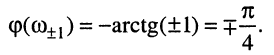        (13.24)

Следует обратить внимание на соответствие знаков "+" и "-" аргумента и результата. Действительно, из (13.20) имеем

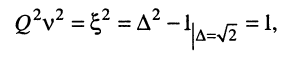
откуда аргумент равен

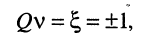
где "-1" соответствует частоте 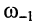, (расстройка отрицательная), а "+1" соответствует частоте 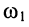, (расстройка положительная).

Выводы:

• чем больше добротность контура, тем уже его полоса пропускания;
• уменьшение неравномерности приводит к сужению полосы пропускания;
• увеличение резонансной частоты приводит к расширению полосы пропускания;
• значение ФЧХ на границах полосы пропускания является величиной постоянной и равной

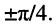
Управление шириной полосы пропускания параллельного колебательного контура с помощью шунта

Параллельный колебательный контур занимает центральное место в устройствах селекции сигналов по частоте, поэтому важным является обеспечение требуемой ширины полосы пропускания для сигналов с различными частотными свойствами. Это можно осуществлять с помощью изменения добротности контура. В свою очередь, добротностью контура можно управлять с помощью переменного шунта 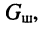подключаемого параллельно контуру (рис. 13.3).

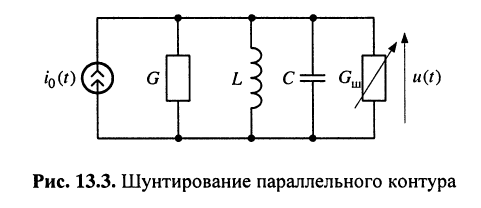
Найдём формулу для расчёта сопротивления 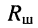шунта, обеспечивающего

расширение полосы пропускания в N раз при неравномерности АЧХ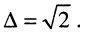

Пусть 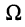 — ширина полосы пропускания контура до подключения шунта, и добротность контура 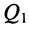равнялась

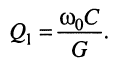
Тогда согласно (13.23) ширина полосы пропускания

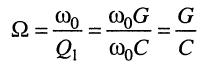           (13.25)

и при увеличении её в N раз имеем

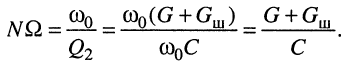       (13.26)

Поделив (13.25) на (13.26), получаем

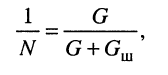     (13.25)

откуда

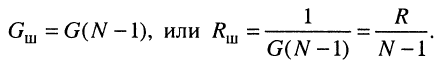      (13.27)

Следствия:

• Добротность контура тем выше, а ширина полосы пропускания тем меньше, чем больше сопротивление шунта.
• Добротность контура максимальна, а ширина полосы пропускания минимальна, если сопротивление шунта (его проводимость)          

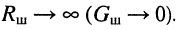
Частотные характеристики сложных колебательных контуров

В лекциях 11 и 12 были подробно рассмотрены АЧХ и ФЧХ последовательных и параллельных контуров. И те, и другие контуры находят широкое применение в устройствах телекоммуникации для селекции (фильтрации) разнообразных сигналов по частоте. Оказывается, что рассмотренные частотные характеристики приближённо справедливы в окрестности резонансных частот и для других разновидностей колебательных контуров, исследованию которых посвящён разд. 14.1 данной лекции. Кроме того, в разнообразных усилительных каскадах с целью повышения качества селекции используются так называемые связанные контуры, которые изучаются в разд. 14.2.

Некоторые разновидности параллельных колебательных контуров

При анализе реальных колебательных контуров всегда следует учитывать потери в катушках индуктивности за счёт конечности сопротивления провода и в конденсаторах вследствие не идеальности диэлектрика. Учёт этих потерь (см. разд. 3.3) производится включением последовательно с индуктивностью активного сопротивления и параллельно конденсатору активной проводимости. Если потери малы, то для получения частотных характеристик таких контуров при некоторых условиях, устанавливаемых далее, можно с высокой степенью приближения пользоваться строгой формулой (12.14).

Параллельный контур с малыми потерями в катушке индуктивности

Задача 14.1.

Найти приближённое выражение для частотных характеристик колебательного контура со схемой замещения, изображённой на
рис. 14.1,  при условии 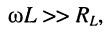оценить величину относительной погрешности 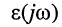частотных характеристик при их приближённом выражении.

Схема рис. 14.1 отличается от схемы замещения параллельного колебательного контура рис. 12.1 тем, что потери в катушке индуктивности учтены с помощью сопротивления 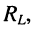включённого последовательно с индуктивностью. Такая схема хорошо отражает частотные свойства катушки индуктивности в области нижних частот (см. разд. 3.3).

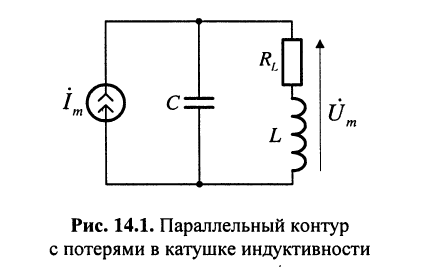
Решение. Комплексная частотная характеристика по напряжению для данного контура имеет вид:

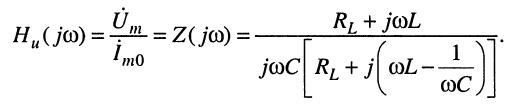          (14.1)

В полосе пропускания модуль реактивной составляющей сопротивления катушки индуктивности существенно превышает активную составляющую её сопротивления

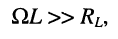
поэтому первым слагаемым числителя можно пренебречь. Тогда имеем: 

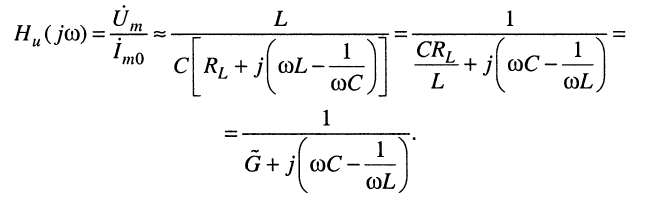        (4.12)

Комплексную относительную погрешность 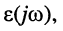обусловленную произведённым преобразованием в числителе, можно определить по формуле

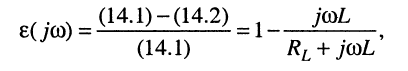       (14.1)    

откуда

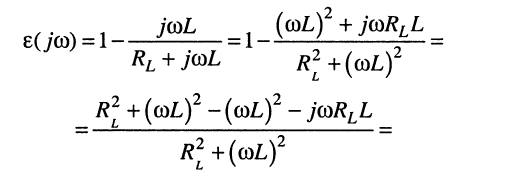  (14.3)
   

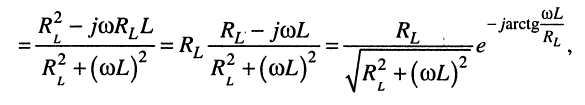
Где модуль

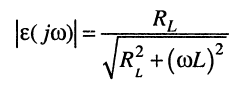       (14.4)

представляет собой относительную погрешность АЧХ, а аргумент — абсолютную погрешность ФЧХ, вычисляемых по приближённой формуле (14.2), которая не отличается от строгой формулы (12.14)

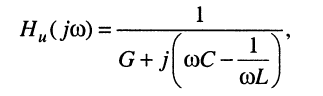
полученной для КЧХ параллельного колебательного контура с теми же значениями индуктивности L и ёмкости С, но имеющего активную проводимость

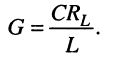                 (14.5)

Задача 14.2.

Найти приближённое выражение для частоты резонанса 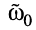контура (см. рис. 14.1).

Решение. Рассмотрим точное выражение для проводимости контура

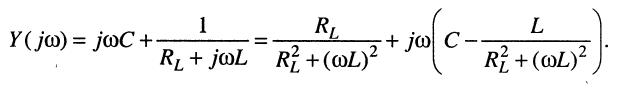
Мнимая часть проводимости на резонансной частоте 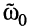должна быть равна нулю (см. лекцию 12)

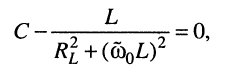
поэтому

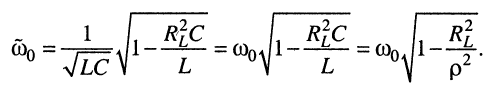
Понятно, что при

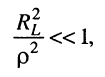
т. е. когда волновое сопротивление 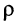во много раз превышает потери 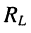в катушке индуктивности

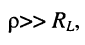
что нередко имеет место на практике, резонансная частота рассматриваемого контура очень близка к резонансной частоте параллельного контура, изображённого на рис. 12.1:

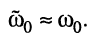
Следствия:

Рассмотренный колебательный контур приближённо эквивалентен параллельному колебательному контуру, имеющему:

вторичные параметры:

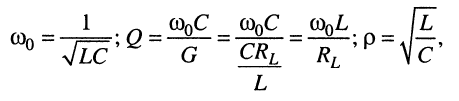
полосу пропускания

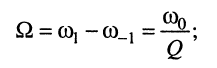        (14.6)

резонансное сопротивление

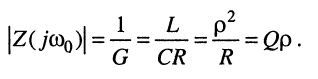         (14.7)

При высокой добротности контура относительная погрешность приближения АЧХ (14.4) оказывается весьма малой; так, для частот 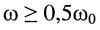при добротности Q = 200 относительная погрешность АЧХ не превышает 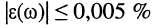и уменьшается с ростом частоты.

Параллельный контур с малыми потерями в катушке индуктивности и конденсаторе

Рассмотрим другой контур (рис. 14.2), имеющий дополнительную активную проводимость 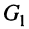, моделирующую потери в конденсаторе. Эта проводимость добавляется к (14.5) и потому общая проводимость контура равна:

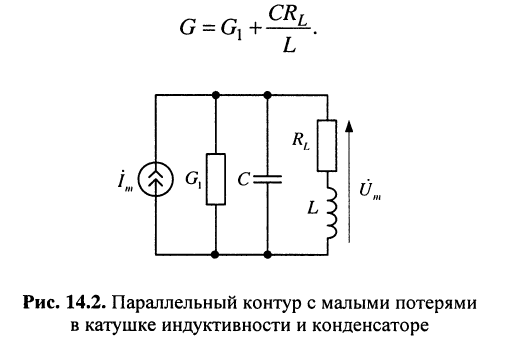
Полагая, как и в разд. 14.1.1, что в полосе пропускания контура 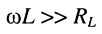и, кроме того, 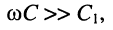что справедливо для используемых в радиотехнике контуров, рассматриваемый контур имеет:

вторичные параметры:

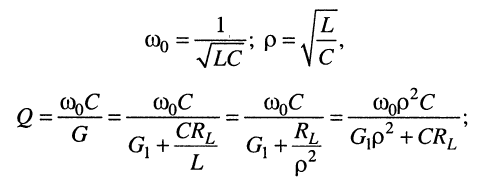
полосу пропускания

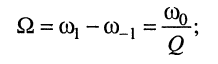
резонансное сопротивление

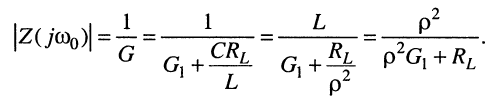
Погрешность при сделанных допущениях оценивается тем же способом, что и в разд. 14.1.1.

Связанные колебательные контуры

Во входных цепях радиоприёмников, в усилителях различного назначения, в выходных каскадах радиопередатчиков, в фильтрах сосредоточенной селекции требуется получить очень высокую избирательность АЧХ. На одиночных колебательных контурах этого добиться невозможно, поэтому применяются связанные контуры.

Определение:

Связанными контурами называются избирательные цепи, состоящие из двух, чаще всего одинаковых, колебательных контуров, между которыми существует реактивная связь такая, что возбуждение электрических колебаний в одном из них приводит к возникновению колебаний в другом.

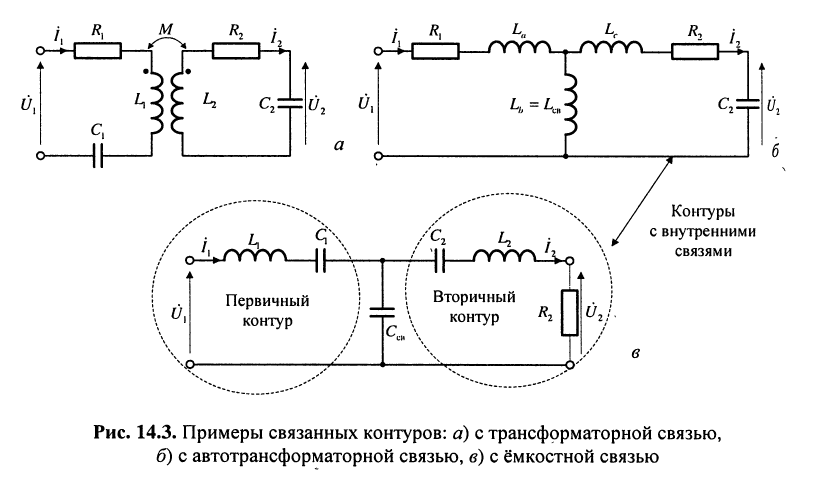
В зависимости от вида связи различают контуры:

• с трансформаторной связью (рис. 14.3, а),
• с автотрансформаторной связью (рис. 14.3, б),
• с ёмкостной связью (рис. 14.3, в).

Автотрансформаторную и ёмкостную связь называют внутренней. Контур, на который подаётся внешнее воздействие 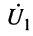, будем называть первичным. Контур, ток 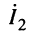или напряжение 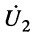которого рассматриваются как реакция на внешнее воздействие, будем называть вторичным.

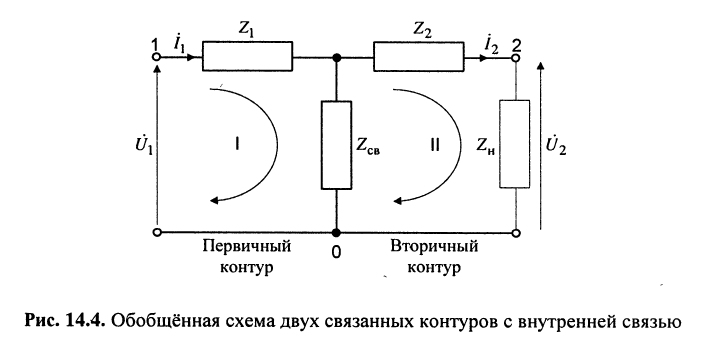
Коэффициент связи

Рассмотрим обобщённую схему двух связанных контуров (рис. 14.4), в которой комплексные сопротивления Z, содержат активные и реактивные составляющие. Важной характеристикой связанных контуров является коэффициент связи, определяемый с помощью формулы

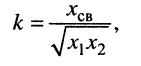    (14.8)

где

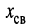— реактивная составляющая комплексного сопротивления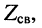

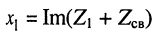и 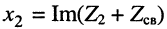— реактивные составляющие сопротивлений первичного и вторичного контуров того же знака, что и 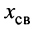(см. рис. 14.4).

Из определения (14.8) получаем:

для контура с трансформаторной связью (см. лекцию 9)

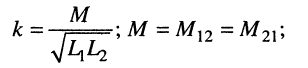      (14.9)

для контура с автотрансформаторной связью

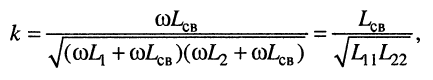      (14.10)

где

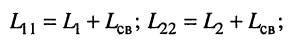
для контура с ёмкостной связью

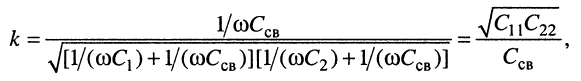
где 

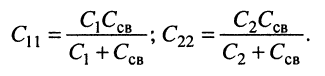
Следствия:

• Коэффициент связи является количественной оценкой степени связи между контурами и не зависит от частоты.
• Значение коэффициента связи не может превышать единицы.

Комплексные амплитуды токов связанных контуров

Для обобщённой схемы двух связанных контуров (рис. 14.4) нетрудно записать систему уравнений

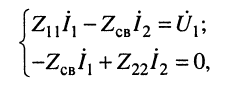    (14.12)

где 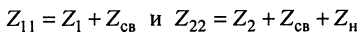являются собственными сопротивлениями первичного и нагруженного вторичного контуров соответственно.

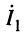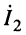Решая систему (14.12) относительно токов и , получаем:

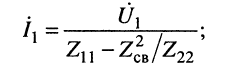      (14.13)

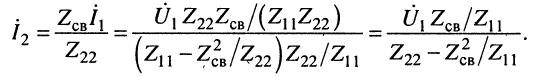       (14.14)

Исследуем выражения (14.13) и (14.14). Знаменатель (14.13) имеет смысл входного сопротивления связанных контуров со стороны зажимов 0-1, но это сопротивление отличается от собственного сопротивления первичного контура на величину 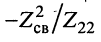; эта величина отражает влияние вторичного контура на первичный контур. Аналогично в (14.14) величина , 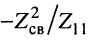отражает влияние первичного контура на вторичный контур. Эти величины называются вносимыми сопротивлениями.

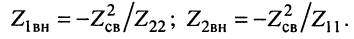       (14.15)

Подставляя (14.15) в (14.13) и (14.14), получаем:

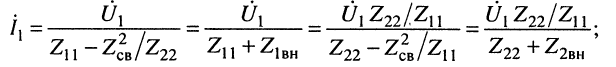          (4.16)

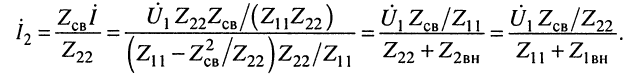       (4.17)

Полученные выражения позволяют исследовать частотные свойства связанных контуров. Наиболее важным является режим резонанса, которого добиваются путём настройки связанных контуров.

Настройки связанных контуров

Настройка связанных контуров состоит в таком подборе параметров реактивных элементов контуров, при котором достигается требуемый резонанс в системе связанных контуров. Для удобства анализа частотных характеристик связанных контуров в соответствии с (14.16) и (14.17) построим пары одноконтурных схем замещения рис. 14.5, а, б и рис. 14.5, в, г.

Различают четыре вида настроек:

1. Первый частный резонанс обеспечивает максимум тока в первом контуре (рис. 14.5, а)

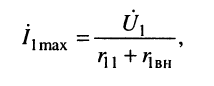       (14.18)

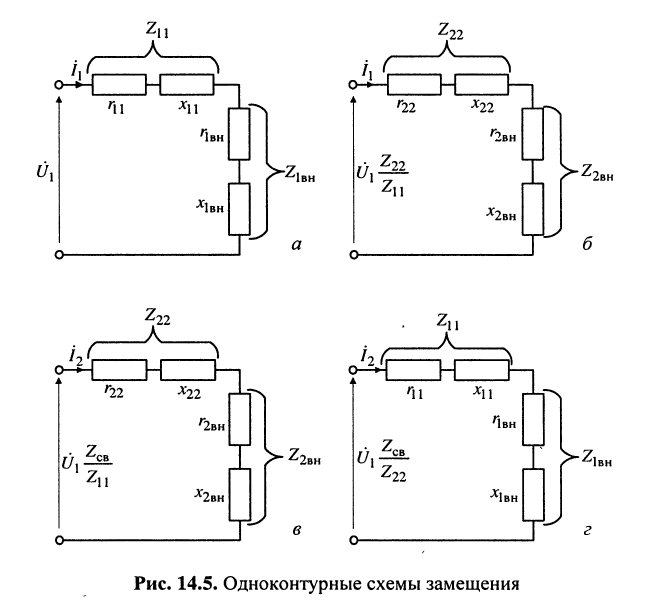
что достигается настройкой до выполнения условия (см. лекцию 13)

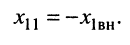
2. Второй частный резонанс обеспечивает максимум тока во втором контуре (рис. 14.5, в)

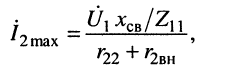      (4.19)

что достигается настройкой до выполнения условия

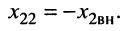
3. Сложный резонанс выполняется в два этапа и состоит в том, что один из контуров настраивается на частный резонанс, а затем подбирается оптимальное сопротивление связи

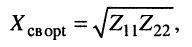            (14.20)

при котором ток 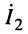во вторичном контуре достигает максимально возможного значения (максимум максимомум)

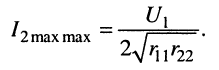       (14.21)

Можно показать, что максимально возможное значение тока во вторичном контуре при настройке на сложный резонанс не зависит от того, какой из контуров предварительно был настроен на частный резонанс. Действительно, настройка в первый частный резонанс и подбор связи (14.20) эквивалентен условию

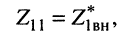     (14.22)

а настройка во второй частный резонанс и подбор связи (14.20) эквивалентен условию

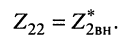      (14.23)

4. Полный резонанс имеет наибольший практический интерес. Настройка, как и в случае сложного резонанса, осуществляется в два этапа: сначала каждый из связанных контуров настраивается на индивидуальный резонанс (см. лекцию 13), когда 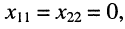а затем подбирается оптимальное сопротивление связи

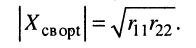    (14.24)

При этом ток 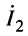определяется формулой (14.21).

Частотная зависимость тока во вторичном контуре

Связанные контуры, применяемые во входных цепях радиоприёмников и в фильтрах сосредоточенной селекции, используются в режиме передачи максимальной мощности во вторичный контур, т. е. при

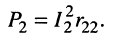
По этой причине из всех частотных характеристик наибольший интерес представляет частотная зависимость тока 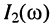во вторичном контуре, которую и найдём из "формулы (14.17). Предварительно выразим собственные сопротивления первичного 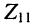и вторичного 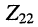контуров (рис. 14.4) через обобщённые расстройки (13.5) связанных контуров: 

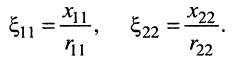
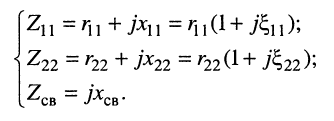        (14.25)

Здесь принято, что комплексное сопротивление связи имеет чисто реактивный характер. Подставив (14.25) в (14.17) и учтя соотношение 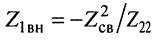, получаем выражение для комплексной амплитуды тока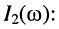

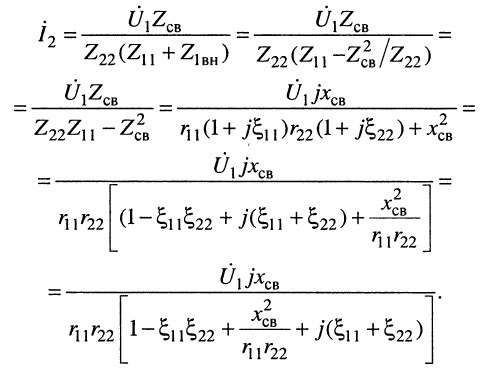            (14.26)

Рассмотрим дробь, принадлежащую вещественной части знаменателя. Заменим в (14.26) 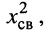, для чего воспользуемся формулой (14.8) коэффициента связи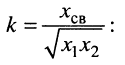

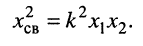
Тогда получим:

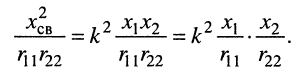
С другой стороны, на частотах, близких к частоте резонанса, можно считать, что реактивные сопротивления 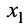и 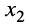приближённо равны волновым сопротивлениям контуров (11.18):

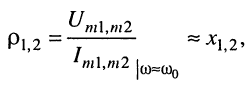
поэтому по определению добротности (11.29) имеем:

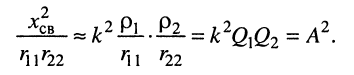
Величина

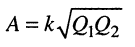
называется фактором связи. Подставим (14.28) в (14.26)

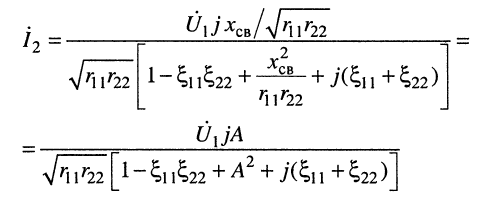
и без потери общности при 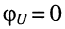запишем выражение для амплитуды тока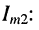

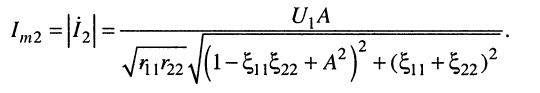      (14.29)

Разделим (14.29) на максимально возможное значение тока 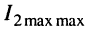что даст нормированную функцию

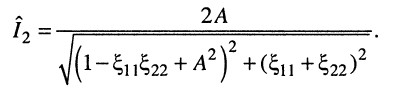         (14.30)

Ранее уже отмечалось, что типовым случаем для связанных контуров является их идентичность. В этом случае их добротности и обобщённые расстройки оказываются равными:

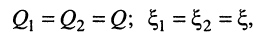
а выражение (14.30) принимает вид:

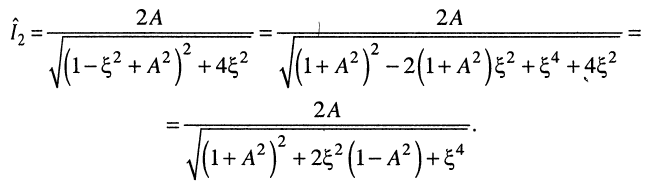         (14.31)

Понятно, что поскольку обобщённая расстройка является функцией частоты, то и амплитуда тока (14.29) и безразмерная нормированная характеристика (14.31) также частотно зависимы и полностью выражают частотные свойства связанных контуров.

Частотные свойства связанных контуров

Из выражения (14.31) следует, что вид нормированной характеристики 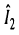полностью определяется значением фактора связи, который при идентичности контуров равен:

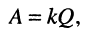
а выражение (14.31), подлежащее анализу, приводится к виду

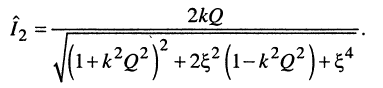      (14.33)

Коэффициент связи, как было установлено в разд. 14.2.1, не может превышать единицы 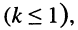поэтому все свойства 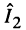определяются фактором связи, в зависимости от значения которого можно выделить три вида связи:

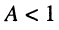•     — слабая связь,
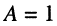•     — критическая связь,
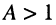•     — сильная связь.

Поскольку регулировка связи осуществляется за счёт изменения сопротивления связи (см. рис. 14.4), желательно вид связи выразить непосредственно через коэффициент связи, что можно сделать, если воспользоваться вторичным параметром — затуханием контура (11.30)

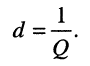
Тогда с учётом фактора связи

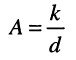
получаем, что:

• слабой связи соответствует
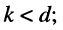
• критической связи соответствует
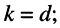
• сильной связи соответствует

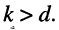
С целью выявления частотных свойств 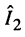исследуем функцию (14.33) на расположение её экстремумов, для чего возьмём производную от неё по переменной 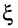и числитель приравняем нулю:

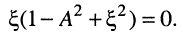
Это уравнение имеет три корня:

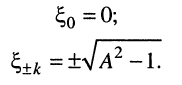
Для удобства выразим корни через приближённое выражение для относительной расстройки (13.4):

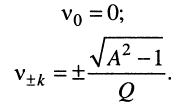
Слабая связь:

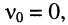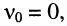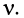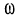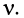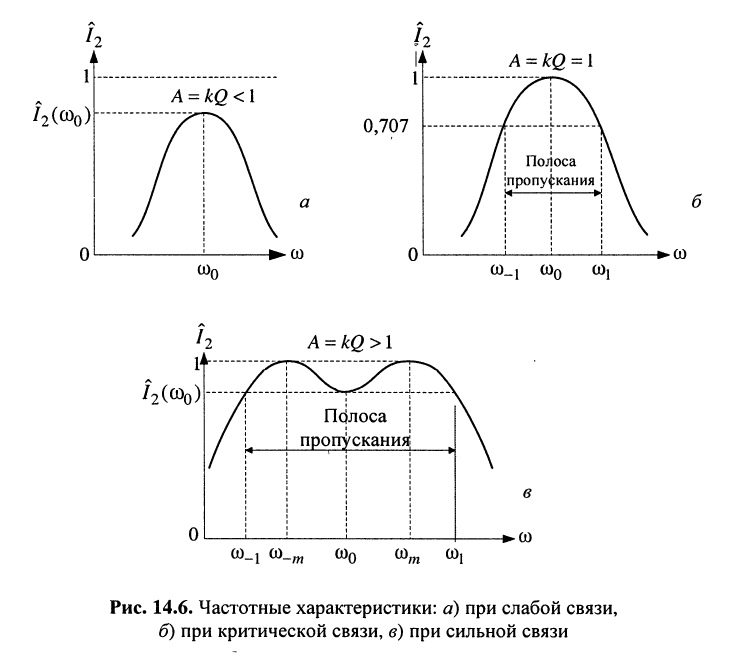
При слабой связи функция (14.34) имеет один экстремум при , т. е. на частоте и два других экстремума при мнимых значениях относительной расстройки Однако вещественным и положительным значениям частоты соответствуют лишь вещественные значения расстройки Поэтому функция (14.34) имеет единственный экстремум на частоте 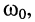и этот экстремум может быть только максимумом (рис. 14.6, а).

Значение максимума найдём из (14.33) при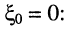

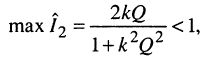      (14.35)

т. е. при слабой связи максимум характеристики 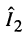не может превосходить единицы.

Критическая связь:

При критической связи 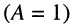все три экстремума функции (14.34) располагаются на частоте 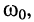поскольку 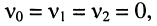а максимум (рис. 14.6, б) равен единице:

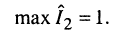
Характеристика при критической связи называется максимально плоской.

Сильная связь:

При сильной связи функция (14.34) имеет три вещественных экстремума при относительных расстройках 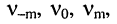которым соответствуют частоты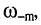 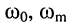(рис. 14.6, в).

Получим значения этих частот, используя приближённое выражение для относительной расстройки (13.11):

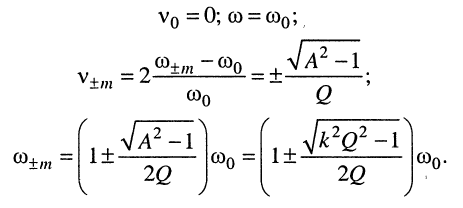             (14.36) 

Значения 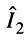на соответствующих частотах при сильной связи таковы:

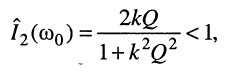
т. е. такое же, как на резонансной частоте в случае слабой связи; при подстановке в (14.33) обобщённой расстройки (14.34) после замены индекс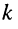а на 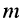получаем

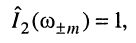
что и отображено на рис. 14.6, в.

Следствия:

• На частотах 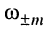располагаются равные по величине максимальные значения тока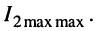
• На резонансной частоте 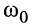имеет место провал частотной характеристики 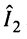, соответствующий её минимуму; глубина провала будет тем больше (минимум тем меньше), чем больше фактор связи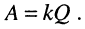

Полоса пропускания связанных контуров

На практике связанные контуры со слабой связью не используются, поэтому рассмотрим полосы пропускания в случаях критической и сильной связи.

Критическая связь:

В данном случае, как указывалось ранее, получаем максимально плоскую частотную характеристику, причём 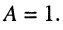 По этой причине связанные контуры можно рассматривать как одиночный контур, полосу пропускания которого определяют как ту область частот 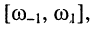где значения частотной характеристики составляют не менее чем 0,707 от её максимального значения.

Это означает, что при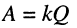

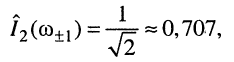
или

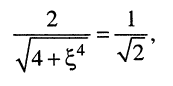
откуда

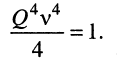
Последнее уравнение имеет два вещественных корня:

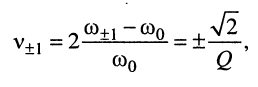
поэтому граничные частоты (рис. 14.6, б)

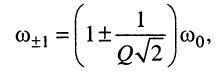
а ширина полосы пропускания равна

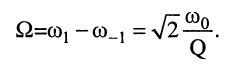
Следовательно, как и для одиночных контуров, ширина полосы пропускания связанных контуров при критической связи прямо пропорциональна резонансной частоте и обратно пропорциональна добротности.

Сильная связь:

При сильной связи частотная характеристика становится двугорбой, поэтому для сильной связи принято иное определение полосы пропускания.

Определение:

Полосой пропускания связанных контуров в случае сильной связи называют полосу частот, в пределах которой АЧХ принимает значения, не меньшие, чем её минимальное значение на резонансной частоте (рис. 14.6, в).

Согласно этому определению необходимо, чтобы соблюдалось равенство:

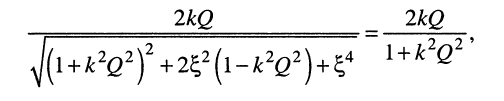
откуда при 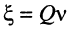  нетрудно получить четыре корня:

• двукратный корень
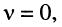
• два вещественных корня, соответствующих граничным частотам:

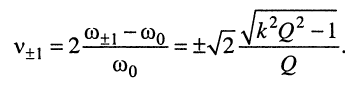
Следовательно, граничные частоты определятся по формуле

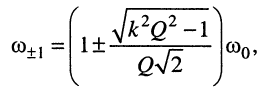
а ширина полосы пропускания — по формуле

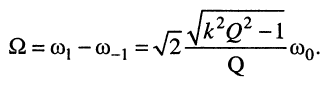
полученные соотношения позволяют сделать следующие выводы:

• амплитудно-частотные характеристики связанных контуров за пределами полосы пропускания убывают значительно быстрее,          чем у одиночного контура;
• связанные контуры обеспечивают более сильное, чем одиночный контур, подавление всех гармонических составляющих                        воздействия (например, помех), частоты которых лежат за пределами полосы пропускания;
• сильная связь позволяет получить наибольшую крутизну спада АЧХ вне полосы пропускания за счёт увеличения                                      неравномерности в полосе пропускания, что не всегда является допустимым.