
Функция одной переменной - определение и вычисление с примерами решения
Содержание:
Понятие функции:
При изучении тех или иных процессов действительного мира мы встречаемся с характеризующими их величинами, меняющимися в течение изучения этих процессов. Причем всегда имеется несколько переменных величин, одни из которых могут изменяться произвольно, а другие уже в зависимости от изменения первых. Тогда говорят, что между этими переменными существует функциональная зависимость. Говоря точнее, числовая последовательность 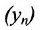
Определение 10.1.1. Пусть заданы два множества X и У. Если каждому элементу 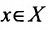 поставлен в соответствие по известному закону один и только один элемент
поставлен в соответствие по известному закону один и только один элемент 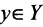 , обозначаемый
, обозначаемый 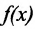 и если элемент
и если элемент 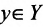 при этом оказывается поставленным в соответствие хотя бы одному элементу
при этом оказывается поставленным в соответствие хотя бы одному элементу 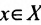 , то говорят, что на множестве X задана однозначная функция
, то говорят, что на множестве X задана однозначная функция 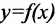 . Множество X называется её областью определения, а Y- множество значений. Элемент х называется аргументом или независимой переменной, а у- значением функции, или зависимой переменной.
. Множество X называется её областью определения, а Y- множество значений. Элемент х называется аргументом или независимой переменной, а у- значением функции, или зависимой переменной.
Из определения следует, что для задания функции /, надо задать:
- её область определения - множество X;
- её область значений - множество У;
- закон соответствия, по которому определяется элемент
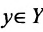 , соответствующий элементу
, соответствующий элементу 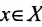 , т.е. элементy
, т.е. элементy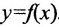 .
.
Подчеркнем, что понятие функции равносильно понятию соответствия: например, не функция sinx, а функция sin. Заметим, что элементы х и у множеств X и Y могут иметь различную природу; т.е. являться вещественными либо комплексными числами. Если функции 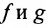 рассматриваются на множестве X, то запись
рассматриваются на множестве X, то запись 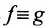 означает, что
означает, что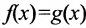 , для любых
, для любых 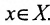 . Числовая функция (функция, принимающая числовые значения) называется ограниченной снизу (сверху), если множество её значений ограничено снизу (сверху). Функция, ограниченная на множестве X как сверху, так и снизу, называется ограниченной.
. Числовая функция (функция, принимающая числовые значения) называется ограниченной снизу (сверху), если множество её значений ограничено снизу (сверху). Функция, ограниченная на множестве X как сверху, так и снизу, называется ограниченной.
Верхняя (нижняя) грань множества значений Y числовой функции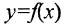 определенной на множестве X, называется верхней (нижней) гранью функции/ и обозначается:
определенной на множестве X, называется верхней (нижней) гранью функции/ и обозначается: 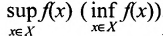 . Иногда приходится иметь дело с функциями
. Иногда приходится иметь дело с функциями 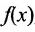 , определенными на некотором множестве X, значениями которых являются некоторые подмножества Y, т.е. каждому элементу
, определенными на некотором множестве X, значениями которых являются некоторые подмножества Y, т.е. каждому элементу 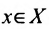 ставится в соответствие некоторое множество
ставится в соответствие некоторое множество 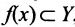 , и, тем самым множеством значений функции является совокупность некоторых подмножеств множества Y Если каждая
, и, тем самым множеством значений функции является совокупность некоторых подмножеств множества Y Если каждая 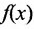 состоит только из одного элемента
состоит только из одного элемента 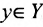 , то получится однозначная функция, в противном случае, получаем многозначную функцию.
, то получится однозначная функция, в противном случае, получаем многозначную функцию.
В дальнейшем будем изучать однозначные функции. Рассмотрим способы задания таких функций. Они могут быть заданы следующими способами:
1. Функции могут задаваться при помощи одной или нескольких формул. Например.
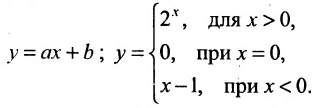
Такой способ задания называется аналитическим способом. Существуют специальные способы аналитического задания функции:
- - неявные функции, т.е. функции вида
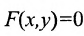 , в которых у не разрешено относительно х
, в которых у не разрешено относительно х - - сложные функции. Например, функция
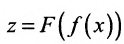 является суперпозицией двух функций
является суперпозицией двух функций 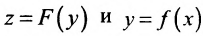 • Область определения функции F является множеством значений функции
• Область определения функции F является множеством значений функции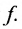 Каждому значению х из области определения функции
Каждому значению х из области определения функции 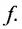 естественным образом соответствует z, такое, что
естественным образом соответствует z, такое, что 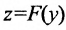 , где
, где 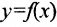 . Можно рассматривать суперпозицию и большего числа функций. Например,
. Можно рассматривать суперпозицию и большего числа функций. Например,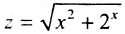 .
.
2. Функция может быть указана описанием соответствия, по которому независимой переменной х соответствует зависимая переменная у. Например: каждому рациональному числу поставим в соответствие число 1, а каждому иррациональному - число нуль. Получим функцию Дирихле:
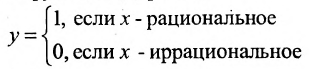
3. Функция может быть задана графически.
Определение 10.1.2. Графиком функции 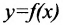 называется геометрическое место точек на плоскости с координатами
называется геометрическое место точек на плоскости с координатами 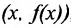
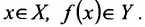
4. Функцию можно задать с помощью таблицы, в которой для некоторых значений х указываются соответствующие значения у. Для нахождения значений функции тех значений аргумента которых нет в таблице применяется интерполирование.
Введем еще одно важное определение.
Определение 10.1.3. Простейшими элементарными функциями называются следующие функции: 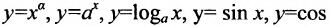
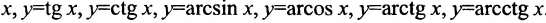
Определение 10.1.4. Всякая функция, которая может быть задана с помощью формулы, содержащей лишь конечное число арифметических операций и суперпозиций основных элементарных функций, называется просто элементарной функцией.
Элементарные функции делятся на классы:
Многочлены (полиномы):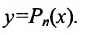
Рациональные функции:
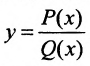
где Р(х), Q(x) - многочлены.
Алгебраические функции: например, 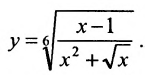
Трансцендентные функции: например, 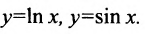
Пределы функций
Пусть функция определена на некотором множестве X, и пусть 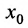 - точка бесконечной прямой
- точка бесконечной прямой 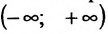 быть может и не принадлежащая этому множеству X, но обладающая тем свойством, что в любой
быть может и не принадлежащая этому множеству X, но обладающая тем свойством, что в любой 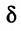 - окрестности
- окрестности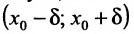 этой точки
этой точки 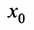 имеются точки множества X, отличные от
имеются точки множества X, отличные от 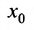 . Это означает, что
. Это означает, что 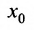 - предельная точка множества X. При любом
- предельная точка множества X. При любом 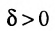 интервал
интервал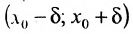 из которого исключена точка х0, называют проколотой окрестностью точки
из которого исключена точка х0, называют проколотой окрестностью точки 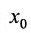 .
.
Определение 10.2.1. (по Коши) Пусть функция f определена на интервале (а,Ь), кроме быть может точки 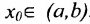 . Число А называется пределом функции f в точке
. Число А называется пределом функции f в точке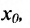 , если для любого
, если для любого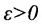 существует такое число
существует такое число 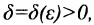 , что для всех
, что для всех 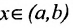 и удовлетворяющих условию
и удовлетворяющих условию 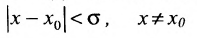 выполняется неравенство
выполняется неравенство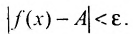
Если такое число А существует, то пишут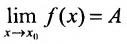 .
.
Для односторонних пределов функции в точке можно также сформулировать следующее определение.
Определение 10.2.2. Пусть функция f определена на полуинтервале 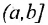 (соответственно на [а,b) ). Число В называется пределом функции слева (справа) в точке
(соответственно на [а,b) ). Число В называется пределом функции слева (справа) в точке 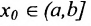 (соответственно в точке
(соответственно в точке 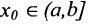 , если для любого
, если для любого 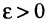 существует
существует 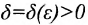 такое,. что
такое,. что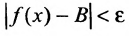 для всех х, удовлетворяющих условию
для всех х, удовлетворяющих условию
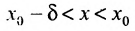 (соответственно
(соответственно 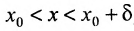 )
)
Если такое число В существует, то пишут 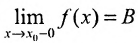 (соответствснно
(соответствснно 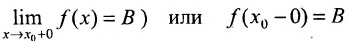 (соответственно
(соответственно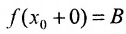 ). Определения пределов функции и односторонних пределов функции эквивалентны. Связь же между односторонними пределами и двусторонним пределом устанавливается следующей теоремой. •
). Определения пределов функции и односторонних пределов функции эквивалентны. Связь же между односторонними пределами и двусторонним пределом устанавливается следующей теоремой. •
Теорема 10.2.1. Функция f имеет предел в точке тогда и только тогда, когда в этой точке существуют пределы, как справа. так и слева и они равны. Тогда их общее значение и является пределом функции f в точке 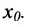 .
.
Доказательство. Необходимость. Пусть 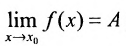 ; покажем, что односторонние пределы равны. Так как функция f имеет предел в некоторой точке то для любого
; покажем, что односторонние пределы равны. Так как функция f имеет предел в некоторой точке то для любого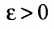 существует такое
существует такое 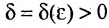 , что из неравенства
, что из неравенства 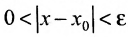 , т.е. из неравенства
, т.е. из неравенства 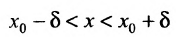 следует неравенство
следует неравенство 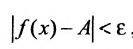 но тем более
но тем более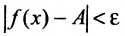 будет для всех x, удовлетворяющих условиям
будет для всех x, удовлетворяющих условиям 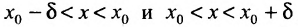 , так как объединение этих полуинтервалов является интервал
, так как объединение этих полуинтервалов является интервал 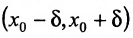 , что и означает существование односторонних пределов, равных пределу А:
, что и означает существование односторонних пределов, равных пределу А: 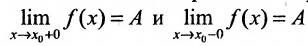
Достаточность. Обратно, пусть существуют в этой точке односторонние пределы, и они равны: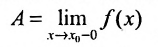 и.
и.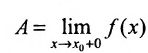 Покажем, что функция f имеет предел в этой точке равный этим односторонним пределам. Действительно, так как существуют односторонние пределы, то для заданного
Покажем, что функция f имеет предел в этой точке равный этим односторонним пределам. Действительно, так как существуют односторонние пределы, то для заданного 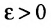 существуют такие числа
существуют такие числа 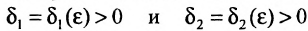 , что если
, что если 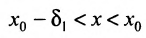 и соответственно
и соответственно 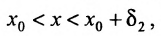 то
то 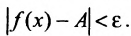 . Положив
. Положив 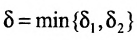 , тем более получим, что
, тем более получим, что 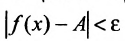 при
при 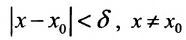 . А это и означает, что функция f имеет предел в точке
. А это и означает, что функция f имеет предел в точке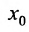 равный A:
равный A: 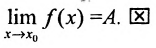
Арифметические операции над функциями, имеющими предел в точке
Справедлива следующая фундаментальная теорема, позволяющая вычислять пределы различных функций.
Теорема 10.3.1. Пусть две функции f и g заданы на одном и том же множестве X и имеют в точке 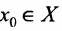 пределы, соответственно равные А и В. Тогда функции f ±g,
пределы, соответственно равные А и В. Тогда функции f ±g, 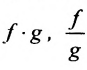 ,— имеют в точке
,— имеют в точке 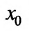 пределы, соответственно равные А±В,
пределы, соответственно равные А±В, 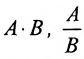 — (в случае частного нужно дополнительно требовать, чтобы
— (в случае частного нужно дополнительно требовать, чтобы 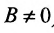 ).
).
Доказательство. Пусть функции f и g заданы на множестве X и имеют в точке 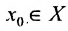 пределы соответственно равные А и В. Согласно определению 10.2.1 для любого
пределы соответственно равные А и В. Согласно определению 10.2.1 для любого 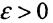 существуют такие числа
существуют такие числа 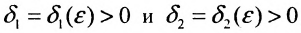 , что для всех
, что для всех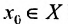 и удовлетворяющих условиям
и удовлетворяющих условиям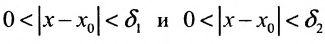 выполняются соответственно неравенства
выполняются соответственно неравенства 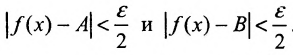 .
.
Рассмотрим функцию /±g, которая определена на множестве X и докажем, что она имеет предел в точке 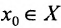 . Для заданного
. Для заданного 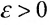 выберем такое число
выберем такое число 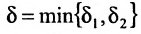 , что для всех
, что для всех 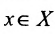 , удовлетворяющих условию.
, удовлетворяющих условию. 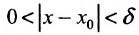 , оценим разность
, оценим разность 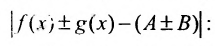
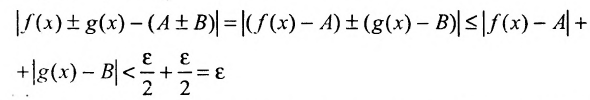
Таким образом, получим, что для заданного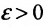 существует такое число
существует такое число 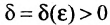 , что для всех
, что для всех 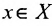 , удовлетворяющих условию
, удовлетворяющих условию 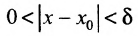 выполняется неравенство
выполняется неравенство 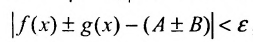 а это означает, что функция f ±g имеет предел в точке Хо равный А±В. .
а это означает, что функция f ±g имеет предел в точке Хо равный А±В. .
Аналогично доказываются и другие утверждения. 
Функция 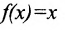 в любой точке
в любой точке 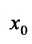 бесконечной прямой имеет предел, равный
бесконечной прямой имеет предел, равный 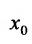 . Тогда, используя теорему 10.3.1, можно утверждать, что
. Тогда, используя теорему 10.3.1, можно утверждать, что
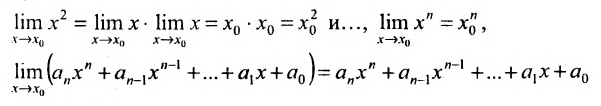
для любой точки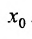 .
.
Сформулируем несколько свойств пределов функций, предполагая при этом, что они определены на некотором интервале (а,b) кроме, быть может точки 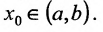 .
.
Свойство 10.3.1. Пусть функции 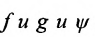 определены в некоторой окрестности точки
определены в некоторой окрестности точки 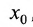 , за исключением быть может точки
, за исключением быть может точки
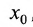 , и при всех х из этой окрестности выполняется неравенство
, и при всех х из этой окрестности выполняется неравенство 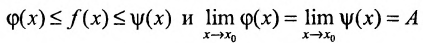 . Тогда
. Тогда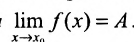 .
.
Свойство 10.3.2.. Если 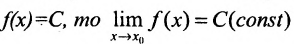 .
.
Свойство 10.3.3. Если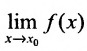 существует, то для любого числа С, С = const,
существует, то для любого числа С, С = const,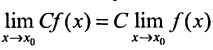 .
.
Рассмотрим пример применения теоремы 10.3.1.
Пример:
Вычислить предел функции 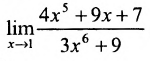 .
.
Решение:
Воспользуемся теоремой 10.3.1. Получим:
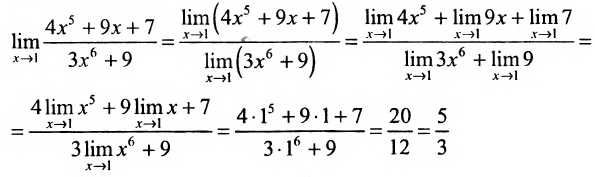
Два замечательных предела функций
Вычислим пределы конкретных функций.
Лемма 10.4.1. Предел функции 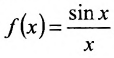 при
при 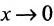 , соотвествует и равен I, т.е.
, соотвествует и равен I, т.е. 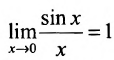 .
.
Доказательство. Рассмотрим круг радиуса R с центром в точке О. Пусть OA неподвижный радиус; ОВ - подвижный, образующий угол x. с радиусом OA. Выполним построения, указанные на рис. 10.1.
с радиусом OA. Выполним построения, указанные на рис. 10.1.
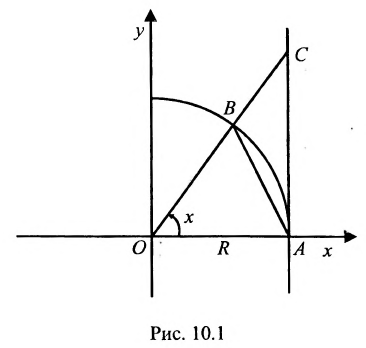
Тогда площадь 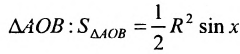 площадь сектора
площадь сектора 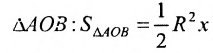 ; площадь
; площадь 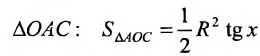 . Треугольник АОВ является частью сектора АОВ, который является частью
. Треугольник АОВ является частью сектора АОВ, который является частью 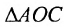 , поэтому
, поэтому 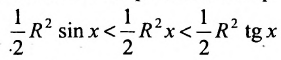 . Разделив все члены неравенства на
. Разделив все члены неравенства на 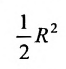 получим: sin х
получим: sin х 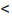 х
х 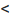 tg х, или
tg х, или 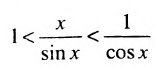 , или
, или 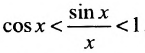 .
.
Так как 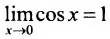 , то в силу свойства 2.2.1 из последнего не- равенства получим предел функции
, то в силу свойства 2.2.1 из последнего не- равенства получим предел функции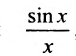 ,равный 1,т.е.
,равный 1,т.е.
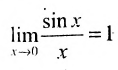 Лемма доказана.
Лемма доказана.
Лемма 10.4.2. Предел функции 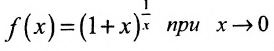 существует и равен е, т.е.
существует и равен е, т.е.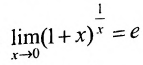
Следствие 10.4.1. 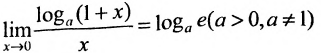 или при
или при 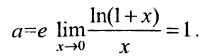
Действительно,
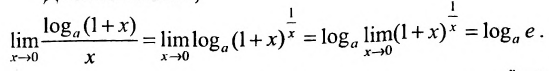
Следствие 10.4.2.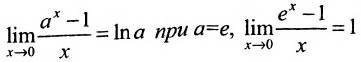
Доказательство.
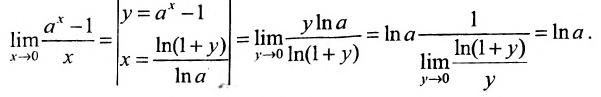 Следствие 10.4.5.
Следствие 10.4.5. 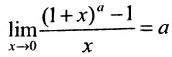
Бесконечно малые и бесконечно большие функции
Функция 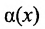 называется бесконечно малой в точке
называется бесконечно малой в точке 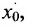 , если предел этой функции в точке
, если предел этой функции в точке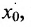 , равен нулю:
, равен нулю: 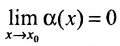 . Например, функция
. Например, функция 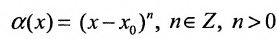 , является бесконечно малой в точке
, является бесконечно малой в точке 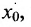 . Заметим, что если функция f имеет предел в точке
. Заметим, что если функция f имеет предел в точке  равный В, то функция
равный В, то функция 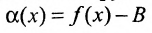 является бесконечно малой. Тогда, всякую функцию f, имеющую предел В в точке
является бесконечно малой. Тогда, всякую функцию f, имеющую предел В в точке 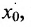 можно представить в виде
можно представить в виде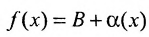 , где
, где 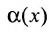 - бесконечно малая функция в точке
- бесконечно малая функция в точке 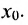
Функция у = А(х) называется бесконечно большой в точке 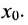 справа (слева), если
справа (слева), если 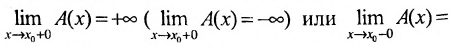
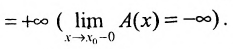
Остановимся на методике сравнения двух бесконечно малых в данной точке 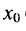 функций
функций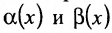 , предполагая, что они определены на одном множестве.
, предполагая, что они определены на одном множестве.
- Функция
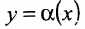 является бесконечно малой в точке х0 больше высокого порядка малости, чем
является бесконечно малой в точке х0 больше высокого порядка малости, чем 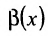 , если
, если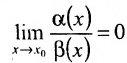
- Функции
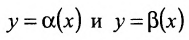 являются в точке
являются в точке 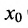 бесконечно малыми одного порядка, если
бесконечно малыми одного порядка, если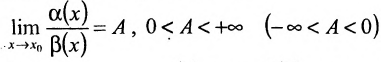
- Функции
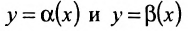 являются в точке
являются в точке 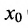 эквивалентными бесконечно малыми, если
эквивалентными бесконечно малыми, если 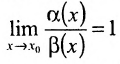 Функции
Функции 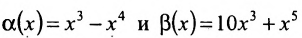 являются в точке х=4 эквивалентными бесконечно малыми, поскольку
являются в точке х=4 эквивалентными бесконечно малыми, поскольку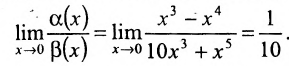 Функции
Функции 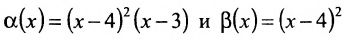 являются в точке х=0 бесконечно малыми одного порядка, так как
являются в точке х=0 бесконечно малыми одного порядка, так как 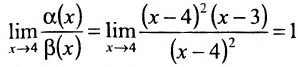 Аналогично сравниваются две бесконечно большие в данной точке
Аналогично сравниваются две бесконечно большие в данной точке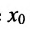 справа (или слева) функции
справа (или слева) функции 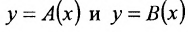 . Предположим, что функции
. Предположим, что функции 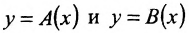 определены на одном множестве X и
определены на одном множестве X и 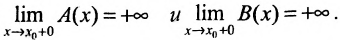 .
. - Функция
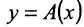 имеет в точке
имеет в точке 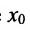 справа более высокий порядок роста, чем
справа более высокий порядок роста, чем 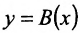 , если
, если 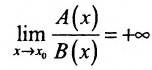
- Функции у = А(х) и у = В(х) имеют в точке
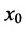 справа одинаковый порядок роста, если
справа одинаковый порядок роста, если 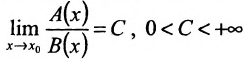
Например, функции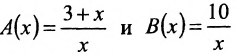 являются бесконечно большими одинакового роста в в точке х=0 как справа, так и слева, поскольку
являются бесконечно большими одинакового роста в в точке х=0 как справа, так и слева, поскольку 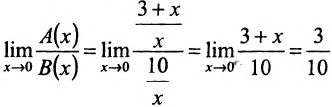
Точки непрерывности и точки разрыва
Предположим, что точка принадлежит области определения функции f и 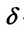 любая окрестность точки
любая окрестность точки 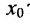 содержит отличные от
содержит отличные от 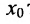 точки области определения функции f
точки области определения функции f
Определение 10.6.1. Функция f определенная на интервале (а, b), называется непрерывной в точке 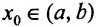 , если предел функции в точке Хоравен значению функции в точке
, если предел функции в точке Хоравен значению функции в точке 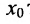 '
' 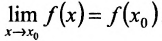 .
.
Используя определение предела функции в точке (см. п. 3.2.), это утверждение равносильно определению:
Определение J0.6.2. (по Коши) Функция f называется непрерывной в точке 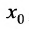 , если для любого положительного числа
, если для любого положительного числа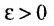
найдется отвечающее ему положительное число 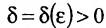 , такое, что для всех х, удовлетворяющих условию
, такое, что для всех х, удовлетворяющих условию 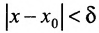 , выполняется неравенство
, выполняется неравенство 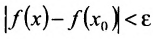 .
.
Учитывая, что 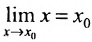 , то равенству
, то равенству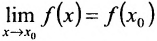 можно придать следующую форму:
можно придать следующую форму: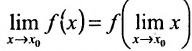 для непрерывной в точке
для непрерывной в точке 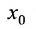 функции символ
функции символ 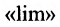 предельного перехода и символ «f» характеристики функции можно менять местами.
предельного перехода и символ «f» характеристики функции можно менять местами.
Пусть 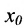 - любая точка интервала (а, b), на котором определена функция f. а
- любая точка интервала (а, b), на котором определена функция f. а 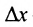 - произвольное число, такое, что значение аргумента
- произвольное число, такое, что значение аргумента 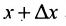 принадлежит интервалу (а, b). Это число
принадлежит интервалу (а, b). Это число 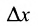 называется приращением аргумента. Разность
называется приращением аргумента. Разность 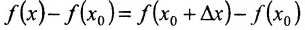 называется приращением функции, соответствующим приращению аргумента
называется приращением функции, соответствующим приращению аргумента 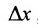 , и обозначается . Таким образом,
, и обозначается . Таким образом, 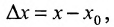
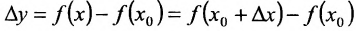 .
.
Справедливо утверждение:
для того, чтобы функция была непрерывной в точке  необходимо и достаточно, чтобы бесконечно малому приращению аргумента
необходимо и достаточно, чтобы бесконечно малому приращению аргумента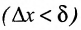 соответствовало бесконечно малое приращение функции, т.е.
соответствовало бесконечно малое приращение функции, т.е. 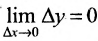 .
.
Примеры непрерывных функций:
- 1.
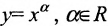 - степенная;
- степенная; - 2.
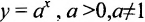 - показательная;
- показательная; - 3.
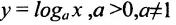 - логарифмическая;
- логарифмическая; - 4.
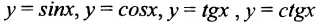 - тригонометрические;
- тригонометрические; - 5.
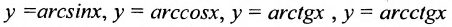 обратные тригонометрические функции.
обратные тригонометрические функции.
Пользуясь определениями предела слева и справа, можно сформулировать определение непрерывности слева и справа в точке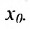 .
.
Определение 10.6.3. Пусть функция f определена на полуинтервале (а, b] (соответственно на полуинтервале на [а, b)) и 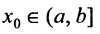
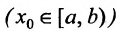 . Тогда функция f называется непрерывной слева (непрерывной справа) в точке
. Тогда функция f называется непрерывной слева (непрерывной справа) в точке 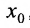 , если
, если 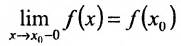 (соответственно
(соответственно 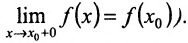 . Например, функция
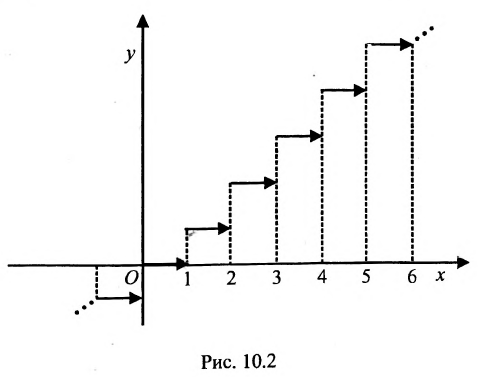
. Например, функция 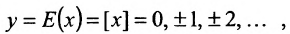 непрерывна справа и разрывна слева в точках х=n ( см. рис. 10.2).
непрерывна справа и разрывна слева в точках х=n ( см. рис. 10.2).
Определение 10.6.4. Пусть функция f, определена на интервале (а, b), кроме, быть может, точки 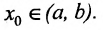 . Если функция f не непрерывна в точке
. Если функция f не непрерывна в точке 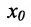 , то точка
, то точка 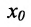 называется точкой разрыва функции.
называется точкой разрыва функции.
Определение 10.6.5. Если 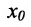 - точка разрыва функции f и существуют конечные пределы
- точка разрыва функции f и существуют конечные пределы 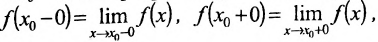 такие, что
такие, что 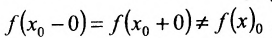 , то
, то 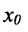 называется точкой устранимого разрыва. Если же
называется точкой устранимого разрыва. Если же 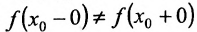 , то
, то 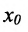 называется точкой разрыва первого рода, а величина
называется точкой разрыва первого рода, а величина 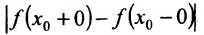 называется скачком функции f в точке
называется скачком функции f в точке 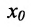 . Точка разрыва функции f не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода.
. Точка разрыва функции f не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода.
Из определения следует, что в устранимой точке разрыва функцию f можно доопределить или видоизменить, положив 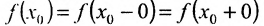 , что она будет непрерывна в точке
, что она будет непрерывна в точке 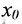 ,. В точках же разрыва второго рода по крайней мере один из пределов
,. В точках же разрыва второго рода по крайней мере один из пределов 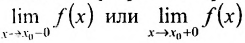 не существует или равен бесконечности.
не существует или равен бесконечности.
Например, функция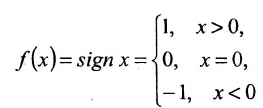 , имеет в точке
, имеет в точке  разрыв первого рода (рис. 10.3). Функция
разрыв первого рода (рис. 10.3). Функция 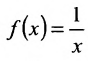 имеет в точке
имеет в точке 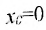 разрыв второго рода (рис. 10.4), так как
разрыв второго рода (рис. 10.4), так как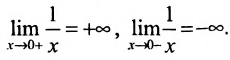
Пример:
Исследовать непрерывность функции: 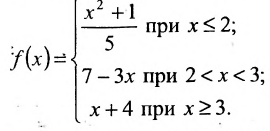 и определить характер точек разрыва, если они есть
и определить характер точек разрыва, если они есть
Решение:
Область определения функции - вся числовая ось. На интервалах (-оо; 2) и (2; 3)и(3; +°о) функция непрерывна. Поэтому разрывы возможны в точках х=2 и х=3, в которых изменяется аналитическое задание функции.
Найдем односторонние пределы функции в точке х=2:
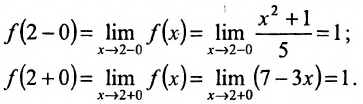
Значение функции в точке х=2 определяется первым аналитическим выражением. Поэтому 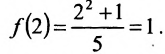 Так как
Так как 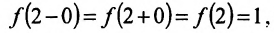 то в точке х=2 функция непрерывна.
то в точке х=2 функция непрерывна.
Рассмотрим точку x=3:
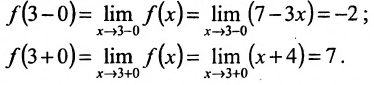
Предел справа не равен пределу слева, хотя они и конечны. Следовательно, в точке х=3 функция имеет разрыв первого рода (рис. 10.5). Скачок функции в точке разрыва равен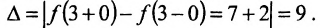
Свойства функций, непрерывных в точке
Арифметические операции над непрерывными функциями приводят снова к непрерывным функциям, т.е. справедлива следующая теорема:
Теорема 10.7.1. Если функции f и g непрерывны в точке 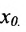 , то функции
, то функции 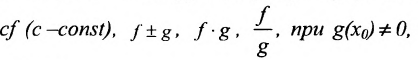 также непрерывны в точке
также непрерывны в точке 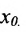 .
.
Доказательство. Пусть заданы две функции f и g непрерывные в точке 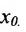 . Докажем, что
. Докажем, что 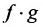 является функцией непрерывной. Поскольку предел произведения равен произведению пределов, если пределы сомножителей существуют (а они существуют, так как функции f и g непрерывны) и в силу непрерывности/и g, получим:
является функцией непрерывной. Поскольку предел произведения равен произведению пределов, если пределы сомножителей существуют (а они существуют, так как функции f и g непрерывны) и в силу непрерывности/и g, получим: 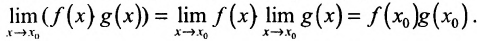
Это значит, в силу определения непрерывности функции, что функция 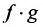 непрерывна в точке
непрерывна в точке 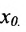 . Аналогично доказываются и остальные утверждения.
. Аналогично доказываются и остальные утверждения.
Функция, полученная в результате последовательного применения двух функций 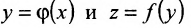 в определенном порядке, называется сложной функцией
в определенном порядке, называется сложной функцией 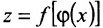 . Говорят, что сложная функция получена в результате суперпозиции двух функций. Ясно, что можно определять сложную функцию как результат и большего числа суперпозиций.
. Говорят, что сложная функция получена в результате суперпозиции двух функций. Ясно, что можно определять сложную функцию как результат и большего числа суперпозиций.
Пусть функция 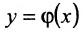 определена на множестве X, и пусть Y- множество ее значений. Допустим, что на множестве У задана функция
определена на множестве X, и пусть Y- множество ее значений. Допустим, что на множестве У задана функция 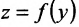 . Тогда на множестве X будет задана сложная функция
. Тогда на множестве X будет задана сложная функция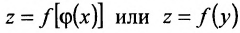 , где
, где 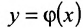 . Справедлива следующая теорема.
. Справедлива следующая теорема.
Теорема 10.7.2. Пусть функция 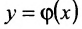 непрерывна в точке
непрерывна в точке 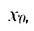 , а функция
, а функция 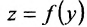 непрерывна в точке
непрерывна в точке 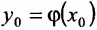 , тогда сложная функция
, тогда сложная функция 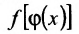 непрерывна в точке
непрерывна в точке 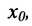 , т.е
, т.е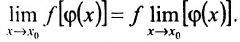
Доказательство. Так как функции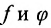 непрерывны, то сложная функция определена в некоторой окрестности точки
непрерывны, то сложная функция определена в некоторой окрестности точки 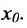 . Зададим произвольное
. Зададим произвольное 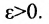 . Тогда, т.к. функция f непрерывна в точке
. Тогда, т.к. функция f непрерывна в точке 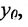 , то существует
, то существует 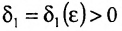 , что для всех у, удовлетворяющих условию
, что для всех у, удовлетворяющих условию 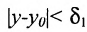 , выполняется неравенство
, выполняется неравенство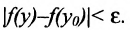 Для полученного
Для полученного 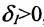 , в силу непрерывности функции
, в силу непрерывности функции 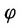 в точке
в точке 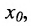 существует такое
существует такое 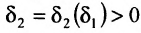 , что если
, что если 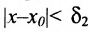 , то
, то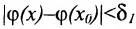 . Таким образом, если
. Таким образом, если 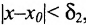 ,
,
То 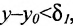 , а значит, и
, а значит, и 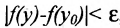 которое можно записать в виде
которое можно записать в виде 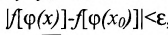 что и означает непрерывность сложной функции.
что и означает непрерывность сложной функции. 
Непрерывность обратной функции
Пусть функция 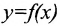 определена на отрезке [а, b] и пусть отрет зок
определена на отрезке [а, b] и пусть отрет зок 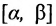 является множеством значений, причём каждому значению
является множеством значений, причём каждому значению 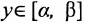 соответствует одно значение
соответствует одно значение 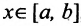 , для которого
, для которого 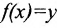 . Функция, определенная на
. Функция, определенная на 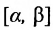 , ставящая каждому
, ставящая каждому 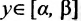 то значение
то значение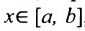 , для которого
, для которого 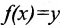 называется обратной для функции
называется обратной для функции 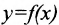 и обозначается
и обозначается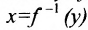 . Ясно, что если
. Ясно, что если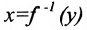 обратная для
обратная для 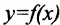 то и
то и 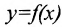 - обратная для
- обратная для 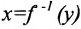 . Кроме того,
. Кроме того,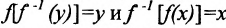 . Пример 10.8.1. Функция у=2х определена на [a, b]. Множество значений
. Пример 10.8.1. Функция у=2х определена на [a, b]. Множество значений 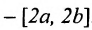 Тогда функция
Тогда функция 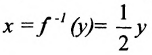 определенная на
определенная на 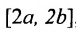 обратная для функции у=2х.
обратная для функции у=2х.
Теорема 10.8.1. Пусть функция у =f(x) возрастает (убывает) и непрерывна на [а, b], и 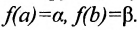 Тогда на отрезке
Тогда на отрезке 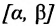 (соответственно
(соответственно 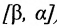 ) определена обратная для y=f(x) функция, которая возрастает (убывает) и непрерывна на указанном отрезке.
) определена обратная для y=f(x) функция, которая возрастает (убывает) и непрерывна на указанном отрезке.
Доказательство. Пусть задана возрастающая и непрерывная на [a, b] функция y=f(x). Из определения функции следует, что каждому [a, b], соответствует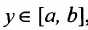 , а так y=f(x) возрастает, то каждому
, а так y=f(x) возрастает, то каждому 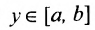 соответствует только одно
соответствует только одно 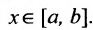 .
.
Пусть 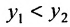 , где
, где 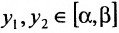 . Тогда
. Тогда 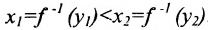 . Если бы
. Если бы 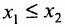 , то из неравенства
, то из неравенства 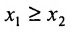 и из возрастания функции
и из возрастания функции 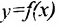 следует, что
следует, что 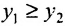 , что противоречит
, что противоречит 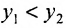 . Итак, мы доказали существование обратной возрастающей функции. Докажем, что она непрерывна. Для этого предположим, что она разрывна в точке
. Итак, мы доказали существование обратной возрастающей функции. Докажем, что она непрерывна. Для этого предположим, что она разрывна в точке 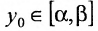 . Это значит, что предел справа либо предел слева не равен значению функции в точке, т.е.
. Это значит, что предел справа либо предел слева не равен значению функции в точке, т.е. 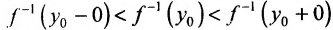 поскольку функция
поскольку функция 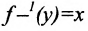 возрастает. Значит интервал
возрастает. Значит интервал 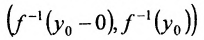 или
или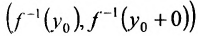 содержит значений
содержит значений 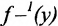 . А это противоречит тому, что любое число се [a,b] является значением функции
. А это противоречит тому, что любое число се [a,b] является значением функции 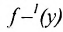 . Полученное противоречие и доказывает теорему
. Полученное противоречие и доказывает теорему 
Общие свойства непрерывных функций на отрезке: теоремы Вейерштрасса
Рассмотрим функцию 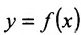 , заданную на отрезке [а,b].
, заданную на отрезке [а,b].
Определение 10.9.1. Функция называется непрерывной на отрезке [а,b] , если она непрерывна в каждой внутренней точке этого отрезка и непрерывна справа в точке а и непрерывна слева в точке b.
Теорема 10.9.1. (Первая теорема Вейерштрасса) Всякая непрерывная на отрезке функция ограничена.
Доказательство. Предположим, что существует непрерывная функция 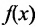 на отрезке [а,b], но не ограничена на нём. Это значит, что для любого
на отрезке [а,b], но не ограничена на нём. Это значит, что для любого 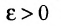 существует такая точка
существует такая точка 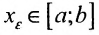 , что
, что 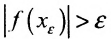 . Задаем последовательно
. Задаем последовательно 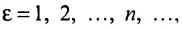 , получим последовательность
, получим последовательность 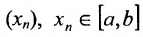 , для которых
, для которых 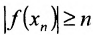 . Последовательность
. Последовательность 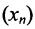 ограничена (она заключена на отрезке). Следовательно, из нее можно выделить сходящуюся подпоследовательность
ограничена (она заключена на отрезке). Следовательно, из нее можно выделить сходящуюся подпоследовательность 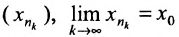 , для которой
, для которой 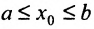 поскольку
поскольку 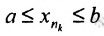
Но так как с одной стороны, получили, что 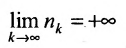 и
и 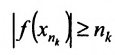 , то имеем
, то имеем 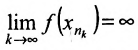 . С другой стороны, поскольку функция f непрерывна в точке
. С другой стороны, поскольку функция f непрерывна в точке 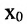 (она непрерывна на отрезке), то ее предел конечен
(она непрерывна на отрезке), то ее предел конечен 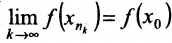 Таким образом, предположив, что функция f не ограничена, получили противоречие с тем, что она имеет предел в точке неограниченности. Значит, такое предположение неверно. Следовательно, непрерывная функция ограничена на отрезке.
Таким образом, предположив, что функция f не ограничена, получили противоречие с тем, что она имеет предел в точке неограниченности. Значит, такое предположение неверно. Следовательно, непрерывная функция ограничена на отрезке. 
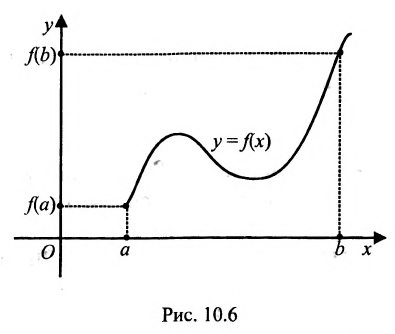
Рассмотрим функцию  , ограниченную на данном множестве X (рис. 10.7).
, ограниченную на данном множестве X (рис. 10.7).
Число М (m) называется точной верхней (точной нижней) гранью функции f на множестве X, если:
- для каждого значения
 выполняется неравенство;
выполняется неравенство; - для любого числа
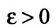 существует такое значение
существует такое значение 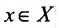 , что для соответствующего значения функции f(x) справедливо неравенство
, что для соответствующего значения функции f(x) справедливо неравенство 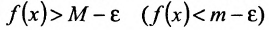 .
.
Точная верхняя (точная нижняя) грань М (m) функции 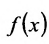 , на множестве обозначается символом
, на множестве обозначается символом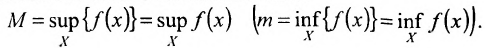
Пример:
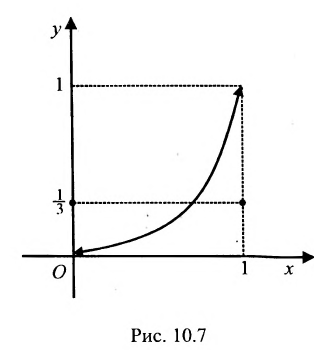
Рассмотрим на отрезке [0; 1] функцию f(x):
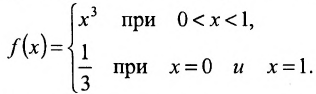
Эта функция ограничена на отрезке [0; 1] и имеет на нем точную верхнюю грань М=1 и точную нижнюю грань m=0. Однако эти грани недостижимы: среди точек отрезка [0; 1] не существует точек, значения функции в которых были бы равны нулю или единице.
Отметим, что эта функция не является непрерывной на отрезке [0; 1]. так как она имеет разрывы первого рода в точках х=0 и x=1.
Теорема 10.9.2. (Вторая теорема Вейергитрасса). Всякая непрерывная на отрезке функция имеет на этом отрезке как наибольшее, так и наименьшее значения.
Доказательство. Пусть функция определена и непрерывна на отрезке [а,b] и 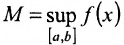 ; в силу теоремы 10.9.1. М- конечное число. Допустим, что функция f не достигает своей верхней грани М, т.е.
; в силу теоремы 10.9.1. М- конечное число. Допустим, что функция f не достигает своей верхней грани М, т.е. 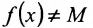 для всех х из отрезка [а, b].
для всех х из отрезка [а, b].
Тогда функция
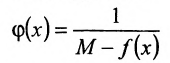
непрерывна на 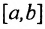 как частное от деления двух непрерывных функций с делителем, не равным нулю. Но разность
как частное от деления двух непрерывных функций с делителем, не равным нулю. Но разность 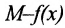 может быть сделана сколь угодно малой в силу определения верхней грани, т.е.
может быть сделана сколь угодно малой в силу определения верхней грани, т.е.
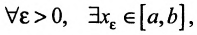
что
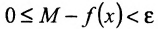 , и значит,
, и значит,
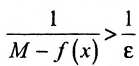
т.е. функция неограничена, что противоречит теореме 10.9.1, т.к.
неограничена, что противоречит теореме 10.9.1, т.к. 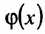 непрерывна. Полученное противоречие доказывает, что наше предположение о недостижимости точной верхней грани является неверным. Значит, непрерывная на отрезке функция достигает точной верхней грани на этом отрезке (см. рис. 10.8).
непрерывна. Полученное противоречие доказывает, что наше предположение о недостижимости точной верхней грани является неверным. Значит, непрерывная на отрезке функция достигает точной верхней грани на этом отрезке (см. рис. 10.8).  Аналогичные рассуждения проводятся и для нижней грани. Теорема доказана.
Аналогичные рассуждения проводятся и для нижней грани. Теорема доказана.
Промежуточные значения непрерывной функции на отрезке
Свойства функции, которые непрерывны в сколь угодно малой окрестности фиксированной точки области определения функции, относятся к локальным свойствам функции. Эти свойства характеризуют поведение функции при стремлении аргумента к исследуемой точке. Так, непрерывность функции в некоторой точке обрасти определения, является локальным свойством. Свойства же, связанные со всей областью определения функции относятся к глобальным свойствам. Например, монотонность функции на отрезке, непрерывность функции на отрезке являются глобальными свойствами функции. Теоремы Вейерштрасса относятся также к глобальным свойствам функции. Рассмотрим еще ряд глобальных свойств непрерывных функций.
Теорема 10.10.1. Если функция f непрерывна на отрезке [а,b] и 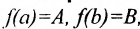 , то для любого значения С, заключенного между А и В, существует такая точка
, то для любого значения С, заключенного между А и В, существует такая точка 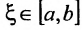 что
что
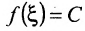
Доказательство. Пусть 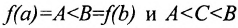 . Разделим отрезок [а,b] точкой
. Разделим отрезок [а,b] точкой 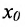 на два равных отрезка. Тогда либо
на два равных отрезка. Тогда либо 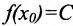 , и значит, искомая точка найдена:
, и значит, искомая точка найдена: 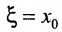 , либо
, либо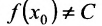 и тогда на концах одного из полученных отрезков функция f принимает значения лежащие по разные стороны от числа С, точнее - на левом конце значение, меньшее С, на правом - большее.
и тогда на концах одного из полученных отрезков функция f принимает значения лежащие по разные стороны от числа С, точнее - на левом конце значение, меньшее С, на правом - большее.
Обозначим этот отрезок 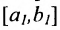 и разобьём его снова на два равных отрезка и выберем тот, на концах которого функция f принимает значения большее и меньшее С и т.д.
и разобьём его снова на два равных отрезка и выберем тот, на концах которого функция f принимает значения большее и меньшее С и т.д.
В результате либо через конечное число шагов придем к искомой точке 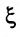 в которой
в которой 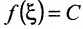 , либо получим последовательность вложенных отрезков
, либо получим последовательность вложенных отрезков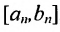 , по длине стремящихся к нулю и таких, что
, по длине стремящихся к нулю и таких, что

Тогда существует точка 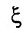 - общая точка системы отрезков
- общая точка системы отрезков
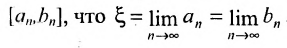
Поэтому, в силу непрерывности функции
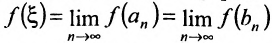
Но из (10.10.1) получим, что 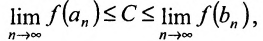
откуда вытекает, что 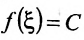 .
.
Следствие 10.10.1. Если функция непрерывна на отрезке и на концах отрезка принимает значения разных знаков, то на этом отрезке существует точка, в которой функция обращается в нуль.,
Доказательство.
Не ограничивая общности рассуждений мож но считать, что 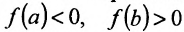 . Так как число нуль заключен между значениями
. Так как число нуль заключен между значениями 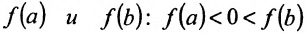 , то согласно теореме 10.10.1 на отрезке [а; b] найдется такая точка с, что f(c)=0.
, то согласно теореме 10.10.1 на отрезке [а; b] найдется такая точка с, что f(c)=0.
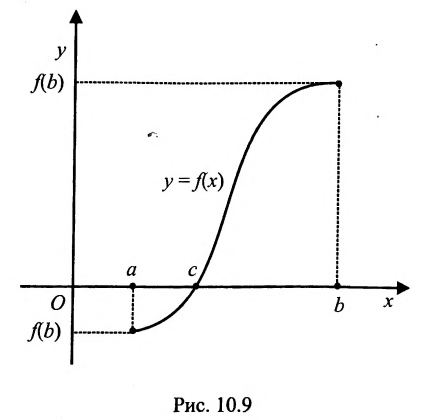
Заметим, что точка с - внутренняя точка отрезка [а; b], так как из непрерывности функции f(x) на отрезке [а; b] и из условия вытекает, что найдется правая
вытекает, что найдется правая 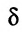 -полуокрестность точки а, в пределах которой
-полуокрестность точки а, в пределах которой 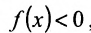 , и левая
, и левая 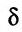 -полуокрестность точки Ь, в пределах которой
-полуокрестность точки Ь, в пределах которой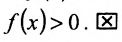
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Исследование поведения функций
- Предел и непрерывность функции двух переменны
- Определители второго и третьего порядков и их свойства
- Метод Гаусса - определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве