
Функциональные преобразования двухмерных случайных величин с примерами решения
Функциональные преобразования двухмерных случайных величин:
Пусть 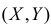
где функции 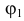 и
и 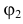 непрерывно дифференцируемы и отображение (2.15.1) взаимно однозначно, т.е. существуют функции
непрерывно дифференцируемы и отображение (2.15.1) взаимно однозначно, т.е. существуют функции 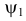 и
и 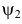 такие, что
такие, что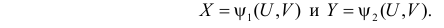
Если 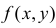 – функция плотности вероятности случайного вектора
– функция плотности вероятности случайного вектора 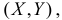 а
а 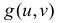 – функция плотности вероятности случайного вектора
– функция плотности вероятности случайного вектора 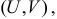 то
то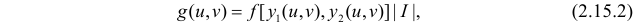
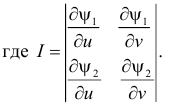
Пример:
Случайный вектор 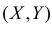 имеет плотность вероятности
имеет плотность вероятности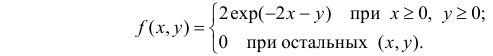
Найти плотность вероятности случайного вектора 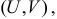 если
если 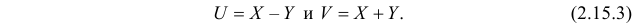
Решение. Найдем обратное к (2.15.3) преобразование: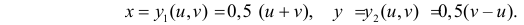
Заметим, что из условия неотрицательности 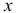 и
и 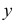 следует:
следует: 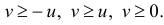 Так как
Так как
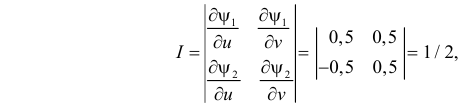
то функция плотности вероятности случайного вектора 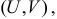 в соответствии с формулой (2.15.2), имеет вид
в соответствии с формулой (2.15.2), имеет вид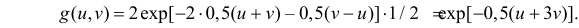
Ответ. 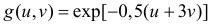 при
при 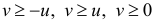 и
и 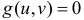 при остальных
при остальных 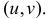
Пример:
Случайные величины X и Y независимы и имеют нормальные законы распределения с нулевыми средними значениями и одинаковыми дисперсиями 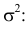
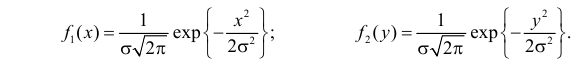
Пусть X и Y декартовы координаты случайного вектора 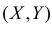 . Производится переход к полярным координатам по формулам
. Производится переход к полярным координатам по формулам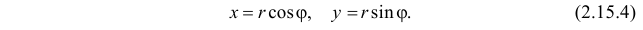
Требуется найти функцию плотности вероятности случайного вектора 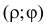 и функции плотности вероятности компонент этого вектора
и функции плотности вероятности компонент этого вектора 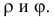
Решение. Так как X и Y независимы, то плотность вероятности случайного вектора 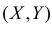 имеет вид
имеет вид
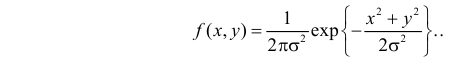
Якобиан преобразования (2.15.4) равен 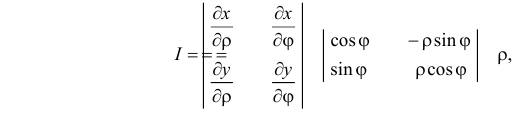
по формуле (2.15.2) получаем 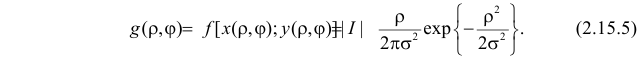
Плотность вероятности (2.15.5) позволяет вычислить маргинальные плотности вероятности. Плотность распределения величины 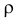
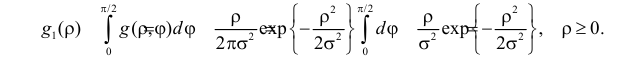
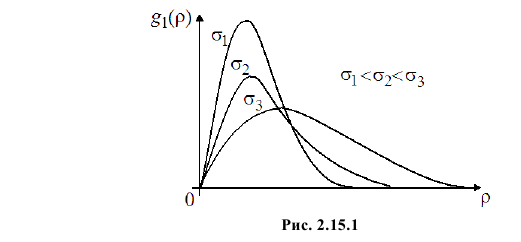
Это распределение известно как распределение Релея (Rayleigh distribution). График его плотности вероятности для нескольких значений параметра s приведен на рис. 2.15.1.
Плотность распределения случайной величины 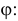
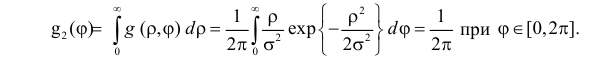
Это равномерное распределение на отрезке 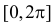
Ответ. 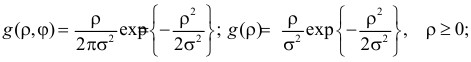
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |