Функции y=tg x и y=ctg x - их свойства, графики и примеры решения

Содержание:

Определение функции y=tg x

Определение:

Зависимость, при которой каждому действительному числу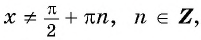

Пример:

Определите, принадлежит ли графику функции 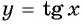точка:

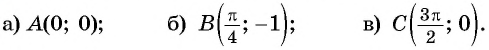
Решение:

а) Подставим в формулу 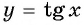значение аргумента 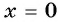и найдем соответствующее значение функции 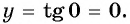Полученное значение функции равно ординате точки 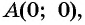значит, точка 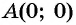принадлежит графику функции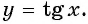

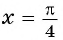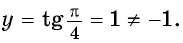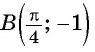б) При получим Точка не принадлежит графику функции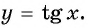

в) При 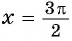получим 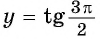— не существует. Точка 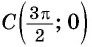не принадлежит графику функции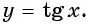

Определение функции y=ctg x

Определение:

Зависимость, при которой каждому действительному числу 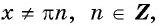соответствует значение 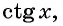называется функцией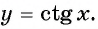

Пример:

Верно ли, что график функции 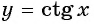проходит через точку:

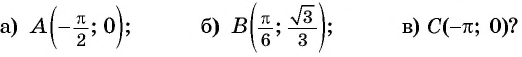
Решение:

а) Подставим в формулу 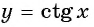значение аргумента 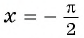и найдем соответствующее значение функции 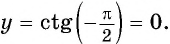Полученное значение функции равно ординате точки 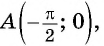значит, график функции 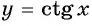проходит через точку 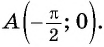Верно.

б) При 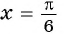получим 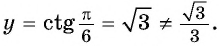График функции 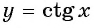не проходит через точку 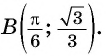Неверно.

в) При 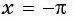получим 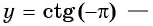не существует. График функции 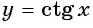не проходит через точку 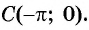Неверно.

Свойства функций y=tg x и y=ctg x

Рассмотрим свойства этих функций:

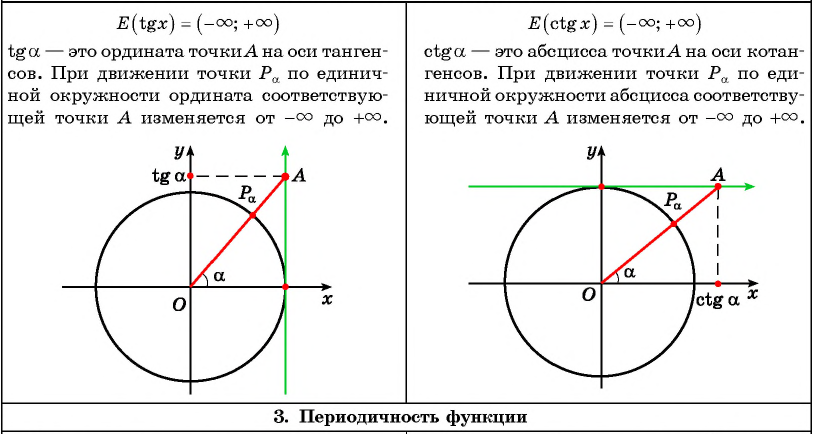
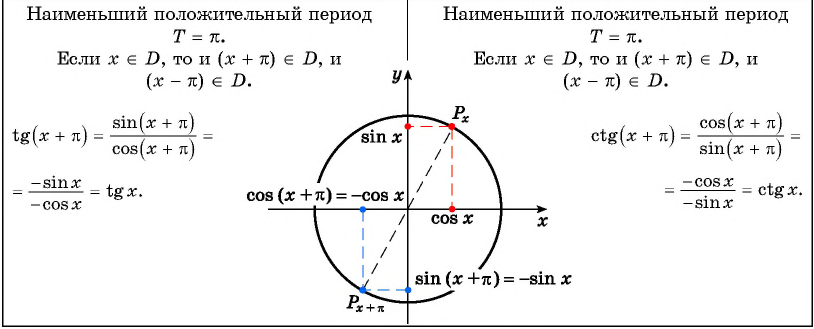
График функции y=tg x

График функции 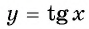изображен на рисунке 88. Он называется тангенсоидой.

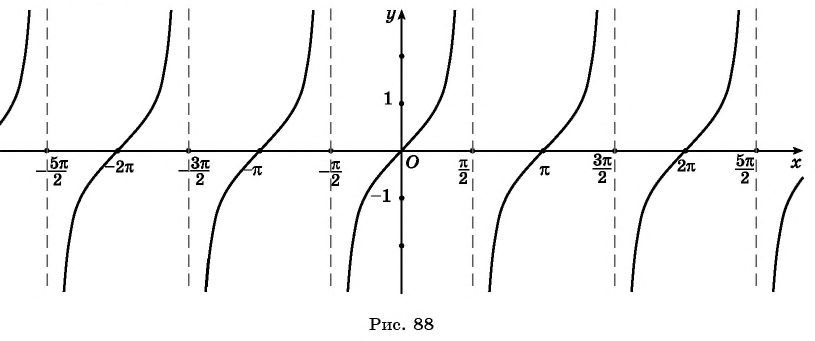
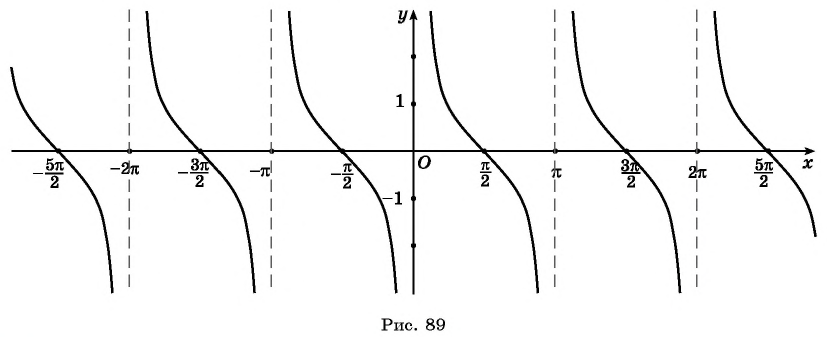
График функции y=ctg x

График функции 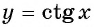изображен на рисунке 89. Этот график может быть получен путем преобразования графика функции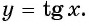

Примеры заданий и их решения

Пример №1

Найдите область определения функции:

Решение:

а) Так как область определения функции 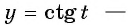это все действительные числа, кроме чисел вида 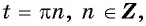то 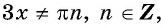значит, 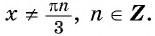Таким образом, область определения данной функции — это все действительные числа, кроме чисел вида

б) Областью определения функции 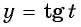является множество всех действительных чисел, кроме чисел вида 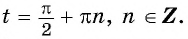Значит, 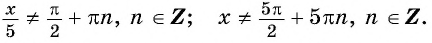Область определения данной функции — это все действительные числа, кроме чисел вида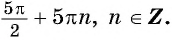

Пример №2

Найдите множество значений функции:

Решение:

а) Так как множество значений функции 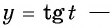это множество всех действительных чисел, то и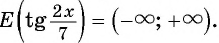

б) Так как множество значений функции 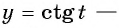это множество всех действительных чисел, то и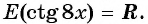

Пример №3

Используя свойство периодичности функций 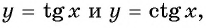найдите:

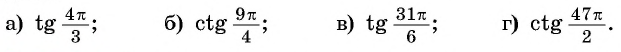
Решение:

Так как число 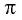является наименьшим положительным периодом функци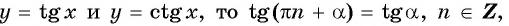й и 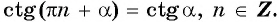Тогда:

• Заказать решение задач по высшей математике

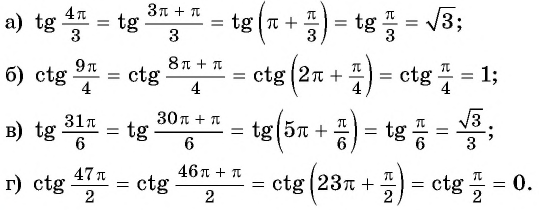
Пример №4

Используя свойство нечетности функций 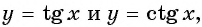найдите:

Решение:

Так как функции 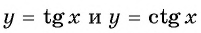являются нечетными, то 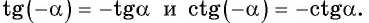Тогда:

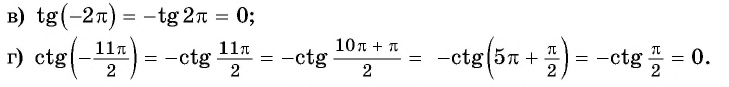
Пример №5

Определите знак произведения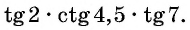

Решение:

Так как 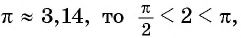т. е. угол 2 радиана принадлежит промежутку 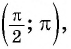на котором функция 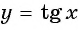принимает отрицательные значения, значит,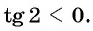

Угол 4,5 радиана принадлежит промежутку 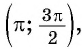на котором функция 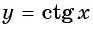принимает положительные значения, значит,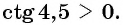

Угол 7 радиан принадлежит промежутку 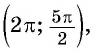на котором функция 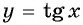принимает положительные значения, т. е. 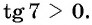Значит,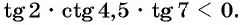

Пример №6

Что больше: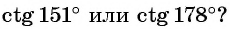

Решение:

Поскольку углы 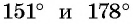принадлежат промежутку 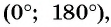на котором функция 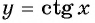убывает и 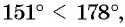то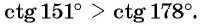

Пример №7

Постройте график функции:

Решение:

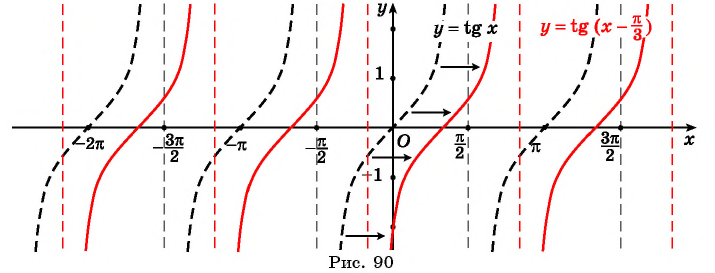
а) График функции 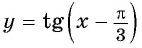получаем сдвигом графика функции 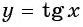вдоль оси абсцисс на 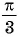вправо (рис. 90).

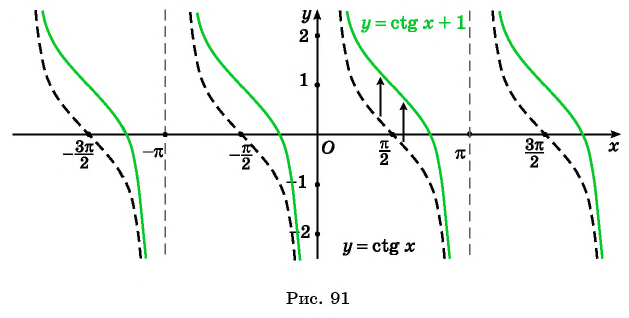
б) График функции 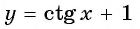получаем сдвигом графика функции 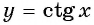вдоль оси ординат на 1 единицу вверх (рис. 91).