
Функции случайных величин - определение и вычисление с примерами решения
Содержание:
Функции случайных величин:
Пусть 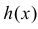
I. Пусть Х – дискретная случайная величина. Если функция 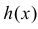 в области возможных значений Х монотонна, то величина Н примет значение
в области возможных значений Х монотонна, то величина Н примет значение 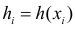 тогда и только тогда, когда
тогда и только тогда, когда 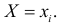 Следовательно, возможными значениями Н будут значения
Следовательно, возможными значениями Н будут значения 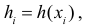 и этим значениям соответствуют вероятности
и этим значениям соответствуют вероятности 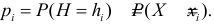
II. Если 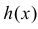 немонотонна и существует несколько значений
немонотонна и существует несколько значений 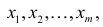 при которых
при которых 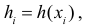 то
то 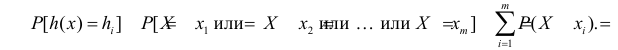
Следовательно, для нахождения закона распределения случайной величины 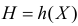 нужно вычислить все ее значения, расположить их в порядке возрастания, отбрасывая повторяющиеся, и каждому из полученных значений
нужно вычислить все ее значения, расположить их в порядке возрастания, отбрасывая повторяющиеся, и каждому из полученных значений 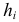 приписать вероятность, равную сумме вероятностей тех значений Х, для которых
приписать вероятность, равную сумме вероятностей тех значений Х, для которых 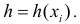
Пример:
Дискретная случайная величина имеет закон распределения
Найти закон распределения 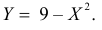
Решение. Вероятность возможного значения 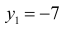 равна вероятности события Х = 4, т.е. 0,1. Вероятность возможного значения
равна вероятности события Х = 4, т.е. 0,1. Вероятность возможного значения 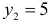 равна сумме вероятностей несовместных событий
равна сумме вероятностей несовместных событий 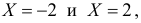 т.е.
т.е. 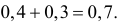 Вероятность значения
Вероятность значения 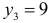 равна
равна 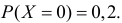 Искомое распределение имеет вид
Искомое распределение имеет вид 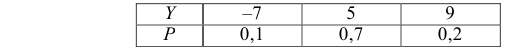
Пример:
Случайные величины Х1 и Х2 независимы и имеют каждая закон распределения:
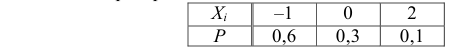
Найти законы распределения случайных величин: 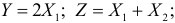
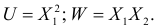 Найти математические ожидания этих величин.
Найти математические ожидания этих величин.
Решение. Функция 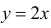 монотонна. Поэтому Y может принимать значения –2, 0, 4 с вероятностями, равными вероятностям соответствующих значений Х. Отсюда
монотонна. Поэтому Y может принимать значения –2, 0, 4 с вероятностями, равными вероятностям соответствующих значений Х. Отсюда

и 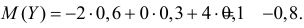 Найдем возможные значения Z:
Найдем возможные значения Z:

Суммируя вероятности повторяющихся значений Z, получаем закон распределения:

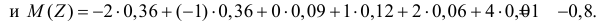
Случайная величина U принимает значения: 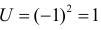 с вероятностью 0,6;
с вероятностью 0,6; 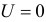 с вероятностью 0,3 и
с вероятностью 0,3 и 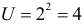 с вероятностью 0,1. Поэтому закон распределения U имеет вид:
с вероятностью 0,1. Поэтому закон распределения U имеет вид:

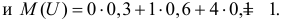 Найдем возможные значения
Найдем возможные значения 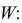

Суммируя вероятности повторяющихся значений W, получаем закон распределения:

Ответ. 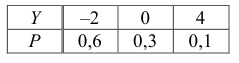
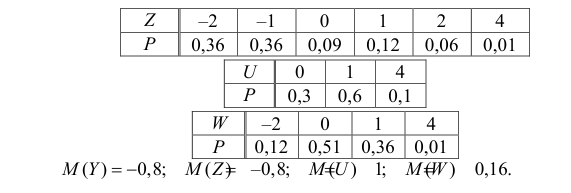
Решение функции случайных величин
Пример:
В каждой игре игрок может выиграть один рубль с вероятностью 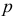 и проиграть рубль с вероятностью
и проиграть рубль с вероятностью 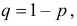 т.е. результат
т.е. результат 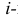 й игры можно охарактеризовать случайной величиной
й игры можно охарактеризовать случайной величиной 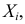 которая имеет закон распределения
которая имеет закон распределения
Пусть S – результат 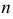 игр, т.е.
игр, т.е. 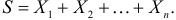 Требуется найти
Требуется найти 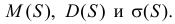
Решение. По свойству математических ожиданий 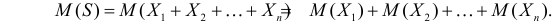
Так как 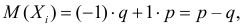 то
то 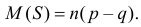 В силу независимости случайных величин
В силу независимости случайных величин 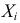
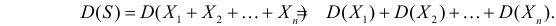
Так как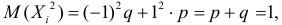 то
то 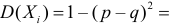
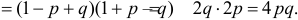 Поэтому
Поэтому 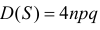 и
и 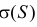
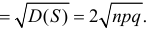
Ответ. 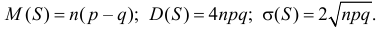
III. Рассмотрим монотонную функцию от непрерывной случайной величины Х. Предположим, что функция 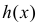 монотонна и непрерывна вместе со своей производной в области возможных значений случайной величины Х. Пусть Х имеет непрерывную функцию плотности вероятности
монотонна и непрерывна вместе со своей производной в области возможных значений случайной величины Х. Пусть Х имеет непрерывную функцию плотности вероятности 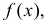 а величина
а величина 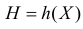 имеет непрерывную функцию плотности вероятности
имеет непрерывную функцию плотности вероятности 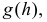 которую предстоит найти.
которую предстоит найти.
Для малых 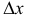 вероятность
вероятность 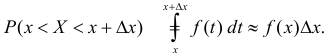 Соответственно
Соответственно 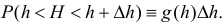 Функция
Функция 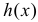 монотонна, поэтому каждый интервал
монотонна, поэтому каждый интервал 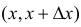 отображается взаимно однозначно на некоторый интервал
отображается взаимно однозначно на некоторый интервал 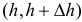 (см. рис. 2.11.1).
(см. рис. 2.11.1).
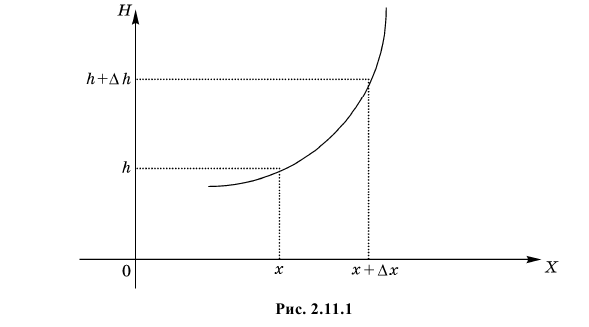
Значит, события 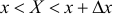 и
и 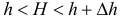 эквивалентны и вероятности этих событий равны
эквивалентны и вероятности этих событий равны
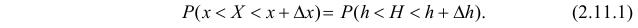
Поэтому 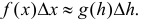 Последнее равенство в пределе при
Последнее равенство в пределе при 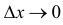 становится точным равенством
становится точным равенством 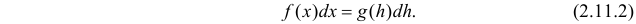
Из дифференцируемости и монотонности функции 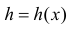 следует существование обратной функции
следует существование обратной функции 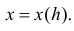 Подставляя эту функцию и ее дифференциал
Подставляя эту функцию и ее дифференциал 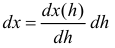 равенство (2.11.2), получим
равенство (2.11.2), получим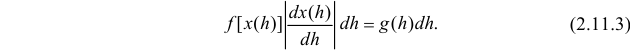
Знак модуля взят потому, что в левой части равенства (2.11.3) стоит неотрицательная величина, а производная функции 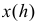 может оказаться отрицательной. Сравнивая левую и правую части равенства (2.11.3), приходим к выводу, что
может оказаться отрицательной. Сравнивая левую и правую части равенства (2.11.3), приходим к выводу, что
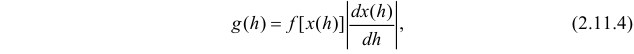
Пример:
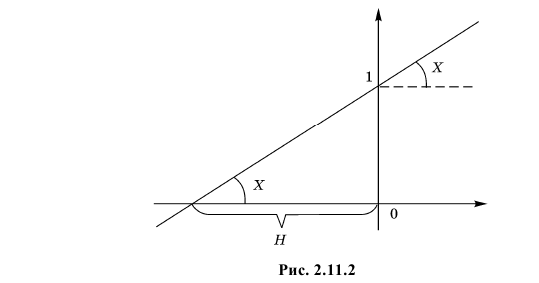
Прямая линия вращается в плоскости и ось ее вращения находится в точке с координатами (0,1). Прямая приводится во вращение, которое останавливается под действием сил трения. При остановке равновозможно любое положение прямой, т.е. угол Х (рис. 2.11.2) имеет равномерное распределение в отрезке 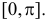 Найти закон распределения точки пересечения прямой с осью абсцисс.
Найти закон распределения точки пересечения прямой с осью абсцисс.
Решение. Обозначим координату точки пересечения прямой с осью абсцисс через Н. Очевидно, что Н является функцией от Х. Из рис. 2.11.2 видно, что значения случайных величин Х и Н связаны соотношением 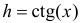 или
или 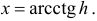 Откуда
Откуда 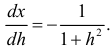
Случайная величина Х равномерно распределена в отрезке 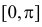 с плотностью вероятности
с плотностью вероятности 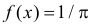 при
при 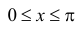 и
и 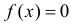 при остальных
при остальных 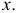 Из формулы (2.11.4) имеем
Из формулы (2.11.4) имеем 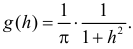 Это плотность вероятности закона распределения Коши.
Это плотность вероятности закона распределения Коши.
Ответ. 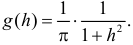
Пример:
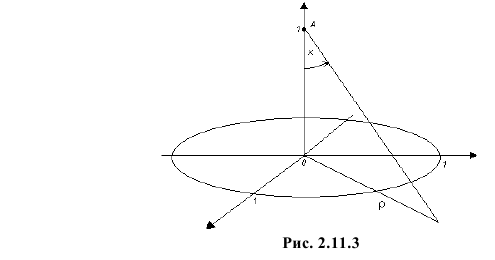
В точке 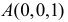 на вертикальной оси находится источник корпускулярного излучения. (Траектории частиц, вылетающих из точки А, – прямые линии.) Полагаем интенсивность излучения по всем направлениям одинаковой. Требуется найти распределение расстояния от начала координат до точки попадания частицы в горизонтальную плоскость. Требуется найти также вероятность попадания частицы в круг на горизонтальной плоскости радиусом
на вертикальной оси находится источник корпускулярного излучения. (Траектории частиц, вылетающих из точки А, – прямые линии.) Полагаем интенсивность излучения по всем направлениям одинаковой. Требуется найти распределение расстояния от начала координат до точки попадания частицы в горизонтальную плоскость. Требуется найти также вероятность попадания частицы в круг на горизонтальной плоскости радиусом 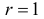 с центром в начале координат.
с центром в начале координат.
Решение. Пусть 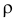 – расстояние от начала координат до точки попадания частицы в горизонтальную плоскость. Для угла X (см. рис. 2.11.3) равновозможны все значения в отрезке
– расстояние от начала координат до точки попадания частицы в горизонтальную плоскость. Для угла X (см. рис. 2.11.3) равновозможны все значения в отрезке 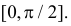
Поэтому случайная величина X имеет функцию плотности вероятности 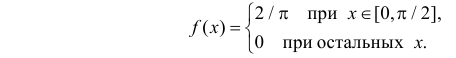
Заметим, что 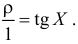 Так как обратная функция имеет вид
Так как обратная функция имеет вид 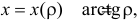 то по формуле (2.11.4)
то по формуле (2.11.4)

Вероятность попадания частицы в круг на горизонтальной плоскости радиусом 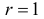 с центром в начале координат равна
с центром в начале координат равна 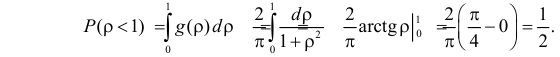
Ответ. 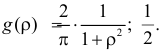
Пример:
Пусть 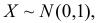 а
а 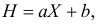 где
где 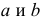 – некоторые постоянные. Найти закон распределения случайной величины Н.
– некоторые постоянные. Найти закон распределения случайной величины Н.
Решение. Из равенства 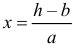 получаем, что
получаем, что 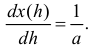 Так как
Так как 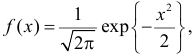 то по формуле (2.11.4) имеем
то по формуле (2.11.4) имеем 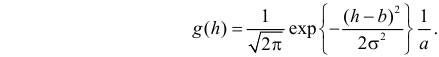
Значит 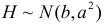 при
при 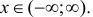
Ответ. 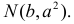
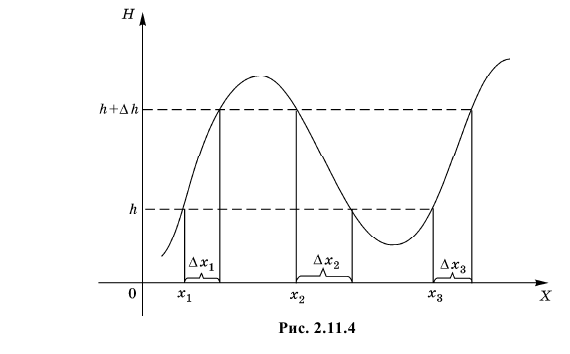
IV. Если функция 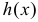 немонотонна, то вместо исходного равенства (2.11.1) имеем равенство (см. рис. 2.11.4)
немонотонна, то вместо исходного равенства (2.11.1) имеем равенство (см. рис. 2.11.4)
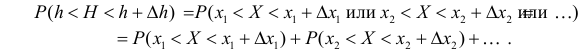
Каждое слагаемое в этом равенстве соответствует отдельному интервалу монотонности функции 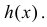 Повторяя рассуждения пункта III для каждого интервала монотонности, можно показать, что
Повторяя рассуждения пункта III для каждого интервала монотонности, можно показать, что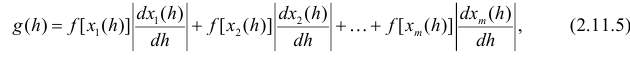
где 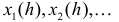 – функции, обратные к
– функции, обратные к 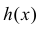 на соответствующих интервалах монотонности.
на соответствующих интервалах монотонности.
Пример:
Случайная величина X имеет плотность вероятности 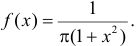 Найти плотность вероятности случайной величины
Найти плотность вероятности случайной величины 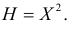
Решение. Функция 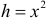 немонотонная. На интервале
немонотонная. На интервале 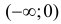 она убывает, а на интервале
она убывает, а на интервале 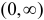 возрастает. Обратные функции имеют вид соответственно
возрастает. Обратные функции имеют вид соответственно 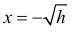 и
и 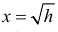 . В соответствии с формулой (2.11.5) имеем
. В соответствии с формулой (2.11.5) имеем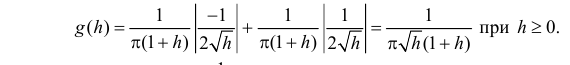
Ответ. 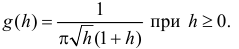
V. Рассмотрим смешанную случайную величину Х, функция распределения которой имеет точки разрыва 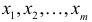 со скачками соответственно
со скачками соответственно 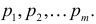 K Это означает, что Х, помимо возможных значений нулевой вероятности, имеет значения
K Это означает, что Х, помимо возможных значений нулевой вероятности, имеет значения 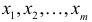 с отличными от нуля вероятностями
с отличными от нуля вероятностями 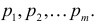
В этом случае плотность распределения вероятностей в точках 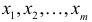 обращается в бесконечность, т.е. формально не существует. Эту трудность можно обойти, если воспользоваться дельта-функцией
обращается в бесконечность, т.е. формально не существует. Эту трудность можно обойти, если воспользоваться дельта-функцией 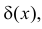 которая понимается как производная (в обобщенном смысле) от функции единичного скачка
которая понимается как производная (в обобщенном смысле) от функции единичного скачка 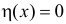 при
при 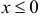 и
и 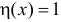 при
при 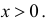 Наглядно
Наглядно 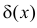 можно представить себе плотностью распределения «масс», при которой в точке
можно представить себе плотностью распределения «масс», при которой в точке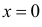 сосредоточена единичная масса, а масса во всех остальных точках равна нулю. Поэтому
сосредоточена единичная масса, а масса во всех остальных точках равна нулю. Поэтому
для всех непрерывных функций.
Функцию распределения смешанной случайной величины можно разложить на непрерывную и скачкообразную компоненты: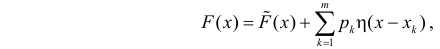
где 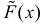 – непрерывная функция, которая не убывает и изменяется от 0 до
– непрерывная функция, которая не убывает и изменяется от 0 до 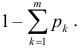 Тогда
Тогда 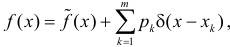 и формула (2.11.4) примет вид
и формула (2.11.4) примет вид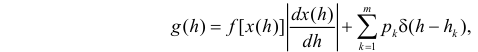
где 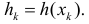
Пример:
Случайная величина X имеет закон распределения Коши с функцией плотности вероятности 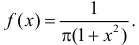 Случайная величина
Случайная величина 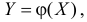 где функция
где функция 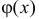 задана графически (см. рис. 2.11.5). Найти плотность вероятности величины Y.
задана графически (см. рис. 2.11.5). Найти плотность вероятности величины Y.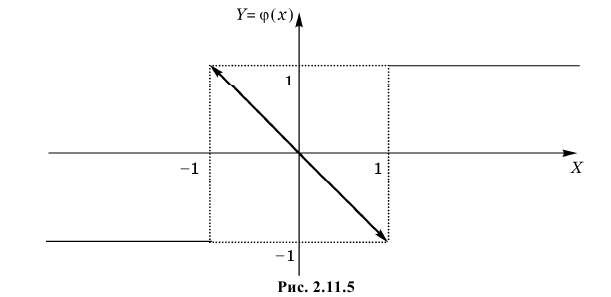
Решение. Из графика функции 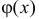 видно, что значения
видно, что значения 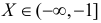 преобразуются в значение
преобразуются в значение 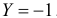 . Поэтому
. Поэтому 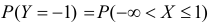
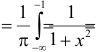
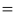
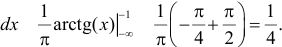 Аналогично
Аналогично 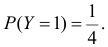
На интервале (-1,1) - функция 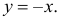 Обратная функция:
Обратная функция: 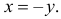 Поэтому
Поэтому 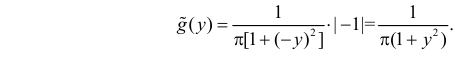
Окончательно с учетом значений, имеющих ненулевые вероятности, получаем 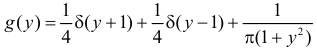 при
при 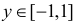 и
и 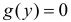 при
при 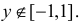
Ответ. 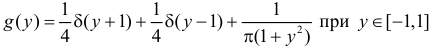
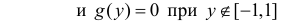 .
.
Замечание. Если нас интересуют только математическое ожидание и дисперсия случайной величины 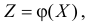 то нет необходимости предварительно находить закон распределения этой случайной величины. Можно вычислить
то нет необходимости предварительно находить закон распределения этой случайной величины. Можно вычислить 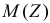 и
и 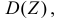 используя закон распределения случайной величины X, по формулам
используя закон распределения случайной величины X, по формулам
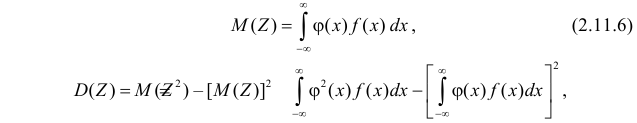
если X – непрерывная случайная величина с функцией плотности вероятности 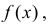 и по формулам
и по формулам
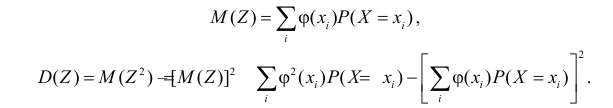
если X – дискретная случайная величина.
Пример:
Отрезок 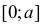 произвольным образом делится на две части (все положения точки деления в этом отрезке одинаково возможны). Полученные части отрезка составляют две стороны прямоугольника. Найти среднее значение его площади и дисперсию этой площади.
произвольным образом делится на две части (все положения точки деления в этом отрезке одинаково возможны). Полученные части отрезка составляют две стороны прямоугольника. Найти среднее значение его площади и дисперсию этой площади.
Решение. Обозначим длину одной из частей отрезка через X, тогда другая часть отрезка имеет длину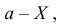 а площадь прямоугольника равна
а площадь прямоугольника равна 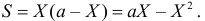 Так как все положения точки деления в отрезке одинаково возможны, то X имеет равномерное распределение на отрезке
Так как все положения точки деления в отрезке одинаково возможны, то X имеет равномерное распределение на отрезке 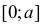 с функцией плотности вероятности
с функцией плотности вероятности 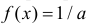 при
при 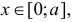 и
и 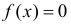 при остальных
при остальных 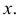 Поэтому среднее значение площади прямоугольника равно по формуле (2.11.6)
Поэтому среднее значение площади прямоугольника равно по формуле (2.11.6)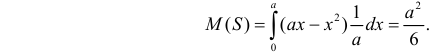
Дисперсия площади равна 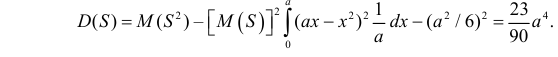
Ответ. 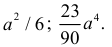
Функции нескольких случайных аргументов
Свертка
Пусть 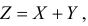 где случайные величины X и Y независимы и имеют функции плотности вероятности
где случайные величины X и Y независимы и имеют функции плотности вероятности 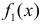 и
и 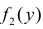 соответственно. Случайная величина Z имеет функцию плотности вероятности
соответственно. Случайная величина Z имеет функцию плотности вероятности 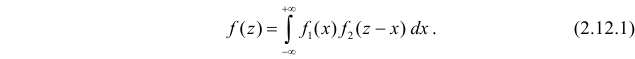
Выражение в правой части (2.12.1) называется свёрткой функций плотности вероятности 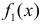 и
и 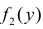 . Если случайные величины X и Y неотрицательны, то формула (2.12.1) имеет вид:
. Если случайные величины X и Y неотрицательны, то формула (2.12.1) имеет вид: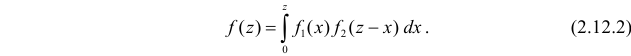
Пример №1
Пусть случайные величины X1 и X2 независимы и равномерно распределены на отрезках [0,2] и [0,3] соответственно. Найти закон распределения случайной величины 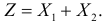
Решение. Все значения случайной величины X1 равновозможны в отрезке [0,2], поэтому ее плотность вероятности 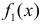 во всех точках этого отрезка должна быть одинакова, т.е. постоянна. Значение этой постоянной находим из условия, что интеграл от функции плотности вероятности по всем возможным значениям случайной величины равен единице. Итак, случайная величина X1 имеет функцию плотности вероятности
во всех точках этого отрезка должна быть одинакова, т.е. постоянна. Значение этой постоянной находим из условия, что интеграл от функции плотности вероятности по всем возможным значениям случайной величины равен единице. Итак, случайная величина X1 имеет функцию плотности вероятности 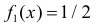 при
при 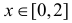 и
и 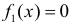 при остальных
при остальных 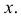 Из тех же соображений случайная величина X2 имеет плотность вероятности
Из тех же соображений случайная величина X2 имеет плотность вероятности 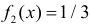 при
при 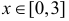 и
и 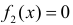 при остальных
при остальных 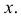 Так как X1 и X2 неотрицательны, то функцию плотности вероятности
Так как X1 и X2 неотрицательны, то функцию плотности вероятности 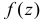 случайной величины
случайной величины 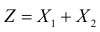 можно найти по формуле (2.12.2).
можно найти по формуле (2.12.2).
При 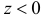 произведение функций
произведение функций 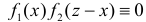 и поэтому из формулы (2.12.2) следует, что
и поэтому из формулы (2.12.2) следует, что 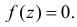 При
При 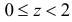 (см. рис. 12.1)
(см. рис. 12.1) 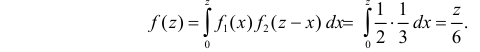
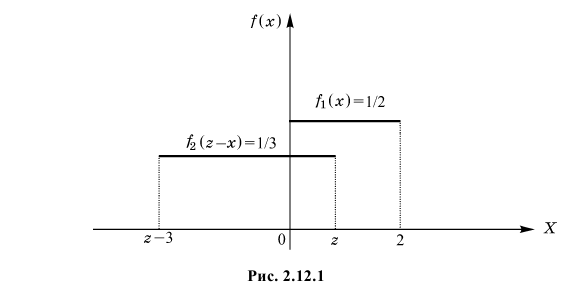
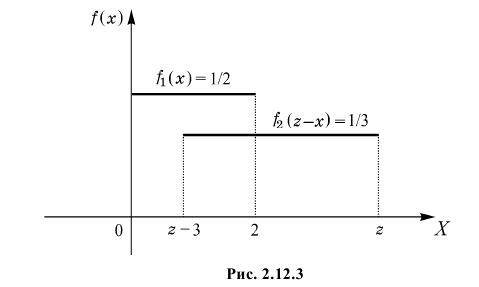
При 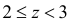 получаем (см. рис. 2.12.2)
получаем (см. рис. 2.12.2)
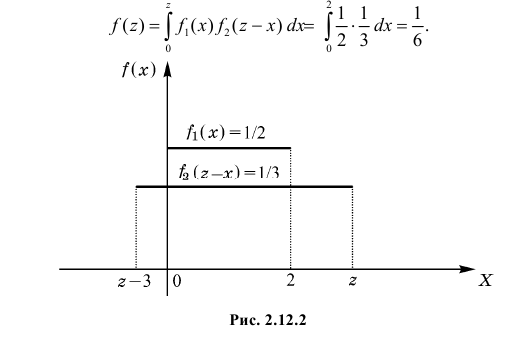
При 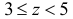 (см. рис. 2.12.3)
(см. рис. 2.12.3)
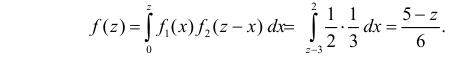
При 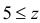 функция
функция 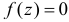 так как в формуле (2.12.2) под знаком интеграла произведение
так как в формуле (2.12.2) под знаком интеграла произведение 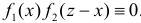
Итак, 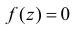 при
при 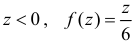 при
при 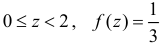 при
при 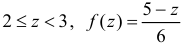 при
при 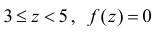 при
при 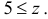 График функции плотности вероятности
График функции плотности вероятности 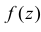 изображен на рис. 2.12.4. Закон распределения с такой плотностью вероятности иногда называют трапециевидным.
изображен на рис. 2.12.4. Закон распределения с такой плотностью вероятности иногда называют трапециевидным.
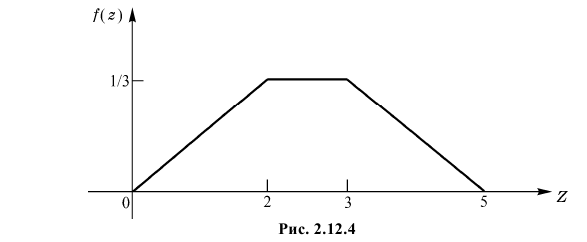
Ответ. 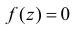 при
при 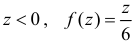 при
при 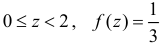 при
при 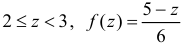 при
при 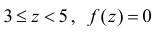 при
при 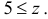
Замечание. Для 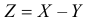 формула (2.12.1) имеет вид
формула (2.12.1) имеет вид 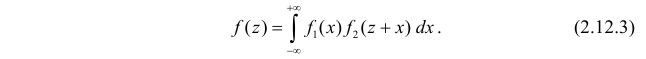
Пример №2
Пусть случайные величины X1 и X2 независимы и каждая имеет геометрический закон распределения: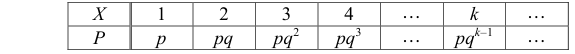
Требуется найти закон распределения случайной величины 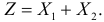
Решение. Очевидно, что 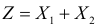 может принимать значения 2, 3, 4,… . В соответствии с формулой (2.12.4)
может принимать значения 2, 3, 4,… . В соответствии с формулой (2.12.4)
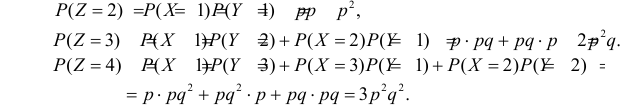
Закономерность образования вероятностей для Z в достаточной степени проявилась. Можно предположить, что 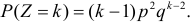 Вместо рассуждений по методу математической индукции можно просто заметить, что при вычислении каждой следующей вероятности добавляется еще одно слагаемое и в каждом слагаемом добавляется множитель q. Поэтому
Вместо рассуждений по методу математической индукции можно просто заметить, что при вычислении каждой следующей вероятности добавляется еще одно слагаемое и в каждом слагаемом добавляется множитель q. Поэтому 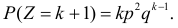
Ответ. 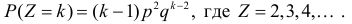
Пример №3
Случайные X и Y независимы, причем X равномерно распределена на отрезке [0;2], а Y имеет функцию распределения 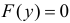 при
при 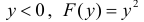 при
при 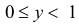 и
и 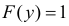 при
при 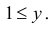 Требуется найти дисперсию произведения этих величин.
Требуется найти дисперсию произведения этих величин.
Решение. По свойству дисперсий для независимых случайных величин Х и Y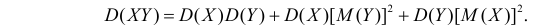
Вычислим величины из правой части этого равенства. Так как все значения X равновозможны в отрезке [0;2], то 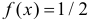 при
при 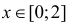 и
и 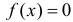 при остальных
при остальных 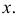 Поэтому
Поэтому
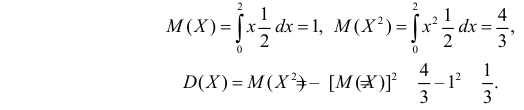
Случайная величина Y имеет функцию плотности вероятности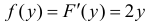 при
при 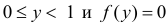 при остальных
при остальных 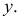 Поэтому
Поэтому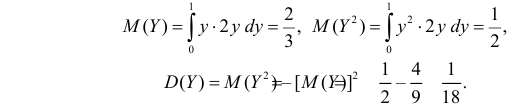
В итоге 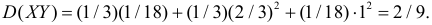
Ответ. 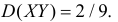
Распределение системы двух дискретных случайных величин
Распределение системы двух дискретных случайных 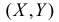 величин можно задать в виде таблицы, в которой перечислены пары возможных значений
величин можно задать в виде таблицы, в которой перечислены пары возможных значений 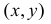 и их вероятности:
и их вероятности:
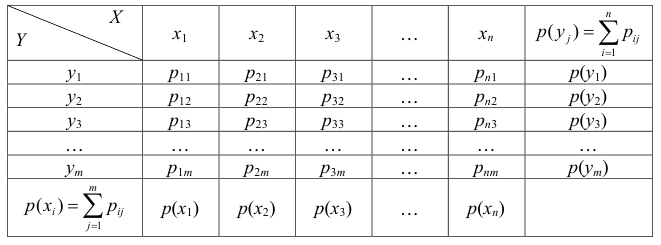
В этой таблице 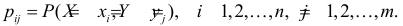 При этом
При этом 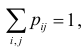
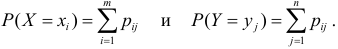 Если X и Y независимы, то
Если X и Y независимы, то 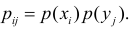
Пример №4
Закон распределения дискретного случайного вектора задан в виде таблицы:
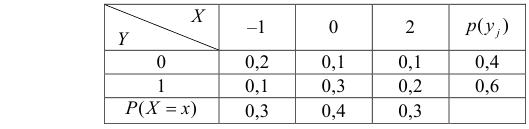
Требуется найти распределение случайных величин 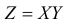 и
и 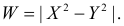
Решение. Найдем возможные значения случайной величины 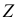 :
: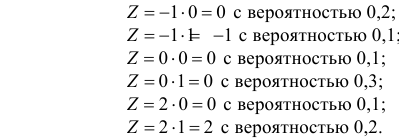
Закон распределения случайной величины 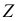 запишем в виде ряда распределения
запишем в виде ряда распределения

Случайная величина 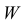 принимает значения:
принимает значения:
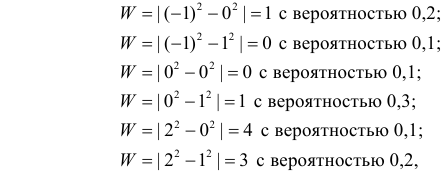
и имеет ряд распределения

Ответ. 

Распределение функции двух случайных величин
Рассмотрим функцию двух случайных величин 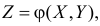 где
где 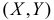 – система двух случайных величин (случайный вектор в плоскости). Пусть случайная точка
– система двух случайных величин (случайный вектор в плоскости). Пусть случайная точка 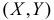 имеет функцию плотности вероятности
имеет функцию плотности вероятности 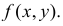 Найдем функцию распределения
Найдем функцию распределения 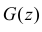 случайной величины
случайной величины 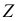 .
.
Для каждого 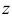 обозначим через
обозначим через 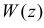 область на плоскости, в которой выполняется неравенство
область на плоскости, в которой выполняется неравенство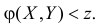 Чтобы это неравенство выполнилось, случайная точка должна попасть в область
Чтобы это неравенство выполнилось, случайная точка должна попасть в область 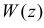 . По определению
. По определению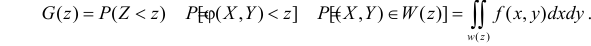
Тогда плотность распределения случайной величины 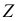 равна
равна 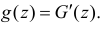
Пример №5
В квадрат со стороной a наугад брошена точка. Пусть Y – расстояние от этой точки до ближайшей стороны квадрата. Считая все положения точки в квадрате равновозможными, найдите функцию плотности вероятности величины 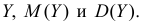
Решение. Пусть Y – расстояние от точки до ближайшей стороны квадрата. Для определенности будем считать, что точка попала в треугольник AOD (см. рис. 2.12.5).
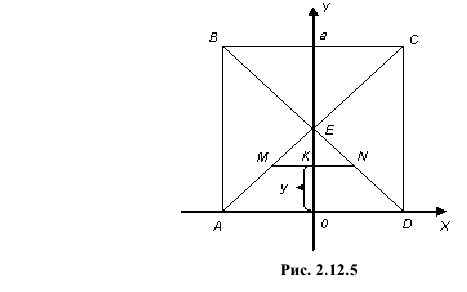
Для всех точек этого треугольника AD – ближайшая сторона квадрата. Так как площадь треугольника AOD равна 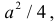 то плотность вероятности случайной точки в этом треугольнике
то плотность вероятности случайной точки в этом треугольнике 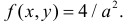 Вне треугольника
Вне треугольника 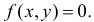 Расстояние от точки до основания будет равно
Расстояние от точки до основания будет равно 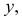 если точка упадет на отрезок MN. Поскольку
если точка упадет на отрезок MN. Поскольку 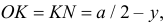 то плотность вероятности случайной величины Y получим, если проинтегрируем плотность вероятности
то плотность вероятности случайной величины Y получим, если проинтегрируем плотность вероятности 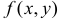 в пределах от
в пределах от 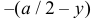 до
до 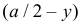 (т.е. от точки M до точки N):
(т.е. от точки M до точки N):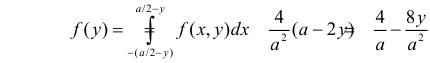 при
при 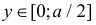
и 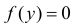 при остальных
при остальных 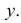 Поэтому
Поэтому 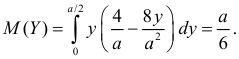 Для вычисления дисперсии найдем сначала
Для вычисления дисперсии найдем сначала 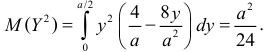
Откуда 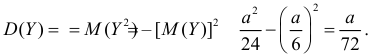
Ответ. 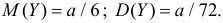
Пример №6
Две вершины треугольника совпадают с концами диаметра круга радиуса R, а третья вершина располагается в случайной точке 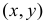 в верхней половине круга. Полагая равновозможными все положения третьей вершины в верхней половине круга, найдите функцию плотности вероятности для площади треугольника и математическое ожидание этой площади.
в верхней половине круга. Полагая равновозможными все положения третьей вершины в верхней половине круга, найдите функцию плотности вероятности для площади треугольника и математическое ожидание этой площади.
Решение. Так как все положения точки 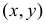 в полукруге равновозможны, а площадь полукруга равна
в полукруге равновозможны, а площадь полукруга равна 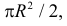 то плотность вероятности случайной точки
то плотность вероятности случайной точки 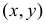 имеет вид:
имеет вид: 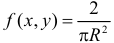 во всех точках полукруга, и
во всех точках полукруга, и 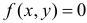 вне полукруга. Основание треугольника постоянно и равно
вне полукруга. Основание треугольника постоянно и равно 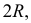 а высота треугольника равна ординате случайной точки
а высота треугольника равна ординате случайной точки 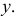 Поэтому площадь треугольника равна
Поэтому площадь треугольника равна 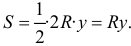 Высота треугольника будет равна
Высота треугольника будет равна 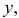 если случайная точка упадет на отрезок
если случайная точка упадет на отрезок 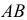 (см. рис. 2.12.6). Для получения плотности вероятности в точке y необходимо просуммировать плотность вероятности
(см. рис. 2.12.6). Для получения плотности вероятности в точке y необходимо просуммировать плотность вероятности 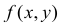 вдоль отрезка
вдоль отрезка 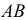 :
: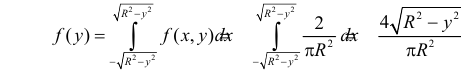 при
при 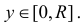
В итоге среднее значение площади треугольника равно 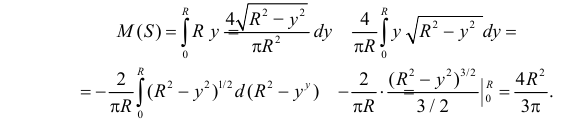
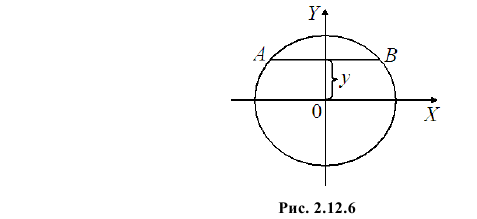
Ответ. 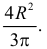
Пример №7
Все положения случайной точки 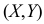 равновозможны в квадрате со стороной, равной единице. Найдите функцию плотности вероятности случайной величины
равновозможны в квадрате со стороной, равной единице. Найдите функцию плотности вероятности случайной величины 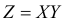 и ее среднее значение.
и ее среднее значение.
Решение. Так как все положения случайной точки 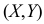 равновозможны в квадрате со стороной, равной единице, то эта случайная точка имеет функцию плотности вероятности
равновозможны в квадрате со стороной, равной единице, то эта случайная точка имеет функцию плотности вероятности 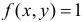 внутри квадрата и
внутри квадрата и 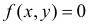 вне квадрата.
вне квадрата.
Найдем сначала функцию распределения случайной величины 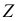 . По определению
. По определению 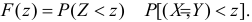 Неравенство
Неравенство 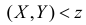 выполняется, если случайная точка
выполняется, если случайная точка 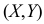 окажется внутри квадрата ниже гиперболы
окажется внутри квадрата ниже гиперболы 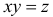 (см. рис. 2.12.7). Поэтому
(см. рис. 2.12.7). Поэтому
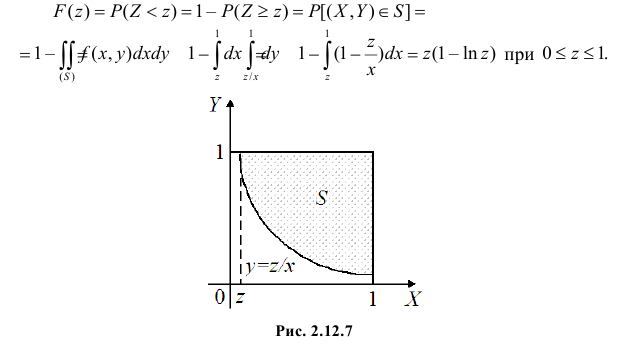
Окончательно можно записать: 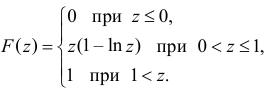
Дифференцируя 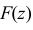 по
по 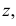 получаем функцию плотности вероятности
получаем функцию плотности вероятности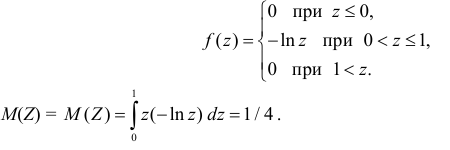
Ответ. 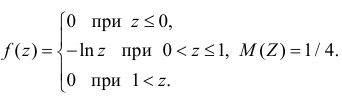
Замечание. Если требуется найти лишь математическое ожидание случайной величины 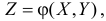 то нет необходимости предварительно находить закон распределения
то нет необходимости предварительно находить закон распределения 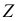 . Если известна, например,
. Если известна, например, 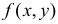 – функция плотности вероятности случайной точки
– функция плотности вероятности случайной точки 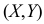 , то среднее значение
, то среднее значение 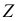 можно вычислить непосредственно по формуле:
можно вычислить непосредственно по формуле:
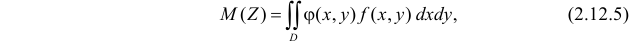
где D – область возможных значений двумерной случайной величины 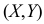 .
.
Пример 2.75. Все положения случайной точки 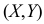 в области
в области 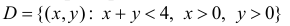 равновозможны. Величина X равна стороне основания правильной четырехугольной пирамиды, а Y равняется высоте этой пирамиды. Найдите математическое ожидание объема пирамиды.
равновозможны. Величина X равна стороне основания правильной четырехугольной пирамиды, а Y равняется высоте этой пирамиды. Найдите математическое ожидание объема пирамиды.
Решение. Область D представляет из себя треугольник, площадь которого равна восьми. Так как все положения случайной точки 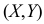 в треугольнике равновозможны, то функция плотности вероятности
в треугольнике равновозможны, то функция плотности вероятности 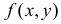 внутри этого треугольника постоянна. Поэтому
внутри этого треугольника постоянна. Поэтому 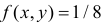 во внутренних точках треугольника и
во внутренних точках треугольника и 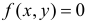 вне треугольника (см. рис. 2.12.8).
вне треугольника (см. рис. 2.12.8).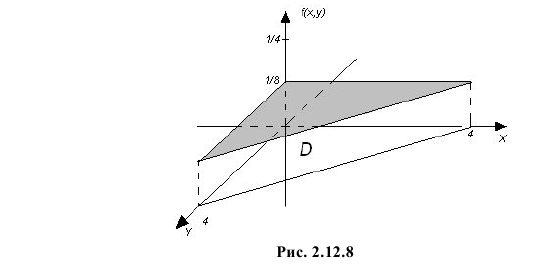
Объем пирамиды равен 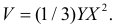 Поэтому по формуле (2.12.5) имеем
Поэтому по формуле (2.12.5) имеем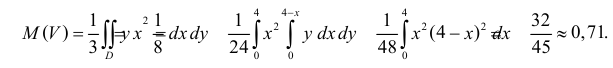
Ответ. 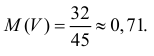
Пример №8
Равновозможны все положения случайной точки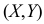 в круге радиуса R с центром в начале координат (иначе говоря, случайный вектор
в круге радиуса R с центром в начале координат (иначе говоря, случайный вектор 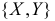 распределен равномерно в указанном круге). Требуется найти плотность вероятности случайной величины
распределен равномерно в указанном круге). Требуется найти плотность вероятности случайной величины 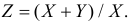
Решение. Так как все положения случайной точке в круге равновозможны, а площадь круга равна 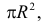 то плотность вероятности случайной точки
то плотность вероятности случайной точки 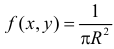 внутри круга и
внутри круга и 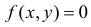 вне круга. Найдем сначала функцию распределения случайной величины
вне круга. Найдем сначала функцию распределения случайной величины 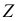 . По определению
. По определению 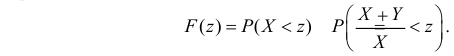
Неравенство 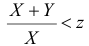 при
при 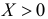 преобразуется к виду
преобразуется к виду 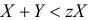 или
или 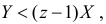 а при
а при 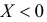 получаем
получаем 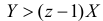 . Это означает, что, неравенство выполняется в заштрихованной на рис. 2.12.9 и рис. 2.12.10 области .
. Это означает, что, неравенство выполняется в заштрихованной на рис. 2.12.9 и рис. 2.12.10 области .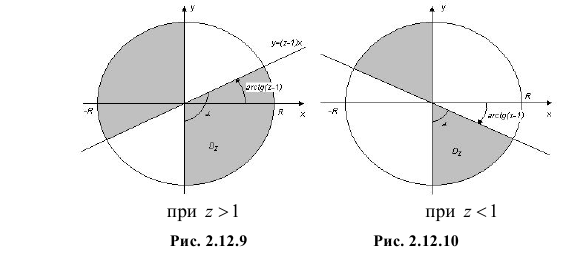
Поэтому
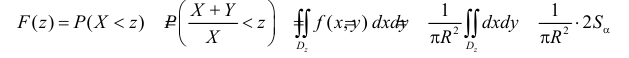
где 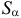 – площадь кругового сектора с углом a.
– площадь кругового сектора с углом a.
Заметим, что тангенс угла наклона прямой 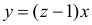 равен
равен 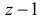 . Поэтому при
. Поэтому при 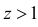 угол
угол 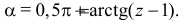 При
При 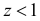 тоже
тоже 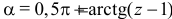 , так как в этом случае
, так как в этом случае 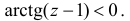 Поэтому площадь сектора
Поэтому площадь сектора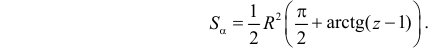
Итак,
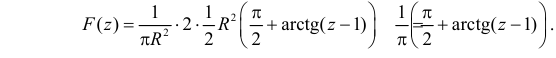
В итоге получаем
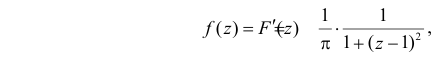
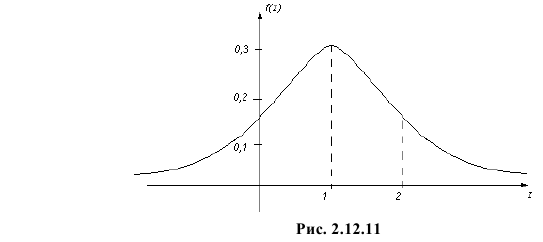
т.е. стандартный закон распределения Коши, только сдвинутый на единицу вправо (см. рис. 2.12.11).
Ответ. 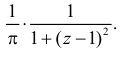
Пример №9
Время безотказной работы каждого элемента имеет показательный закон распределения 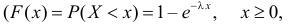
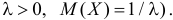 Cчитая, что элементы выходят из строя независимо друг от друга, найти среднее время безотказной работы («наработку на отказ») для каждой из систем:
Cчитая, что элементы выходят из строя независимо друг от друга, найти среднее время безотказной работы («наработку на отказ») для каждой из систем:
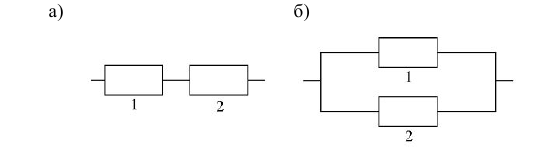
Решение. Обозначим время безотказной работы 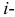 го элемента через
го элемента через 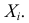 Система а) выходит из строя вместе с первым отказавшим элементом, поэтому время безотказной работы первой системы
Система а) выходит из строя вместе с первым отказавшим элементом, поэтому время безотказной работы первой системы 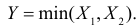 Заметим, что
Заметим, что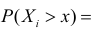
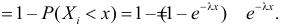 Найдем функцию распределения величины Y:
Найдем функцию распределения величины Y: 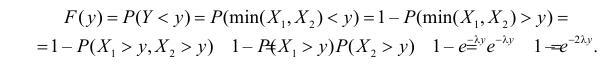
Оказалось, что величина 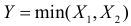 имеет показательный закон распределения с параметром
имеет показательный закон распределения с параметром 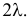 Наработка на отказ для системы с последовательным соединением элементов равна
Наработка на отказ для системы с последовательным соединением элементов равна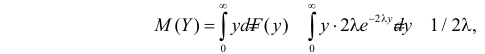
т.е. в два раза меньше наработки на отказ одного элемента.
Система б) работает безотказно, пока в рабочем состоянии находится хотя бы один из двух элементов. Поэтому ее время безотказной работы 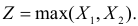 Найдем функцию распределения величины
Найдем функцию распределения величины 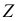 :
: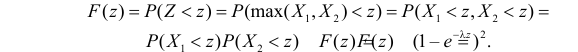
Наработка на отказ для системы с параллельным соединением элементов (такое соединение при одновременно работающих элементах называют нагруженным или «горячим» резервированием) равна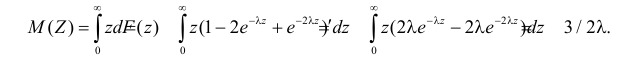
Ответ. 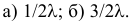
Пример №10
Пусть 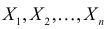 – последовательность независимых случайных величин, каждая из которых имеет равномерное распределение в интервале (0,1). Пусть
– последовательность независимых случайных величин, каждая из которых имеет равномерное распределение в интервале (0,1). Пусть 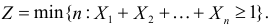 Требуется найти
Требуется найти 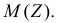
Решение. По условию каждая из случайных величин равномерно распределена в интервале (0,1), т.е. имеет функцию распределения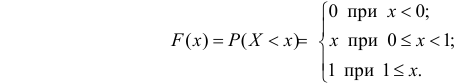
Соответствующая функция плотности вероятности 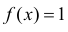 при
при 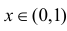 и
и 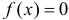 при остальных
при остальных 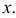 Понятно, что
Понятно, что 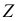 принимает значения 2, 3, 4, … . Поэтому
принимает значения 2, 3, 4, … . Поэтому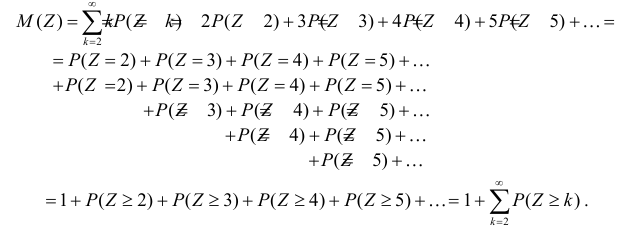
Введем обозначение 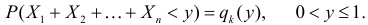 Заметим, что
Заметим, что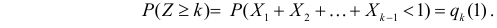
Легко видеть, что 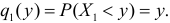 Тогда полная вероятность того, что
Тогда полная вероятность того, что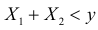 равна
равна 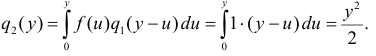 Тогда
Тогда 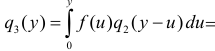
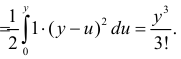 Продолжая рассуждать подобным образом, получим рекуррентное соотношение для величин
Продолжая рассуждать подобным образом, получим рекуррентное соотношение для величин 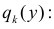
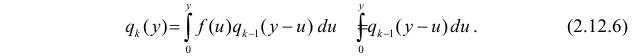
По формуле (2.12.6) 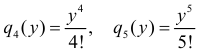 и т.д. По методу математической индукции предполагаем, что
и т.д. По методу математической индукции предполагаем, что 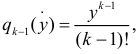 откуда
откуда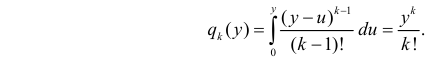
В итоге получаем, что
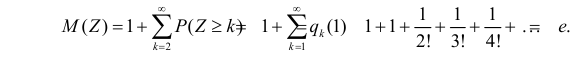
Ответ. 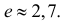
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Центральная предельная теорема
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности
- Числовые характеристики случайных величин
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний