
Функции многих переменных - определение и вычисление с примерами решения
Содержание:
Функции многих переменных
Будем рассматривать несколько переменных величин: 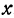
Определение. Если каждой возможной совокупности числовых значений переменных 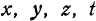 .. . соответствуют определенные значения переменного w, то w называется зависимым переменным, или функцией от независимых переменных
.. . соответствуют определенные значения переменного w, то w называется зависимым переменным, или функцией от независимых переменных 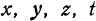 , .... или функцией многих переменных. Функция многих переменных обозначается так:
, .... или функцией многих переменных. Функция многих переменных обозначается так: 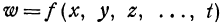 .
.
Приведем примеры функций двух и трех переменных.
Пример:
Площадь 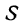 прямоугольного треугольника выражается через его катеты
прямоугольного треугольника выражается через его катеты 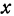 и
и 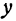 формулой
формулой 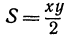 . Поэтому площадь
. Поэтому площадь 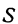 есть функция двух независимых переменных.
есть функция двух независимых переменных.
Пример:
По закону Ома 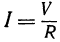 , где
, где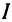 — ток,
— ток, 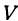 — напряжение, a
— напряжение, a 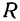 —сопротивление. Значит, ток
—сопротивление. Значит, ток 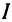 есть функция двух переменных:
есть функция двух переменных: 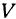 и
и 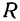 .
.
Пример:
Сила 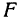 равна произведению массы на ускорение:
равна произведению массы на ускорение: 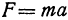 . Здесь опять сила есть функция двух переменных:
. Здесь опять сила есть функция двух переменных: 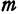 и
и 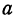 .
.
Пример:
Как известно, площадь косоугольного треугольника выражается через две его стороны и угол между ними следующим образом:
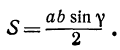
Поэтому площадь треугольника является функцией трех независимых переменных: 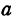 ,
, 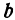 и
и 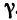 .
.
Может случиться, что уравнение, которое связывает переменные величины, не разрешено относительно ни одной из них, тем не менее оно определяет функцию или функции. Например, уравнение 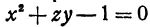 определяет функцию
определяет функцию 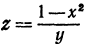 . Уравнение
. Уравнение 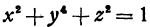 определяет функции
определяет функции 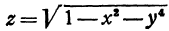 и
и 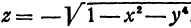 .
.
Определение. Функция, заданная уравнением, не разрешенным относительно этой функции, называется неявной.
Иногда удается представить неявную функцию в явном виде. Например, если дана неявная функция, определенная уравнением 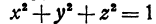 , то, решая уравнение, получим две явные функции:
, то, решая уравнение, получим две явные функции:
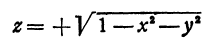
и 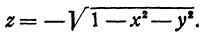
Совокупность всех значений независимых переменных, для которых можно найти значения функции, называется областью существования функции. Например, если задана функция 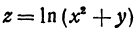 , то область ее существования будет состоять из значений
, то область ее существования будет состоять из значений 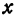 и
и 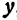 , удовлетворяющих неравенству
, удовлетворяющих неравенству 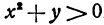 .
.
Координаты в пространстве
Для того чтобы иметь возможность дать геометрическое истолкование функции двух переменных, введем в пространстве систему координат. Возьмем три взаимно перпендикулярные и пересекающиеся в одной точке прямые и на каждой из них:
- установим направление,
- выберем единицу масштаба,
- укажем начало отсчета.
Обычно масштаб берется одинаковый по всем трем прямым, а за начало отсчета принимается точка пересечения данных прямых.
Совокупность трех взаимно перпендикулярных пересекающихся в одной точке прямых, на которых: 1) установлено направление, 2) введен масштаб и 3) выбрано начало отсчета, называется системой координат.
Каждую из этих прямых называют осью координат, одну из них—осью абсцисс или осью 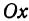 , другую—осью ординат или осью
, другую—осью ординат или осью 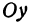 и третью — осью аппликат или осью
и третью — осью аппликат или осью 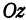 . Точку начала отсчета, общую для координат и обозначают буквой
. Точку начала отсчета, общую для координат и обозначают буквой 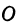 . Положительное направление осей указано на рис. 99.
. Положительное направление осей указано на рис. 99.
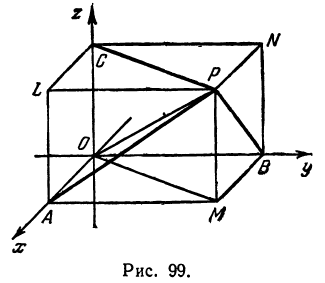
Пусть 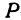 —произвольная точка пространства. Опустим из нее перпендикуляры на оси координат и назовем проекцию точки на ось
—произвольная точка пространства. Опустим из нее перпендикуляры на оси координат и назовем проекцию точки на ось  буквой
буквой  , на ось
, на ось 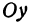 —буквой
—буквой 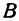 и на ось
и на ось 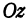 —буквой
—буквой 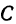 (рис. 99).
(рис. 99).
Отрезки 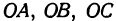 назовем координатными отрезками точки
назовем координатными отрезками точки 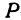 (ср. с гл. 1). Определение координат точки остается таким же, как и в гл. 1, только добавляется, что координата, измеряемая по оси
(ср. с гл. 1). Определение координат точки остается таким же, как и в гл. 1, только добавляется, что координата, измеряемая по оси 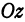 , называется аппликатой. Точка
, называется аппликатой. Точка 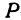 , имеющая абсциссой число
, имеющая абсциссой число 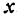 , ординатой число
, ординатой число 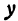 и аппликатой число
и аппликатой число 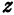 , записывается так:
, записывается так: 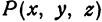 .
.
Точки 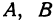 и
и 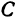 можно получить и другим способом. Покажем это для точки
можно получить и другим способом. Покажем это для точки 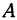 (рис. 99). Спроектируем точку
(рис. 99). Спроектируем точку 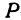 на плоскость
на плоскость 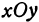 , т. е. опустим из нее перпендикуляр на эту плоскость; получим точку
, т. е. опустим из нее перпендикуляр на эту плоскость; получим точку 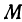 . Теперь опустим перпендикуляр из
. Теперь опустим перпендикуляр из 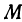 на ось
на ось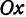 . Основанием перпендикуляра на ось
. Основанием перпендикуляра на ось 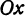 как раз и будет точка
как раз и будет точка 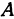 (это следует из теоремы о трех перпендикулярах). Часто при изображении точки
(это следует из теоремы о трех перпендикулярах). Часто при изображении точки 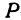 для наглядности, наряду с осями координат, изображают прямоугольный параллелепипед. Одна из вершин параллелепипеда находится в заданной точке
для наглядности, наряду с осями координат, изображают прямоугольный параллелепипед. Одна из вершин параллелепипеда находится в заданной точке 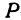 , а противоположная—в начале координат
, а противоположная—в начале координат  ; три его ребра расположены по осям координат. На рис. 99 это параллелепипед
; три его ребра расположены по осям координат. На рис. 99 это параллелепипед 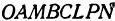 . Тогда становится очевидным, что
. Тогда становится очевидным, что 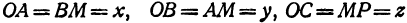 и что
и что 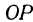 —диагональ параллелепипеда. Так как
—диагональ параллелепипеда. Так как 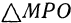 и
и 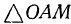 прямоугольные, то
прямоугольные, то 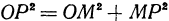 и
и 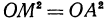
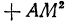 , откуда
, откуда 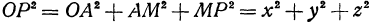 и
и 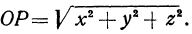
Таким образом, расстояние точки от начала координат равно квадратному корню из суммы квадратов ее координат.
Пример:
Найти расстояние между точками 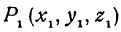 и
и 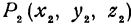 .
.
Решение:
Обозначим проекции точек 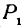 , и
, и 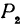 на ось
на ось 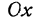 соответственно через
соответственно через 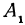 и
и 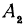 (рис. 100).
(рис. 100).
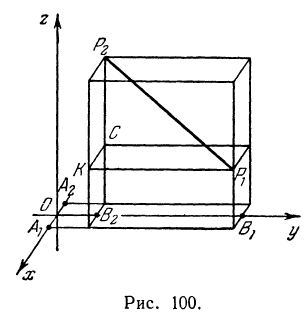
Тогда проекцией отрезка 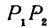 будет являться отрезок
будет являться отрезок 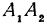 . Выразим отрезок
. Выразим отрезок 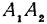 через координаты начала и конца, он равен координате конца минус координата начала, т. е.
через координаты начала и конца, он равен координате конца минус координата начала, т. е. 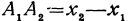 , а его длина равна
, а его длина равна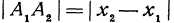 (см. гл. I). Кроме того, в силу равенства отрезков параллельных прямых, заключенных между параллельными плоскостями, имеем:
(см. гл. I). Кроме того, в силу равенства отрезков параллельных прямых, заключенных между параллельными плоскостями, имеем: 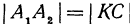 . Аналогично, проектируя точки
. Аналогично, проектируя точки 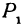 и
и 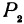 на ось
на ось 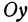 , получим, что
, получим, что 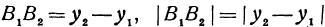 и
и 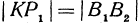 . Также получаем, что
. Также получаем, что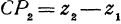 и
и 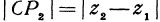 . Диагональ
. Диагональ 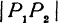 прямоугольного параллелепипеда равна
прямоугольного параллелепипеда равна
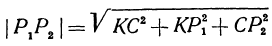
или
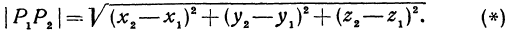
Следовательно, расстояние между двумя точками равно квадратному корню из суммы квадратов разностей соответствующих координат.
Некоторые простые уравнения
1. Уравнения координатных плоскостей. Рассмотрим, например, плоскость 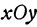 и произвольную точку
и произвольную точку 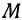 на ней.
на ней.
Так как плоскость 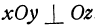 , то перпендикуляр, опущенный из точки
, то перпендикуляр, опущенный из точки 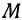 на ось
на ось 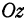 , попадает в начало координат, а это значит, что аппликата точки равна нулю. Очевидно и обратное, т. е. если аппликата точки равна нулю, то эта точка лежит в плоскости
, попадает в начало координат, а это значит, что аппликата точки равна нулю. Очевидно и обратное, т. е. если аппликата точки равна нулю, то эта точка лежит в плоскости  . Поэтому уравнение
. Поэтому уравнение 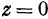 характеризует плоскость
характеризует плоскость 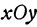 ; оно является уравнением плоскости
; оно является уравнением плоскости 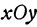 , т. е. координаты любой точки плоскости
, т. е. координаты любой точки плоскости 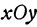 удовлетворяют уравнению
удовлетворяют уравнению 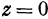 .
.
Рассуждая аналогично, получим, что координаты любой точки, принадлежащей плоскости 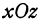 , удовлетворяют уравнению
, удовлетворяют уравнению 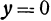 , т. е. это уравнение есть уравнение координатной плоскости
, т. е. это уравнение есть уравнение координатной плоскости 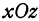 . Также уравнение
. Также уравнение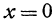 есть уравнение координатной плоскости
есть уравнение координатной плоскости 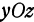 .
.
2. Уравнение плоскости, параллельной координатной плоскости. Если точка 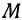 лежит в плоскости, параллельной плоскости
лежит в плоскости, параллельной плоскости 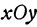 , то ее аппликата равна расстоянию точки от плоскости
, то ее аппликата равна расстоянию точки от плоскости 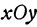 , взятому со знаком плюс, если точка лежит выше, и со знаком минус, если она лежит ниже координатной плоскости
, взятому со знаком плюс, если точка лежит выше, и со знаком минус, если она лежит ниже координатной плоскости 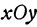 . Поэтому уравнение плоскости, параллельной координатной плоскости
. Поэтому уравнение плоскости, параллельной координатной плоскости 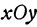 , имеет вид
, имеет вид 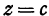 , где
, где 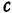 — постоянное.
— постоянное.
Также плоскость, параллельная плоскости 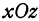 , имеет уравнение
, имеет уравнение 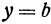 . Плоскость, параллельная плоскости
. Плоскость, параллельная плоскости 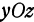 , имеет уравнение
, имеет уравнение  .
.
3. Уравнения координатных осей. Ось 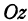 является пересечением плоскости
является пересечением плоскости 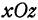 и плоскости
и плоскости 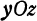 , поэтому любая ее точка лежит в плоскости
, поэтому любая ее точка лежит в плоскости 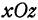 и в плоскости
и в плоскости 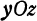 . Следовательно, координаты любой точки, принадлежащей оси
. Следовательно, координаты любой точки, принадлежащей оси 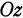 , должны удовлетворять и уравнению
, должны удовлетворять и уравнению 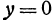 и уравнению
и уравнению 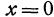 . Эти два уравнения
. Эти два уравнения 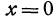 и
и 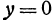 являются уравнениями оси
являются уравнениями оси 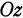 . Аналогично уравнениями оси
. Аналогично уравнениями оси 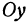 будут
будут 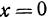 ,
,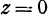 . Уравнениями оси
. Уравнениями оси 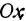 ; будут
; будут 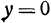 ,
, 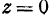 .
.
Поверхности
Пусть дана функция двух независимых переменных, определенная уравнением

Будем рассматривать переменные 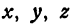 как координаты точки. Возьмем на плоскости
как координаты точки. Возьмем на плоскости 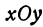 точку
точку 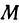 , т. е. укажем пару чисел
, т. е. укажем пару чисел 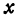 и
и 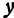 (ее координаты). В силу уравнения (1) паре чисел
(ее координаты). В силу уравнения (1) паре чисел 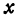 и
и 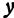 соответствует определенное число
соответствует определенное число 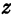 . Поэтому можно сказать, что уравнение (1) ставит в соответствие точке
. Поэтому можно сказать, что уравнение (1) ставит в соответствие точке 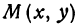 , лежащей на плоскости
, лежащей на плоскости 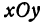 , точку
, точку 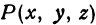 , лежащую в пространстве. Меняя положение точки
, лежащую в пространстве. Меняя положение точки 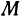 на плоскости
на плоскости 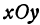 , будем получать различные точки
, будем получать различные точки 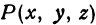 . Геометрическое место точек
. Геометрическое место точек 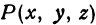 , координаты которых удовлетворяют уравнению (1), называется поверхностью. Для примера возьмем формулу, выражающую расстояние между двумя точками (формула
, координаты которых удовлетворяют уравнению (1), называется поверхностью. Для примера возьмем формулу, выражающую расстояние между двумя точками (формула 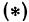 из § 2):
из § 2):
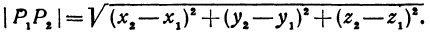
Предположим, что точка 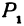 неподвижна, расстояние между точками
неподвижна, расстояние между точками 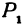 и
и 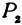 постоянно и равно
постоянно и равно 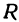 , а точка
, а точка 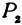 может двигаться. Тогда геометрическое место точек
может двигаться. Тогда геометрическое место точек 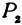 будет являться поверхностью шара, или, как иначе говорят, сферой. Обозначим координаты точки
будет являться поверхностью шара, или, как иначе говорят, сферой. Обозначим координаты точки 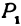 через
через 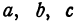 , а координаты
, а координаты 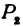 через
через 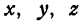 (здесь
(здесь 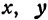 и
и 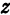 являются переменными величинами). Тогда равенство
являются переменными величинами). Тогда равенство 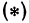 перепишется в виде
перепишется в виде
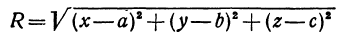
или
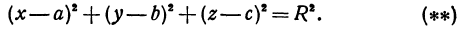
Это—неявная функция. Координаты, удовлетворяющие уравнению 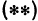 , определяют точки, лежащие на сфере. Поэтому уравнение
, определяют точки, лежащие на сфере. Поэтому уравнение 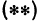 называют уравнением сферы, имеющей центр в точке
называют уравнением сферы, имеющей центр в точке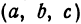 и радиус, равный
и радиус, равный 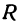 . Таким образом, уравнение (1) определяет поверхность и называется уравнением поверхности.
. Таким образом, уравнение (1) определяет поверхность и называется уравнением поверхности.
Для того чтобы выяснить вид поверхности, определенной уравнением (1), применяют метод сечений, с которым мы познакомимся на примерах.
Пример:
Выясним вид поверхности, заданной уравнением
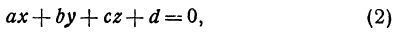
иначе говоря, найдем геометрический смысл неявной функции, определенной уравнением (2).
Решение:
Для этого найдем сначала точки пересечения поверхности с осью  . Поскольку для любой точки, лежащей на оси
. Поскольку для любой точки, лежащей на оси  , абсцисса и ордината равны нулю, то искомая точка удовлетворяет этим условиям и уравнению (2). Подставляя в уравнение (2)
, абсцисса и ордината равны нулю, то искомая точка удовлетворяет этим условиям и уравнению (2). Подставляя в уравнение (2) 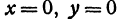 , найдем
, найдем 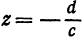 . Таким образом, точка
. Таким образом, точка 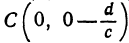 есть точка пересечения поверхности, заданной уравнением (2), с осью
есть точка пересечения поверхности, заданной уравнением (2), с осью 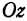 . Чтобы найти точку пересечения поверхности с осью
. Чтобы найти точку пересечения поверхности с осью 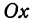 , положим в уравнении (2)
, положим в уравнении (2) 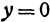 и
и 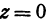 . Отсюда найдем
. Отсюда найдем  . Итак, точка
. Итак, точка 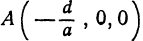 есть точка пересечения поверхности с осью
есть точка пересечения поверхности с осью 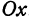 .
.
Аналогично, полагая в уравнении (2) 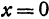 и
и 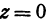 , получим, что точка
, получим, что точка 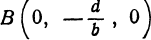 является точкой пересечения поверхности (2) с осью
является точкой пересечения поверхности (2) с осью  (рис. 101).
(рис. 101).
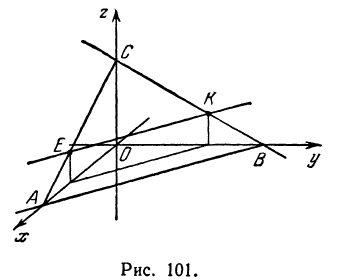
Выясним, что получится при пересечении поверхности (2) с плоскостью  . Так как уравнение этой плоскости
. Так как уравнение этой плоскости  , то, полагая в уравнении (2)
, то, полагая в уравнении (2) 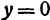 , получим
, получим 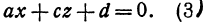
Как было показано в гл. II, всякое уравнение первой степени с двумя неизвестными определяет некоторую прямую на плоскости, поэтому уравнение (3) определяет прямую, лежащую в плоскости 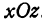 . Прямая, определенная уравнением (3), проходит через точки
. Прямая, определенная уравнением (3), проходит через точки 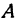 и
и 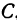 , так как их координаты удовлетворяют уравнению (3). Проверим это для точки
, так как их координаты удовлетворяют уравнению (3). Проверим это для точки 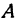 :
:
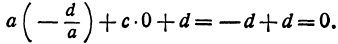
Полагая в уравнении (2) 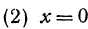 , найдем пересечение поверхности с координатной плоскостью
, найдем пересечение поверхности с координатной плоскостью 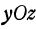 . Снова получим прямую, определяемую уравнением
. Снова получим прямую, определяемую уравнением

проходящую через точки 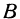 и
и  .
.
Наконец, пересекая поверхность (2) плоскостью 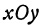 , т. е. полагая в уравнении (2)
, т. е. полагая в уравнении (2) 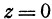 , получим
, получим

Уравнение (5) определяет прямую, лежащую в плоскости 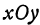 и проходящую через точки
и проходящую через точки 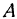 и
и 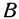 .
.
Итак, поверхность, заданная уравнением (2), пересекается с координатными плоскостями по треугольнику 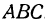 .
.
Чтобы выяснить окончательно вид поверхности, пересечем ее плоскостью, параллельной плоскости 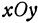 , которая имеет уравнение
, которая имеет уравнение 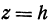 . Полагая в уравнении (2)
. Полагая в уравнении (2) 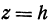 , получим
, получим
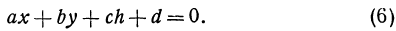
Это — уравнение прямой, лежащей в плоскости 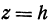 . Найдем точку пересечения прямой (6) с плоскостью
. Найдем точку пересечения прямой (6) с плоскостью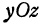 , для этого положим в уравнении (6)
, для этого положим в уравнении (6) 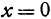 , тогда
, тогда 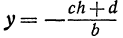 • Найденная точка
• Найденная точка 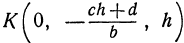 , лежит и на прямой
, лежит и на прямой 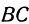 , поскольку ее ордината
, поскольку ее ордината 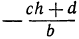 и аппликата
и аппликата 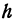 удовлетворяют уравнению (4). Также, если в уравнении (6) положить
удовлетворяют уравнению (4). Также, если в уравнении (6) положить 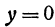 , то найдем точку пересечения прямой (6) с координатной плоскостью
, то найдем точку пересечения прямой (6) с координатной плоскостью 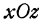 , это будет точка £
, это будет точка £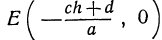 .
.
Точка 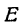 лежит и на прямой
лежит и на прямой 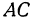 , так как ее координаты удовлетворяют уравнению (3).
, так как ее координаты удовлетворяют уравнению (3).
Число 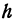 можно менять, поэтому в результате проведенного исследования получается, что поверхность, определяемая уравнением (2), образована прямой
можно менять, поэтому в результате проведенного исследования получается, что поверхность, определяемая уравнением (2), образована прямой 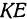 , скользящей по пересекающимся прямым
, скользящей по пересекающимся прямым 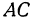 и
и 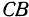 . Эта поверхность является плоскостью.
. Эта поверхность является плоскостью.
Итак, уравнение первой степени с тремя неизвестными в пространстве определяет плоскость.
Пример:
Найдем вид поверхности, определяемой уравнением

Решение:
Пересечем поверхность плоскостью 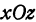 , т. е. положим в уравнении (7)
, т. е. положим в уравнении (7) 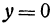 . Получим
. Получим 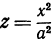 это — уравнение параболы, лежащей в координатной плоскости
это — уравнение параболы, лежащей в координатной плоскости 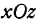 (рис. 102).
(рис. 102).
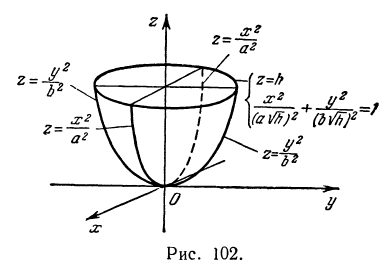
Пересекая поверхность плоскостью 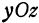 , т. е. полагая в уравнении (7)
, т. е. полагая в уравнении (7)  , получим уравнение
, получим уравнение 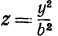 , которое является также уравнением параболы.
, которое является также уравнением параболы.
Найдем пересечение исследуемой поверхности с плоскостью 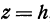 , т. е. с плоскостью, параллельной плоскости
, т. е. с плоскостью, параллельной плоскости 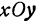 и отстоящей от нее на расстояние
и отстоящей от нее на расстояние 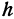 . Полагая
. Полагая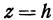 в уравнении (7), получим
в уравнении (7), получим 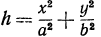 или
или
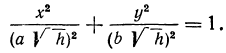
Это есть уравнение эллипса с полуосями 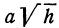 и
и 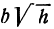 . Чем больше
. Чем больше 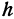 , тем больше и полуоси эллипса, следовательно, эллипс расширяется по мере удаления от координатной плоскости
, тем больше и полуоси эллипса, следовательно, эллипс расширяется по мере удаления от координатной плоскости 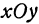 . При
. При  выражения для полуосей теряют смысл, так как корень квадратный делается мнимым. При
выражения для полуосей теряют смысл, так как корень квадратный делается мнимым. При 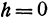 полуоси равны нулю.
полуоси равны нулю.
Поэтому исследуемая поверхность образована эллипсами, расположенными в плоскостях, параллельных плоскости 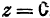 , и нанизанными на параболы
, и нанизанными на параболы 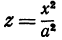 и
и 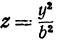 . Эта поверхность называется эллиптическим параболоидом.
. Эта поверхность называется эллиптическим параболоидом.
Пример:
Исследуем вид поверхности, заданной уравнением
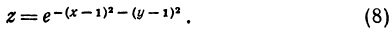
Решение:
Найдем пересечение с плоскостью 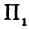 уравнение которой
уравнение которой 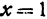 (рис. 103). Уравнение (8) после подстановки в него
(рис. 103). Уравнение (8) после подстановки в него 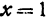 примет вид
примет вид

Эта кривая была исследована она лежит в плоскости, параллельной плоскости 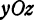 и отстоящей от нее на расстояние 1.
и отстоящей от нее на расстояние 1.
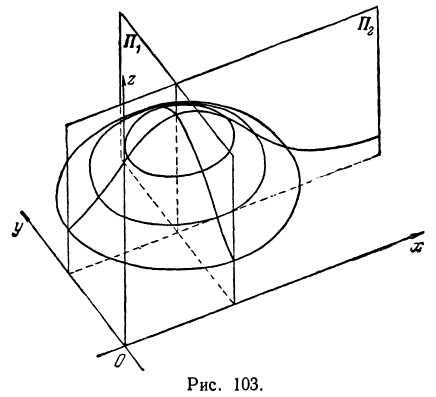
Пересекая поверхность (8) плоскостью 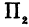 , уравнение которой
, уравнение которой 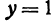 , получим уравнение кривой того же типа, что и (9):
, получим уравнение кривой того же типа, что и (9):

Ищем пересечение исследуемой поверхности с плоскостью, параллельной плоскости 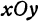 и отстоящей от нее на расстояние
и отстоящей от нее на расстояние 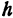 ; уравнение этой плоскости
; уравнение этой плоскости 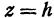 .
.
Подставляя 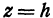 в уравнение (8), получаем
в уравнение (8), получаем
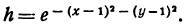
Прологарифмируем обе части последнего равенства и преобразуем; будем иметь:
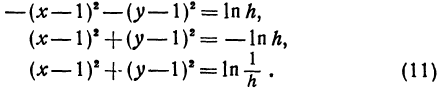
Это—уравнение окружности радиуса 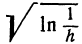 , центр которой находится в точке (1, 1,
, центр которой находится в точке (1, 1, 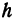 ). Чтобы радиус являлся действительным числом, под знаком квадратного корня должно стоять положительное число. А так как логарифмы положительны для чисел, больших единицы, то должно быть
). Чтобы радиус являлся действительным числом, под знаком квадратного корня должно стоять положительное число. А так как логарифмы положительны для чисел, больших единицы, то должно быть 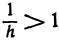 или
или  .
.
Это значит, что рассматриваемая поверхность пересекается с плоскостью 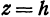 только в том случае, если
только в том случае, если 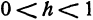 . Если
. Если 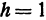 , то радиус обращается в нуль, т. е. окружность вырождается в точку. Итак, поверхность, определяемая уравнением (8), образована из окружностей (И), нанизанных на кривые (9) и (10). Окружности, образующие поверхность, увеличиваются по мере уменьшения
, то радиус обращается в нуль, т. е. окружность вырождается в точку. Итак, поверхность, определяемая уравнением (8), образована из окружностей (И), нанизанных на кривые (9) и (10). Окружности, образующие поверхность, увеличиваются по мере уменьшения 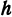 , т. е. по мере приближения к координатной плоскости
, т. е. по мере приближения к координатной плоскости 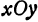 .
.
Линии уровня
Определение: Линией уровня называется геометрическое место точек, расположенных на поверхности и имеющих одну и ту же определенную аппликату.
Например, если дана поверхность 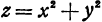 то, взяв
то, взяв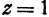 , получим
, получим 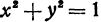 . Уравнение
. Уравнение 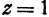 определяет плоскость, параллельную плоскости
определяет плоскость, параллельную плоскости 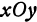 и отстоящую от нее на расстояние, равное единице. Уравнение
и отстоящую от нее на расстояние, равное единице. Уравнение 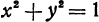 определяет окружность, лежащую в плоскости
определяет окружность, лежащую в плоскости 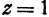 . Поэтому для рассматриваемой поверхности линией уровня, соответствующей уровню
. Поэтому для рассматриваемой поверхности линией уровня, соответствующей уровню 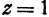 (аппликате
(аппликате 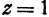 ), является окружность (рис. 104).
), является окружность (рис. 104).
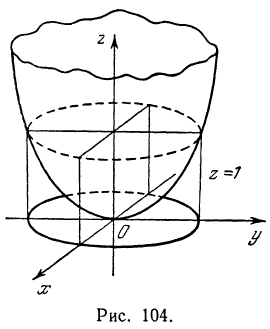
Ясно, что проекция линии уровня на плоскость 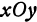 есть та же самая линия, только перенесенная параллельно самой себе в плоскость
есть та же самая линия, только перенесенная параллельно самой себе в плоскость 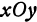 . Ее также называют линией уровня. В некоторых случаях линии уровня называют горизонталями.
. Ее также называют линией уровня. В некоторых случаях линии уровня называют горизонталями.
Часто прибегают к следующему приему изображения поверхностей: берут совокупность плоскостей, параллельных плоскости 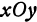 и отстоящих друг от друга на одно и то же расстояние. Находят пересечение каждой плоскости с поверхностью, т. е. линии уровня, изображают полученные линии на плоскости
и отстоящих друг от друга на одно и то же расстояние. Находят пересечение каждой плоскости с поверхностью, т. е. линии уровня, изображают полученные линии на плоскости 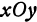 и таким образом получают карту поверхности (вернее, план поверхности). На этом плане по расположению горизонталей можно судить о рельефе поверхности.
и таким образом получают карту поверхности (вернее, план поверхности). На этом плане по расположению горизонталей можно судить о рельефе поверхности.
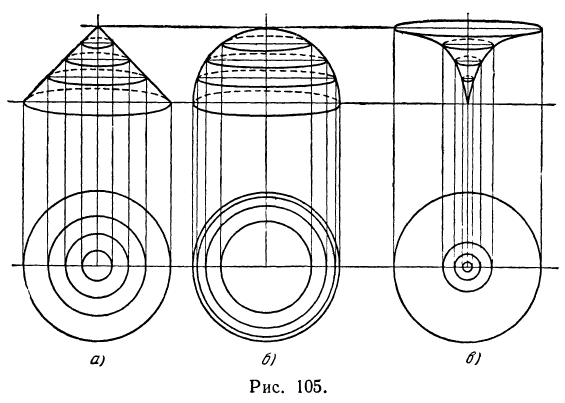
На рисунке 105 изображены три поверхности и под каждой из них нарисован ее план. Хотя число горизонталей (линий уровня) одно и то же для всех трех поверхностей, но расположение горизонталей различное. Можно заметить, что там, где поверхность круче, горизонтали расположены ближе друг к другу, или, как говорят, горизонтали расположены гуще.
Частные производные
В главе VIII было показано, как с помощью производной исследовать функцию. Для исследования функций многих переменных вводится понятие частной производной.
Определение: Частной производной от функции 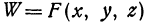 по переменному
по переменному 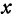 называется производная, вычисленная в предположении, что все независимые переменные, кроме
называется производная, вычисленная в предположении, что все независимые переменные, кроме 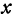 , сохраняют постоянное значение.
, сохраняют постоянное значение.
Частная производная по 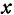 обозначается
обозначается 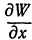 , или
, или 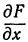 , или
, или 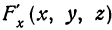 . Аналогично определяют и частные производные по другим независимым переменным:
. Аналогично определяют и частные производные по другим независимым переменным: 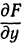 ,
, 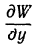 ,
, 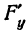 обозначают частную производную по
обозначают частную производную по 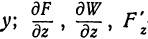 —частную производную по
—частную производную по 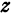 .
.
Пример:
Вычислим частные производные по всем независимым переменным от функции 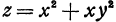 .
.
Решение:
Будем считать сначала 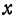 переменным, а
переменным, а 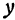 постоянным. Тогда, используя правила вычисления производных (см. гл. VII, § 4), получим
постоянным. Тогда, используя правила вычисления производных (см. гл. VII, § 4), получим
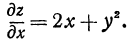
Аналогично
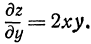
Пример:
Найдем частные производные функции 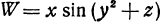 :
:
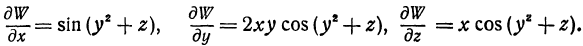
Определение: Частным приращением функции 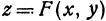 по
по 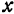 называется приращение функции, вычисленное в предположении, что все независимые переменные, кроме
называется приращение функции, вычисленное в предположении, что все независимые переменные, кроме 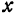 , сохраняют постоянные значения.
, сохраняют постоянные значения.
Например, если дана функция 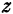
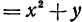 , то ее частное приращение по
, то ее частное приращение по 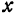 найдем так: дадим
найдем так: дадим 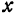 приращение
приращение 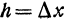 , оставляя без изменения другое переменное
, оставляя без изменения другое переменное 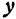 , получим
, получим 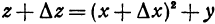 , вычитая первоначальное значение функции, будем иметь
, вычитая первоначальное значение функции, будем иметь
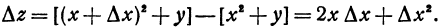
Это и есть частное приращение по 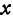 . Аналогично определяются и другие частные приращения.
. Аналогично определяются и другие частные приращения.
Из определения частной производной вытекает, что частная производная по 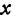 есть предел отношения частного приращения функции по
есть предел отношения частного приращения функции по 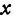 к приращению
к приращению 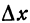 при условии, что приращение
при условии, что приращение 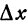 стремится к нулю, т. е.
стремится к нулю, т. е.
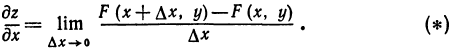
Выясним геометрический смысл частной производной для функции двух независимых переменных (рис. 106).
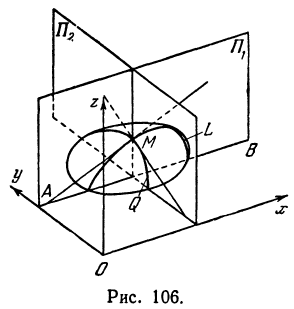
На рисунке 106 изображена поверхность, заданная уравнением 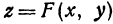 . На поверхности отмечена точка
. На поверхности отмечена точка 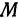 , и через нее проведена плоскость
, и через нее проведена плоскость 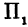 , параллельная координатной плоскости
, параллельная координатной плоскости 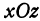 . Все точки, лежащие в плоскости
. Все точки, лежащие в плоскости 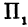 , имеют одну и ту же ординату, т. е. в ней у постоянен.
, имеют одну и ту же ординату, т. е. в ней у постоянен.
В сечении поверхности плоскостью 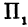 , получается кривая линия, которую обозначим буквой
, получается кривая линия, которую обозначим буквой 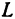 . Формула
. Формула 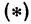 для этой кривой определяет тангенс угла, образованного касательной и прямой
для этой кривой определяет тангенс угла, образованного касательной и прямой 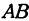 . Иначе можно сказать, что
. Иначе можно сказать, что 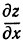 есть тангенс угла между плоскостью
есть тангенс угла между плоскостью 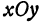 и касательной, проведенной к кривой
и касательной, проведенной к кривой 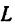 .
.
Также, если проведем через точку 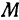 плоскость
плоскость 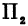 , параллельную плоскости
, параллельную плоскости 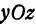 , то получим кривую
, то получим кривую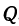 , лежащую в плоскости
, лежащую в плоскости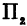 . Частная производная
. Частная производная 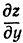 будет давать тангенс угла между плоскостью
будет давать тангенс угла между плоскостью 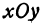 и касательной, проведенной к кривой
и касательной, проведенной к кривой 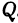 .
.
Покажем применение частных производных. Для этого предварительно дадим некоторые определения.
Значение функции 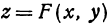 при
при  и
и 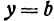 , т. е.
, т. е. 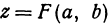 , называется максимальным, если оно больше всех значений функции при
, называется максимальным, если оно больше всех значений функции при 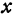 и
и 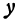 , мало отличающихся соответственно от
, мало отличающихся соответственно от 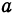 и
и 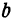 .
.
Иначе говоря, можно найти кусок плоскости 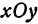 , содержащий точку
, содержащий точку 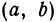 внутри себя и такой, что в любой его внутренней точке, кроме
внутри себя и такой, что в любой его внутренней точке, кроме 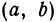 , функция будет иметь значение, меньше чем
, функция будет иметь значение, меньше чем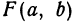 .
.
Минимальное значение функции определяется сходным образом: Значение функции называется минимальным при 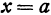 ,
, 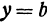 , если оно меньше всех ее значений при
, если оно меньше всех ее значений при 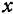 и
и 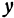 , мало отличающихся соответственно от
, мало отличающихся соответственно от 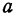 и
и 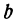 .
.
Например, функция 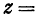
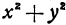 имеет минимум, равный 0, так как при
имеет минимум, равный 0, так как при 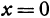 и
и 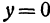 функция равна 0, а при любых других значениях
функция равна 0, а при любых других значениях 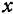 и
и 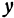 она положительна, т. е. больше нуля.
она положительна, т. е. больше нуля.
Геометрически ясно, что максимальное значение функции определяет точку, находящуюся выше соседних, минимальное же значение определяет точку, находящуюся ниже соседних.
Если употребить географические термины, то максимальные значения функции определяют горные вершины, а минимальные— низины. Также геометрически ясно, что касательная в вершине, проведенная к любой кривой, лежащей на поверхности и проходящей через вершину, параллельна плоскости 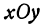 .
.
Значит, частные производные 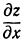 и
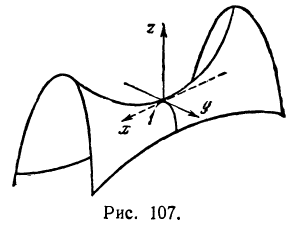
и 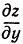 в вершине (и в низине) равны нулю. Однако может случиться, что частные производные равны нулю в некоторой точке, но в ней нет ни максимума, ни минимума. Такие точки называются седловинами. Например, поверхность, изображенная на рис. 107, в начале координат имеет седловину. В самом деле, в сечении с плоскостью
в вершине (и в низине) равны нулю. Однако может случиться, что частные производные равны нулю в некоторой точке, но в ней нет ни максимума, ни минимума. Такие точки называются седловинами. Например, поверхность, изображенная на рис. 107, в начале координат имеет седловину. В самом деле, в сечении с плоскостью 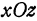 получается кривая, имеющая в начале координат минимум, а в сечении с плоскостью
получается кривая, имеющая в начале координат минимум, а в сечении с плоскостью 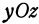 получается кривая, имеющая в начале координат максимум. Обе частные производные
получается кривая, имеющая в начале координат максимум. Обе частные производные 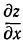 и
и 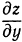 равны нулю, но для поверхности нет ни максимума, минимума.
равны нулю, но для поверхности нет ни максимума, минимума.
Когда мы уверены в существовании максимума или минимума, то их можно найти при помощи частных производных.
Пример:
Найти точку параболоида 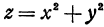 наиболее близкую к точке
наиболее близкую к точке 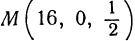 .
.
Решение:
Прежде всего посмотрим, не лежит ли точка 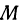 на параболоиде. Если лежит, то она и будет искомой. Если же нет, то расстояние от точки
на параболоиде. Если лежит, то она и будет искомой. Если же нет, то расстояние от точки 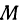 до любой точки параболоида всегда будет больше нуля.
до любой точки параболоида всегда будет больше нуля.
Подставим координаты 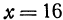 ,
, 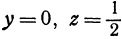 в уравнение параболоида, получим
в уравнение параболоида, получим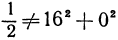 . Значит, точка
. Значит, точка  не лежит на параболоиде. Рассмотрим теперь произвольную точку параболоида, для нее
не лежит на параболоиде. Рассмотрим теперь произвольную точку параболоида, для нее  и
и 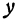 произвольны, a
произвольны, a 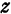 находится из уравнения
находится из уравнения 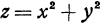 . Следовательно, координаты произвольной точки
. Следовательно, координаты произвольной точки 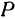 параболоида будут
параболоида будут 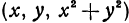 . Напишем формулу, выражающую расстояние между точками
. Напишем формулу, выражающую расстояние между точками 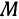 и
и 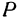 ):
):
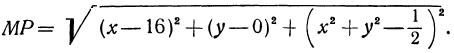
Это расстояние (эта функция), как мы только что убедились, никогда не равно нулю, но оно может быть сколь угодно большим. Если частные производные обращаются в какой-то одной точке в нуль, то в этой точке возможно существование минимума. Если расстояние минимальное, то и его квадрат также будет иметь минимальное значение. Поэтому вместо расстояния 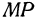 будем рассматривать его квадрат, который обозначим буквой
будем рассматривать его квадрат, который обозначим буквой 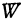 . Таким образом, получилась следующая задача: найти минимум функции
. Таким образом, получилась следующая задача: найти минимум функции
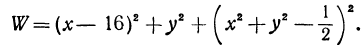
Вычислим частные производные:
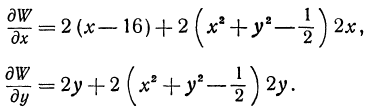
Приравниваем их нулю:
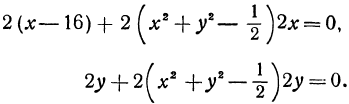
Решим полученную систему уравнений
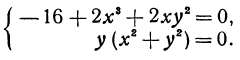
Из второго уравнения или 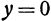 , или
, или 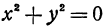 . Если
. Если 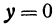 , то из первого уравнения получаем, что
, то из первого уравнения получаем, что 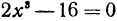 , откуда
, откуда 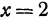 . Если же
. Если же 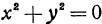 , то
, то 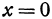 и
и 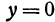 ; подставляя в первое уравнение, получаем —16 = 0, т. е. эти значения ему не удовлетворяют. Таким образом, решением системы являются только
; подставляя в первое уравнение, получаем —16 = 0, т. е. эти значения ему не удовлетворяют. Таким образом, решением системы являются только 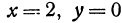 . Следовательно, точка параболоида, ближайшая к точке
. Следовательно, точка параболоида, ближайшая к точке 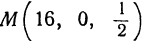 , найдена, это
, найдена, это 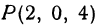 .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |