
Функции, их свойства и графики с примерами решения
Содержание:
Функции, их свойства и графики
В этом параграфе вы повторите основные сведения о функции; узнаете, что называют наибольшим и наименьшим значениями функции на множестве, какие функции называют четными, а какие - нечетными; ознакомитесь со свойствами графиков четных и нечетных функций.
Вы узнаете, какую функцию называют стеленной функцией с целым показателем, какими свойствами обладает эта функция; что называют корнем 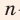
Вы научитесь извлекать корни 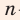 -й степени; выполнять возведение в степень с рациональным показателем; преобразовывать выражения, содержащие степени с рациональными показателями и корни
-й степени; выполнять возведение в степень с рациональным показателем; преобразовывать выражения, содержащие степени с рациональными показателями и корни 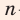 -й степени; решать иррациональные уравнения.
-й степени; решать иррациональные уравнения.
Наибольшее и наименьшее значения функции. Четные и нечетные функции
Перед изучением этого пункта рекомендуем выполнить упражнения 1.24-1.28.
В 7 классе вы ознакомились с понятием функции и при изучении многих разделов курса алгебры неоднократно обращались к этому понятию. Такую важную роль функция играет не случайно: ведь математическими моделями многих реальных процессов служат именно функции. Вам знакомы такие понятия, как область определения, область значений, нули, промежутки знакопостоянства, промежутки возрастания и убывания функции. Например, для функции 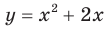 , график которой изображен на рисунке 1.1, имеем:
, график которой изображен на рисунке 1.1, имеем:
- область определения:
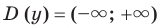 ;
; - область значений:
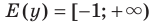 ;
; - нули: числа -2 и О;
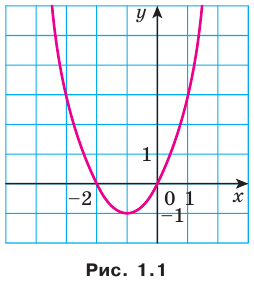
- промежутки знакопостоянства: функция принимает положительные значения на каждом из промежутков
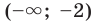 и
и 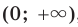 , а отрицательные значения — на промежутке (-2; 0);
, а отрицательные значения — на промежутке (-2; 0); - промежутки возрастания и убывания: функция убывает на промежутке ■ -1] и возрастает на промежутке
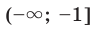 .
.
Приведенный выше перечень далеко не исчерпывает те свойства, которые целесообразно изучать при исследовании функции. Рассмотрим новые понятия, помогающие более полно охарактеризовать функцию.
Определение. Число 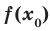 называют наибольшим значением функции
называют наибольшим значением функции 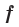 на множестве
на множестве 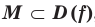 , если существует такое число
, если существует такое число 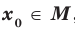 , что для всех
, что для всех 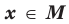 выполняется неравенство
выполняется неравенство 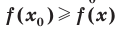 .
.
Обозначают: 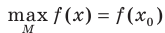 .
.
Определение. Число 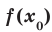 называют наименьшим значением функции
называют наименьшим значением функции 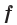 на множестве
на множестве 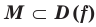 , если существует такое число
, если существует такое число 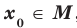 , что для всех
, что для всех 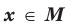 выполняется неравенство
выполняется неравенство 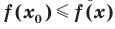 . Обозначают:
. Обозначают: 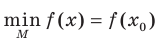 .
.
Рассмотрим несколько примеров.
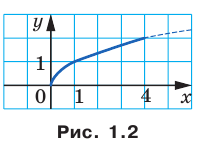
Для функции 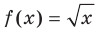 и множества
и множества 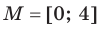 имеем (рис. 1.2):
имеем (рис. 1.2): 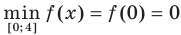 ,
, 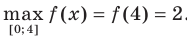 .
.
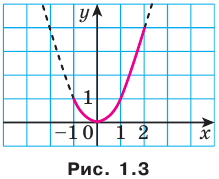
Для функции 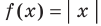 и множества
и множества 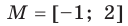 имеем (рис. 1.3):
имеем (рис. 1.3): 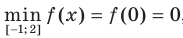 ,
, 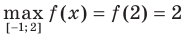 .
.
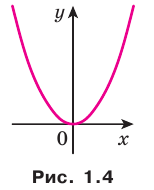
He каждая функция на заданном множестве имеет наименьшее или наибольшее значение. Так, для функции 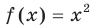 имеем:
имеем: 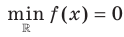 . Наибольшего значения на множестве действительных чисел эта функция не имеет (рис. 1.4).
. Наибольшего значения на множестве действительных чисел эта функция не имеет (рис. 1.4).
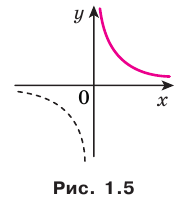
Функция 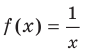 на множестве
на множестве 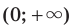 не имеет ни наибольшего, ни наименьшего значений (рис. 1.5).
не имеет ни наибольшего, ни наименьшего значений (рис. 1.5).
Определение. Функцию 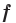 называют четной, если для любого
называют четной, если для любого 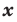 из области определения выполняется равенство
из области определения выполняется равенство 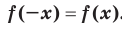 .
.
Определение. Функцию 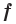 называют нечетной, если для любого
называют нечетной, если для любого 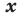 из области определения выполняется равенство
из области определения выполняется равенство 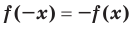 .
.
Например, функция 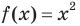 — четная, а функция
— четная, а функция 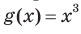 — нечетная. Действительно,
— нечетная. Действительно, 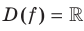 ,
, 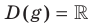 . Для любого
. Для любого 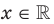 выполняются равенства
выполняются равенства 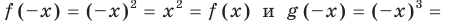
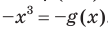 .
.
Выполнение равенства 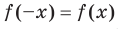 или равенства
или равенства 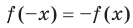 для любого
для любого 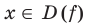 означает, что область определения функции
означает, что область определения функции 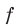 симметрична относительно начала координат, то есть обладает следующим свойством: если
симметрична относительно начала координат, то есть обладает следующим свойством: если 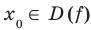 , то
, то 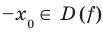 .
.
Из приведенных определений следует, что если область определения функции не симметрична относительно начала координат, то эта функция не может быть ни четной, ни нечетной.
Например, областью определения функции 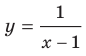 является множество
является множество 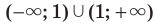 , которое не симметрично относительно начала координат. Поэтому данная функция не является ни четной, ни нечетной.
, которое не симметрично относительно начала координат. Поэтому данная функция не является ни четной, ни нечетной.
Пример:
Докажите, что функция 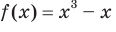 является нечетной.
является нечетной.
Решение:
Поскольку 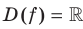 , то область определения функции
, то область определения функции 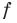 симметрична относительно начала координат. Для любого
симметрична относительно начала координат. Для любого 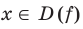 имеем:
имеем: 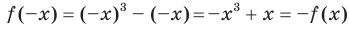
Следовательно, функция f нечетная. ◄
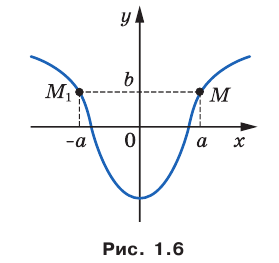
Теорема 1.1. Ось ординат является осью симметрии графика четной функции.
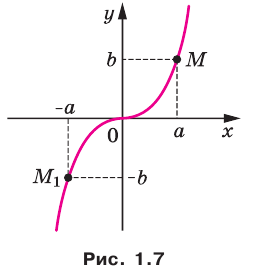
Теорема 1.2. Начало координат является центром симметрии графика нечетной функции.
Утверждения теорем 1.1 и 1.2 проиллюстрированы на рисунках 1.6 и 1.7.
Степенная функция с натуральным показателем
Свойства и графики функций 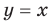 и
и 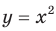 хорошо знакомы вам из курсов математики предыдущих классов. Эти функции являются частными случаями функции
хорошо знакомы вам из курсов математики предыдущих классов. Эти функции являются частными случаями функции 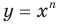 ,
, 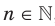 , которую называют степенной функцией с натуральным показателем.
, которую называют степенной функцией с натуральным показателем.
Поскольку выражение 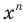 ,
, 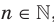 , имеет смысл при любом
, имеет смысл при любом 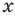 , то областью определения степенной, функции с натуральным показателем является множество
, то областью определения степенной, функции с натуральным показателем является множество 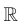 .
.
Очевидно, что рассматриваемая функция имеет единственный нуль 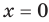 .
.
Дальнейшее исследование свойств функции 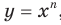 ,
, 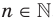 , проведем для двух случаев:
, проведем для двух случаев: 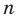 — четное натуральное число и
— четное натуральное число и 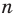 — не четное натуральное число.
— не четное натуральное число.
Первый случай:  .
.
Отметим, что при 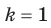 получаем функцию
получаем функцию 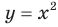 , свойства и гра фик которой были рассмотрены в курсе алгебры 8 класса.
, свойства и гра фик которой были рассмотрены в курсе алгебры 8 класса.
Поскольку при любом 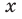 выражение
выражение 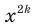 принимает только не отрицательные значения, то область значений рассматриваемой функции не содержит ни одного отрицательного числа.
принимает только не отрицательные значения, то область значений рассматриваемой функции не содержит ни одного отрицательного числа.
Можно показать, что для любого 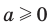 существует такое значение аргумента
существует такое значение аргумента 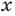 , что
, что 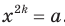 .
.
 Сказанное означает, что областью значений функции
Сказанное означает, что областью значений функции 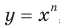 , где
, где 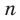 — четное натуральное число, является множество
— четное натуральное число, является множество 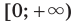 . Если
. Если 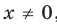 , то
, то 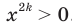 .
. Следовательно, промежутки
Следовательно, промежутки 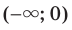 и
и 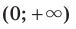 являются промежутками знакопостоянства функции
являются промежутками знакопостоянства функции 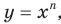 где
где 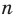 — четное натуральное число.
— четное натуральное число. Функция
Функция 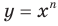 , где
, где 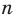 — четное натуральное число, является четной. Действительно, для любого
— четное натуральное число, является четной. Действительно, для любого 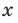 из области определения выполняется равенство
из области определения выполняется равенство 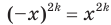 .
.
Рассмотрим произвольные числа 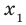 и
и 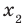 такие, что
такие, что 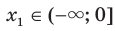 ,
, 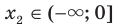 и
и 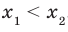 . Тогда
. Тогда 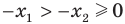 . Воспользовавшись свойством числовых неравенств, получаем:
. Воспользовавшись свойством числовых неравенств, получаем: 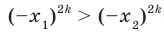 . Отсюда
. Отсюда 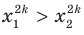
 Следовательно, функция
Следовательно, функция 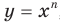 , где
, где 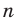 — четное натуральное число, убывает на промежутке
— четное натуральное число, убывает на промежутке 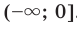 . Аналогично можно показать, что эта функция возрастает на промежутке
. Аналогично можно показать, что эта функция возрастает на промежутке 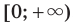 .
.
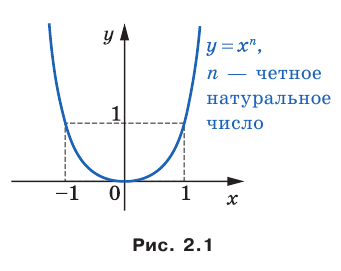
Полученные свойства позволяют схематически изобразить график функции 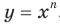 , где
, где 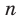 — четное натуральное число (рис. 2.1). В частности, график функции
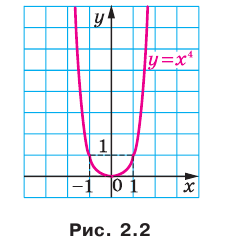
— четное натуральное число (рис. 2.1). В частности, график функции 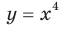 изображен на рисунке 2.2.
изображен на рисунке 2.2.
Второй случай: 
Отметим, что при 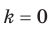 получаем функцию
получаем функцию 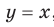 , свойства и график которой были рассмотрены в курсе алгебры 7 класса.
, свойства и график которой были рассмотрены в курсе алгебры 7 класса.
Теперь пусть 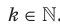 .
.
Можно показать, что для любого 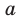 существует такое значение аргумента
существует такое значение аргумента 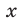 , что
, что 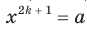 .
.
 Сказанное означает, что областью значений функции
Сказанное означает, что областью значений функции 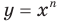 , где
, где 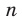 — нечетное натуральное число, является множество
— нечетное натуральное число, является множество 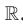 .
.
Если 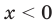 , то
, то 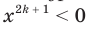 ; если
; если 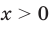 , то
, то 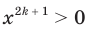 .
.
 Следовательно, промежутки
Следовательно, промежутки 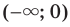 и
и 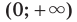 являются промежутками знакопостоянства функции
являются промежутками знакопостоянства функции 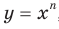 , где
, где 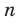 — нечетное натуральное число.
— нечетное натуральное число. Функция
Функция 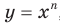 , где
, где 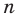 — нечетное натуральное число, является нечетной. Действительно, для любого
— нечетное натуральное число, является нечетной. Действительно, для любого 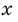 из области определения выполняется равенство
из области определения выполняется равенство 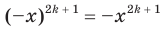 .
.
Рассмотрим произвольные числа 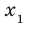 и
и 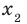 такие, что
такие, что 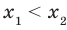 . Воспользовавшись свойством числовых неравенств, получаем:
. Воспользовавшись свойством числовых неравенств, получаем:
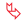 Следовательно, функция
Следовательно, функция 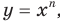 где
где 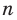 — нечетное натуральное число, является возрастающей.
— нечетное натуральное число, является возрастающей.
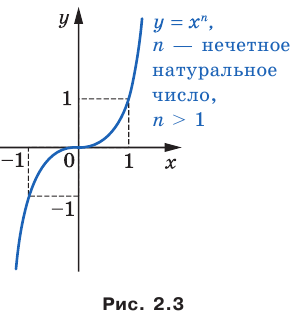
Полученные свойства позволяют схематически изобразить график функции 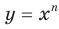 , где
, где 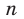 — нечетное натуральное число,
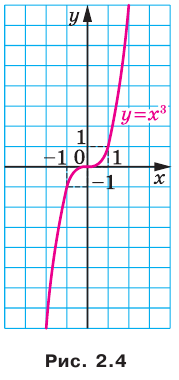
— нечетное натуральное число,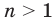 (рис. 2.3). В частности, график функции
(рис. 2.3). В частности, график функции 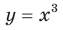 изображен на рисунке 2.4.
изображен на рисунке 2.4.
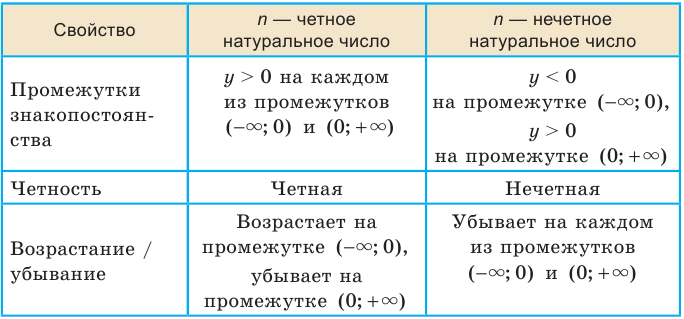
В таблице приведены свойства функции  ,
,  , установленные в этом пункте.
, установленные в этом пункте.
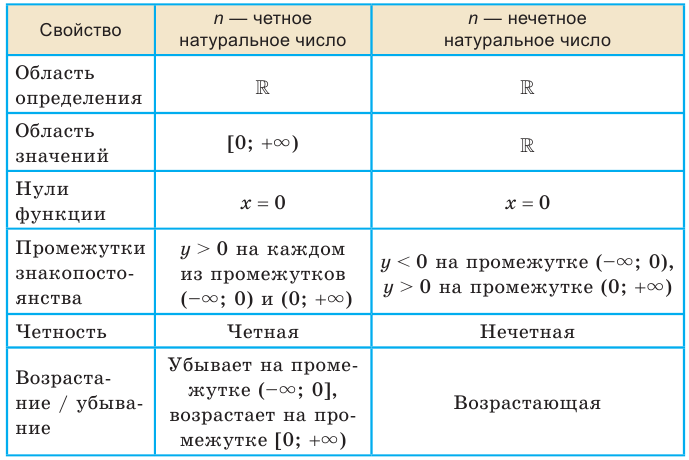
Степенная функция с целым показателем
Функцию, которую можно задать формулой 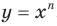 , где
, где 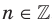 , называют степенной функцией с целым показателем. Свойства этой функции для натурального показателя были рассмотрены в предыдущем пункте. Здесь мы рассмотрим случаи, когда показатель п является целым отрицательным числом или нулем.
, называют степенной функцией с целым показателем. Свойства этой функции для натурального показателя были рассмотрены в предыдущем пункте. Здесь мы рассмотрим случаи, когда показатель п является целым отрицательным числом или нулем.
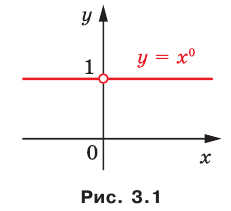
Областью определения функции 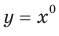 является множество
является множество 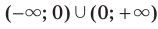 . областью значений — одноэлементное множество {1}. График этой функции изображен на рисунке 3.1.
. областью значений — одноэлементное множество {1}. График этой функции изображен на рисунке 3.1.
Рассмотрим функцию 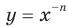 , где
, где  .
.
С частным случаем этой функции, когда 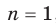 , то есть с функцией
, то есть с функцией 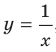 , вы знакомы из курса алгебры 8 класса. Запишем функцию
, вы знакомы из курса алгебры 8 класса. Запишем функцию 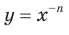 в виде
в виде 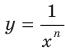 .
.
Тогда становится понятно, что областью определения функции 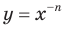 ,
, 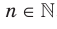 , является множество
, является множество 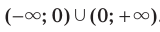 .
.
Очевидно, что эта функция нулей не имеет.
Дальнейшее исследование свойств функции 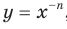 , где
, где 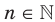 , проведем для двух случаев:
, проведем для двух случаев: 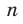 — четное натуральное число и
— четное натуральное число и 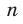 — нечетное натуральное число.
— нечетное натуральное число.
Первый случай: 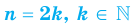 .
.
Имеем: 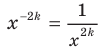 Так как выражение
Так как выражение 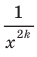 принимает только положительные значения, то в область значений рассматриваемой функции не входят отрицательные числа, а также число 0. Можно показать, что для любого
принимает только положительные значения, то в область значений рассматриваемой функции не входят отрицательные числа, а также число 0. Можно показать, что для любого  существует такое значение аргумента
существует такое значение аргумента  , что
, что 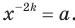
 Сказанное означает, что областью значений функции
Сказанное означает, что областью значений функции 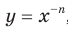 , где
, где 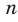 — четное натуральное число, является множество
— четное натуральное число, является множество 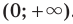 .
. Поскольку для любого
Поскольку для любого 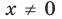 выполняется неравенство
выполняется неравенство 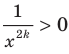 то промежутки
то промежутки 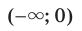 и
и 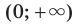 являются промежутками знакопостоянства функции
являются промежутками знакопостоянства функции 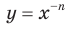 , где
, где 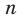 — четное натуральное число.
— четное натуральное число. Функция
Функция 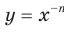 , где
, где 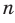 — четное натуральное число, является четной.
— четное натуральное число, является четной.
Действительно, для любого 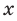 из области определения выполняется равенство
из области определения выполняется равенство 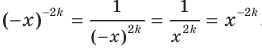
Рассмотрим произвольные числа 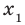 и
и 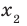 такие, что
такие, что 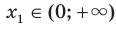 ,
, 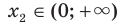 и
и 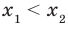 . Воспользовавшись свойством числовых неравенств, получаем:
. Воспользовавшись свойством числовых неравенств, получаем: 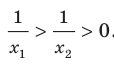 Отсюда
Отсюда 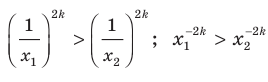
 Следовательно, функция
Следовательно, функция 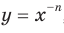 , где
, где 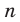 — четное натуральное число, убывает на промежутке
— четное натуральное число, убывает на промежутке 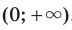 .
. Можно также показать, что функция
Можно также показать, что функция 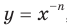 , где
, где 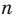 — четное натуральное число, возрастает на промежутке
— четное натуральное число, возрастает на промежутке 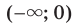 .
.
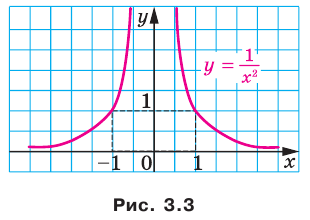
Заметим, что с увеличением модуля 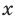 значения выражения
значения выражения 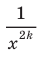 X,
X,  , становятся все меньшими и меньшими. Поэтому расстояние от точки графика функции
, становятся все меньшими и меньшими. Поэтому расстояние от точки графика функции 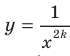 , до оси абсцисс уменьшается с увеличением модуля абсциссы точки и может стать сколь угодно малым, но никогда не будет равным нулю.
, до оси абсцисс уменьшается с увеличением модуля абсциссы точки и может стать сколь угодно малым, но никогда не будет равным нулю.
Также можно установить, что с увеличением модуля ординаты расстояние от точки графика функции 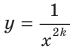 ,
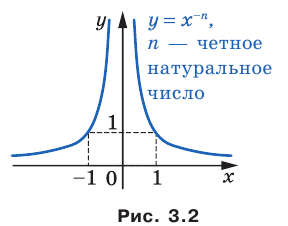
,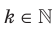 до оси ординат уменьшается и может стать сколь угодно малым, но никогда не будет равным нулю. Полученные свойства позволяют схематически изобразить график функции
до оси ординат уменьшается и может стать сколь угодно малым, но никогда не будет равным нулю. Полученные свойства позволяют схематически изобразить график функции 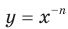 , где
, где 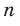 — четное натуральное число (рис. 3.2). В частности, график функции
— четное натуральное число (рис. 3.2). В частности, график функции 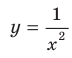 изображен на рисунке 3.3.
изображен на рисунке 3.3.
Второй случай: 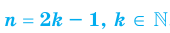 .
.
Можно показать, что для любого 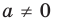 существует такое значение аргумента
существует такое значение аргумента 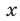 , что
, что 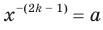 .
.
 Сказанное означает, что областью значений функции
Сказанное означает, что областью значений функции 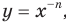 где
где 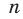 — нечетное натуральное число, является множество
— нечетное натуральное число, является множество 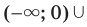
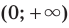 . Если
. Если 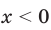 , то
, то 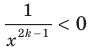 ; если
; если 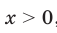 , то
, то 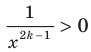 .
. Следовательно, промежутки
Следовательно, промежутки 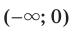 и
и 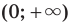 являются промежутками знакопостоянства функции
являются промежутками знакопостоянства функции 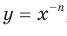 , где
, где 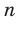 — нечетное натуральное число.
— нечетное натуральное число. Функция
Функция 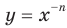 , где
, где 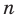 — нечетное натуральное число, является нечетной. Действительно, для любого
— нечетное натуральное число, является нечетной. Действительно, для любого 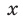 из области определения выполняется равенство
из области определения выполняется равенство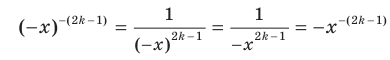
 Можно показать, что функция
Можно показать, что функция 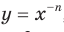 , где
, где 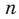 — нечетное натуральное число, убывает на каждом из промежутков
— нечетное натуральное число, убывает на каждом из промежутков 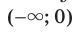 и
и 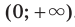 .
.
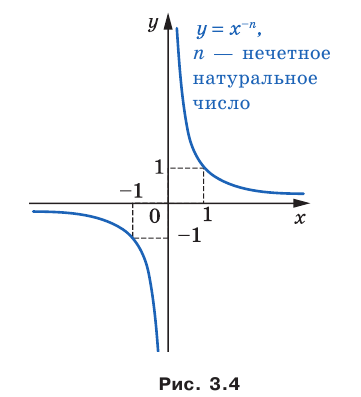
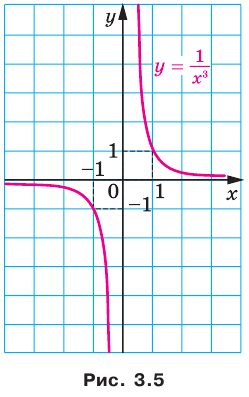
Полученные свойства позволяют схематически изобразить график функции 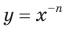 , где
, где 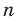 — нечетное натуральное число (рис. 3.4). В частности, график функции
— нечетное натуральное число (рис. 3.4). В частности, график функции 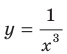 изображен на рисунке 3.5.
изображен на рисунке 3.5.
В таблице приведены свойства функции 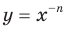 ,
, 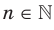 , изученные в этом пункте.
, изученные в этом пункте.

Определение корня n-й степени
Вы знаете, что корнем второй степени (квадратным корнем) из числа а называют такое число, вторая степень которого равна  . Аналогично дают определение корня
. Аналогично дают определение корня  степени из числа
степени из числа  , где
, где 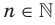 ,
, 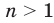 .
.
Определение. Корнем 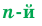 степени из числа
степени из числа 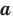 , где
, где 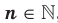 .
. 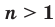 , называют такое число,
, называют такое число, 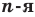 степень которого равна
степень которого равна 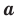 .
.
Например, корнем пятой степени из числа 32 является число 2, так как 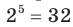 ; корнем третьей степени из числа -64 является число -4, так как
; корнем третьей степени из числа -64 является число -4, так как 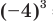 = -64; корнями четвертой степени из числа 81 являются числа 3 и -3, так как
= -64; корнями четвертой степени из числа 81 являются числа 3 и -3, так как 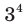 = 81 и
= 81 и 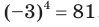 .
.
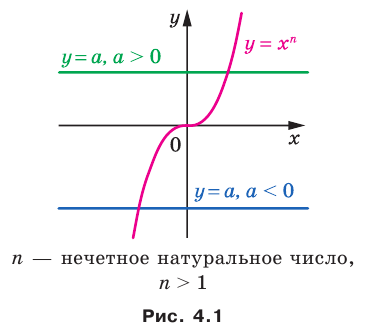
Если 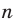 — нечетное натуральное число, то графики функций
— нечетное натуральное число, то графики функций 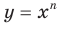 и
и 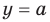 при любом
при любом 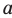 пересекаются в одной точке (рис. 4.1).
пересекаются в одной точке (рис. 4.1).
Это означает, что уравнение 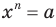 имеет единственный корень при любом
имеет единственный корень при любом  .
.
Тогда можно сделать следующий вывод: если  — нечетное натуральное число, большее 1, то из любого числа существует корень
— нечетное натуральное число, большее 1, то из любого числа существует корень 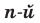 степени, причем только один.
степени, причем только один.
Корень нечетной степени 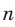 ,
, 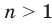 , из числа
, из числа 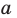 обозначают так:
обозначают так: 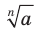 (читают: «корень
(читают: «корень 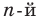 степени из а»). Например,
степени из а»). Например, 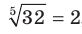 ,
,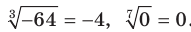 .
.
Знак 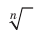 называют знаком корня
называют знаком корня 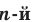 степени или радикалом.
степени или радикалом.
Выражение, стоящее под радикалом, называют подкоренным выражением.
Корень третьей степени принято называть также кубическим корнем.
Например, запись 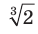 читают: «кубический корень из числа 2».
читают: «кубический корень из числа 2».
Подчеркнем, что выражение 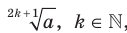 определено при любом
определено при любом 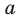 .
.
Из определения корня 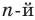 степени следует, что при любом
степени следует, что при любом 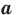 выполняется равенство
выполняется равенство
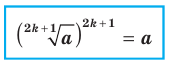
Например,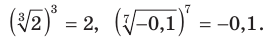
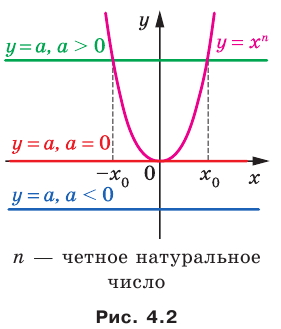
Рассмотрим уравнение 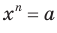 , где
, где 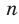 — четное натуральное число.
— четное натуральное число.
Из рисунка 4.2 видно: если 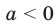 , то графики функций
, то графики функций 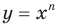 и
и 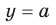 не имеют общих точек; если
не имеют общих точек; если 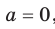 то рассматриваемые графики имеют одну общую точку; если
то рассматриваемые графики имеют одну общую точку; если 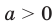 , то общих точек две, причем их абсциссы — противоположные числа.
, то общих точек две, причем их абсциссы — противоположные числа.
Тогда можно сделать следующий вывод: если 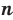 — четное натуральное число, то при
— четное натуральное число, то при 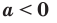 корень
корень 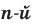 степени из числа
степени из числа 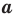 не существует; при
не существует; при 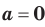 корень
корень 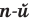 степени из числа
степени из числа 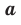 равен О; при
равен О; при 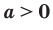 существуют два противоположных числа, каждое из которых является корнем
существуют два противоположных числа, каждое из которых является корнем 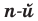 степени из числа
степени из числа  .
.
Вы знаете, что арифметическим квадратным корнем из неотрицательного числа 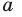 называют такое неотрицательное число, вторая степень которого равна
называют такое неотрицательное число, вторая степень которого равна 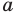 . Аналогично дают определение арифметического корня
. Аналогично дают определение арифметического корня 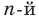 степени.
степени.
Определение. Арифметическим корнем 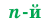 степени из неотрицательного числа
степени из неотрицательного числа 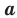 , где
, где 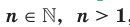 , называют такое неотрицательное число,
, называют такое неотрицательное число, 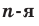 степень которого равна
степень которого равна 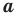 .
.
Арифметический корень 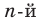 степени из неотрицательного числа
степени из неотрицательного числа 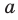 обозначают так:
обозначают так: 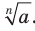 .
.
Например, 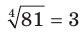 , поскольку
, поскольку 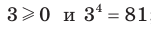 ;
;
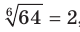 , поскольку
, поскольку 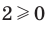 и
и 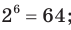
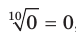 , поскольку
, поскольку 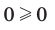 и
и 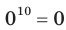 .
.
Вообще, если 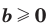 и
и 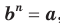 , где
, где 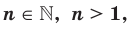 то
то 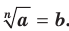 С помощью знака корня
С помощью знака корня 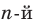 степени можно записывать корни уравнения
степени можно записывать корни уравнения 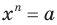 , где
, где 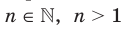 .
.
Например, корнем уравнения 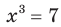 является единственное число
является единственное число 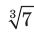 ; корнями уравнения
; корнями уравнения 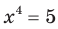 являются два числа:
являются два числа: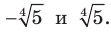
Из определения арифметического корня 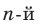 степени следует, что:
степени следует, что:
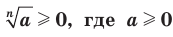 (например, -
(например, -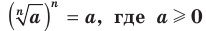 , где а > 0 (например,
, где а > 0 (например, 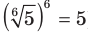 );
);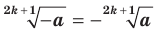 (например,
(например, 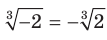 ).
).
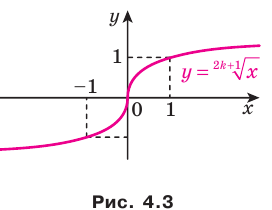
Выше было установлено, что корень нечетной степени из любого числа существует и принимает единственное значение. Поэтому каждому действительному числу х можно поставить в соответствие единственное число у такое, что 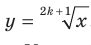 . Указанное правило задает функцию
. Указанное правило задает функцию 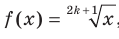 , где
, где 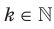 , с областью определения R.
, с областью определения R.
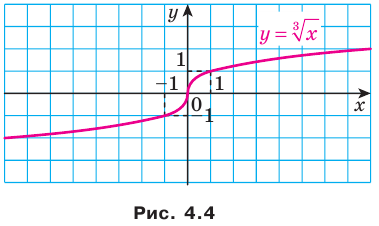
График этой функции изображен на рисунке 4.3. На рисунке 4.4 изображен график функции 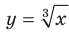 .
.
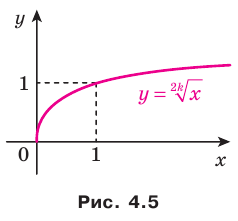
Аналогично определяют функцию 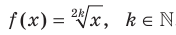 . Областью Определения этой функции является промежуток
. Областью Определения этой функции является промежуток 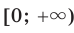 .
.
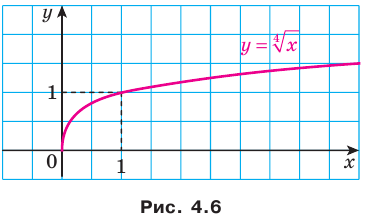
На рисунке 4.5 изображен график функции 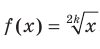 , а на рисунке 4.6 — график функции
, а на рисунке 4.6 — график функции 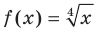 .
.
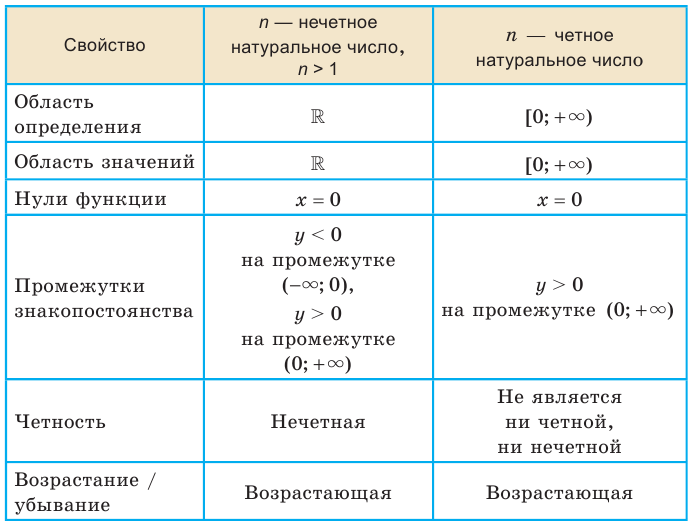
В таблице приведены свойства функции 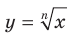 .
.
Пример:
Решите неравенство: 1) 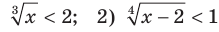 .
.
Решение:
1) Данное неравенство перепишем следующим образом: 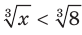 . Поскольку функция
. Поскольку функция 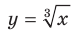 является возрастающей, то можно сделать вывод, что
является возрастающей, то можно сделать вывод, что 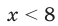 . Ответ:
. Ответ: 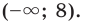
2) Имеем: 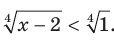 Поскольку функция
Поскольку функция 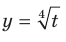 является возрастающей и определена на множестве
является возрастающей и определена на множестве 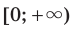 , то данное неравенство равносильно системе
, то данное неравенство равносильно системе 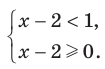 Отсюда
Отсюда 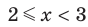 .
.
Ответ: [2; 3). ◄
Свойства корня n-й степени
Свойства корня 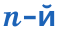 степени
степени
Рассмотрим теоремы, выражающие свойства корня 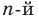 степени. Теорема 5.1 (первая теорема о корне из степени). Для любого
степени. Теорема 5.1 (первая теорема о корне из степени). Для любого 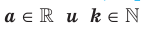 выполняются равенства:
выполняются равенства:
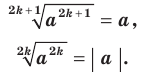
Доказательство. Чтобы доказать равенство 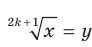 , достаточно показать, что
, достаточно показать, что 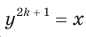 . Для первого доказываемого равенства
. Для первого доказываемого равенства 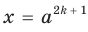 и
и 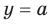 . Отсюда равенство
. Отсюда равенство 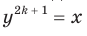 очевидно.
очевидно.
Чтобы доказать равенство 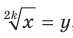 , достаточно показать, что
, достаточно показать, что 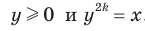 . Для второго доказываемого равенства имеем:
. Для второго доказываемого равенства имеем: 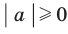 и
и 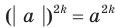 .
.
Теорема 5.2 (корень из произведения). Если 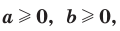
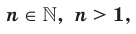 , то
, то
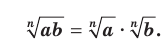
Доказательство. Для того чтобы доказать равенство 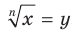 , где
, где 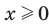 , достаточно показать, что
, достаточно показать, что 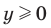 и
и 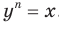 . Имеем:
. Имеем: 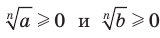 . Тогда
. Тогда 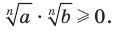
Кроме того, 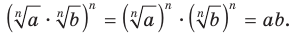
Теорем а 5.3 (корень из частного). Если 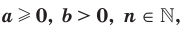
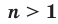 , то
, то 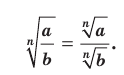
Теорема 5.4 (степень корня). Если 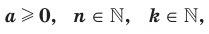
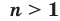 , то
, то
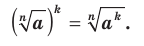
Д о к а за т е л ь с т в о . Если 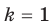 , то доказываемое равенство очевидно. Пусть
, то доказываемое равенство очевидно. Пусть 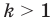 . Имеем:
. Имеем:
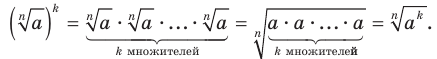
Теорем а 5.5 (корень из корня). Если 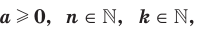
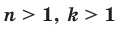 , то
, то 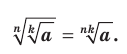
Д о к а за т ел ьст во . Имеем: 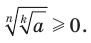 Кроме того,
Кроме того, 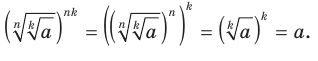
Теорема 5.6 (вторая теорем а о корне из степени). Если 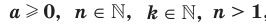 , то
, то
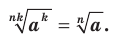
Д о к а за т е л ь с т в о . Если 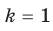 , то доказываемое равенство очевидно.
, то доказываемое равенство очевидно.
Пусть 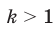 . Имеем:
. Имеем: 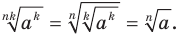
Пример:
Найдите значение выражения:
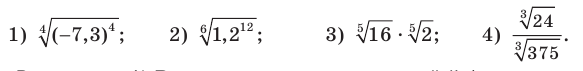
Решение:
1) Воспользовавшись теоремой 5.1, можно записать: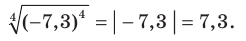 2)
2) 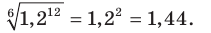 3) Заменив произведение корней корнем из произведения, получим:
3) Заменив произведение корней корнем из произведения, получим: 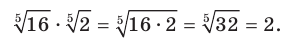
4) Заменив частное корней корнем из частного, получим: 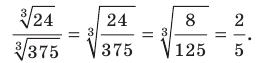
Пример:
Упростите выражение:
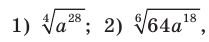 если
если 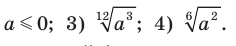
Решение:
1) Применив теорему 5.1, получим:
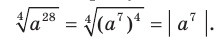 2) Имеем:
2) Имеем: 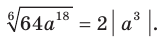 Поскольку по условию
Поскольку по условию 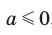 , то
, то 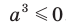 . Тогда
. Тогда 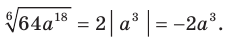
3) 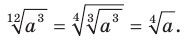 4)
4)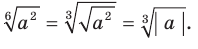
Пример:
Вынесите множитель из-под знака корня: 1) 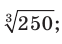 2)
2)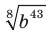 .
.
Решение:
1) Представим число, стоящее под знаком корня, в виде произведения двух чисел, одно из которых является кубом рационального числа, и вынесем множитель из-под знака корня:
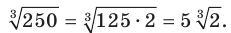
2) Из условия следует, что 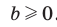 Тогда
Тогда
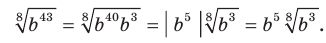
Пример:
Внесите множитель под знак корня:
1) 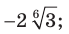 2)
2) 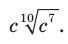
Решение:
1) 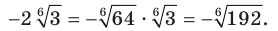
2) Из условия следует, что 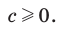 Тогда
Тогда 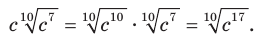
Пример:
Сократите дробь 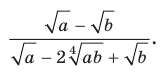
Решение:
Разложив числитель и знаменатель данной дроби на множители, получаем:
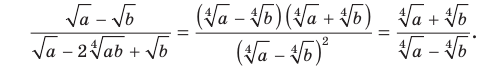
Определение и свойства степени с рациональным показателем
В 7 классе вы узнали, что степень с натуральным показателем обладает следующими свойствами:
1) 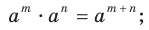 2)
2) 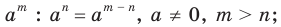
3) 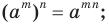
4) 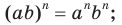 Позже вы ознакомились с определениями степени с нулевым показателем и степени с отрицательным целым показателем:
Позже вы ознакомились с определениями степени с нулевым показателем и степени с отрицательным целым показателем:
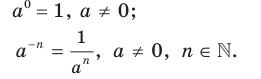 Эти определения весьма удачны: при таком подходе все пять свойств степени с натуральным показателем остаются справедливыми и для степени с целым показателем.
Эти определения весьма удачны: при таком подходе все пять свойств степени с натуральным показателем остаются справедливыми и для степени с целым показателем.
Введем понятие степени с дробным показателем, то есть степени 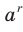 , показатель которой является рациональным числом вида
, показатель которой является рациональным числом вида 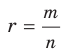 , где
, где 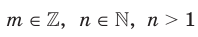 . Желательно сделать это так, чтобы степень с дробным показателем обладала всеми свойствами степени с целым показателем. Подсказкой для такого определения может служить следующий пример. Обозначим через
. Желательно сделать это так, чтобы степень с дробным показателем обладала всеми свойствами степени с целым показателем. Подсказкой для такого определения может служить следующий пример. Обозначим через 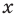 искомое значение степени
искомое значение степени 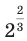 , то есть
, то есть 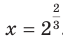
Учитывая свойство 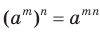 , можем записать:
, можем записать: 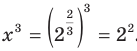 . Следовательно,
. Следовательно, 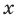 — это кубический корень из числа
— это кубический корень из числа 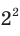 , то есть
, то есть 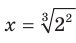 . Таким образом,
. Таким образом, 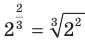 .
.
Эти соображения подсказывают, что целесообразно принять следующее определение.
Определение. Степенью положительного числа 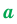 с рациональным показателем
с рациональным показателем  , представленным в виде
, представленным в виде 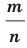 , где
, где 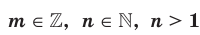 , называют число
, называют число 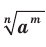 , то есть
, то есть
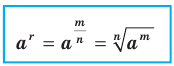
Например,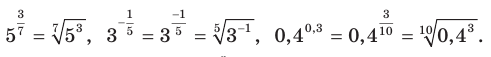
Заметим, что значение степени 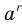 , где
, где 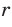 — рациональное число, не зависит от того, в виде какой дроби представлено число
— рациональное число, не зависит от того, в виде какой дроби представлено число 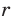 . Это можно показать, используя равенства
. Это можно показать, используя равенства 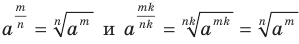 .
.
Степень с основанием, равным нулю, определяют только для положительного рационального показателя.
Определение. 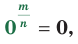 где
где 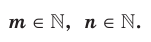 Обратим внимание, что, например, запись
Обратим внимание, что, например, запись 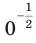 не имеет смысла.
не имеет смысла.
Подчеркнем, что в данных определениях не идет речь о степени 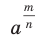 для
для 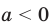 , например, выражение
, например, выражение 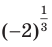 остается неопределенным. Вместе с тем выражение
остается неопределенным. Вместе с тем выражение 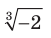 имеет смысл. Возникает естественный вопрос: почему бы не считать, что
имеет смысл. Возникает естественный вопрос: почему бы не считать, что 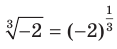 ? Покажем, что такая договоренность привела бы к противоречию:
? Покажем, что такая договоренность привела бы к противоречию: 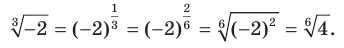
Получили, что отрицательное число 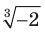 «равно» положительному числу
«равно» положительному числу 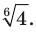 Функцию, которую можно задать формулой
Функцию, которую можно задать формулой 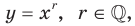 называют степенной функцией с рациональным показателем.
называют степенной функцией с рациональным показателем.
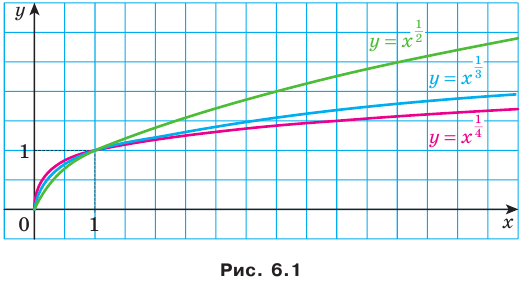
Если несократимая дробь 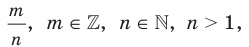 является числом положительным, то областью определения функции
является числом положительным, то областью определения функции 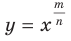 является промежуток
является промежуток 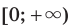 ; а если эта дробь — отрицательное число, то промежуток
; а если эта дробь — отрицательное число, то промежуток 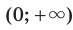 .
.
На рисунке 6.1 изображены графики функций 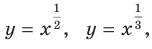
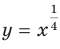 .
.
Покажем, что свойства степени с целым показателем остаются справедливыми и для степени с произвольным рациональным показателем.
Теорема 6.1 (произведение степеней). Для любого 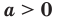 и любых рациональных чисел р и q выполняется равенство
и любых рациональных чисел р и q выполняется равенство
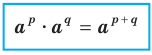
Доказательство. Запишем рациональные числа р и q в виде дробей с одинаковыми знаменателями: 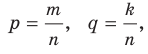 где
где 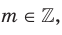
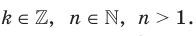 . Имеем:
. Имеем: 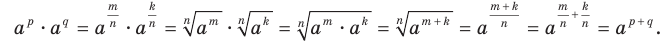
Следствие. Для любого 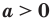 и любого рационального числа
и любого рационального числа 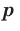 выполняется равенство
выполняется равенство
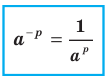
Доказательство. Применяя теорему 6.1, запишем: 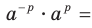
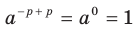 . Отсюда
. Отсюда 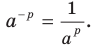
Теорема 6.2 (частное степеней). Для любого 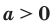 и любых рациональных чисел р и q выполняется равенство
и любых рациональных чисел р и q выполняется равенство
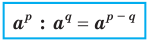
Доказательство. Применяя теорему 6.1, запишем: 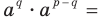
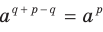 . Отсюда
. Отсюда 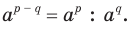
Теорема 6.3 (степень степени). Для любого 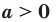 и любых рациональных чисел р и q выполняется равенство
и любых рациональных чисел р и q выполняется равенство
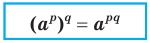
Доказательство. Пусть 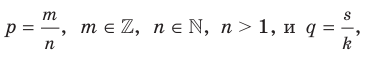
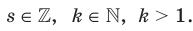 Имеем:
Имеем:
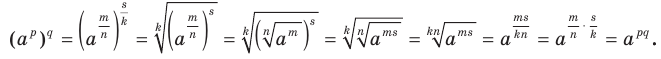
Теорема 6.4 (степень произведения и степень частного). Для любых 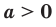 и
и 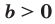 и любого рационального числа
и любого рационального числа 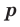 выполняются равенства.
выполняются равенства.
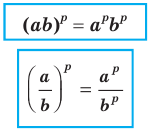
Докажите эту теорему самостоятельно.
Пример:
Упростите выражение
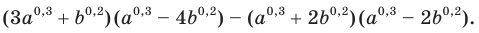
Решение:
Раскроем скобки, используя правило умножения многочленов и формулу разности квадратов, а затем приведем подобные слагаемые:
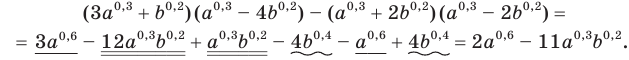
Пример:
Упростите выражение 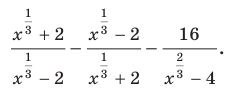
Решение:
Выполним замену 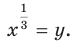 Тогда данное выражение принимает вид
Тогда данное выражение принимает вид 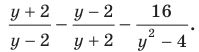 Это выражение легко упростить. Завершите решение самостоятельно. Ответ:
Это выражение легко упростить. Завершите решение самостоятельно. Ответ: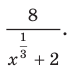
Иррациональные уравнения
При решении уравнений иногда возникает необходимость возвести обе части уравнения в одну и ту же степень. Выясним, как это преобразование влияет на множество корней данного уравнения.
Теорема 7.1. Если обе части уравнения возвести в нечетную степень, то получим уравнение, равносильное данному.
Пример:
Решите уравнение 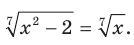
Решение:
Возведем обе части данного уравнения в седьмую степень. Получим равносильное уравнение
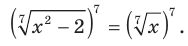
Отсюда 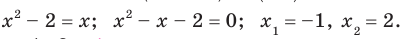 Ответ: -1; 2.
Ответ: -1; 2.
Уравнение, рассмотренное в задаче 1, содержит переменную под знаком корня. Такие уравнения называют иррациональными. Вот еще примеры иррациональных уравнений:
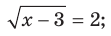
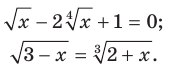 При решении задачи 1 нам пришлось преобразовывать уравнение, содержащее корни нечетной степени. Рассмотрим уравнения, содержащие корни четной степени.
При решении задачи 1 нам пришлось преобразовывать уравнение, содержащее корни нечетной степени. Рассмотрим уравнения, содержащие корни четной степени.
Пример:
Решите уравнение 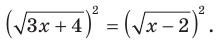 (1)
(1)
Решение:
Применяя формулу 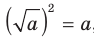 , заменим данное уравнение таким:
, заменим данное уравнение таким: 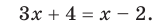 (2) Отсюда
(2) Отсюда 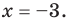
Однако проверка показывает, что число -3 не является корнем исходного уравнения. Говорят, что число -3 является посторонним корнем уравнения (1). Следовательно, уравнение (1) не имеет корней. Ответ: корней нет.
Причина появления постороннего корня при решении задачи 2 заключается в том, что, применив формулу 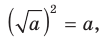 мы не учли ограничение
мы не учли ограничение 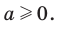 Поэтому уравнение (2) оказалось не равносильным уравнению (1).
Поэтому уравнение (2) оказалось не равносильным уравнению (1).
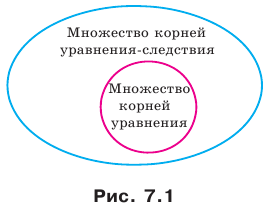
Определение. Если множество корней уравнения 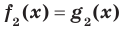 содержит множество корней уравнения
содержит множество корней уравнения 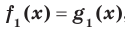 , то уравнение
, то уравнение 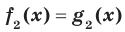 называют следствием уравнения
называют следствием уравнения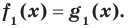
Например, уравнение 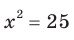 является следствием уравнения
является следствием уравнения 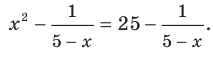 Убедитесь в этом самостоятельно. Также говорят, что из уравнения
Убедитесь в этом самостоятельно. Также говорят, что из уравнения 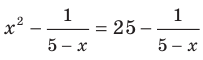 следует уравнение
следует уравнение 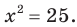 На рисунке 7.1 определение уравнения-следствия проиллюстрировано с помощью диаграммы Эйлера.
На рисунке 7.1 определение уравнения-следствия проиллюстрировано с помощью диаграммы Эйлера.
Еще одной причиной появления посторонних корней является то, что из равенства 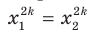 не обязательно следует равенство
не обязательно следует равенство 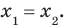 Например,
Например,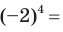
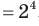 , но
, но 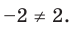 В то же время из равенства
В то же время из равенства 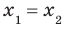 следует равенство
следует равенство 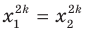
Справедлива следующая теорема.
Теорема 7.2. При возведении обеих частей уравнения в четную степень полученное уравнение является следствием данного.
Пример:
Решите уравнение 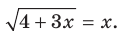
Решение:
Возведем обе части уравнения в квадрат. Получим уравнение, которое является следствием данного:
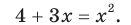 Отсюда
Отсюда 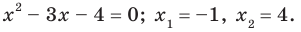 Проверка показывает, что число -1 — посторонний корень, а число 4 удовлетворяет данному уравнению. Ответ: 4.
Проверка показывает, что число -1 — посторонний корень, а число 4 удовлетворяет данному уравнению. Ответ: 4.
Пример:
Решите уравнение 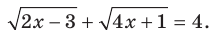
Решение:
Возведем обе части данного уравнения в квадрат:
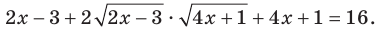 Отсюда
Отсюда 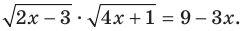 Переходя к уравнению-следствию, получаем:
Переходя к уравнению-следствию, получаем:
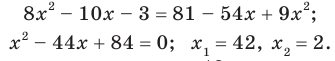 Проверка показывает, что число 42 является посторонним кор нем, а число 2 удовлетворяет данному уравнению. Ответ: 2.
Проверка показывает, что число 42 является посторонним кор нем, а число 2 удовлетворяет данному уравнению. Ответ: 2.
Пример:
Решите уравнение 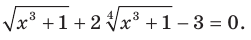
Решение:
Пусть 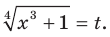 Тогда
Тогда 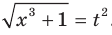 Теперь исходное уравнение принимает вид
Теперь исходное уравнение принимает вид
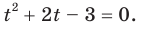 Отсюда t = -3 или t = 1. В случае, когда t = -3, получаем уравнение
Отсюда t = -3 или t = 1. В случае, когда t = -3, получаем уравнение 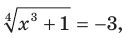 не имеющее решений. В случае, когда t = 1, получаем уравнение
не имеющее решений. В случае, когда t = 1, получаем уравнение 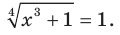 Завершите решение самостоятельно. Ответ: 0.
Завершите решение самостоятельно. Ответ: 0.
Напомним, что с методом, использованным при решении последнего уравнения, вы знакомы еще из курса алгебры 8-9 классов. Этот метод называют методом замены переменной.
ГЛАВНОЕ В ПАРАГРАФЕ 1
Наименьшее и наибольшее значения функции
Если для всех 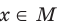 выполняется неравенство
выполняется неравенство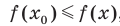 где
где 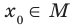 , то число
, то число 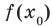 называют наименьшим значением функции
называют наименьшим значением функции 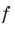 на множестве М и записывают:
на множестве М и записывают: 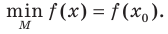
Если для всех 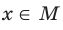 выполняется неравенство
выполняется неравенство 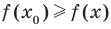 , где
, где 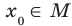 , то число
, то число 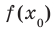 называют наибольшим значением функции f на множестве М и записывают:
называют наибольшим значением функции f на множестве М и записывают: 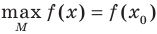 .
.
Четная и нечетная функции
Функцию 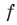 называют четной, если для любого
называют четной, если для любого 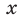 из области определения выполняется равенство
из области определения выполняется равенство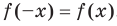 .
.
Функцию 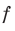 называют нечетной, если для любого х из области определения выполняется равенство
называют нечетной, если для любого х из области определения выполняется равенство 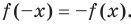
Ось ординат является осью симметрии графика четной функции. Начало координат является центром симметрии графика нечетной функции.
Корень 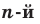 степени
степени
Корнем 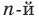 степени из числа
степени из числа 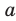 , где
, где 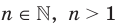 , называют такое число,
, называют такое число, 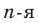 степень которого равна
степень которого равна 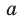 . Арифметическим корнем
. Арифметическим корнем 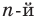 степени из неотрицательного числа
степени из неотрицательного числа 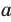 , где
, где 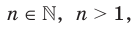 называют такое неотрицательное число,
называют такое неотрицательное число, 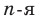 степень которого равна
степень которого равна 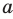 .
.
Для любого 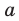 и
и 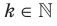 выполняются равенства:
выполняются равенства: 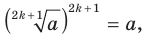
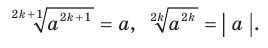
Для любого  выполняется равенство
выполняется равенство 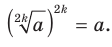
- Если
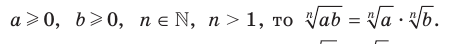
- Если
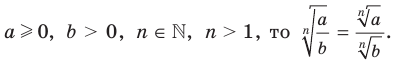 .
. - Если
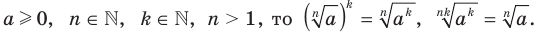
- Если
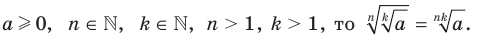
Степень с рациональным показателем
Степенью положительного числа 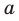 с показателем
с показателем 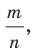 где
где 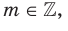
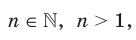 называют число
называют число 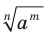 , то есть
, то есть 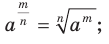
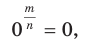 где
где 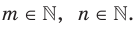
Функцию, которую можно задать формулой 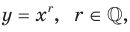 называют степенной функцией с рациональным показателем.
называют степенной функцией с рациональным показателем.
Для любого а > 0 и любых рациональных чисел р и q выполняются равенства: 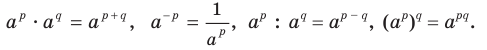 Для любых
Для любых 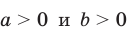 и любого рационального числа р выполняются равенства:
и любого рационального числа р выполняются равенства: 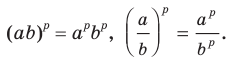
Иррациональные уравнения
Уравнения, содержащие переменную под знаком корня, называют иррациональными.
Если обе части уравнения возвести в нечетную степень, то получим уравнение, равносильное данному.
При возведении обеих частей уравнения в четную степень полученное уравнение является следствием данного.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |