
Формулы сокращенного умножения с примерами решения
Содержание:
Формулы сокращенного умножения
Умножение разности двух выражений на их сумму
Умножим разность 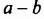
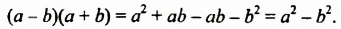
Итак,
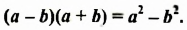
Полученное тождество позволяет умножать разность двух выражений на их сумму не по правилу умножения двух многочленов, а сокращенно: сразу записывать произведение в виде 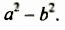 Поэтому доказанное тождество называют формулой сокращенного умножения. Формулируют се так:
Поэтому доказанное тождество называют формулой сокращенного умножения. Формулируют се так:
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Умножим по этому правилу разность 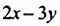 на сумму
на сумму 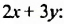
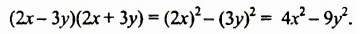
Из переместительного свойства умножения следует, что произведение суммы двух выражений и их разности равно разности квадратов этих выражений:
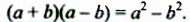
Примеры выполнения заданий:
Пример №135
Выполнить умножение:
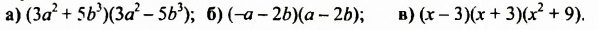
Решение:
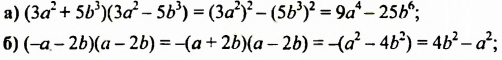
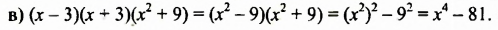
Пример №136
Вычислить 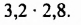
Решение:
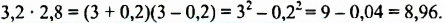
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений
Возведем в квадрат сумму 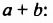
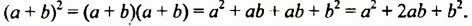
Итак,
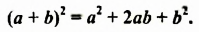
Полученное тождество называют формулой квадрата суммы. Оно является формулой сокращенного умножения, поскольку позволяет возводить в квадрат сумму любых двух выражений не по правилу умножения двух многочленов, а сокращенно: сразу записывать квадрат в виде трехчлена 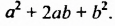
Формулируют формулу квадрата суммы так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение этих выражений плюс квадрат второго выражения.
Возведем в квадрат сумму 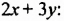
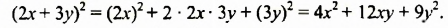
При возведении суммы 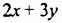 в квадрат промежуточные преобразования можно выполнять устно:
в квадрат промежуточные преобразования можно выполнять устно:
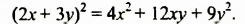
Квадрат разности двух выражений
Возведем в квадрат разность 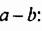
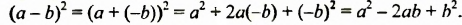
Итак, получили такую формулу квадрата разности:
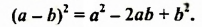
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения.
Квадрат суммы и квадрат разности двух выражений еще называют квадратом двучлена.
Квадраты противоположных чисел равны: 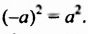 Поэтому при возведении в квадрат выражений
Поэтому при возведении в квадрат выражений 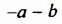 и
и 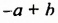 можно пользоваться формулами:
можно пользоваться формулами:
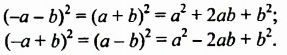
Для тех, кто хочет знать больше
Чтобы возвести сумму или разность двух выражений в куб, можно использовать формулы куба суммы или куба разности:
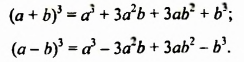
Докажем эти формулы.
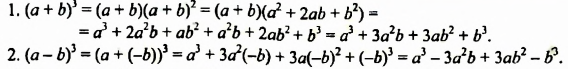
Формулируют формулу куба суммы так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения.
Формулу куба разности формулируют аналогично.
Примеры выполнения заданий:
Пример №137
Возвести в квадрат выражение:

Решение:
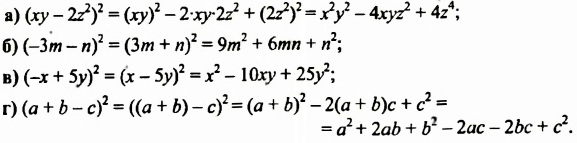
Разложение на множители разности квадратов двух выражений
В тождестве 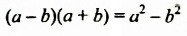 поменяем местами левую и правую части:
поменяем местами левую и правую части:
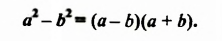
Полученное тождество называют формулой разности квадратов двух выражений. Формулируют ее так:
Разность квадратов двух выражении равна произведению разности этих выражений и их суммы.
Формула разности квадратов позволяет разложить на множители двучлена 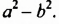 Ее можно использовать при разложении на множители разности квадратов любых двух выражений. Например:
Ее можно использовать при разложении на множители разности квадратов любых двух выражений. Например:
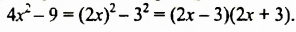
Сравните

Примеры выполнения заданий:
Пример №138
Разложить на множители:

Решение:
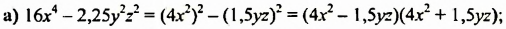
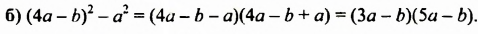
Пример №139
Вычислить 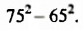
Решение:
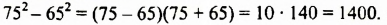
Пример №140
Решить уравнение 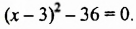
Решение:
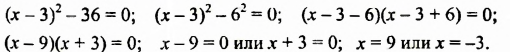
Ответ. 9; -3.
Разложение многочленов на множители с использованием формул квадрата суммы и квадрата разности
Запишем формулы квадрата суммы и квадрата разности двух выражений (квадрата двучлена), поменяв в них левые и правые части:
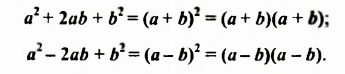
Первая из этих формул дает разложение на множители трехчлена 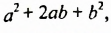 а вторая — трехчлена
а вторая — трехчлена 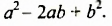
Примеры выполнения заданий:
Пример №141
Разложить на множители трехчлен 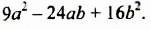
Решение:
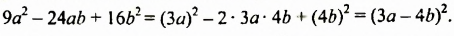
Пример №142
Найти значение выражения 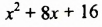 при
при 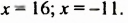
Решение:
Запишем сначала трехчлен 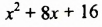 в виде квадрата двучлена:
в виде квадрата двучлена:
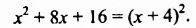
При 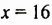 получим:
получим: 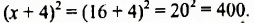
При 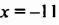 получим:
получим: 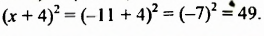
Разность и сумма кубов двух выражений
Разность квадратов двух выражений можно разложить на множители по формуле разности квадратов. При разложении на множители разности кубов двух выражений используют формулу разности кубов:
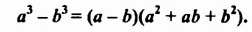
Докажем это тождество, перемножив выражения 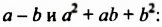
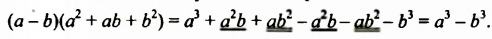
В формуле разности кубов трехчлен 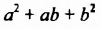 называют неполным квадратом суммы выражений
называют неполным квадратом суммы выражений 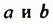 (он напоминает трехчлен
(он напоминает трехчлен 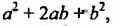 который является «полным» квадратом суммы выражений
который является «полным» квадратом суммы выражений 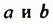 ). Поэтому формулу разности кубов можно сформулировать так:
). Поэтому формулу разности кубов можно сформулировать так:
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
При разложении на множители суммы кубов двух выражений используют формулу суммы кубов:
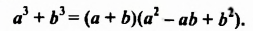
Докажем это тождество:
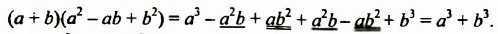
Трехчлен 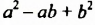 называют неполным квадратом разности выражений
называют неполным квадратом разности выражений 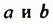 . Следовательно,
. Следовательно,
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Примеры выполнения заданий:
Пример №143
Разложить на множители:
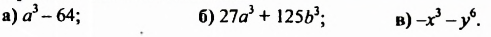
Решение:
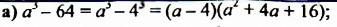
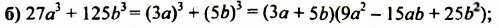
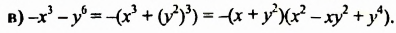
Применение нескольких способов для разложения многочленов на множители
Часто при разложении многочлена на множители нужно использовать несколько способов. Если это возможно, то разложение уместно начинать с вынесения общего множителя за скобки.
Рассмотрим несколько примеров:
1. Разложим на множители многочлен 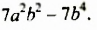
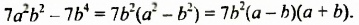
Сначала вынесли общий множитель 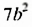 за скобки, а потом применили формулу разности квадратов.
за скобки, а потом применили формулу разности квадратов.
2. Разложим на множители многочлен 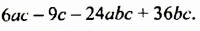
Все члены многочлена имеют общий множитель 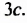 Вынесем eго за скобки:
Вынесем eго за скобки:
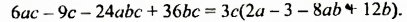
Многочлен 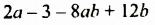 разложим на множители способом группировки:
разложим на множители способом группировки:
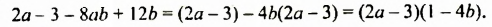
Таким образом,
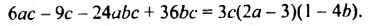
Примеры выполнения заданий:
Пример №144
Разложить на множители трехчлен:

Решение:
а) Если к выражению 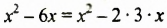 прибавить
прибавить 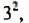 то есть 9, то получим выражение
то есть 9, то получим выражение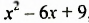 , которое является квадратом двучлена
, которое является квадратом двучлена 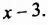
Поэтому, выделив квадрат этого двучлена, получим:
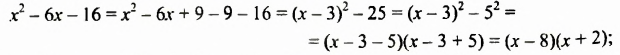
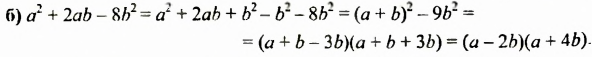
Пример №145
Разложить на множители многочлен 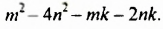
Решение:
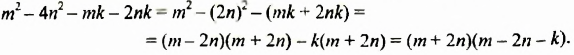
Пример №146
Решить уравнение 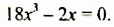
Решение:
Разложим левую часть уравнения на множители:
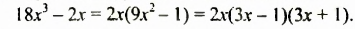
Получим уравнение
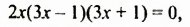
откуда: 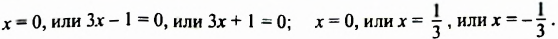
Ответ: 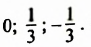
Применение преобразований выражений
Нам уже встречались задачи, при решении которых нужно было преобразовывать то или иное выражение. Чаще всего мы использовали преобразования выражений при решении уравнений, доказательстве тождеств, нахождении значений выражении. Рассмотрим еще некоторые задачи, решение которых связано с преобразованием выражений.
Сравнение значений многочлена с нулем
Пример №147
Доказать, что многочлен 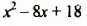 принимает только положительные значения.
принимает только положительные значения.
Решение:
Выделив из трехчлена 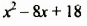 квадрат двучлена, получим:
квадрат двучлена, получим:
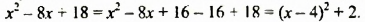
Мы представили многочлен в виде суммы двух слагаемых 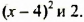 Слагаемое
Слагаемое 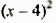 : при любых
: при любых 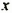 принимает только неотрицательные значения, слагаемое 2 — положительно. Поэтому выражение
принимает только неотрицательные значения, слагаемое 2 — положительно. Поэтому выражение 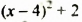 принимает только положительные значения. Поскольку
принимает только положительные значения. Поскольку 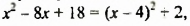 то и выражение
то и выражение 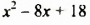 принимает только положительные значения.
принимает только положительные значения.
Нахождение наибольшего и наименьшего значений выражений
Исходя из равенства 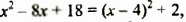 полученного в примере 1, можно
полученного в примере 1, можно
указать наименьшее значение многочлена 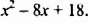 Оно равно
Оно равно 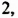 причем это наименьшее значение многочлен принимает при
причем это наименьшее значение многочлен принимает при 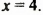
Пример №148
Найти наибольшее значение многочлена 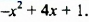
Решение:
Преобразуем данный многочлен так:
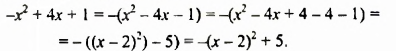
Наибольшее значение многочлена равно 5.
Решение задач на делимость
Пример №149
Доказать, что значение выражения 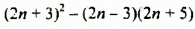 делится на 8 при любом целом значении
делится на 8 при любом целом значении 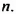
Решение:
Упростим данное выражение:
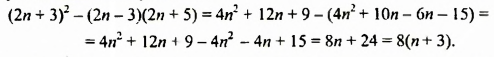
При любом целом значении 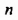 произведение
произведение 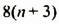 делится на 8, поэтому и значение выражения
делится на 8, поэтому и значение выражения 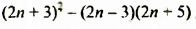 делится на 8.
делится на 8.
Нахождение значений многочлена с помощью микрокалькулятора
Пример №150
С помощью микрокалькулятора найти значение многочлена
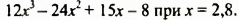
Решение:
Значение данного многочлена искать удобнее, если его предварительно преобразовать так:
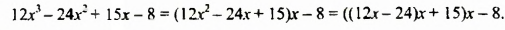 При
При 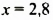 схема вычислений имеет вид:
схема вычислений имеет вид:

Выполнив вычисления, найдем значение многочлена. Оно равно 109,264.
Интересно знать
Античные математики использовали формулы сокращенного умножения задолго до нашей эры. В те времена формулы представлялись не в привычном нам символическом виде, а формулировались словами.
Ученые Древней Греции алгебраические утверждения, формулы, выражающие определенные зависимости между величинами, трактовали геометрически. Так, произведение 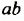 они рассматривали как площадь прямоугольника со сторонами
они рассматривали как площадь прямоугольника со сторонами 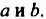
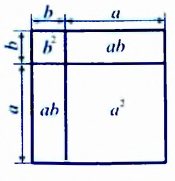
Приведем пример алгебраического утверждения, которое было известно древнегреческим ученым и в геометрической терминологии формулировалось так: площадь квадрата, построенного на сумме двух отрезков, равна сумме площади квадратов, построенных на каждом из этих отрезков, плюс удвоенная площадь прямоугольника, построенного на этих отрезках.
Нетрудно догадаться, что речь идет о формуле квадрата суммы, которую мы символически записываем так:
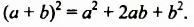
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |