
Формулы приведения с примерами решения
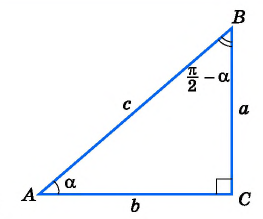
При изучении геометрии вы установили, что
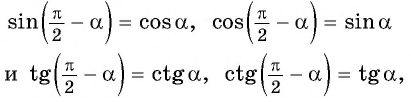
если 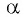
Свойство периодичности тригонометрических функций позволяет свести вычисление значений синуса, косинуса, тангенса и котангенса произвольного угла к вычислению значений этих функций при значениях аргумента, принадлежащих промежутку 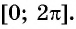 Например,
Например,
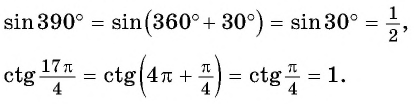
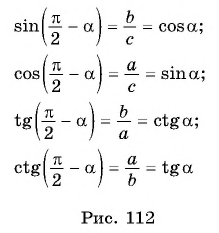
На практике принято сводить значения тригонометрических функций произвольного угла к вычислению значений этих функций для угла, принадлежащего промежутку 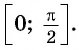 .
.
Это можно делать с помощью формул приведения.
Рассмотрим промежуток 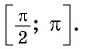 Любое число
Любое число 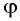 из этого промежутка можно пред ставить в виде
из этого промежутка можно пред ставить в виде 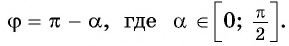
Например, 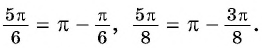
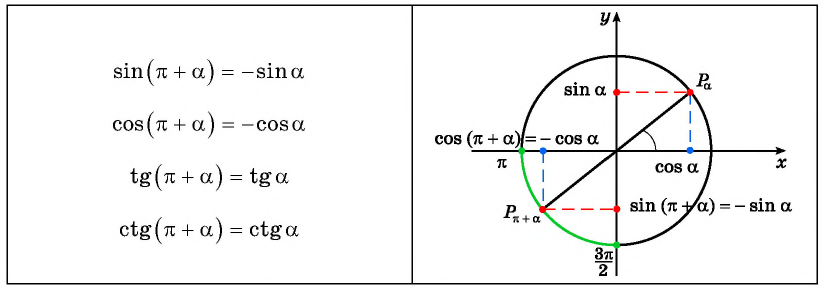
Поскольку ординаты точек 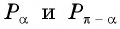 равны, а абсциссы отличаются только знаком, то:
равны, а абсциссы отличаются только знаком, то: 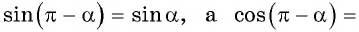
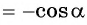 (рис. 113).
(рис. 113).
Тогда для 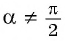 получим, что
получим, что 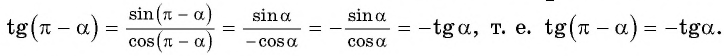
А для 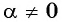 имеем:
имеем:
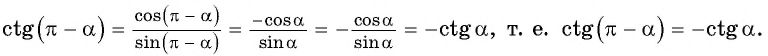
Вместе с тем любое число 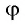 из промежутка
из промежутка 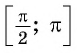 можно также представить в виде
можно также представить в виде 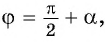 где
где 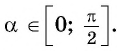 Например,
Например, 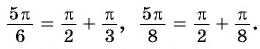
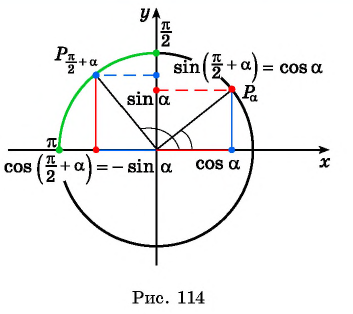
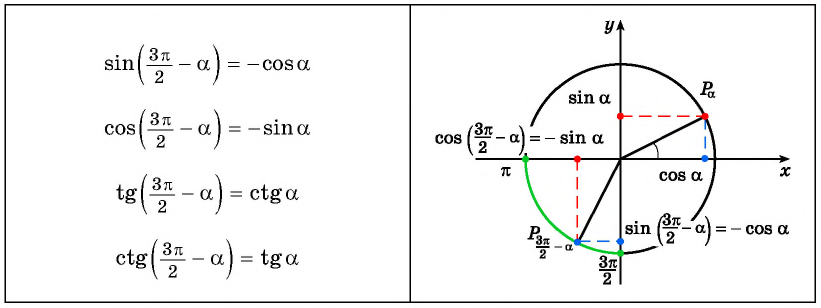
Так как ордината точки 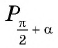 равна абсциссе точки
равна абсциссе точки 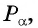 а абсцисса точки
а абсцисса точки 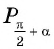 отличается от ординаты точки
отличается от ординаты точки 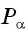 только знаком (рис. 114), то:
только знаком (рис. 114), то: 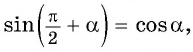 а
а 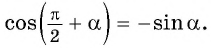
Для 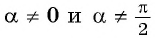 получим:
получим:
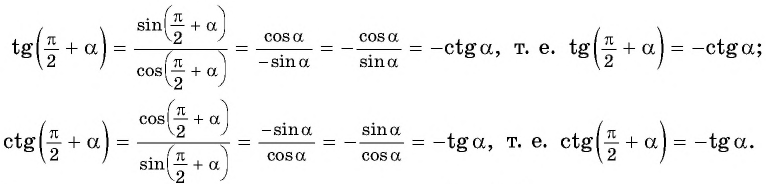
Так как любое число 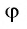 из промежутка
из промежутка 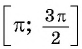 можно представить в виде
можно представить в виде 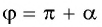 или
или 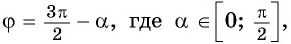 то, рассуждая аналогично, получим формулы приведения:
то, рассуждая аналогично, получим формулы приведения:
Поскольку любое число 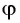 из промежутка
из промежутка 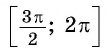 можно представить в виде
можно представить в виде 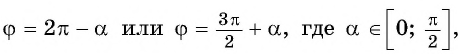 то получим:
то получим:
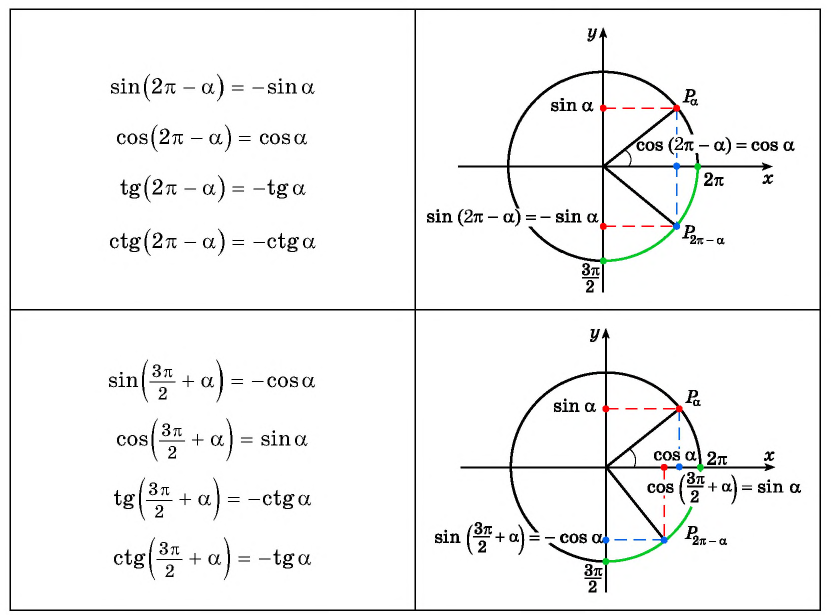
Проанализировав полученные формулы, можно заметить закономерности, позволяющие сформулировать правило, с помощью которого можно применять формулы приведения, не заучивая их:
В правой части формулы приведения ставится тот знак, который имеет в соответствующей четверти исходная функция, если считать, что угол 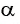 — острый.
— острый.
Если в формуле приведения аргумент имеет вид:
-
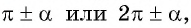 то название функции не меняется;
то название функции не меняется; -
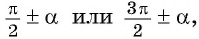 то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
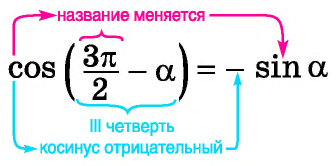
Например, применим полученное правило для выражения 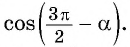
- Если считать, что угол
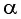 — острый, то —
— острый, то — 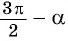 — угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус». - Поскольку аргумент имеет вид
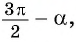 то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
то название функции «косинус» нужно поменять на «синус». Таким образом, получим: 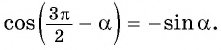
Пример:
Приведите выражение к тригонометрической функции числа 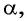 применив формулы приведения:
применив формулы приведения:
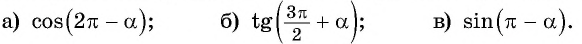
Решение:
Применим правило:
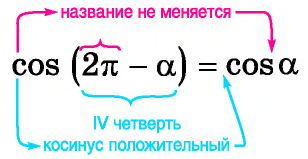
а) 1. Так как 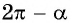 — угол четвертой четверти, в которой косинус положительный, то в правой части равенства не нужно ставить знак «минус».
— угол четвертой четверти, в которой косинус положительный, то в правой части равенства не нужно ставить знак «минус».
2. Поскольку аргумент имеет вид 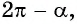 то название функции «косинус» не меняется. Значит,
то название функции «косинус» не меняется. Значит, 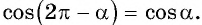
б) 1. Так как 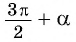 — угол четвертой четверти, в которой тангенс отрицательный, то в правой части равенства нужно поставить знак «минус».
— угол четвертой четверти, в которой тангенс отрицательный, то в правой части равенства нужно поставить знак «минус».
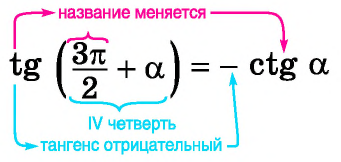
2.Поскольку аргумент имеет вид 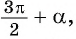 название функции «тангенс» нужно поменять на «котангенс». Тогда
название функции «тангенс» нужно поменять на «котангенс». Тогда 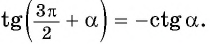
в) 1. Так как 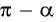 — угол второй четверти, в которой синус положительный, то в правой части равенства части равенства не нужно ставить знак «минус»
— угол второй четверти, в которой синус положительный, то в правой части равенства части равенства не нужно ставить знак «минус»
2. Поскольку аргумент имеет вид 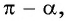 то название функции «синус» не меняется. Значит,
то название функции «синус» не меняется. Значит, 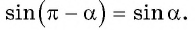

Пример:
Используйте формулы приведения и найдите значение выражения:
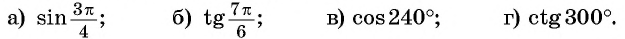
Решение:
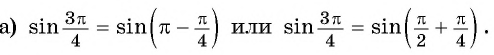
Первый способ:
- Так как
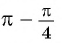 угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус». - Поскольку аргумент имеет вид
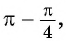 то название функции «синус» не меняется. Значит,
то название функции «синус» не меняется. Значит, 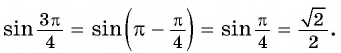
Второй способ:

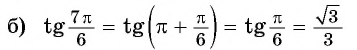 (в третьей четверти тангенс положительный, название функции не меняется).
(в третьей четверти тангенс положительный, название функции не меняется).
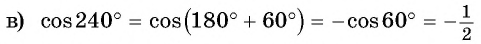 (в третьей четверти косинус отрицательный, название функции не меняется).
(в третьей четверти косинус отрицательный, название функции не меняется).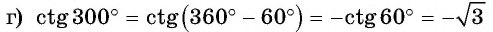 (в четвертой четверти котангенс отрицательный, название функции не меняется).
(в четвертой четверти котангенс отрицательный, название функции не меняется).
Пример:
Вычислите, используя формулы приведения:

Решение:
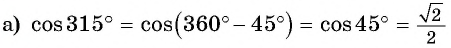 (в четвертой четверти косинус положительный, название функции не меняется);
(в четвертой четверти косинус положительный, название функции не меняется);
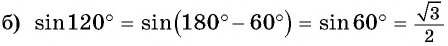 (во второй четверти синус положительный, название функции не меняется);
(во второй четверти синус положительный, название функции не меняется);
 (в третьей четверти котангенс положительный, название функции меняется);
(в третьей четверти котангенс положительный, название функции меняется);
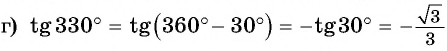 (в четвертой четверти тангенс отрицательный, название функции не меняется).
(в четвертой четверти тангенс отрицательный, название функции не меняется).
Пример:
Найдите значение выражения:
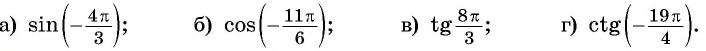
Решение:
а) Так как синус — нечетная функция, то
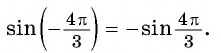
Применим формулы приведения:
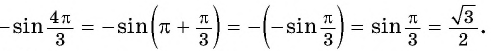
б) Воспользуемся свойством четности косинуса и получим:
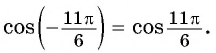
По формулам приведения: 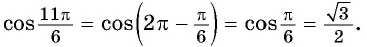
в) Воспользуемся свойством периодичности тангенса и получим:
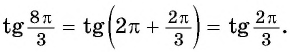
Применим формулы приведения: 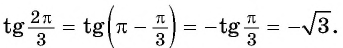
г) Поскольку котангенс — нечетная функция, то 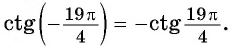
Используем свойство периодичности котангенса и получим:
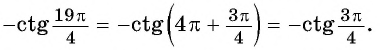
Пример:
По формулам приведения:
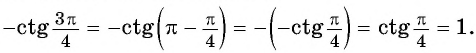
Приведите к тригонометрической функции угла 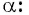
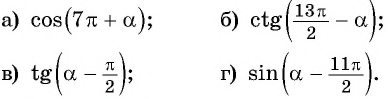
Решение:
а) Используем свойство периодичности косинуса и получим: 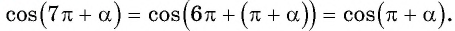
По формулам приведения: 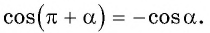
б) Воспользуемся свойством периодичности котангенса: 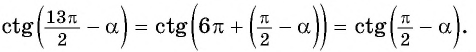
Применим формулы приведения: 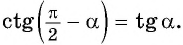
в) Так как тангенс — нечетная функция, то 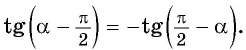 По формулам приведения:
По формулам приведения: 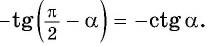
г) Поскольку синус — нечетная функция, то
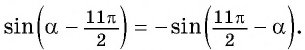
Воспользуемся свойством периодичности синуса и получим:
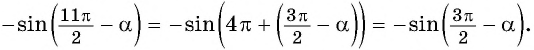
По формулам приведения: 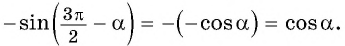
Пример:
Приведите к тригонометрической функции угла 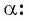

Решение:
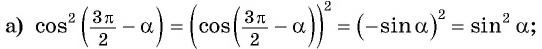
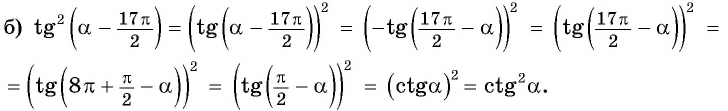
Пример:
Вычислите:

Решение:
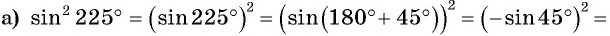
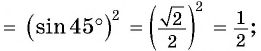
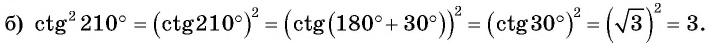
Пример:
Упростите выражение:
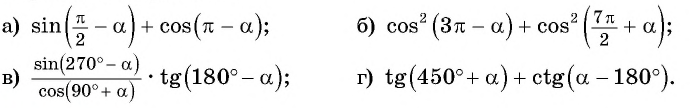
Решение:
а) Применим формулы приведения: 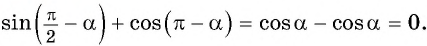
б)Воспользуемся периодичностью косинуса и формулами приведения и получим:
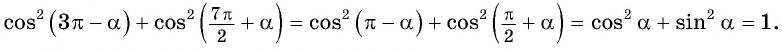
в)Применим формулы приведения:
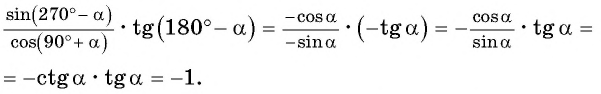
г) Используем периодичность тангенса, нечетность котангенса и формулы приведения:
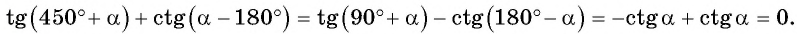
Пример:
Решите уравнение: 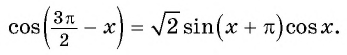
Решение:
Применим формулы приведения и получим:
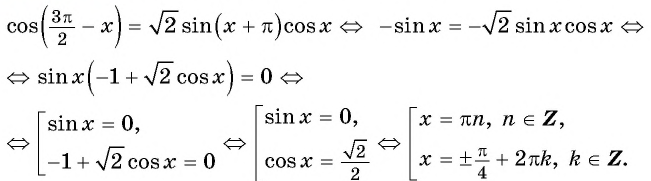
Ответ: 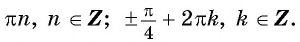
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Функции y=tg x и y=ctg x - их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства