
Формулы преобразования суммы и разности синусов (косинусов) в произведение
Формулы синуса суммы и разности двух углов можно использовать для получения новых формул, необходимых для решения уравнений, изучения свойств функций и т. п.
Например, решим уравнение 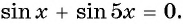
Для решения данного уравнения сумму 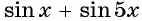
Выведем формулу, преобразующую сумму синусов в произведение.
Сложим почленно два равенства:
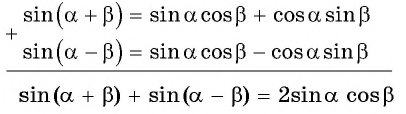
Обозначим 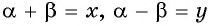 и решим систему уравнений
и решим систему уравнений 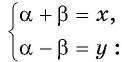
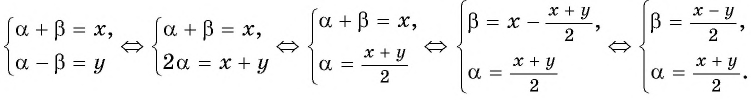
Подставим выражения для 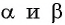 в равенство
в равенство 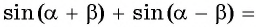
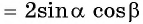 и получим формулу суммы синусов двух углов:
и получим формулу суммы синусов двух углов: 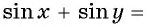
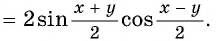
Вернемся к решению уравнения 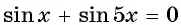 и применим формулу суммы синусов:
и применим формулу суммы синусов: 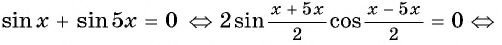
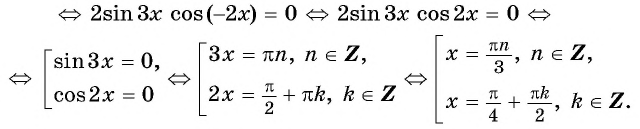
Ответ: 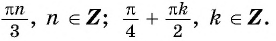
Вычтя из равенства 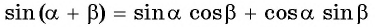 равенство
равенство 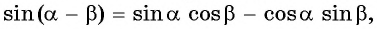 можно получить формулу разности синусов двух углов:
можно получить формулу разности синусов двух углов: 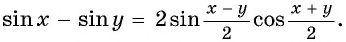
Аналогично, с помощью равенств 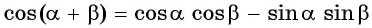 и
и 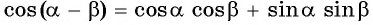 можно получить формулы
можно получить формулы
- суммы косинусов двух углов:
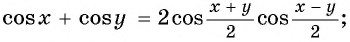
- разности косинусов двух углов:
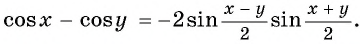
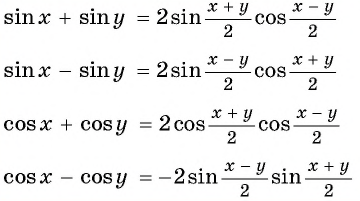
Пример:
Представьте в виде произведения:
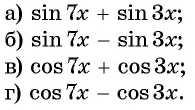
Решение:
Применим формулы преобразования суммы и разности в произведение и получим:
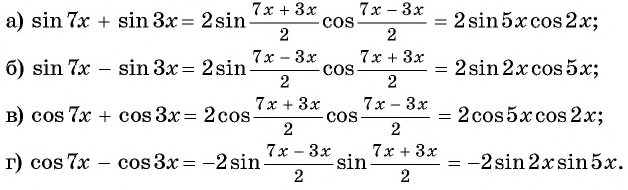
Пример:
Сократите дробь 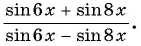
Решение:
Применим формулы суммы и разности синусов двух углов: 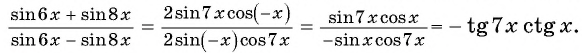
Пример:
Найдите значение выражения 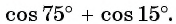
Решение:
Применим формулу суммы косинусов:
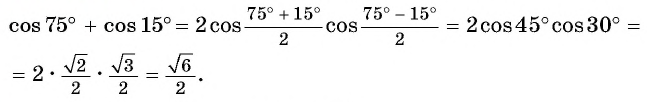
Пример:
Докажите тождество 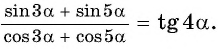
Решение:
Воспользуемся формулами суммы синусов и суммы косинусов двух углов:
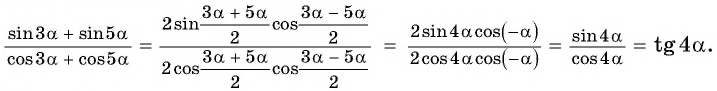
Пример:
Вычислите:

Решение:

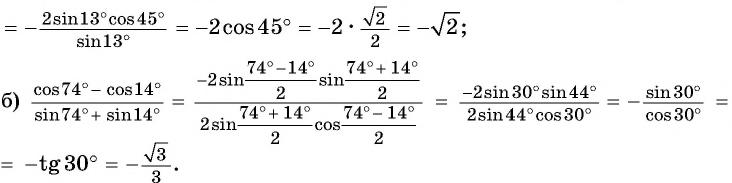
Пример:
Решите уравнение:
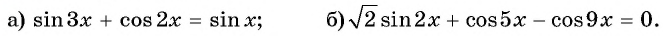
Решение:
а) Запишем уравнение в виде 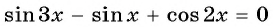 и применим формулу разности синусов:
и применим формулу разности синусов:
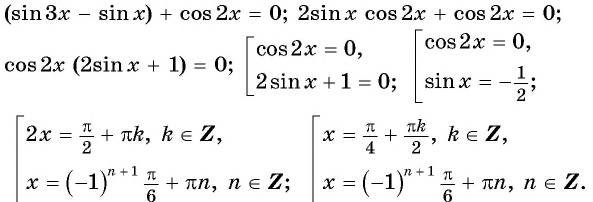
Ответ: 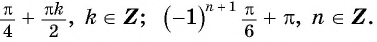
б) Воспользуемся формулой разности косинусов и получим:
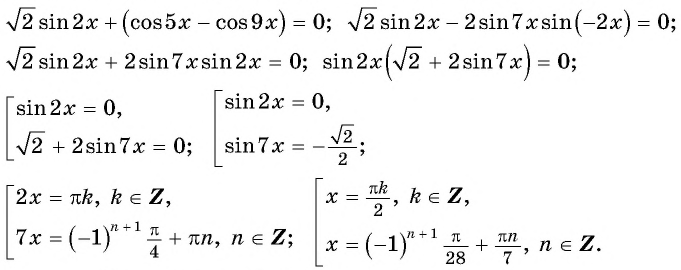
Ответ: 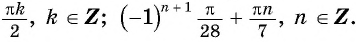
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |