
Формула Тейлора и ее применение с примерами решения
Содержание:
Формула Тейлора и ее применение
Формула Тейлора
Теорема: Если функция 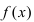
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора 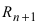 называется остаточным членом, вид которого установил Лагранж:
называется остаточным членом, вид которого установил Лагранж: 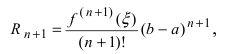 величина
величина 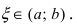
В этой формуле неизвестной является только величина 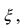 причем в указанном интервале согласно теореме Лагранжа такая точка всегда присутствует, хотя бы в единственном числе. Если зафиксировать начало интервала, а его конец считать переменной величиной, то формула Тейлора принимает вид:
причем в указанном интервале согласно теореме Лагранжа такая точка всегда присутствует, хотя бы в единственном числе. Если зафиксировать начало интервала, а его конец считать переменной величиной, то формула Тейлора принимает вид: 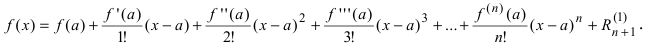
При a = 0 формула Тейлора переходит в формулу Маклoрена:
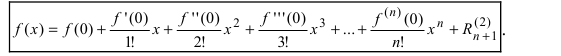
Пример:
Представить по формуле Маклорена функцию 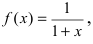 ограничившись n=2.
ограничившись n=2.
Решение:
Вычислим три первых производных заданной функции:
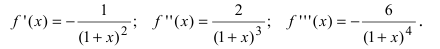 При х = 0 получим
При х = 0 получим 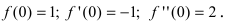 Остаточный член имеет вид
Остаточный член имеет вид 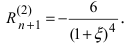 Следовательно, при n = 2 заданная функция по формуле Маклорена имеет вид:
Следовательно, при n = 2 заданная функция по формуле Маклорена имеет вид: 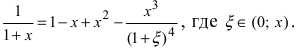 Отметим, что полученное выражение справедливо при
Отметим, что полученное выражение справедливо при 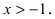 Решим найденное равенство относительно величины
Решим найденное равенство относительно величины 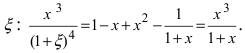 Отсюда получаем
Отсюда получаем 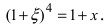 Следовательно,
Следовательно, 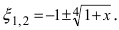 Так как выражение под радикалом 4-ой степени должно быть неотрицательным и
Так как выражение под радикалом 4-ой степени должно быть неотрицательным и 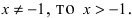 Таким образом, из двух корней теореме Тейлора удовлетворяет только корень
Таким образом, из двух корней теореме Тейлора удовлетворяет только корень 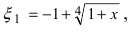 который действительно лежит между нулем и х.
который действительно лежит между нулем и х.
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:
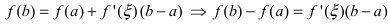 (см. теорему Лагранжа ТЗ Лекции №18). При n = 1 получаем
(см. теорему Лагранжа ТЗ Лекции №18). При n = 1 получаем 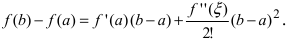 Если положить
Если положить 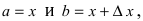 то получим формулу
то получим формулу
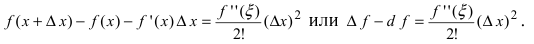
Применение формулы Тейлора
Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 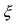 в остаточном члене в форме Лагранжа лежит в пределах от а до х.
в остаточном члене в форме Лагранжа лежит в пределах от а до х.
Пример:
Представить функцию 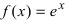 по формуле Маклорена.
по формуле Маклорена.
Решение:
Так как 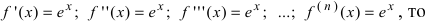
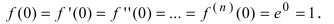 Следовательно,
Следовательно, 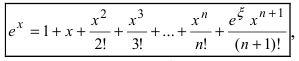 где
где 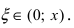 Отсюда следует,
Отсюда следует, 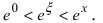
Пример:
Вычислить 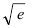 с точностью
с точностью 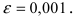
Решение:
Так как основание 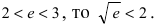 Следовательно, при х = 1/2 остаточный член равен
Следовательно, при х = 1/2 остаточный член равен 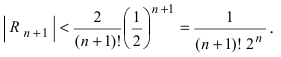 При n = 3: остаточный член
При n = 3: остаточный член 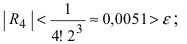
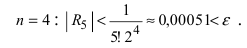 Следовательно, удерживая пять первых слагаемых в формуле Маклорена, получим с требуемой точностью, что
Следовательно, удерживая пять первых слагаемых в формуле Маклорена, получим с требуемой точностью, что 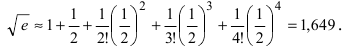
Пример:
Вычислить число е с точностью 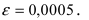
Решение:
Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа 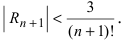
При n = 6 имеем 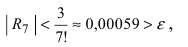
при n = 7 получаем 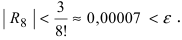
Итак, 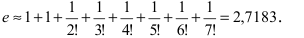
Если вычислять значение числа е с точностью 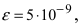 то потребуется взять 13 первых слагаемых, при этом
то потребуется взять 13 первых слагаемых, при этом 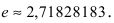 Аналогично формула Маклорена-Тейлора применяется для вычисления и других функций. Например, для вычисления натуральных логарифмов используется формула:
Аналогично формула Маклорена-Тейлора применяется для вычисления и других функций. Например, для вычисления натуральных логарифмов используется формула: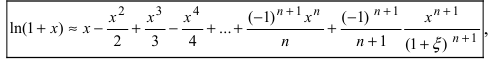 причем
причем 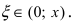
Пример:
Вычислить 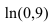 с точностью
с точностью 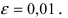
Решение:
В данном примере х = -0,1. Так как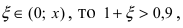 следовательно, остаточный член
следовательно, остаточный член 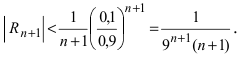 При n = 1 получаем
При n = 1 получаем 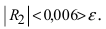 Следовательно, достаточно взять первый член в формуле Маклорена-Тейлора
Следовательно, достаточно взять первый член в формуле Маклорена-Тейлора 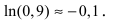
Формула тейлора
Пусть функция y=f(x) дифференцируема в точке 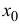 . Тогда (см. формулу (9.5)) ее приращение
. Тогда (см. формулу (9.5)) ее приращение 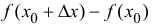
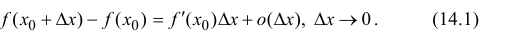
Пусть 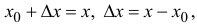 тогда (14.1) перепишется в виде
тогда (14.1) перепишется в виде 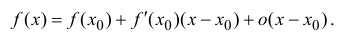
Рассмотрим многочлен 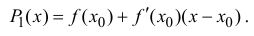
Многочлен 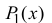 обладает следующими свойствами:
обладает следующими свойствами:
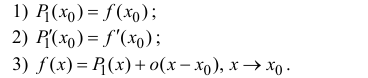
Пусть функция y=f(x) n раз дифференцируема в точке 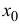 . Найдем многочлен
. Найдем многочлен
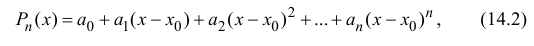
обладающий аналогичными свойствами:
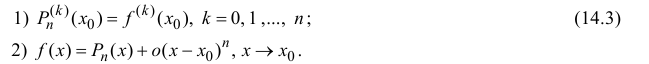
Из (14.2), (14.3) следует, что
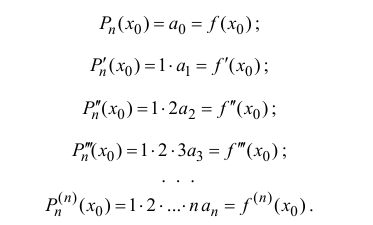
Поэтому коэффициенты 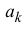 многочлена (14.2) задаются формулой
многочлена (14.2) задаются формулой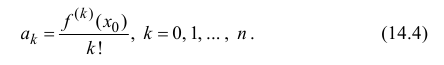
Далее

Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 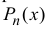 задаются формулами (14.4)). Тем самым теорема доказана.
задаются формулами (14.4)). Тем самым теорема доказана.
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке 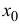 , тогда
, тогда
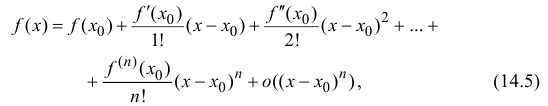
где 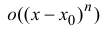 – бесконечно малая функция более высокого порядка
– бесконечно малая функция более высокого порядка
малости, чем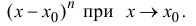
Формула (14.5) называется формулой Тейлора, многочлен
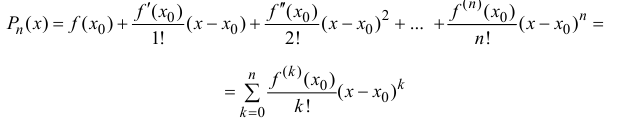
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности 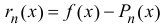 в виде
в виде 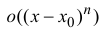 – остаточным членом в форме Пеано.
– остаточным членом в форме Пеано.
Если функция 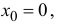 то (14.5) перепишется в виде
то (14.5) перепишется в виде
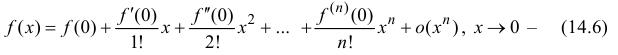
формула Маклорена.
Если функция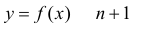 раз дифференцируема в некоторой окрестности
раз дифференцируема в некоторой окрестности
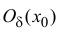 точки
точки 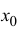 , то остаточный член
, то остаточный член 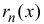 можно представить в виде
можно представить в виде
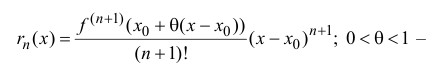 остаточный член в форме Лагранжа и формула
остаточный член в форме Лагранжа и формула
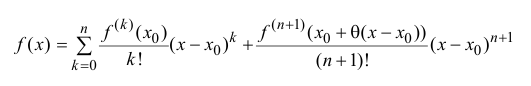
называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.
Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений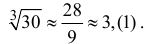
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа:
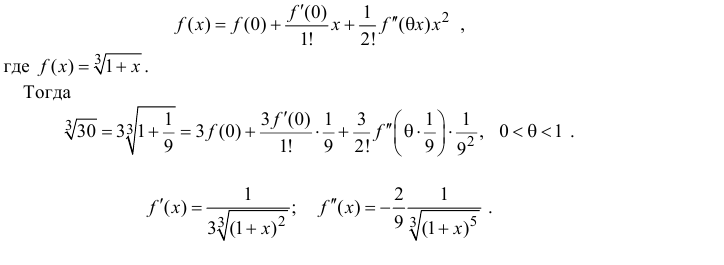
Поэтому
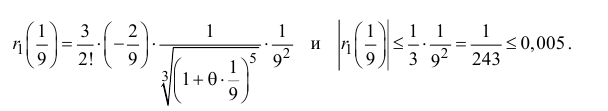
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.
Пример 14.2
Запишем формулу Маклорена n-го порядка для функции y=sin x:
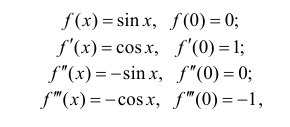
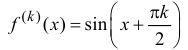 (см. упражнение 10.1)
(см. упражнение 10.1) 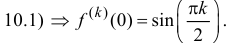
Таким образом, 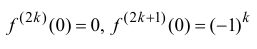 и по формуле (14.6)
и по формуле (14.6)
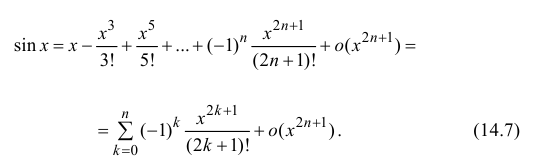
Аналогично
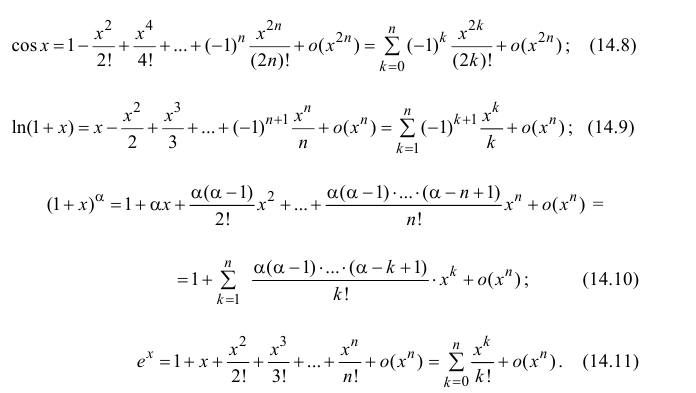
Формулы (14.7)–(14.11) называются основными разложениями.
Пример 14.3
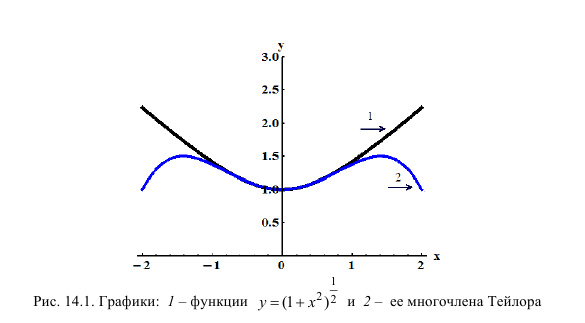
Разложить 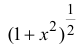 по формуле Маклорена до члена
по формуле Маклорена до члена 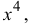 используя основные разложения. Оценить погрешность при
используя основные разложения. Оценить погрешность при 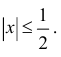
Решение
Пусть 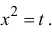 Тогда (см. формулу (14.10))
Тогда (см. формулу (14.10))
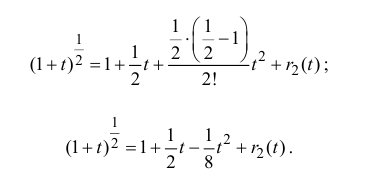
Остаточный член запишем в форме Лагранжа:
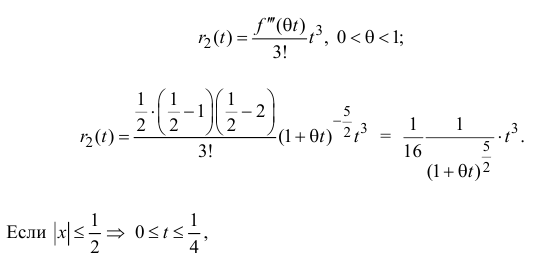
поэтому 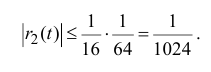
Таким образом, 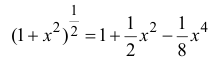 и погрешность при
и погрешность при 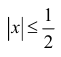 меньше чем
меньше чем
Пример 14.4
Найти 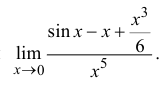
Решение
Воспользуемся разложением (14.7):
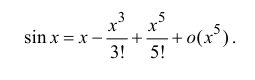
Тогда
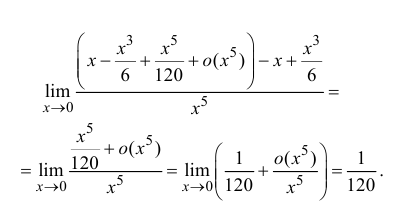
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных