Физический и математический маятники в физике - виды, формулы и определения с примерами

Физический и математический маятники:

Любое тело, у которого ось вращения не проходит через его центр масс, способно осуществлять колебания. Такие тела называются физическими маятниками. У тел правильной формы, например у плоских фигур, центр масс совпадает с их геометрическим центром (рис. 23).

Если такие тела вывести из состояния равновесия, они будут совершать колебания. Если бы в системе не было силы трения, такие колебания осуществлялись бы очень длительное время.

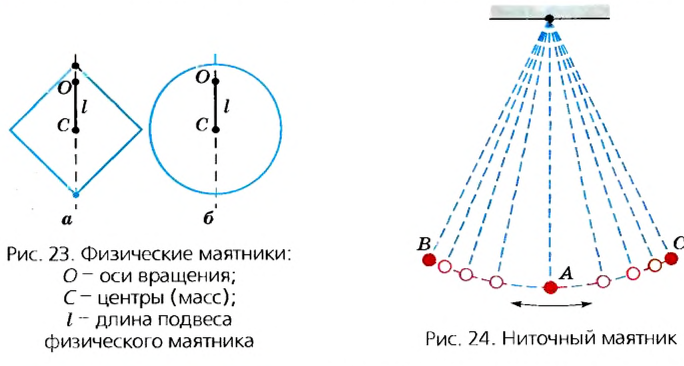
Простейшим маятником для исследований является так называемый ниточный маятник (рис. 24). Это шарик, подвешенный на нитке. Длиной такого маятника является расстояние от точки подвешивания нитки к центру шарика. Если такой шарик вывести из состояния равновесия (переместить в точку В или С), он будет совершать колебания по дуге окружности ВАС.

• Заказать решение задач по физике

Расстояние от оси вращения физического маятника к его центру масс

Понятно, такие колебания будут характеризоваться периодом Т и частотой f и могут иметь различную амплитуду.

Для упрощенного рассмотрения тех или иных явлений в науке часто пользуются идеальными моделями. Такой идеальной моделью является математический маятник.

Математический маятник - это точечное тело, подвешенное на нити, которая не растягивается и не имеет веса.

Понятно, что в природе нет ни точечных тел, ни нерастяжимых и невесомых нитей. Но во многих случаях ниточный маятник можно считать приближенным к математическому.