Фильтры и топологические методы анализа линейных электрических цепей

Содержание:

Электрические фильтры и топологические методы анализа линейных электрических цепей:

Изучая свойства резонансных цепей, мы встретились с понятием полосы пропускания колебательного контура. Было установлено, что чем выше добротность контура, тем уже его полоса пропускания и соответственно острее резонансная кривая. Острота резонансной кривой характеризует частотную избирательность колебательного контура, т. е. его способность пропускать или задерживать электрические колебания только определенной частоты — резонансной или близкой к ней.

Однако на практике встречается необходимость выделения не только одной какой-либо частоты, но целой полосы частот. Например, для передачи по радио разговора требуется отделить определенную полосу частот, в пределах которой ведется данная передача, от всех других частот. Такое разделение частот осуществляется с помощью электрических фильтров.

Электрический фильтр представляет собой пассивный четырехполюсник, пропускающий некоторую определенную полосу частот с малым затуханием; вне этой полосы частот затухание велико. Полоса частот, при которых затухание мало, называется полосой пропускания фильтра. Остальную область частот составляет полоса задерживания (илизатухания) фильтра.

Практическое применение электрических фильтров весьма широко и разнообразно. Они применяются не только в аппаратуре связи, но и в автоматике, приборостроении и других областях техники, где используется принцип разделения частот.

Система одновременного телеграфирования и телефонирования по одному и тому же проводу с использованием индуктивностей и емкостей для устранения влияния одного вида связи на другой была применена в России впервые в 1880 г. военным инженер-капитаном Г. Г. Игнатьевым, осуществившим разделение двух каналов связи (телефона и телеграфа) с помощью индуктивных катушек и конденсаторов.

Эти элементы, примененные в целях отделения полосы нижних частот от полосы верхних частот, являлись простейшим видом фильтрующих устройств.

Совершенствование электрических фильтров неразрывно связано с последующим развитием высокочастотной техники и электроники. Создание многоканальной проводной связи и радиосвязи сопровождалось разработкой теории электрических фильтров и методов их расчета и непрерывным совершенствованием самих фильтров. Теория электрических фильтров базируется на общей теории четырехполюсников.

Электрические фильтры могут быть классифицированы различным образом.

Классификация по пропускаемым частотам. В зависимости от пропускаемого спектра частот фильтры разделяются на фильтры: а) нижних частот (низкочастотные); б) верхних частот (высокочастотные); в) полосовые; г) заграждающие (режекторные).

Классификация по схемам звеньев. Фильтры могут состоять из звеньев Г-, Т-, П-образных, мостовых и др. В зависимости от числа звеньев фильтр может быть однозвенным или многозвенным.

Классификация фильтров по характеристикам. В отличие от простейших фильтров типа k различают фильтры более высокого класса — производные фильтры типа т и др. Смысл коэффициентов k и m будет пояснен ниже.

Классификация фильтров по типам элементов. Различают фильтры: а) реактивные (состоящие из элементов L и С); б) пьезоэлектрические (состоящие преимущественно из кварцевых пластин); в) безындуктивные (состоящие из элементов r и С) и др.

Условие пропускания реактивного фильтра

Наименьшее число элементов, из которых может состоять фильтр, равно двум (Г-образное звено). Фильтры, содержащие Т- и П-образные звенья, могут рассматриваться в качестве комбинаций, составленных из Г-образных звеньев.

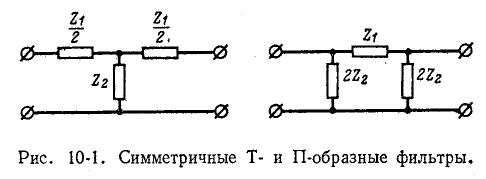
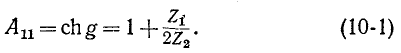
Мера передачи g симметричного Т- или П-образного фильтра может быть определена как удвоенная мера передачи g/2 Г-образного фильтра. Согласно (9-48)

Полосой пропускания реактивного фильтра является область частот, при которых собственное затухание реактивного фильтра равно нулю (а = 0).

Покажем, что четырехполюсник, состоящий из одних индуктивностей или одних емкостей (знаки 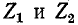одинаковы), не может иметь полосы пропускания. Иначе говоря, такой четырехполюсник не является фильтром. Действительно, пусть Г-образный или симметричный Т- или П-об-разный четырехполюсник состоит из чисто реактивных элементов, т. е.

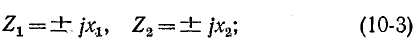
здесь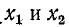— модули реактивных сопротивлений; положительные знаки относятся к индуктивным, отрицательные — к емкостным элементам.

Согласно (10-2)

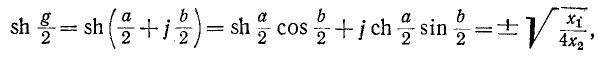
откуда, разделяя действительные и мнимые части, получаем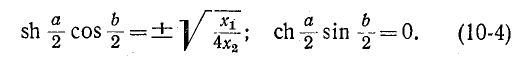

Ввиду того что гиперболический косинус действительного аргумента не может быть равен нулю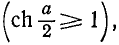 на основании (10-4)

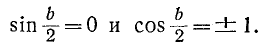
Таким образом, при одинаковом характере сопротивлений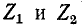 затухание фильтра определяется по формуле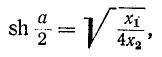

т. е. а > 0 (четырехполюсник не имеет полосы пропускания).

Четырехполюсник обладает свойствами фильтра только в том случае, когда сопротивления 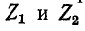имеют разные знаки, т. е.

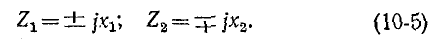
При этом 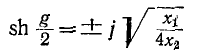и, следовательно,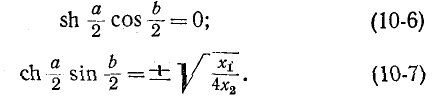

Уравнение (10-6) удовлетворяется при

или

Условие (10-8) соответствует полосе пропускания (а = 0). В этом случае 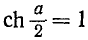и согласно (10-7)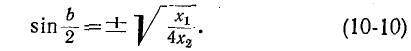

По такому закону изменяется коэффициент фазы фильтра в полосе пропускания 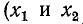зависят от частоты).

В свою очередь условие (10-9) соответствует полосе

задерживания. В этом случае 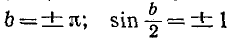и на основании (10-7)

По такому закону изменяется затухание фильтра в полосе задерживания. Формулы (10-10) и (10-11) справедливы для Г-образных и симметричных Т- и П-образных фильтров. При этом под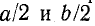 подразумеваются собственное затухание и коэффициент фазы каждого Г-образного звена. Т- или П-образный фильтр состоит из двух Г-образных звеньев, и поэтому его собственное затухание и коэффициент фазы равны соответственно а и b.

Для любого симметричного реактивного фильтра в полосе пропускания, т. е. при а — 0, выполняется условие

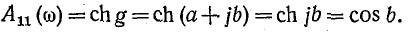
Поскольку косинус изменяется от — 1 до + 1,

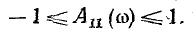
Это условие в случае Т- или П-образного фильтра принимает вид:

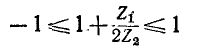
ИЛИ

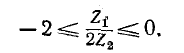
Разделив все части неравенства на 2, получим

Таким образом, предельные частоты, лежащие на границе полосы пропускания (так называемые частоты среза), удовлетворяют условиям:

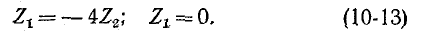
Неравенство (10-12) носит название условия пропускания реактивного фильтра (Г-, Т- или П-образ-ного).

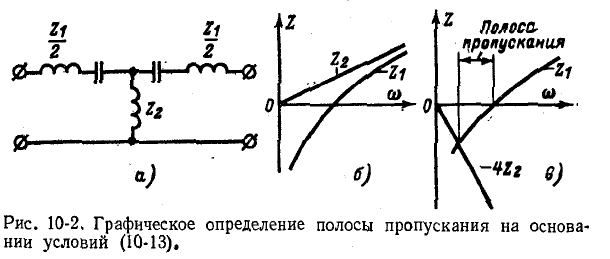
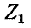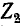Частоты среза находятся из уравнений (10-13) аналитически (если заданы функциональные выражения и  в зависимости от частоты) или графически (если заданы частотные характеристики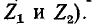

На рис. 10-2, б в виде примера показаны частотные характеристики 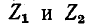фильтра, изображенного на рис.

10-2, а; полоса пропускания графически найдена на рис. 10-2, в.

Частоты среза могут быть также получены из рассмотрения частотной характеристики входного сопротивления фильтра, нагруженного согласованно, т. е. при помощи характеристического сопротивления фильтра.

В случае Т-образного фильтра характеристическое сопротивление

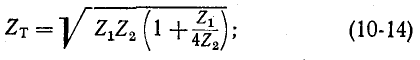
в случае П-образного фильтра    
  
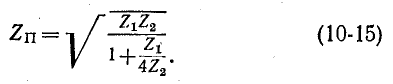
Как было доказано выше, условие а = 0 получено только при разных знаках 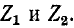 может быть . В этом случае
 
а произведение 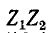— действительное число.  Выражения (10-14) и (10-15) получаются действительными при  

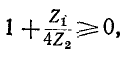
т. е. при    

Сопоставление (10-16) и (10-17) с (10-12) показывает, что условие, при котором характеристическое сопротивление рассматриваемого фильтра имеет действительное значение, совпадает с условием пропускания фильтра. Поэтому предельные частоты полосы, соответствующей действительным значениям характеристического сопротивления, являются частотами среза.

Физически это объясняется следующим образом. В полосе частот, при которых характеристическое сопротивление фильтра действительно, фильтр нагружен активным сопротивлением r, равным характеристическому по условиям согласованного включения.

Рассматриваемая здесь теория фильтров предполагает нагрузку фильтра согласованной, хотя в действительности согласовать нагрузку на всех частотах невозможно.

Мощность, потребляемая этой нагрузкой, является активной мощностью. Она равна

где 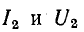— действующие ток и напряжение на выходе фильтра.

Входное сопротивление симметричного фильтра, нагруженного согласованно, в зоне пропускания также равно г, и поэтому мощность на входе фильтра равна:

здесь 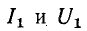— действующие ток и напряжение на входе фильтра.

Поскольку рассматривается идеальный фильтр, т. е. фильтр, состоящий из чисто реактивных элементов, активная мощность внутри фильтра не расходуется и поэтому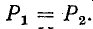

На основании (10-18) и (10-19) следует, что

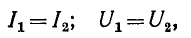
т. е. затухание равно нулю.

Итак, в полосе пропускания фильтр имеет активное характеристическое сопротивление. В полосе задерживания характеристическое сопротивление фильтра является реактивным.

Отсюда вытекает простой способ графического нахождения частот среза по частотным характеристикам входных сопротивлений холостого хода 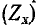и короткого замыкания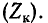

Характеристическое сопротивление 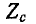фильтра связано с 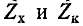формулой

Очевидно, что 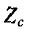будет действительным числом при разных знаках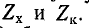

На рис. 10-3, б показаны кривые 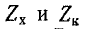для фильтра рис. 10-3, а. После перемножения 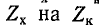и извлечения корня получается кривая рис. 10-3, в; полоса частот, в пределах которой 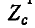имеет действительное значение, т. е.

представляет активное сопротивление, соответствует полосе пропускания фильтра х.

Очевидно, что эта полоса ограничена частотам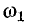и и 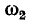(рис. 10-3, б)\ в пределах этой полосы 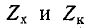имеют разные знаки. Вне этой полосы 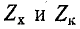имеют одинаковый

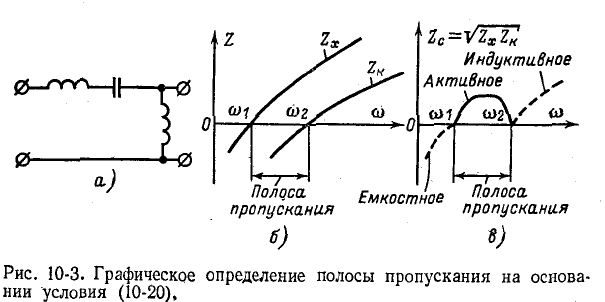
знак и, следовательно, характеристическое сопротивление в соответствии (с 10-20) имеет мнимые значения (реактивное сопротивление), показанные на рис. 10-3, в пунктиром.

Данное положение является общим для фильтров без потерь всех типов.

Фильтры типа k

Пусть составные элементы Г-образного звена являются взаимно обратными двухполюсниками. Это означает, что произведение их комплексных сопротивлений во всем диапазоне частот постоянно, т. е. не зависит от частоты:

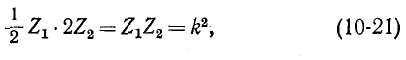
где k — действительное число.

Можно показать, что и произведение характеристических сопротивлений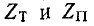 того же Г-образного звена также 

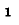По оси ординат откладывается или действительное, или мнимое значение характеристического сопротивления в зависимости от области частот,

равно 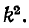Действительно, умножая (10-14) на (Ю-15), получаем:

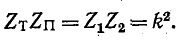
Фильтры, удовлетворяющие условию (10-21), получили название фильтров типа k .

С учетом (10-5) и (10-21) выражения (10-10)-—(10-12), (10-14) и (10-15) принимают вид

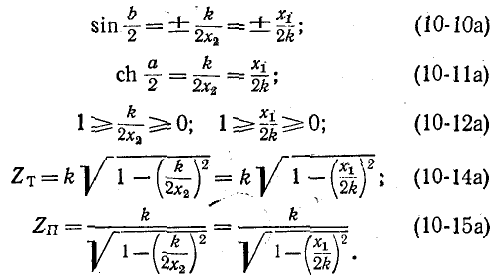
Таким образом, при заданном значении k достаточно воспользоваться только одной из частотных функци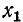й или 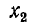(представленной аналитически или графически) для определения всех прочих характеристик фильтра типа k*.

Приведенные выше формулы справедливы для Г-, Т-и П-образных звеньев. Иначе говоря, при одних и тех же значениях k 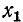и (или 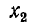) ширина полосы пропускания и характеристические сопротивления Г-образного фильтра получаются такими же, как и в случае Т- и П-образных фильтров. Разница заключается лишь в собственном затухании и коэффициенте фазы, которые при переходе от Г-образного звена к Т- или П-образному звену удваиваются.

На рис. 10-4—10-7 показаны схемы фильтров нижних частот, верхних частот, полосовых и заграждающих (для Г-, Т- и П-образных звеньев).

Физическое действие таких фильтров легко объяснить тем, что на низких частотах индуктивные сопротивления малы, а емкостные велики; на высоких же частотах имеет

* В расчетах коэффициент k выбирается из условия согласования сопротивления нагрузки с характеристическим сопротивлением фильтра при определенной частоте.

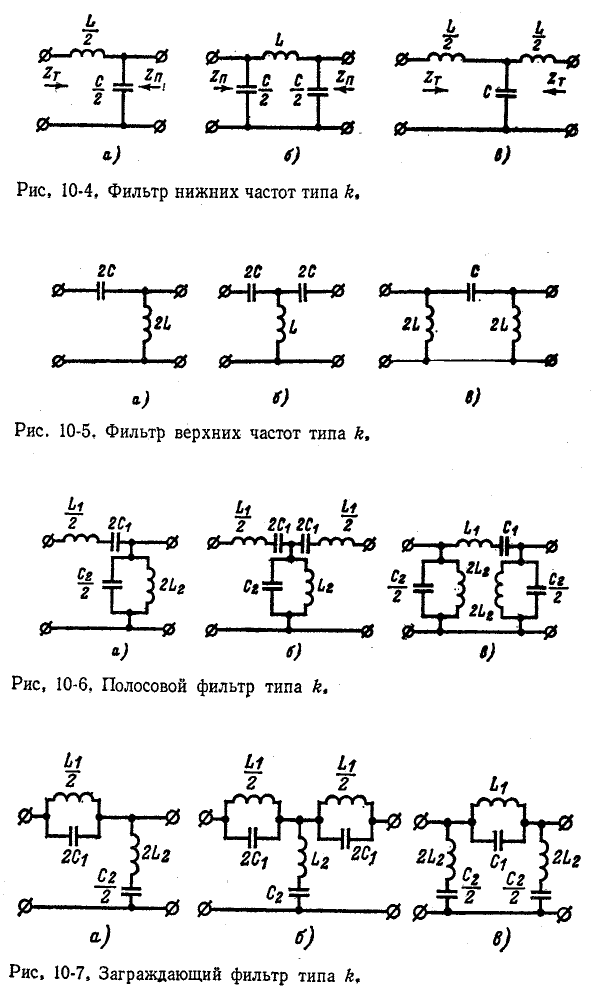
место обратное явление — индуктивные сопротивления велики, а емкостные малы. Поэтому например, в фильтре, нижних частот (см. рис. 10-4) токи нижних частот проходят через индуктивность в нагрузку, лишь в малой степени ответвляясь в емкость.

В области же верхних частот индуктивность представляет большое сопротивление и, кроме того, ток высокой частоты, прошедший через индуктивность, замыкается в основном через емкость, представляющую для него малое сопротивление.

Аналогичные рассуждения применимы и к фильтрам верхних частот (см. рис. 10-5), которые благодаря емкостному характеру сопротивления продольной ветви и индуктивному характеру сопротивления поперечной ветви обусловливают большое затухание на нижних частотах и малое затухание на верхних.

В свою очередь в полосовых и заграждающих фильтрах (рис. 10-6 и 10-7) проявляются частотные зависимости сопротивлений двухполюсников, состоящих из последовательно и параллельно соединенных индуктивностей и емкостей.

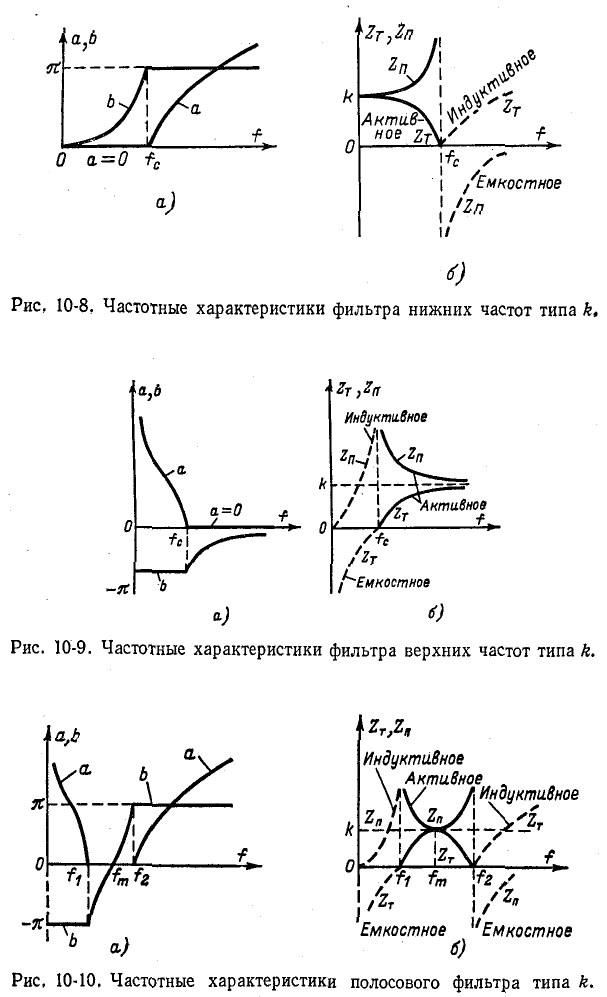
Частотные характеристики a, b, Zt и Zn рассматриваемых фильтров типа k изображены на рис. 10-8—10-11, а расчетные выражения основных характеристик и параметров фильтров сведены в табл. 10-1 * и 10-2. .

Как видно из расчетных выражений и характеристик (рис. 10-8 и 10-9), в пределах полосы пропускания напряжение на входе симметричного фильтра, нагруженного согласованно, опережает напряжение на выходе (b> 0 — фильтр нижних частот) или отстает от него (b < 0 — фильтр верхних частот); 'в случае полосового фильтра (рис. 10-10) знак b изменяется в пределах полосы пропускания с минуса на плюс. В полосе задерживания симметричного фильтра коэффициент фазы b равен b (фильтр нижних частот) или — 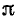(фильтр верхних частот); в случае симметричного полосового фильтра коэффициент фазы ниже полосы пропускания равен —- 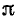, а выше полосы пропускания — равен .
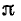1    [т

‘Примечание к табл, 10-1.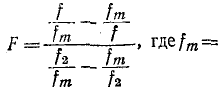

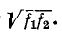
Выше отмечалось что коэффициент фазы Г-образного фильтра равен 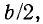и поэтому в полосе задерживания он равен 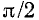или —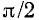 в зависимости от типа фильтра.

Если Г-образный фильтр нагружен согласованно, то угол фазового сдвига между напряжениями на входе и

выходе составляет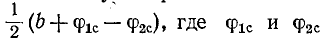 — углы

характеристических сопротивлений рассматриваемого Г-образного фильтра.

В полосе задерживания характеристические сопротивления мнимые, разного знака и соответственно разность

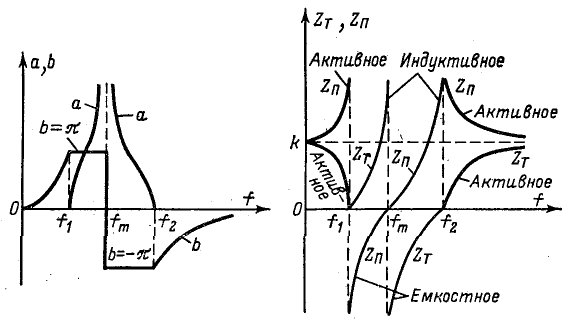
Рис. 10-11. Частотные характеристики заграждающего фильтра типа k.
углов 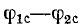составляет 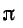или —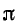. В этом случае угол между входным и выходным напряжениями Г-образного фильтра, нагруженного согласованно, с учетом того, Что в полосе затухания 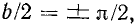получается равным ± 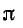. Это соответствует физическим представлениям о фазовых сдвигах в реактивных цепях, поскольку в полосе задерживания нагрузка.фильтра предполагается также реактивной.

Следует заметить, что если, например, Г-образный фильтр нижних частот согласованно нагружен со стороны выхода, имеющего характеристическое сопротивление 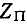, то в полосе пропускания нагрузка фильтра, равная 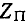, активна.

Можно показать, что в результате параллельного соединения активного сопротивления нагрузки (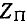) с емкостным сопротивлением поперечной ветви Г-образного звена 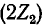получится активно-емкостное сопротивление, емкостная составляющая которого компенсирует индуктивное сопротивление продольной ветви (ZJ2). В результате останется только активная составляющая, равная характеристическому сопротивлению 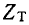при данной частоте f.

Для определения знака характеристического сопротивления фильтра в полосе задерживания (+ j или — j) удобно, пользоваться формулами табл. 10-1, в которых под корнем сохранен множитель j. В полосе задерживания слагаемое, содержащее множитель j, больше единицы; поэтому при отбрасывании слагаемого 1 под корнем остается выражение с множителем j в числителе или- знаменателе в зависимости от типа фильтра и от того, рассматривается л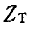и или .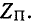

Преимуществом фильтров типа к является их простота, а также то, что в полосе задерживания затухания по мере удаления частоты от частоты среза неуклонно возрастает.

Что касается недостатков фильтров типа к, то они в основном заключаются в следующем:

1. Характеристические сопротивления 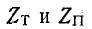в полосе пропускания фильтра очень резко изменяются в зависимости от частоты, вследствие чего согласовать нагрузку с фильтром удается только в ограниченной части полосы пропускания.
2. Кривая затухания вблизи частоты среза имеет недостаточную крутизну, вследствие чего не обеспечивается четкое разделение частот.

Для увеличения крутизны кривой затухания приходится применять многозвенный фильтр.

Фильтры типа m

В целях наилучшего согласования нагрузки с фильтром необходимо, чтобы характеристическое сопротивление фильтра было по возможности постоянным в полосе пропускаемых частот. В связи с этим попытаемся изменить продольную или поперечную ветвь Г-образного эвена типа k таким образом, чтобы получилось новое Г-образное звено с характеристическим сопротивлением, мало меняющимся в зависимости от частоты в полосе пропускания. Второе характеристическое сопротивление этого звена должно быть равно характеристическому сопротивлению исходного звена типа k (именуемого «прототипом»).

Равенство характеристических сопротивлений нового фильтра (так называемого фильтра типа m) и прототипа позволяет включать их согласованно и образовывать, таким, образом, комбинированные фильтры, сочетающие в себе преимущества фильтров обоих типов. Ввиду того что Г-об-разный прототип имеет два характеристических сопротивления, в данном случае возможны два варианта:

1. Одинаковыми остаются характеристические сопротивления 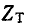(рис. 10-12). Полученное при этом звено m носит название последовательно-производного.
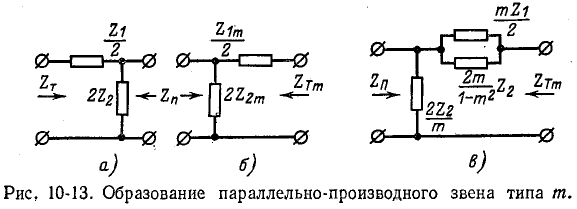
2. Одинаковыми остаются характеристические сопротивления 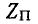(рис. 10-13). В этом случае звено m носит название параллельно-производного.

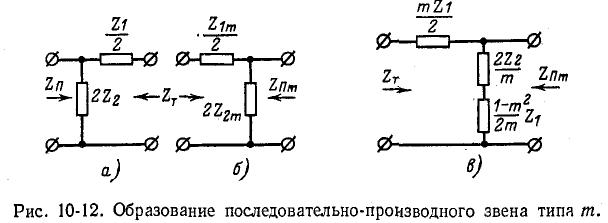
Рассмотрим первый вариант. Из условия равенства характеристических сопротивлений Zt звеньев, изображенных на рис. 10-12, а и б, следует: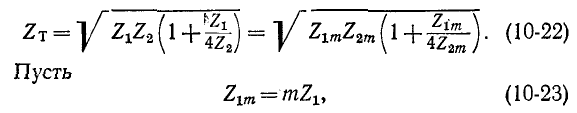

причем
Подстановка (10-23) в (10-22) и решение полученного уравнения относительно 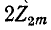дают:

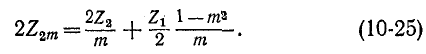
Из этого выражения видно, что поперечное плечо последовательно-производного Г-образного звена типа m состоит из двух последовательно включенных сопротивлений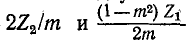 (см. рис. 10-12, в).

Рассмотрим теперь второй вариант. Исходя из условия равенства характеристических сопротивлений применительно к рис. 10-13, а и б, имеем:

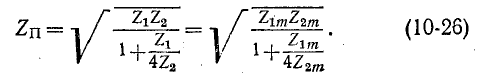
пусть
причем сохраняется условие (10-24).

После подстановки (10-27) в (10-26) решение уравнения относительно 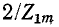дает:

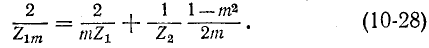
Значит, продольное плечо параллельно-производного Г-образного звена типа m состоит из сопротивлени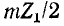й и 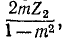   соединенных параллельно (рис. 10-13, в).

В соответствии с (10-25) и (10-28) могут быть найдены выражения характеристических сопротивлений 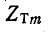(рис. 10-13) и 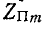(см. рис. 10-12):

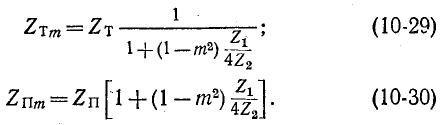
Очевидным является соотношение

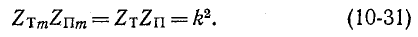
Полосы пропускания фильтров типа k и полученных из них фильтров типа m совпадают. Действительно, на основании (10-23) и (10-25) можно получить:

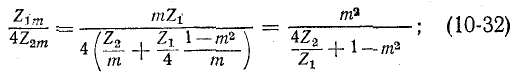
то же самое выражение получается на основании (10-27) и (10-28) для другого варианта фильтра типа m. Подставляя в (10-32) условия (10-13), отвечающие предельным частотам фильтра типа k, получаем при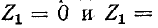

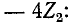
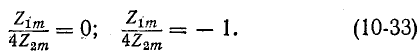
Эти условия соответствуют предельным частотам фильтра типа m (имеющего последовательно- или параллельно производное звено).

Следовательно, частоты среза для обоих типов фильтров совпадают.

О совпадении полос пропускания прототипа и производных от него звеньев можно также судить на основании равенства характеристических сопротивлений (в полосе пропускания характеристические сопротивления имеют действительные значения).

В полосе задерживания в соответствии с общей формулой (10-11)

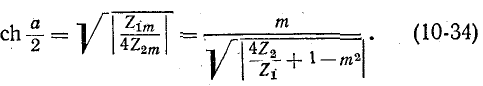
Затухание обращается в бесконечность при частоте 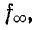при которой 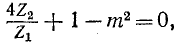или, что то же

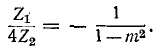
При этом условии 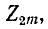выражаемое формулой (10-25), обращается в нуль. Это означает, что при 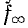наступает резонанс напряжений в поперечной ветви (в случае последовательно-производного звена). При этом же условии 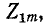выражаемое формулой (10-28), обращается в бесконечность, что означает резонанс токов в продольной ветви (в случае параллельно-производного звена.) Частота 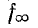называется частотой бесконечно большого затухания.

При переходе частоты через значение 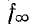, т. е. в области частот 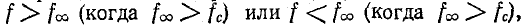сопротивления обоих плеч фильтра 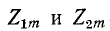имеют одинаковый знак. В этом случае в соответствиив левой части формулы (10-34) гиперболический косинус должен быть заменен гиперболическим синусом.

При 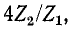стремящемся к нулю,

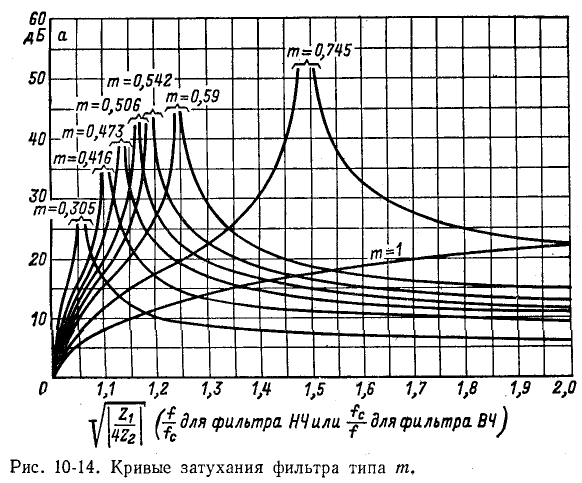
На рис. 10-14 показано семейство кривых собственного затухания а фильтра типа m (при разных значениях m) в функции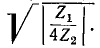

При m — 1 кривая затухания обращается в характеристику фильтра типа k.

Чем меньше коэффициент ь, тем меньше значение 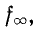т. е. тем круче кривая затухания а. Однако, как видно из рис. 10-14, предельное значение а при 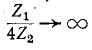уменьшается по мере снижения ь.

Наряду с большой крутизной кривой затухания фильтры типа ь отличаются от фильтров типа k относительно большим постоянством характеристических сопротивлений

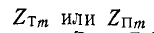(по сравнению с частотными характеристиками ).

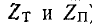На рис. 10-15 изображены кривые 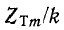и соответственно 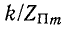в зависимости от величины 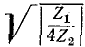равной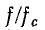

для фильтров нижних частот и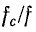 для фильтров верхних частот.

В спектре частот, соответствующем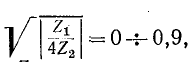

характеристические сопротивления 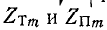отклоняются от k на ± 5% при m = 0,59 и на ± 10% при m = 0,54.

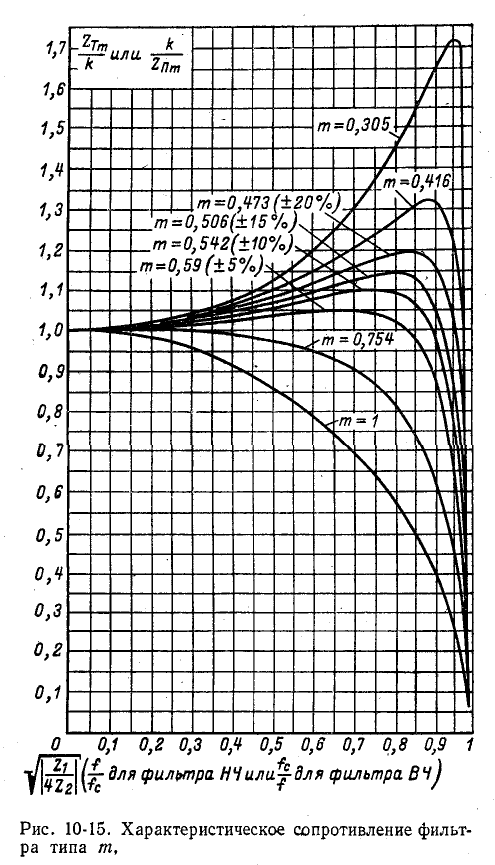
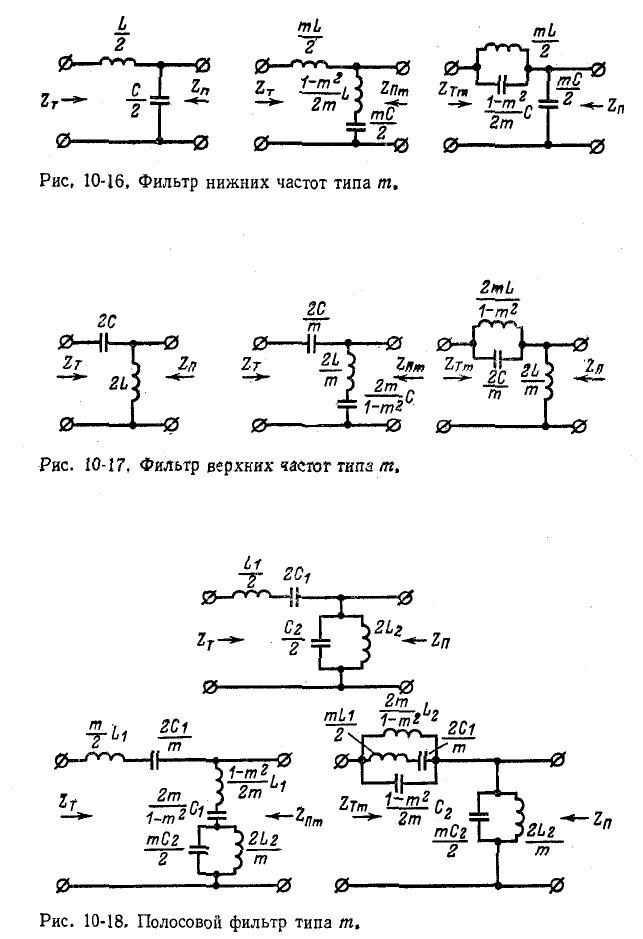
Типовые схемы Г-образных звеньев фильтров нижних частот, верхних частот и полосовых фильтров типов k и m

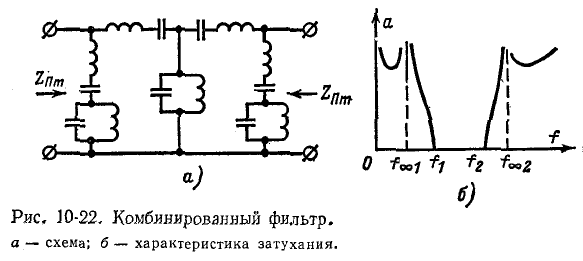
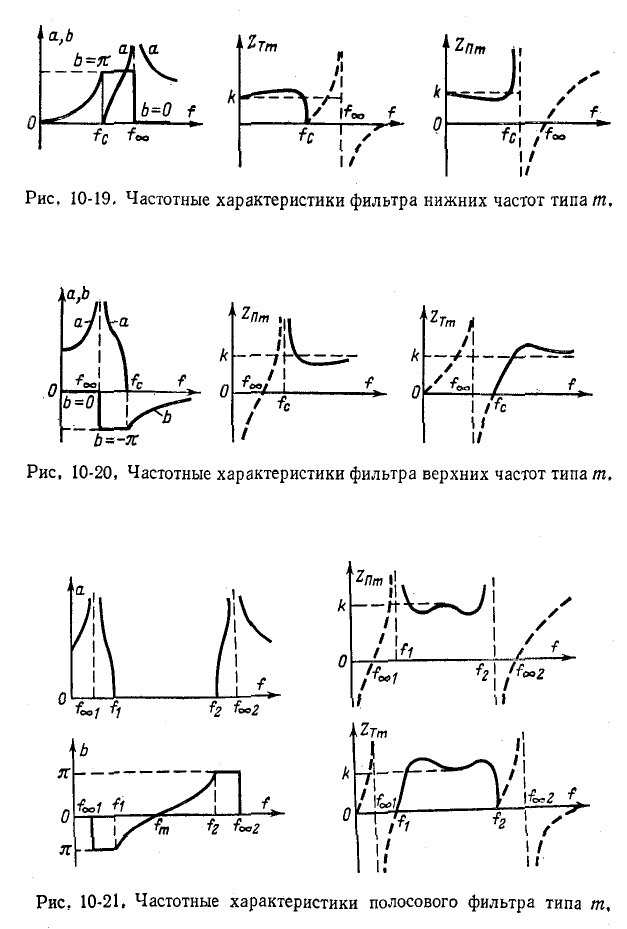
приведены на рис. 10-16—10-18; частотные характеристики фильтров тина m показаны на рис. 10-19—10-21.

Как видно из частотных характеристик, фильтры типа m имеют более постоянное характеристическое сопротивление в полосе пропускания, чем фильтры типа k. Кроме того, они обладают большей крутизной кривой затухания.

Недостатком фильтров типа m является снижение затухания при 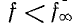(фильтры верхних частот и полосовые) и 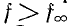(фильтры нижних частот и Полосовые).

Соединяя последовательно звенья типов k и m, можно достигнуть некоторого постоянства характеристических сопротивлений и крутизны кривой затухания при одновременном сохранении необходимого затухания ниже или выше частоты бесконечно большого затухания. На рис. 10-22, а в виде примера показан полосовой фильтр, состоящий из Т-образного фильтра типа k (в середине) и двух Г-образных звеньев типа m (по концам). На рис. 10-22, б изображена характеристика затухания такого фильтра.

Индуктивно связанные контуры как фильтрующая система

Индуктивно связанные контуры при соответствующем подборе параметров представляют собой полосовой фильтр, пропускающий заданную полосу частот.

Положим, что в первичную и вторичную цепи трансформатора включены емкости С (рис. 10-23, а).

Индуктивности обмоток трансформатора примем равными L; коэффициент индуктивной связи обозначим через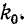

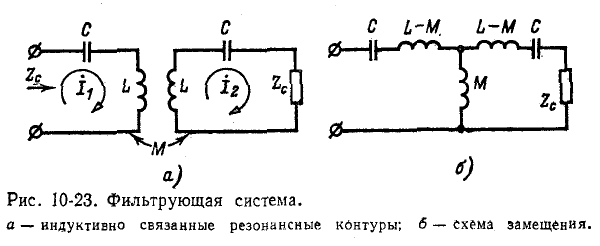
Трансформатор с емкостями С представляет собой симметричный четырехполюсник, эквивалентная схема которого показана на рис. 10-23, б. Выше мы уже встречались с аналогичной схемой полосового фильтра (см. рис. 10-2). Исследуем теперь более подробно фильтрующие свойства рассматриваемого четырехполюсника в предположении, что он нагружен согласованно. Его характеристическое сопротивление может быть вычислено по формуле (10-14), куда следует подставить:

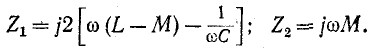
После преобразования получим:

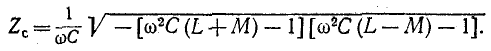
Приняв 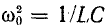и введя коэффициент индуктивной связи 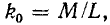получим окончательно:

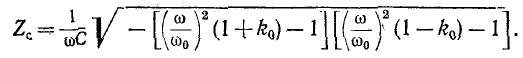
Характеристическое сопротивление 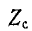действительно при условии, что выражения в квадратных скобках имеют разные знаки, а именно:

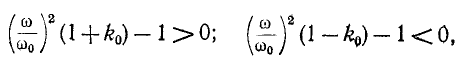
откуда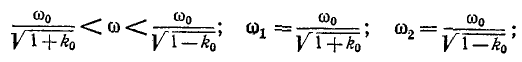

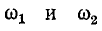представляют собой частоты среза данного полосового фильтра.

В области частот ниже ©! характеристическое сопротивление фильтра емкостное и с уменьшением частоты приближается к —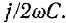

В области частот выше 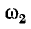характеристическое со-

противление фильтра индуктивное и с увеличением частоты приближается к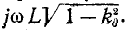

При частоте

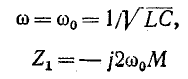
и

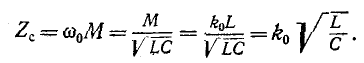
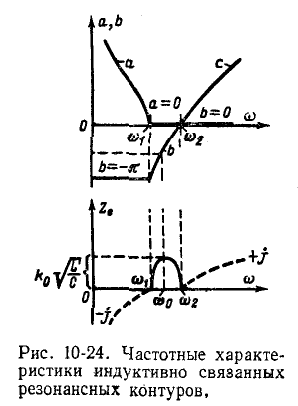
На рис. 10-24 показаны частотные характеристики данного фильтра.

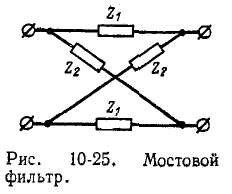
Мостовые фильтры. Пьезоэлектрические резонаторы

Согласно [формулы (9-50)] характеристическое сопротивление и мера передачи симметричного мостового фильтра (рис. 1025) находятся по формулам:

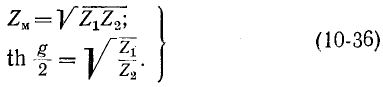
Полоса пропускания фильтра (а = 0) имеет место при мнимых значениях корня 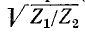и действительных значениях корня 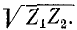При этом 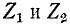имеют разные знаки.

Коэффициент фазы определяется в этом случае по формуле

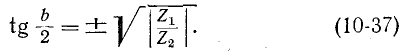
В полосе задерживания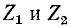 имеют одинаковые знаки. В этой полосе, возможны два случая:

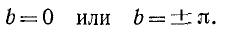
В первом случае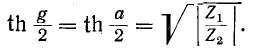
Это решение соответствует условию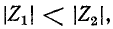так как гиперболический тангенс не может превышать единицу. Во втором случае

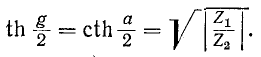
Данное решение соответствует условию 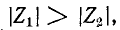так как гиперболический котангенс не может быть меньше единицы.
При 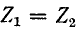затухание 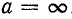, так как при этом  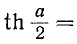1 и напряжение на выходе мостовой схемы равно нулю. Физически это объясняется тем, что мост уравновешен.

На рис. 10-26 показаны простейшие схемы мостовых фильтров: нижних частот, верхних частот, полосового и заграждающего.

Основываясь на том, что в полосе пропускания 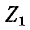и 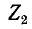имеют разные знаки, а в точке пересечения кривых 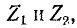, т. e. при 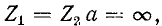можно легко найти частоты среза и бесконечно большого затухания. В виде примера

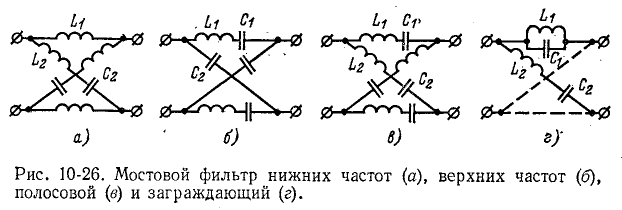
это показано применительно к фильтру нижних частот на рис. 10-27. При отсутствии пересечения кривых 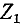и 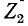частота бесконечно большого затухания отсутствует или удалена в бесконечность (при асимптотическом приближении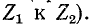

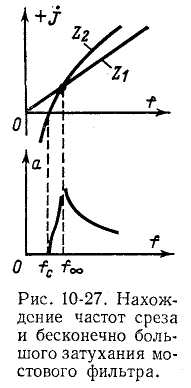
На практике применяются также мостовые схемы с дифференциальным трансформатором (дифференциально-мостовые схемы), эквивалентные по своим электрическим качествам мостовым схемам, но имеющие меньшее число элементов (рис. 10-28).

Следует заметить, что в соответствии с (10-36) 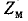зависит от произведения, a g — от отношения сопротивлений плеч мостового фильтра. Поэтому характеристические параметры 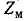и g мостового фильтра не связаны друг с другом в той мере, как это, например, имеет место в Т- и П-образных фильтрах (см. задачу 10-16) и, следовательно, 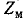и g могут выбираться независимо друг от друга. Это свойство является одним из преимуществ мостовых фильтров по сравнению с другими.

Мостовые фильтры часто выполняются с помощью пьезоэлектрических резонаторов. Последние представляют собой электромеханическую систему, состоящую из пьезоэлектрической пластинки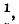 электродов и держателя. Пьезоэлектрическая пластинка под воздействием переменного электрического поля совершает механические колебания с частотой приложенного напряжения. При этом на ее поверхностях возникают электрические заряды. При совпадении частоты поля с частотой собственных колебаний пластинки наступает резонанс: амплитуда колебаний и соответственно заряд на пластинке достигают максимума.

¹ В технике связи применяются преимущественно кварцевые пластинки

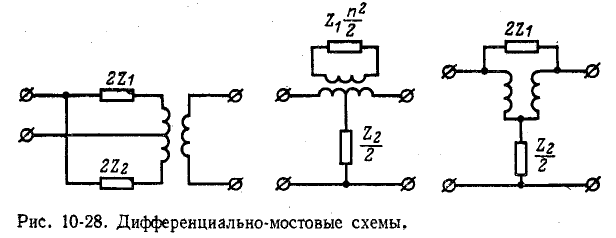
Эквивалентная электрическая схема пьезоэлектрического резонатора представляет собой двухполюсник (рис. 10-29, а). Частотная характеристика реактивного сопротивления резонатора изображена на рис. 10-29, б,

В отличие от индуктивных катушек, добротность которых в лучшем случае измеряется сотнями единиц, добротность пьезоэлектрических резонаторов достигает десятков тысяч.

С помощью таких резонаторов удается получить полосовые фильтры с весьма узкой полосой пропускания и высокой крутизной кривой за-

тухания вблизи частот среза (кварцевые мостовые фильтры допускают полосу пропускания порядка 20—50 Гц при частоте 500 кГц).

Емкость 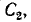входящая в систему замещения пьезоэлектрического резонатора (рис. 10-29, а), значительно превышает емкость С; поэтому частоты 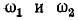(рис, ГО-29, б) располагаются весьма близко друг к другу.

Безындуктивные фильтры

Изготовление индуктивных катушек для фильтров, работающих в области низких частот, сопряжено с трудностями, особенно когда катушки должны иметь большую индуктивность при высоком коэффициенте добротности. Увеличение сечения обмотки повышает массу, размеры и стоимость катушки, применение же магнитопровода создает зависимость индуктивности от тока, проходящего по обмотке.

Применение пьезокварцевых резонаторов для фильтров низких частот также не всегда возможно, так как самая низкая частота, на которую изготовляется кварц, составляет несколько сотен герц.

Во избежание получения громоздких фильтров с низкой добротностью катушек применяют безындуктивные фильтры (гС-фильтры), состоящие из активных сопротивлений и емкостей.

На рис. 10-30 показан rC-фильтр нижних частот. При низких частотах, когда емкостное сопротивление велико, напряжение на выходе фильтра немногим меньше напряжения на его входе и, следовательно, затухание мало. С повышением частоты емкостное сопротивление убывает, напряжение на выходе уменьшается и, следовательно, затухание возрастает.

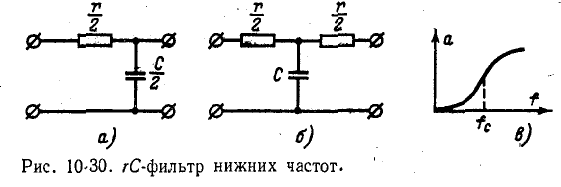
На рис. 10-30, в показана частотная характеристика собственного затухания такого фильтра. Ввиду малой крутизны кривой затухания однозвенного rC-фильтра применяют двух- или трехзвенный фильтр, однако при этом увеличивается затухание и в полосе пропускания.

На основании (10-1)

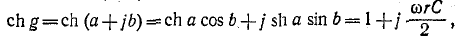
откуда

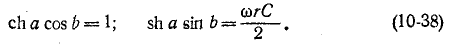
При постоянном токе

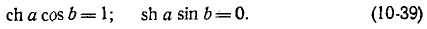
Эти равенства удовлетворяются при а = 0 и b = 0 одновременно.

При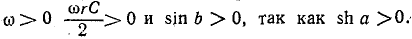

Итак, в отличие от реактивных фильтров, рассмотренных в предыдущих параграфах, гС-филътр не имеет области частот, в пределах которой собственное затухание а равно нулю.

Частотные характеристики гС-фильтр а нижних частот могут быть построены по выражениям для а и b, которые получаются в результате совместного решения уравнений (10-38), первое из которых можно представить в следующем виде:

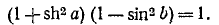
Подставляя сюда выражение для sin b, получаемое из второго уравнения (10-38), приходим к биквадратному уравнению

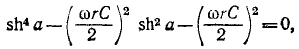
откуда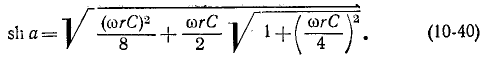

При значениях 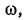при которых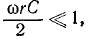

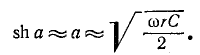
За частоту среза rС-фильтра нижних частот условно принимается частота, при которой равны активное и емкостное сопротивления ветвей Г-образного звена, т. е.

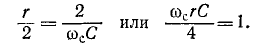
В этом случае выражение (10-40) дает sh а = 2,2, откуда а = 13,3 дБ.

На рис. 10-31 представлен rС-фильтр верхних частот с примерной частотной характеристикой затухания.

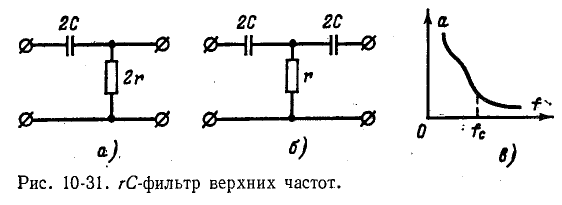
При низких частотах, когда емкостное сопротивление велико, напряжение на выходе фильтра мало, т. е. получается большое затухание (при постоянном токе — бесконечно большое). С увеличением частоты емкостное сопротивление уменьшается и напряжение на выходе возрастает, т. е. затухание убывает. Частотная характеристика собственного затухания такого фильтра показана на рис. 10-31, в.

Для повышения крутизны кривой затухания применяются несколько звеньев, однако при этом неизбежно увеличивается затухание и в полосе пропускания.

Пользуясь формулой (10-1), получаем в рассматриваемом случае: 

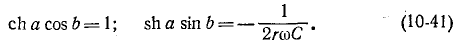
При бесконечно большой частоте 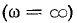получаются условия (10-39), которые, как было установлено выше, выполняются, если одновременно а и b равны нулю.

При значениях 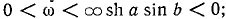поскольку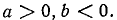

Совместное решение уравнений (10-41) приводит к биквадратному . уравнению

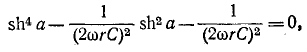
откуда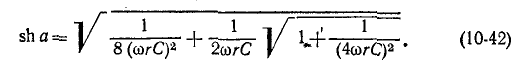

При значениях 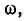при которых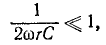

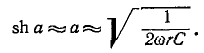
Если за частоту среза условно принять частоту, при которой сопротивления ветвей Г-образного звена равны друг другу,

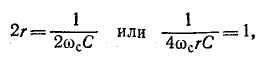
то на оснований (10-42) будем иметь: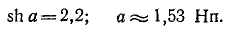

Простейшие схемы полосового и заграждающего rС-фильтров и примерные частотные характеристики затухания приведены на рис. 10-32 и 10-33.

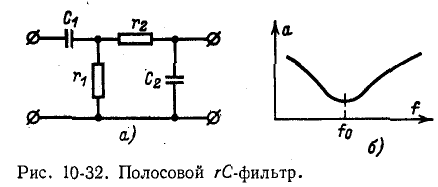
Полосе вой rC-фильтр основан на том, что емкость первого звена обусловливает затухание более низких частот, а емкость второго звена— затухание более высоких частот. Средняя частота полосы пропускания, при которой собственное затухание фильтра минимально (рис. 10-32, б), ориентировочно равна:

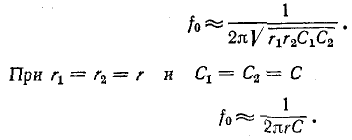
Как видно из рис. 10-33, а, заграждающий rC-фильтр состоит из двух параллельно соединенных Т-образных rС-фнльтров верхних и нижних частот. Соответствующим подбором параметров элементов можно добиться того, что при определенной частоте токи на выходе обеих Т-образных схем будут равны и противоположны по знаку, вследствие чего ток в нагрузке будет равен нулю. Следовательно, затухание на этой частоте будет бесконечно большим (рис. 10-33, б).

rC-фильтры часто применяются в сочетании с усилителем. В этом случае в полосе пропускания не только отсутствует затухание, но, наоборот, имеет место усиление.

Топологические формулы нахождения определителей и алгебраических дополнений

При анализе линейных электрических цепей используют два основных топологических метода — метод деревьев (или топологических формул) и метод сигнальных графов.

Расчет электрических цепей по методу узловых напряжений требует согласно формуле (7-6) вычисления определителя системы и его алгебраических дополнений. Эта задача может быть облегчена, если применить метод деревьев.

Определитель системы по методу узловых напряжений для цепи на рис. 7-8:

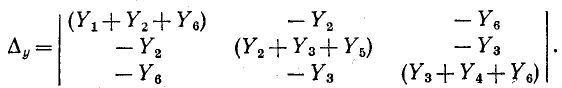
Раскрыв определитель, получаем выражение, содержащее алгебраическую сумму 38 произведений проводимостей ветвей. После приведения подобных членов в выражении останется только 16 членов. 22 члена взаимно уничтожаются и получаем:

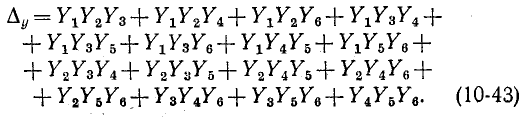
Выражение (10-43) можно получить без записи лишних взаимно уничтожающихся членов, основываясь на том, что каждый член уравнения содержит произведение проводимостей ветвей, принадлежащих некоторому дереву графа цепи.

Произведение проводимостей ветвей дерева называется величиной (весом) дерева.

Для любого дерева, которое можно выбрать в графе цепи, в выражении (10-43) имеется соответствующий член. Отсюда следует правило: определитель системы уравнений по методу узловых напряжений равен сумме величин всех деревьев графа цепи.

Поскольку в соответствии с приведенным правилом определитель системы уравнений вычисляется по графу цепи, то-его называют также определителем графа цепи.

Обозначим величину k-ro дерева через 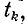тогда выражение для определителя можно записать так:

где k — все деревья.

Суммирование в формуле (10-44) распространяется на все деревья графа цепи.

Чтобы не пропустить ни одно дерево, располагаем ветви, принадлежащие дереву, в порядке возрастания их номеров, а сами деревья записываем в порядке возрастания номеров как первых, так и последующих ветвей. Именно по такому принципу записаны величины деревьев в выражении (10-43).

Для нахождения алгебраических дополнений используются понятия 2-дерева и величины (веса) 2-дерева.

2-деревом графа цепи называется такая часть графа (подграф), которая содержит все узлы графа, не содержит ни одного контура и состоит из двух изолированных частей. 2-дерево содержит q — 2 ветви, так как при добавлении к нему одной ветви, соединяющей изолированные части, оно превращается в дерево.

Примером 2-дерева графа цепи на рис. 7-8 может служить подграф из ветвей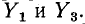Ветви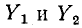тоже образуют 2-дерево. Одна часть этого 2-дерева содержит ветв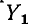и и 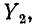а также узлы 1, 2 и 4. Вторая часть состоит только из узла 3.

Произведение проводимостей ветвей 2-дерева называется величиной (весом) 2-дерева.

Рассмотрим алгебраическое дополнение 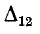определителя 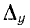у цепи на рис. 7-8:

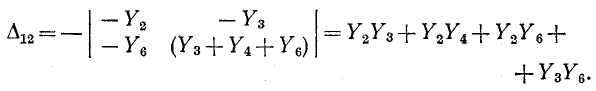
Последнее выражение содержит сумму величин 2-деревьев. В этой сумме учтены не все 2-деревья, а только такие, которые содержат узлы 1 и 2 в одной части 2-дерева, а базисную вершину 4 — в другой.

В результате получаем правило: алгебраическое дополнение 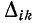определителя 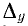равно сумме величин таких 2-деревьев, у которых узлы i и k находятся в одной части 2-дерсва, а базисная вершина q — в другой.

Обозначим величину упомянутого выше 2-дерева через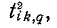 тогда можно записать:

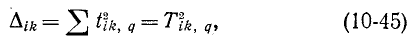
где суммирование распространяется на все 2-деревья, у которых вершины, разделенные запятой в обозначении 2-дерева, находятся в разных его частях.
 

Топологические формулы разложения

Приведенные выше топологические формулы имеют тот недостаток, что приходится в сложных графах находить

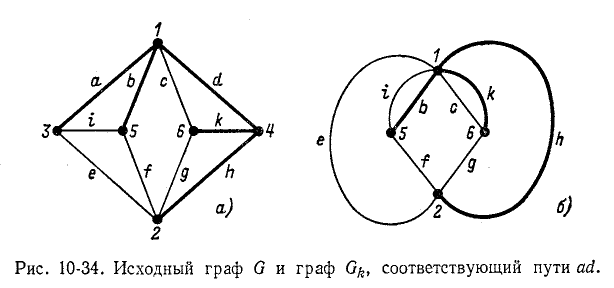
большое число деревьев. Так, в графе на рис. 7-8 число деревьев равно 16, а в графе на рис. 10-34—128.

С ростом числа ветвей число деревьев быстро увеличивается. Для облегчения задачи нахождения суммы величин деревьев и для более компактной записи этой суммы используются формулы разложения.

Формула разложения по путям

Путем в графе называется такая последовательность ветвей, в которой начало последующей ветви совпадает с концом предыдущей. Величиной (весом) пути называется произведение проводимостей ветвей пути. Путь, а также его величину обозначим буквой Р.

Определитель графа цепи, получающейся после закорачивания всех ветвей пути 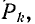называется алгебраическим дополнением пути 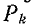и обозначается через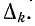

Формула разложения определителя по путям записывается следующим образом:

где суммирование распространяется на все пути в графе цепи между двумя выбранными узлами.

Таким образом, определитель системы уравнений по методу узловых напряжений равен сумме произведений величин путей между двумя выбранными узлами на соответствующие им алгебраические дополнения.

Докажем последнее утверждение, для чего рассмотрим граф некоторой цепи, который обозначим буквой G. Для любых выбранных узлов существует путь по ветвям дерева графа G, соединяющий эти вершины. Закоротим в графе G ветви пути 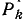между выбранными узлами, тогда получим новый граф 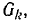в котором оставшиеся незахороненными ветви дерева графа G образуют дерево трафа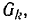

Например, если в дереве, которое показано толстыми линиями на рис. 10-34, а, закоротить ветви and пути между узлами 3 и 4, то получим граф 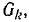показанный на рис. 10-34, б. В этом графе ветви b, k и h образуют дерево.

С другой стороны, если в графе 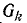выбрать любое другое дерево, то оно вместе с ветвями пути 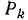образует дерево графа G.

Таким образом, для каждого дерева графа G, содержащего путь 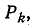существует единственное дерево графа 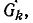и наоборот.

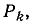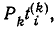Величина ш-ro дерева, содержащего путь равна где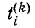
— величина i-го дерева графа 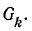Сумма величин всех деревьев, содержащих путь 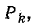равна:

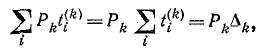
так как сумма величин всех деревьев типа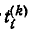 равна определителю цепи, соответствующей графу 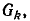т. е.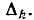

Определитель 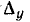равен сумме всех деревьев для всех возможных путей грйфа G, т. е. члены вида 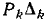нужно просуммировать для всех путей, что приводит к формуле (10-46).

Вычисляя алгебраическое дополнение 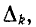можно также использовать формулу разложения по путям.

Пример 10-1.

Найти определитель цепи на рис. 7-8 разложением по путям между узлами 2 и 4.

Между узлами 2 и 4 можно проследить следующие пять путей:

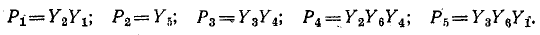
После закорачивания ветвей первого пути 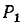получаем граф, состоящий из трех параллельных ветвей с проводимостями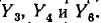

Определитель такого графа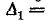 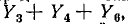так как любая из трех ветвей является деревом.

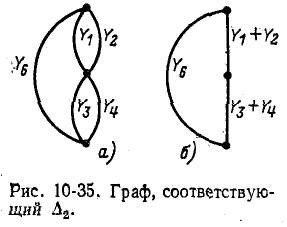
Если закоротить ветви пути 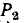(т. е. ветвь с проводимостью 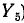), получим граф, показанный на рис. 10-35, а. После замены параллельных ветвей эквивалентными преобразуем его к графу на рис. 10-35, б, определитель которого

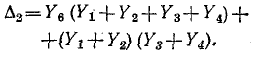
Для пути 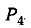алгебраическое дополнение 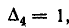так как при закорачивании ветвей пути 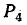все ветви оказываются закороченными. Аналогичным образом находим алгебраические дополнения

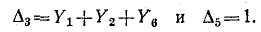
Подставляя найденные величины путей и алгебраических дополнений в формулу (10-46), получаем:

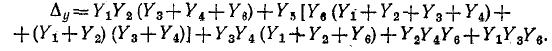
Разложение определителя по узлу

Пусть к некоторому узлу s подходят ветви с проводимостями 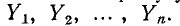Поскольку все деревья касаются узла s, то любое дерево содержит хотя бы одну ветвь, касающуюся узла s. Среди этих деревьев имеются содержащие одну, две, три и т. д. ветвей, подходящих к узлу s.

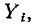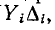Сумма величин деревьев, содержащих ветвь с проводимостью равна где 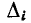— определитель графа, получающегося при закорачивании ветви с проводимостью К* и удалении остальных ветвей, подходящих к узлу s.

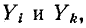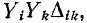Аналогично сумма величин деревьев, содержащих ветви с проводимостями равна , где 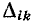— определитель графа, получающегося при закорачивании ветвей с проводимостями 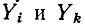и удалении остальных ветвей, подходящих к узлу s.

Суммируя величины деревьев всех типов, получаем: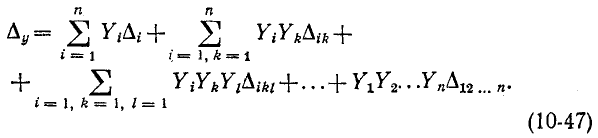

Под знаком суммы в формуле (10-47) стоят произведения разных проводимостей 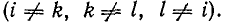Легко убедиться, что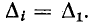

Пример 10-2.

Найти определитель цепи на рис. 7-8, используя формулу разложения по узлу 1.

Для данного примера формулу (10-47) запишем в виде

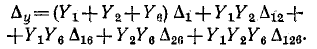
Определитель 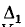соответствует графу на рис.

10-36 и равен 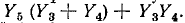После закорачивания ветвей 1 и 2 и удаления ветви 6 останутся параллельно соединенные ветви 3 и 4, т. е.  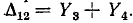Аналогично 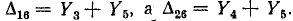После закорачивания ветвей 1, 2 и 6 все ветви будут закорочены, т. е.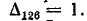

С учетом приведенных выше значении находим:

 

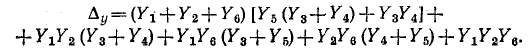
Разложение алгебраических дополнений по путям

В соответствии с формулой (10-45) алгебраическое дополнение 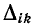равно сумме величин всех 2-деревьев типа 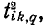у которых узлы i и k находятся в одной части 2-дерева, а базисный узел q — в другой. На рис. 10-37 условно изображено одно из таких 2-деревьев.

Добавим к 2-дереву ветвь с проводимостью, равной единице, и соединяющую узлы k и q (показано пунктиром на рис. 10-37). В результате получаем дерево, величина которого равна величине исходного 2-дерева и которое содержит путь от узла i к узлу q через узел k и единичную ветвь.

Можно осуществить обратную операцию: добавить единичную ветвь к исходному графу цепи и выбрать в нем произвольное дерево, содержащее путь от узла i к узлу q через единичную ветвь. Если удалить из этого дерева единичную ветвь, то оно превращается в 2-дерево типа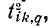 т. е. между деревьями и 2-деревьями указанного выше типа существует взаимно однозначное соответствие.

Из сказанного выше следует, что алгебраическое дополнение 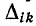равно сумме величин всех деревьев, содержащих путь от узла i к узлу k через единичную ветвь, т. е.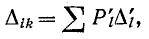

где 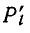— величина l-го пути от узла i к узлу q через единичную ветвь;

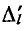— алгебраическое дополнение этого пути.

Пример 10-3.

Найти алгебраическое дополнение 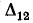графа цепи на рис. 7-8.

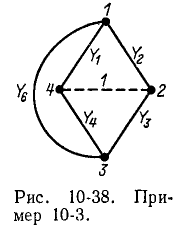
После добавления единичной ветви, соединяющей узлы 2 и 4 (базисный) поручим цепь, граф которой изображен на рис. 10-38. Ветвь 5 удалена из графа, так как она шунтируется любым путем, проходящим через единичную ветвь, и не может поэтому принадлежать алгебраическому дополнению пути.

Записываем пути между узлами 1 и 4, а также их алгебраические дополнения:

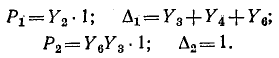
Следовательно,

 

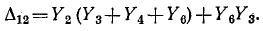
Топологические формулы для передаточных функций

Было отмечено, что передаточная функция определяется как отношение выходной величины четырехполюсника к входной, причем это отношение зависит от нагрузки. Ниже при рассмотрении передаточных функций в качестве выходной величины примем напряжение холостого хода или ток короткого замыкания. Это не нарушает общности, так как, если сопротивление нагрузки отлично от нуля или бесконечности, то его можно внести внутрь четырехполюсника.

К входу четырехполюсника подключим идеальный источник э. д. с., если входная величина — напряжение, или идеальный источник тока, если входная величина—ток. На выходе подключим вольтметр в случае холостого хода или амперметр при коротком замыкании. На рис. 10-39 условно показано подключение источника И и измерительного прибора П. Полярности источника и прибора соответствуют выбранным положительным направлениям напряжений.

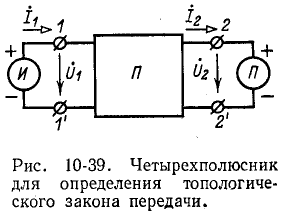
Передаточные функции любого типа для схемы на рис. 10-39 определяются с помощью топологического закона передачи, который выражается формулой

где К — передаточная функция;

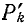— величина пути от плюса источника к его минусу, проходящего через измерительный прибор;

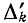— алгебраическое дополнение пути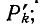

— определитель графа цепи, получающейся после закорачивания источника э. д. с. и амперметра, а также удаления источника тока и вольтметра.

При определении величины пути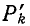 проводимость прибора считаем равной единице (единичная ветвь). Путь 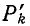берем с плюсом, если измерительный прибор проходим в положительном направлении, иначе 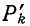берем с минусом. Определитель 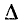можно находить разложением по путям между любыми вершинами.

Доказательство справедливости формулы (10-48) сделаем на примере передаточного сопротивления

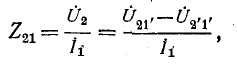
где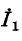— ток источника тока на входе цепи.

Подставив в последнее уравнение выражения узловых напряжений 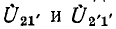согласно формуле (7-6), получим:

Алгебраическое дополнение 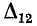согласно формуле (10-45) равно сумме величии 2-деревьев типа 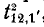у которых узлы 1 и 2 находятся в одной части 2-дерева, а базисный узел 1', — в другой. Что касается узла 2'. то он может быть или в той части, где находятся узлы 1 и 2, или в той, где узел 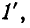т. е.

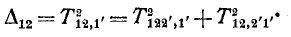
В этом уравнении, как и ранее, запятая разделяет номера узлов, принадлежащих разным частям 2-дерева.

По аналогии можно записать, что

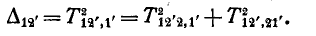
Подставляя полученные выражения для 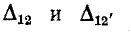в уравнение (10-49), находим:

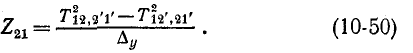
2-деревья типов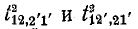 преобразуются в деревья добавлением единичной ветви, соединяющей узлы 2 и 2'.
Эти деревья содержат путь от плюса источника к его минусу через единичную ветвь (рис. 10-40). Причем для 2-дерева 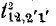единичная ветвь проходится в пути от узла 2 к узлу 2', а для 2-дерева 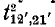' — в обратном направлении.

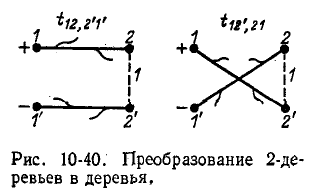
Соответственно в выражение (10-50) первое 2-дерево входит с плюсом, а второе — с минусом.

Разлагая суммы 2-деревьев 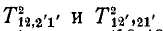по путям описанного выше типа, получаем формулу (10-48), в которой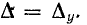

Аналогичным образом можно доказать справедливость формулы (10-48) для других типов передаточных функций.

Топологический закон передачи можно использовать также для определения входного сопротивления и проводимости, если считать, что вход и выход совпадают. В этом случае имеется единственный путь 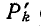от узла 1 к узлу 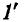непосредственно через измерительный прибор. Величина этого пути равна единице, а алгебраическое дополнение равно определителю цепи при закороченном входе.

Следовательно, входное сопротивление

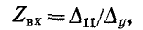
где 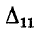— определитель цепи при закороченном входе;

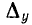— определитель цепи при разомкнутом входе.

Пример 10-4. Найти передаточную проводимость для цепи на рис. 10-41, а в режиме короткого замыкания и коэффициент передачи по напряжению в режиме холостого хода,

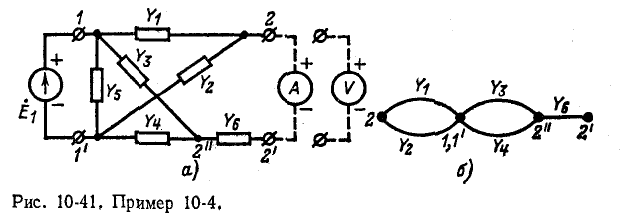
При определении передаточной проводимости на входе включаем источникэ. д. с.,анавыходе — амперметр. Используем формулу (10-48). В числителе этой формулы сумма произведений величин путей от узла 1 к 1' через амперметр на их алгебраические дополнения. В цепи существуют только два таких пути: .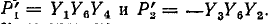

Алгебраические дополнения путей равны единице.

Следовательно,

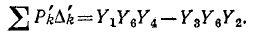
В знаменателе формулы (10-48) стоит определитель графа цепи, которая получается из исходной после закорачивания э. Д. с. и амперметра. Этот граф совпадает с графом на рис. 10-35, определитель которого

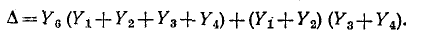
Подставляя найденные величины в (10-48), находим:

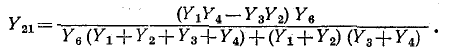
При определении коэффициента передачи по напряжению на входе цепи вместо амперметра следует включить вольтметр. Поскольку сама схема цепи и характер включения измерительного прибора не изменяются, то пути от узла 1 к узлу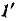 останутся теми же, Соответственно числитель формулы (10-48) не изменится.

Для вычисления определителя нужно закоротить вход и удалить вольтметр. Граф результирующий цепи показан на рис, 10-41, б. Определитель этого графа

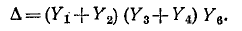
Окончательно получаем:

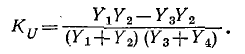
Проводимость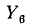 в числителе и знаменателе сокращается. Это можно было учесть с самого начала, подключив вольтметр к точке 2", так как напряжение на проводимости 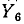равно нулю,

Топологический анализ активных цепей

Рассмотренный выше топологический анализ линейных цепей применим к пассивным обратимым цепям без взаимной индуктивности. Если имеется взаимная индуктивность, то от нее можно избавиться, используя развязку индуктивных связей. Необратимые цени могут быть заменены эквивалентными схемами замещения с зависимыми источниками энергии.

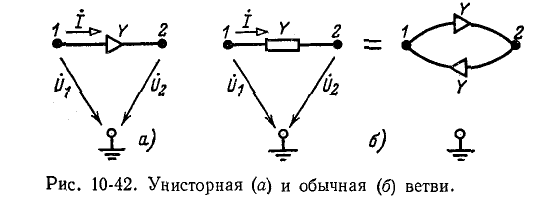
Для того чтобы можно было применить топологические методы для анализа электрических цепей с зависимыми источниками, вводится в рассмотрение элемент, называемый унистором (рис. 10-42, а).

Унистор — несимметричный элемент, пропускающий ток только в одном направлении, указанном стрелкой. Ток определяется равенством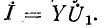

Для обычной ветви ток

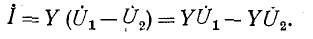
Следовательно, обычная ветвь эквивалентна параллельному соединению противоположно направленных унисторов с проводимостью, равной проводимости ветви (рис. 10-42, б),

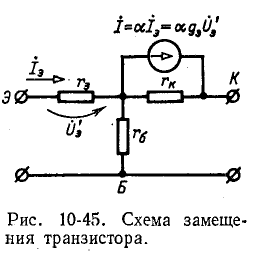
Зависимый источник тока, управляемый напряжением (рис. 10-43, а), можно заменить унисторной схемой замещения на рис. 10-43, б. Эквивалентность этих схем .четко проверить, вычисляя токи, входящие в узлы цепи.

Зависимые источники других типов целесообразно преобразовать в зависимый источник тока, управляемый напряжением, чтобы можно было использовать схему замещения на рис. 10-43, б.

 

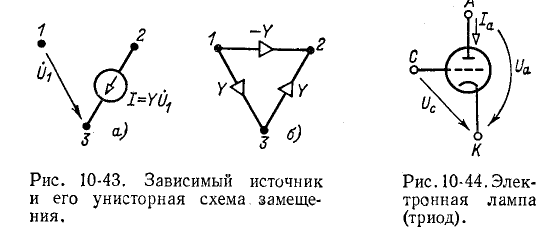
Схемы замещения с зависимыми источниками используются при анализе электронных схем в линейном режиме. Например, электронная лампа триод (рис. 10-44), используемая для усиления переменных сигналов, при пренебрежении внутренним сопротивлением эквивалентна зависимому источнику тока, показанному на рис. 10-43, а. При этом узел 1 соответствует сетке С, узел 2 — аноду А и узел 3 — катоду К. Роль проводимости Y в этом случае выполняет крутизна лампы S. Соответственно ток лампы

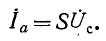
Чтобы учесть внутреннюю проводимость лампы 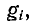ее включают параллельно источнику тока в схеме на рис. 10-43, а.

На рис. 10-45 показана схема замещения транзистора, которая содержит зависимый источник тока. Здесь 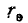— сопротивление эмиттера; 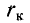— сопротивление коллектора; 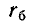— сопротивление базы. Если заменить —

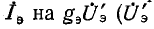напряжение на сопротивлении эмиттера), то получим источник тока, управляемый напряжением 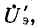который заменяется унисторной схемой на рис. 10-43, б с Y =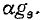

Основные топологические .правила, применимые к обычным цепям, справедливы и для цепей, содержащих унисторы. Все отличия сводятся к следующему:

1. в рассмотренных выше топологических формулах учитываются только такие деревья, 2-деревья или пути, в которых все унисторы направлены в сторону базисного (заземленного) узла;
2. в случае 2-дерева базисный узел выбирают в каждой части 2-дерева;
3. при использовании топологического закона передачи заземленным узлом должен быть один из выводов измерительного прибора.

Пример 10-5.

На рис. 10-46, а показана схема катодного повторителя. Определить для нее передаточную проводимость, представляющую собой отношение тока катода к входному напряжению,

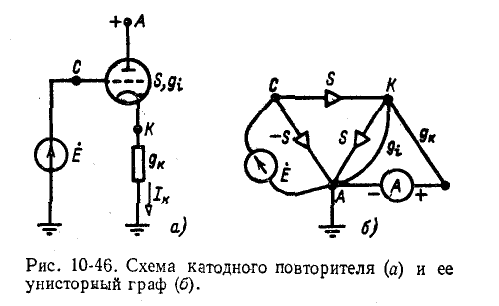
На анод схемы подано постоянное по отношению к земле напряжение. Поскольку, анализируя усиление сигналов, постоянную составляющую отбрасывают, можно считать, что анод присоединен к земле. С учетом этого после замены лампы унисторной схемой замещения получаем граф на рис. 10-46, б. В этой схеме существует лишь один путь 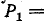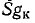— от плюса источника к минусу через амперметр. Этот путь следует учесть, так как унистор направлен к заземленному узлу. Алгебраическое дополнение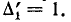

Для нахождения определителя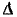 в знаменателе формулы (10-48) закорачиваем источник и амперметр. Получаем граф из проводимостей 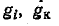и Двух унисторов, соединенных параллельно. Любая из этих

ветвей образует дерево. Однако один из унисторов следует отбросить, так как он направлен от заземленного узла. Следовательно,

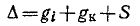
и передаточная проводимость

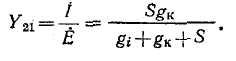
Сигнальные графы и методы их преобразования

Выше был рассмотрен топологический метод, использующий понятие деревьев. Особенность этого метода в том, что он оперирует с графом электрической схемы, отображающим ее топологию.

Сигнальные графы, применяемые для анализа электрических цепей, не отображают топологию электрических схем. Они используются для решения систем линейных уравнений и их конфигурация определяется этой системой.

Возьмем, например, систему уравнений, полученных для схемы рис. 7-6 в примере 7-2. Длд построения сигнального графа необходимо сначала разрешить каждое уравнение относительно одной переменной (разной для разных уравнений). Разрешим, например, первое уравнение относительно 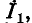второе — относительно 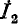и третье относительно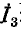

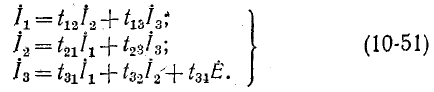
Здесь коэффициенты

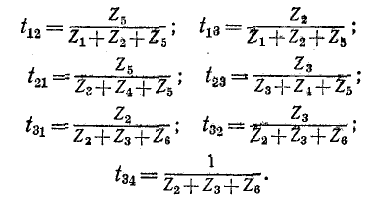
Полученной системе уравнений соответствует сигнальный граф, изображенный на рис. 10-47, а.

Сигнальный граф обладает следующими свойствами:

1. Сигнальный граф состоит из узлов и ветвей. Ветвь изображается направленным отрезком,
2. соединяющим два узла сигнального графа. Направление ветви указывается стрелкой.
3. Каждая ветвь графа характеризуется передачей ветви 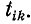Первый индекс ветви (i) соответствует номеру узла, в который входит ветвь, а второй (к) — номеру узла, из которого она выходит.
4. В каждом узле графа имеется сигнал, который передается от узла по всем ветвям, выходящим из него. При решении уравнений электрических цепей под сигналами понимаются токи, напряжения и т. д.
5. При прохождении по ветви сигнал умножается на передачу ветви.

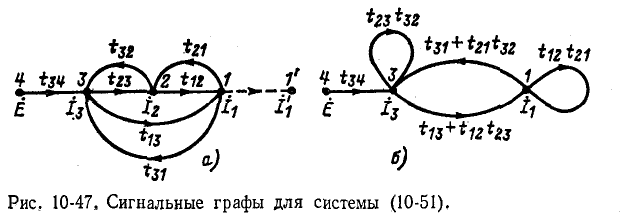
5.    Результирующий сигнал в узле равен сумме всех сигналов, приходящих в данный узел по ветвям, входящим в этот узел.

В соответствии с вышесказанным ток 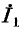представляет собой сигнал в вершине 1 графа на рис. 10-47, а, ток 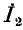— сигнал в вершине 2, ток 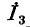— сигнал в вершине 3 и э. д. с. Ё — сигнал в вершине 4. Согласно первому уравнению системы (10-51) в вершину 1 должны входить ветвь с передачей 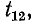выходящая из вершины 2, и ветвь с передачей 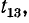выходящая из вершины 3 (рис. 10-47). Аналогичные рассуждения относятся и к остальным ветвям графа, изображенного на рис. 10-47, а.

Выше отмечалось, что для построения сигнального графа следует каждое уравнение разрешить относительно одной переменной. Очевидно, это можно сделать по-разному. Например, первое уравнение рассмотренной выше системы уравнений можно разрешить относительно 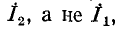второе уравнение — относительно 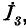третье — относительно 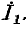В результате получится система уравнений, отличная по форме от системы (10-51), и соответственно сигнальный граф для такой системы будет отличен от графа на рис. 10-47, а.

Таким образом, для данной системы уравнений можно построить различные графы, но данному графу соответствует совершенно определенная система уравнений.

После построения сигнального графа для данной системы уравнений ее решение сводится к вычислению передачи сигнального графа.

Передачей сигнального графа от истока, откуда только выходят ветви графа, к стоку, куда только входят ветви графа, называется отношение сигнала в стоке к сигналу в истоке. Узел 4 графа на рис. 10-47, а является источником. Узел 1 не является стоком, но можно добавить узел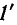 с сигналом 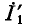и соединить его с узлом 1 ветвью с единичной передачей, что соответствует уравнению 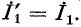Узел 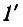является стоком, тогда передача от узла 4 к узлу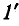

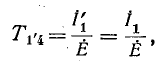
откуда 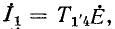т. е., зная передачу графа от узла 4 к узлу 1', можно определить ток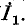

Ниже рассмотрены два метода нахождения передачи сигнального графа: 1) последовательным упрощением графа и 2) вычислением передачи по формуле Мейсона.

Метод упрощения сигнального графа основан на следующих правилах:

1. Параллельно соединенные ветви, направленные в одну сторону, заменяются одной ветвью, передача которой равна сумме передач параллельно соединенных ветвей (рис. 10-48, а).
2. Последовательно соединенные ветви, направленные в одну сторону, заменяются одной ветвью, передача которой равна произведению передач ветвей (рис. 10-48, б).
3. Если в точке соединения двух ветвей с передачам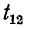и и 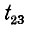имеется петля с передачей 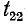(петля — это ветвь, выходящая из того же узла, куда она входит), то все эти три ветви заменяются одной ветвью с передачей (рис. 10-48, в)

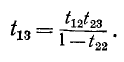
Указанные выше правила являются частными случаями общего правила устранения вершин. При устранении вершины графа устраняется и сигнал, соответствующий этой вершине, т. е. устранение вершины равносильно исключению переменной из системы уравнений. Вообще всякому

преобразованию графа соответствует определенное преобразование системы уравнений.

При устранении некоторой вершины (рис. 10-48, г) удаляются все ветви, входящие или выходящие из этой вершины. Передачи оставшихся ветвей (вблизи удаленного

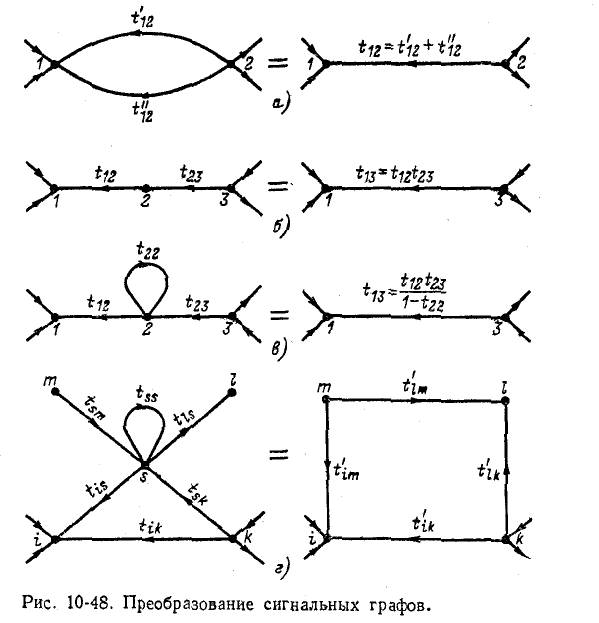
узла) соответствующим образом меняются. Если в исходном графе имеется ветвь, идущая из узла k в узел s с передачей 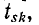и ветвь, идущая из узлаs в узел i с передачей 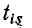(рис. 10-48, г), то новая передача ветви между узлами k и i вычисляется по формуле

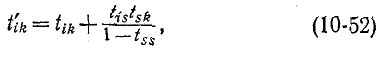
где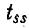— передача петли в вершине s.

Если в исходном графе отсутствует ветвь между узлами k и i, то“в формуле (10-52) следует положить 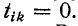Аналогично 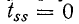при отсутствии петли в вершине s. В частном случае вершины i и к могут совпадать, что приведет к появлению петли в новом графе. Передачи 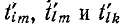находятся по формуле, аналогичной формуле (10-52).

В качестве примера применения формулы (10-52) устраним вершину 2 из графа на рис. 10-47, а. В результате получится граф, изображенный на рис. 10-47, б. Выражения для передач ветвей указаны на рисунке.

Далее можно удалить узел 3 из графа на рис. 10-47, б; получится граф, содержащий узлы 1 и 4, причем в узле 1 будет петля. Для удаления этой петли можно добавить ветвь с единичной передачей, как указано было ранее (пунктирная линия на рис. 10-47, а) и устранить узел 1. Окончательно получится граф, содержащий единственную ветвь с передачей 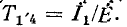Указанные преобразования предлагается выполнить в качестве упражнения, и результат сравнить с (10-57).

В графе на рис. 10-47, а узел 4 является истоком. Соответствующий ему сигнал (э. д. с. Ё) считается известным и находится только в правой части уравнений (10-51). Может возникнуть обратная задача определения э. д. с. Е, которую в этом случае необходимо перенести в левую часть уравнения, после чего узел 4 перестает быть истоком. Ветвь с передачей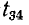 после такого преобразования будет входить в узел 4.

Операция изменения направления ветвей называется инверсией.

Рассмотрим сначала инверсию одной ветви, выходящей из истока i и входящей в узел k. Поскольку узел i является истоком, то соответствующий ему сигнал Xi находится только в правой части системы уравнений, т. е. нет уравнения, выражающего сигнал 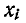через другие сигналы. Для k-ro узла такое уравнение имеет вид:

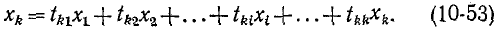
Определим из этого уравнения сигнал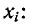

-

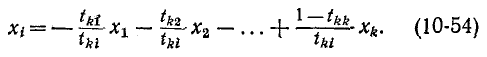
Уравнению (10-53) соответствует часть графа, показанная на рис. 10-49, а. После преобразования уравнения (10-53) сигнал узла k переходит в правую часть уравнения, т. е.

узел k становится истоком. Граф, соответствующий уравнению (Ю-54), показан на рис. 10-49, б. Сравнивая эти графы, получаем правило для инверсии ветви tkl\

1. устраняем петлю в узле k (если она имеется);
2. инвертируемую ветвь 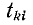заменяем ветвью с передачей 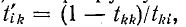имеющей противоположное направление;
3. концы ветвей, входивших в узел k, переносим в узел t, умножая передачи этих ветвей на —

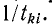
После инверсии ветви с передачей tki узел k становится истоком. В связи с этим можно инвертировать любую ветвь, выходящую из узла k, скажем, ветвь //*. В результате ока-

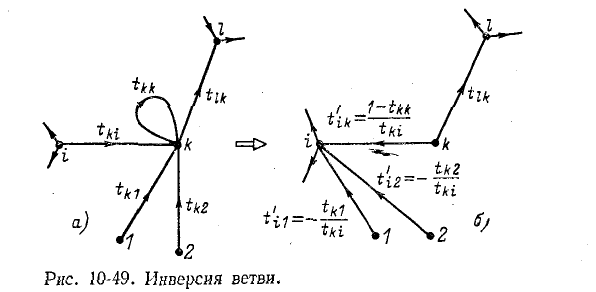
жется инвертированным путь 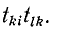Таким образом, используя приведенное выше правило, можно инвертировать путь, начинающийся в истоке.

Описанный выше метод является громоздким. Его целесообразно использовать лишь для предварительных упрощений и преобразований сигнальных графов. Более удобно вычислять передачу графа по формуле Мейсона.

Передача сигнального графа от истока к стоку

где А — определитель графа;

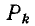— передача k-ro пути в графе от истока к стоку;

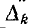— алгебраическое дополнение пути.

Суммирование выполняется по всем возможным путям. Путь в графе берется с учетом направления ветвей, т. е., идя от истока до стока, необходимо все время идти

в направлении стрелок. Передача пути равна произведению передач всех ветвей пути.

Определитель графа

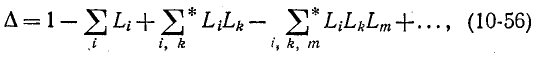
где 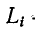— передача i-го контура, равная произведению передач всех ветвей контура. Контуры выбираются так, чтобы все ветви в контуре были направлены в одну сторону. Звездочки у знака сумм означают, что следует брать произведения величин двух, трех и т. д. некасающихся контуров.

Алгебраическое дополнение 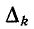вычисляется по той же формуле (10-56), но при этом следует учитывать во всех суммах лишь контуры, не касающиеся пути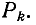
Пример 10-6. Вычислить передачу графа на рис. 10-47, а от узла 4 к узлу 1.

Поскольку все контуры графа касаются друг друга, то в соответствии с формулой {10-56) в выражении определителя необходимо учесть единицу и взятую со знаком минус сумму передач контуров, Следовательно, определитель графа

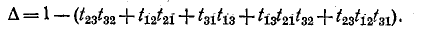
В графе на рис. 10-47, а имеются два пути от истока к стоку: 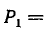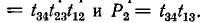Алгебраические дополнения этих путей равны единице, так как все контуры касаются их.

Теперь остается подставить выражения определителя, передач путей и их алгебраических дополнений в выражение (10-55) или в равенство

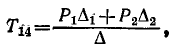
что дает

 

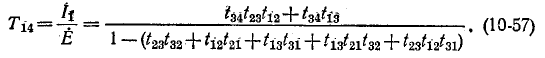
Построение сигнальных графов электрических цепей

Как указывалось ранее, для любой системы линейных уравнений можно построить сигнальный граф. При анализе электрических цепей в качестве такой системы уравнений можно взять уравнения или по законам Кирхгофа, или по методу контурных токов, или по методу узловых напряжений. Чтобы исключить промежуточную операцию составления уравнений, нужно найти метод построения графа по схеме электрической цепи. Ниже рассмотрены

правила построения графа для расчетов методами контурных токов и узловых напряжений.

Независимо от схемы электрической цепи уравнения по методу контурных токов имеют, например, для трех контуров, такой вид:

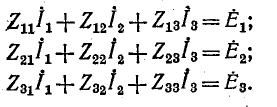
Перенесем все члены этих уравнений в правую часть. Прибавим к обеим частям первого уравнения 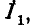второго 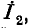третьего 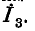В результате получаем систему уравнений:

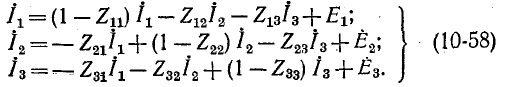
Этой системе уравнений соответствует сигнальный граф, показанный на рис. 10-50. Его можно построить, не записывая системы уравнений, при
любом числе контуров, имея в виду следующие свойства графа:

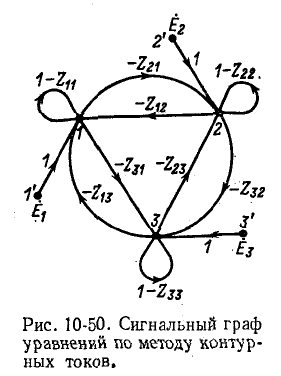
1. В k-м узле графа, соответствующем k-му контурному току 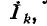имеется петля с передачей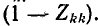
2. Между 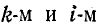узлами имеются две ветви. Одна с передачей 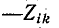направлена от узла k в узел i, другая с передачей 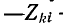— из узла i в узел k.
3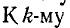 узлу подходит ветвь из узла с сигналом 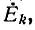имеющая единичную передачу.
По этим правилам легко построить сигнальный граф, не составляя системы уравнений. В
этом нет необходимости, так как сам сигнальный граф представляет собой геометрическую запись системы уравнений. Передачи ветвей графа вычисляются по тем же правилам, по которым вычисляются собственные и общие сопротивления контуров аналогично можно составить сигнальный граф для уравнений по методу узловых напряжений. Для случая трех узлов имеем такие уравнения:

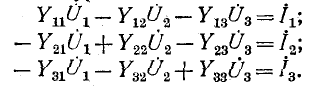
Преобразуя эти уравнения аналогично тому, как это делалось с уравнениями по методу контурных токов, получим:

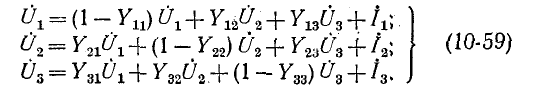
Полученные уравнения отличаются по структуре от уравнений (10-58) только знаками при общих проводимостях. Соответственно этому и правило составления графа будет отличаться тем, что знаки передач ветвей, соединяющих разные узлы, будут положительны. Конфигурация же графа не изменится.