Евклидово пространство - определение и свойства с примерами решения

Содержание:

Декартово произведение множества действительных чисел R само на себя состоит из всевозможных упорядоченных числовых пар. Это множество обозначают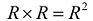

Понятие евклидова пространства в линейной алгебре. N-мерные векторы

Множество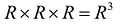

В общем случае А и В - это n-мерные векторы, т.е. 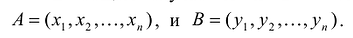Их скалярное произведение равно сумме попарных произведений их соответствующих координат, т.е. 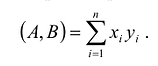. Длиной n-мерного вектора 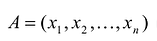называется число 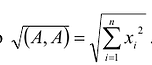Скалярное произведение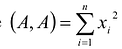называется скалярным квадратом вектора А и обозначается 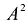. Поскольку скалярный квадрат является суммой квадратов координат вектора А, то его значение будет неотрицательным, причем 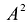= 0 тогда и только тогда, когда все координаты этого вектора равны нулю, т.е. вектор А - нулевой.

Пространство n -мерных векторов, в котором определена операция скалярного произведения, называется евклидовым пространством.

Теорема. Если А и В -это n -мерные векторы евклидова пространства, то справедливо неравенство:

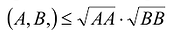
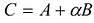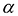Доказательство: Рассмотрим вектор , где - любое действительное число. Поскольку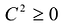, то на основании свойств скалярного произведения можно записать:

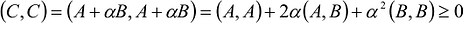
Если предположить, что 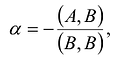-то справедливо следующее:

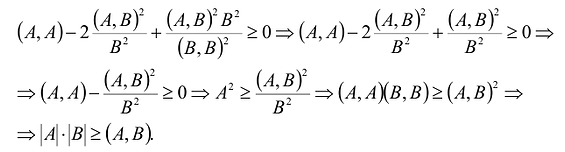
Доказанное неравенство называется неравенством Коши-Буняковского. Причем, равенство имеет место тогда и только тогда, когда векторы А и В линейно зависимы. В общем случае, угол между векторами А и В можно определить как решение уравнения:

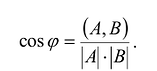
Таким образом, в евклидовом пространстве «-мерных векторов скалярное произведение любых двух векторов А и В равно:

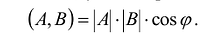
Теорема. Ненулевые п-мерные векторы А и В равны тогда и только тогда, когда угол между этими векторами равен нулю и длины их равны.

Доказательство:

Необходимость:

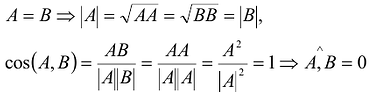
Достаточность:

Пусть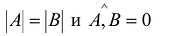

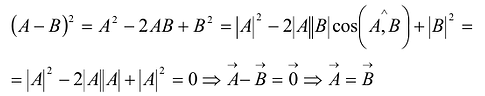
Коллинеарные векторы

Два ненулевых n-мерных вектора А и В называются коллинеарными, если угол между ними равен 0 или .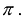

Если А,В = 0, то коллинеарные векторы называются сонанравлепными или одинаково направленными ().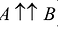

Если 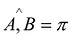, то коллинеарные векторы называются противоположно направленными ().

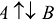Если условие коллинеарности между векторами А и В не выполняется (т.е. 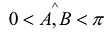), то такие вектора называются неколлинеарными.

Теорема. Ненулевые векторы А и В коллинеарны тогда и только тогда, когда найдется такое ненулевое число к, что В = кА.

Доказательcmво:

Необходимость:

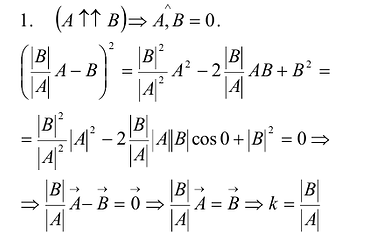
2. 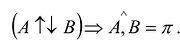. Для этого случая аналогично доказывается, что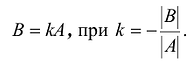

Достаточность: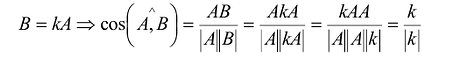

Число 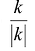имеет только два значения: {-1,1}. Это означает, что 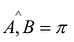или 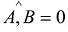, соответственно. Таким образом, вектора A и В коллинеарны.

• Заказать решение задач по высшей математике

Размерность и базис векторного пространства

Определение. Вектор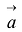 называется линейной комбинацией векторов 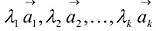векторного пространства R, если он равен сумме произведений этих векторов на произвольные действителъные числа:

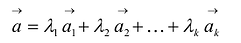, (8.1) где 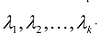какие угодно действительные числа.

Определение. Векторы 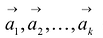векторного пространства R называются линейно зависимыми, если существуют, такие числа 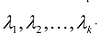, не равные одновременно нулю:

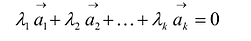(8-2)

В противном случае векторы 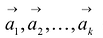называются линейно независимыми.

Из приведенных выше определений следует, что векторы 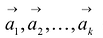линейно независимы, если равенство 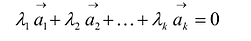справедливо лишь при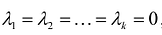, и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 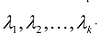отлично от нуля.

Можно показать, что если векторы 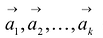линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы. В противном случае векторы 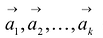называются линейно независимыми.

Из приведенных выше определений следует, что векторы 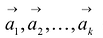линейно независимы, если равенство (8.2) справедливо лишь при 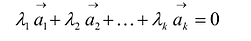, и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 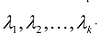отлично от нуля.

Примером линейно независимых векторов являются два неколлинеарных, т.е. не параллельных одной прямой, вектора 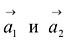на плоскости. Действительно, условие (8.2) 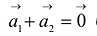будет выполняться лишь в случае, когда 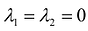, ибо если, например, 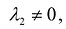, то 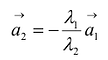и векторы 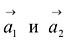коллинеарны. Однако любые три вектора плоскости линейно зависимы.

Отметим некоторые свойства векторов линейного пространства.

• I. Если среди векторов 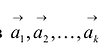имеется нулевой вектор, то эти векторы линейно зависимы.
• II. Если часть векторов 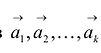являются линейно зависимыми, то и все эти векторы — линейно зависимые.

Определение. Линейное пространство R называется п-мернмму если в нем существует п линейно независимых векторов, а любые из (n +1) векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число п называется размерностью пространства R и обозначается dim(R).

Определение. Совокупность п линейно независимых векторов n -мерного пространства R называется базисом. Справедлива следующая теорема.

Теорема. Каждый вектор X линейного пространства R ложно представить и притом единственным способом в виде линейной комбинации векторов базиса :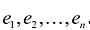

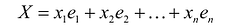
Это равенство называется разложением вектора X по базису 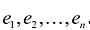, а числа 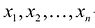— координатами вектора х относительно этого базиса. В силу единственности разложения каждый вектор однозначно может быть определен координатами в некотором базисе.

Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, - противоположные по знаку координаты.

Теорема. Если 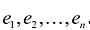- система линейно независимых векторов пространства R и любой вектор X линейно выражается через 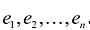то пространство R является n-мерным пространством 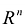, а векторы 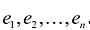- его базисом.

Базисом векторного пространства 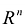называется любая независимая система линейно независимых п -векторов этого пространства, количество которых равно п, т.е. выбор системы базисных векторов векторного пространства 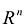неоднозначен, и может быть осуществлен большим числом способов.

Нередко приходится встречаться с заменой переменных, при которой старые переменные линейно выражаются через новые, например, при переходе от одного базиса пространства 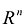к другому. Такую замену переменных называют обычно их линейным преобразованием.

Линейным преобразованием переменных называется выражение системы переменных 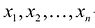через новую систему переменных 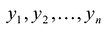с помощью линейных однородных функций:

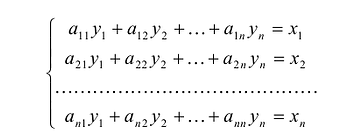
Линейное преобразование вполне определяется таблицей размером nхn, составленной из коэффициентов при 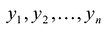. Такая таблица, составленная из элементов 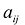называется матрицей 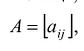а само преобразование представляет собой пример матричной операции. Понятие матрицы требует более детального рассмотрения, что и будет сделано в следующем разделе.