Естественный и векторный способы определения движения точки в теоретической механике

Содержание:

Естественный и векторный способы определения движения точки:

При естественном способе определения движения точки должны быть заданы ее траектория н расстояние как некоторая непрерывная однозначная функция времени

Естественный способ определения движения

Изучение движения точки без учета приложенных к ней сил составляет задачу кинематики точки. Кинематика точки является основным и вместе с тем наиболее простым отделом кинематики.

Чтобы определить движение точки, необходимо знать, какое положение она занимает в данное мгновение и как это положение изменяется с течением времени.

Определить положение и движение точки относительно какой-либо системы отсчета можно различными способами. Познакомимся с одним из этих способов, называемым естественным способом определения движения точки, или способом определения движения точки по заданной траектории.

Движущаяся точка в различные мгновения занимает различные положения относительно системы отсчета. Геометрическое место всех последовательных положений движущейся точки относительно данной системы отсчета называют траекторией точки, или, коротко, траекторией.

Движение точки называют прямолинейным, если траектория — прямая линия, и криволинейным, если траектория —не прямая, а какая-либо кривая линия. Эта кривая может быть плоской (например, парабола) или не плоской кривой (например, винтовая линия).

Траектория точки может быть известна (задана) еще до того, как началось движение точки. Так, например, полотно железной дороги является траекторией поездов, траектории (орбиты) искусственных спутников вычисляют еще до начала их полета.

Пусть точка движется по некоторой траектории (или, как говорят, описывает траекторию) и в данное мгновение занимает положение M (рис. 77). Положение точки M известно, если дано ее расстояние s = AM (измеренное по траектории) от точки А, принятой зa начало отсчета, причем расстояние считают положительным по одну сторону от. точки А и отрицательным—по другую. Положительное направление отсчета выбирают в зависимости от условий задачи. Так, например, местонахождение поезда известно, если известна железная дорога и расстояние s поезда от какой-либо станции; разумеется, при этом надо знать, по какую сторону от станции находится поезд на данном расстоянии s.

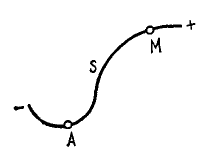
Расстояние s движущейся точки с течением времени изменяется, оно является функцией времени

s=s(t).                (51)

Эта функция однозначна, так как точка в каждое мгновение занимает на траектории только одно положение, а не несколько.

Эта функция непрерывна, так как точка не может перейти из одного положения на траектории в другое, минуя промежуточные.

Кроме того, функция (51) должна быть дважды дифференцируемой; прочие случаи в нашем курсе не рассмотрены, как не имеющие практического значения.

Функцию s(t) называют кинематическим уравнением движения точки по траектории, или законом движения.

Движение точки задано, если положение точки может быть определено в любое мгновение. Чтобы задать движение точки естественным способом, необходимо и достаточно задать траекторию точки и уравнение движения точки по траектории. Так, например, если известно, что поезд идет из Москвы в Курск (траектория — Московско-Курская ж. д.), следуя закону s=100t, где s—расстояние от Москвы в километрах, t—время, протекшее после отхода поезда из Москвы, выраженное в часах, то местонахождение поезда
в любой момент времени может быть определено, и движение поезда является заданным в естественной форме.

Алгебраическая величина скорости выражается первой производной от расстояния по времени: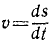 

Алгебраическая величина скорости. В каждое мгновение движущаяся точка занимает одно и вполне определенное положение на своей траектории. Но с течением времени положение точки меняется. Чтобы охарактеризовать изменение положения точки на ее траектории в любое данное мгновение, введем  понятие алгебраической величины скорости точки.

Подставим в (51) какое-либо частное значение времени t и вычислим значение s, соответствующее этому значению t. Тем самым мы определим положение точки M на ее траектории в это мгновение. Через промежуток времени Δt положение точки изменится на Некоторую величину Δs. Предположим, что точка M в течение времени Δt движется по своей траектории в одном направлении (не совершает возвратных движений). Величину Δs мы назовем приращением расстояния точки M за время Δl и определим ее по приращению функции (51):

∆s=s(t + Δt)—s(t).

Отношение приращения расстояния точки к соответствующему промежутку времени называют средней скоростью точки:

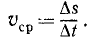     (52)

Если мы будем уменьшать промежуток времени, оставляя неизменным начало этого промежутка, то отношение (52) будет стремиться к некоторому пределу, называемому алгебраической величиной скорости точки в данное мгновение, или, коротко, алгебраической скоростью точки:

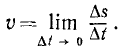
В правой части равенства мы имеем производную от расстояния по времени. Следовательно, алгебраическая величина скорости выражается первой производной от расстояния по времени:

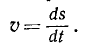     (53)

Итак, если движение точки задано в естественной форме, то для определения алгебраической величины скорости нужно взять первую производную по времени от расстояния, выражаемого законом движения точки. Если знак производной положителен, то, следовательно, расстояние возрастает, и точка M движется по траектории в том направлении, которое мы приняли за положительное при отсчете расстояний s; при отрицательной производной точка движется в обратную сторону. Таким образом, формула (53) определяет величину скорости и показывает, в какую сторону траектории движется точка. Эту формулу широко применяют при решении задач. Размерность скорости равна размерности длины, деленной на размерность времени:

[υ] = L¹T^-1.

В зависимости от условий задачи скорость измеряют в километрах в час (км/ч), или км/ceκ, или мм/сек и т.п.

При естественном способе определения движения закон движения точки может быть задан графиком расстояния

Графики

При изучении движения точки по траектории часто пользуются графическим методом. Графический метод при естественной форме задания движения особенно удобен в тех случаях, когда за видимость расстояния s от времени t не может быть выражена аналитически соотношением (51), но могут быть определены (например, экспериментально) расстояния s₁, s₂, s₃, ..., s_n точки M, соответствующие отдельным мгновениям t₁, t₂, t₃, ..., t_n.

Откладывая по «оси времени» (по оси абсцисс) (рис. 78, а) значения времени, а по «оси расстояний» (по оси ординат)—расстояния s, соответствующие этим мгновениям, мы построим отдельные точки графика, соединяя которые, получим кривую (рис. 78, а, б), называемую графиком расстояний, или графиком движения. Движение точки определено, если даны ее траектория и график движения.

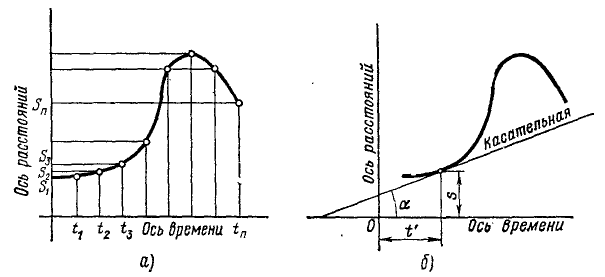
Рис. 78

В таком случае для определения алгебраической скорости применяют методы графического дифференцирования, изучение которых не входит в нашу программу. По одному из этих методов для определения скорости в какое-либо мгновение t' нужно измерить тангенс угла между осью времени и касательной к графику расстояний, проведенной в точке, абсцисса которой равна t' (рис. 78, б). Тангенс угла наклона касательной к оси абсцисс равен 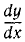. В нашем случае ось расстояний—это ось у, а ось времени — это ось х, следовательно,

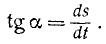
Можно построить график зависимости скорости и от времени t. Такой график называют графиком скорости, или тахограммой.

Графический метод широко применяют, в частности, при изучении различных механизмов и машин.

Задача №1

Точка M совершает прямолинейное движение по закону s=AM =2 sin πf+1. Определить расстояние точки, величину и направление ее скорости через каждые 1/4 сек от начала движения и построить по точкам график движения (рис. 79, а).

Решение. Дифференцируя уравнение движения, получим

υ=6,28 cos лt.

Подставляя сюда и в уравнение движения частные значения времени (t=0 сек, 0,25 сек, 0,5 сек), найдем следующие частные значения s и υ:

t	0,00	0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00
s	+1,00	+2,41	+3,00	+2,41	+1,00	-0,41	-1,00	-0,41	+1,00
υ	+6,28	4,43	0,00	-4,43	-6,23	-4,43	0,00	+4,43	+6,28

Если за положительное направление на траектории принято направление вправо от начала отсчета (от точки A), то в начальное мгновение точка M находилась справа от А на расстоянии 1 см, алгебраическая величина скорости в это мгновение тоже положительна — движение происходит вправо.

Затем скорость уменьшается и в мгновение t = 0,5 сек обращается в нуль. C этого мгновения точка M начинает двигаться влево, алгебраическая скорость становится отрицательной, расстояние пока остается положительным, но уменьшается. S какое-то мгновение, находящееся между 1 сек и 1,25 сек, точка M проходит через начало отсчета А и расстояние равно 0, но затем становится отрицательным. Точка М продолжает двигаться влево, но скорость ее по абсолютной величине уменьшается и в мгновение t=1,5 сек меняет знак, следовательно, меняется направление движения, но расстояние остается отрицательным, так как точка M находится по отрицательную сторону от точки А. В мгновение t=2 сек точка возвращается ι начальное положение, обладав скоростью, равной начальной скорости, и с этого мгновение движение повторяется в том же порядке.

Для построения графика расстояний нарисуем две взаимно перпендикулярные оси (ось времени и ось расстояний) и нанесем точки, абсциссы которых (в каком-либо масштабе) равны 0; 0,25; 0,50, а ординаты (тоже в каком-либо масштабе) соответствующие им расстояния s (рис. 79, б). Соединяя затем плавной кривой вс эти точки, получим график расстояний (рис. 79, в).

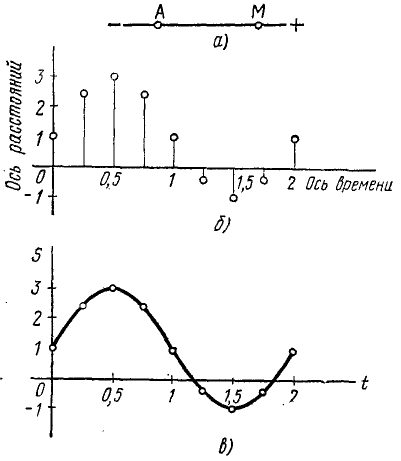
Рис. 79

График расстояний не зависит от траектории, и если бы точка M двигалась, следуя тому же закону s = 2 sin πt+1, по какой-либо другой траектории, т< график расстояний остался бы тот же.

При векторном способе определения движения точки должен быть задан ее радиус-вектор как функция времени

Задание движения точки в векторной форме. Положение точки M по отношению к какой-либо системе отсчета может быть определено радиусом-вектором 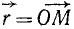, проведенным из центра О данной системы отсчета к точке M (рис. 80, а).

Во время движения точки радиус-вектор ее изменяется. Чтобы определить движение точки, нужно задать ее радиус-вектор для каждого мгновения, т. е. выразить его в виде некоторой векторной функции времени

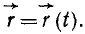      (54)

 Эта функция должна быть однозначной и непрерывной. Такой способ определения движения точки называют векторным.

Пусть положение движущейся точки в мгновение, принятое нами за начальное, определяется радиусом-вектором 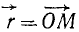(рис. 80,6). Через промежуток времени Δ t точка переместилась и заняла другое положение, которое мы назовем конечным для данного отрезка времени, и радиус-вектор ее стал 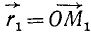. Проведем вектор 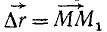из точки M в точку M₁ Как видно из чертежа,

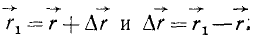
Вектор 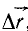, проведенный из начального положения точки в конечное, определяет изменение положения точки в данной системе отсчета и называется перемещением точки.

Вектор 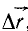отмечает положения точки только в начальное и конечное мгновения интервала времени Δt, но не дает возможности определить положение точки в промежуточные мгновения этого интервала времени. За бесконечно малый отрезок времени перемещение точки тоже бесконечно мало. Оно выражается бесконечно малым вектором, называемым элементарным перемещением. Элементарное перемещение точки соответствует ее действительному передвижению за данный бесконечно малый промежуток времени.

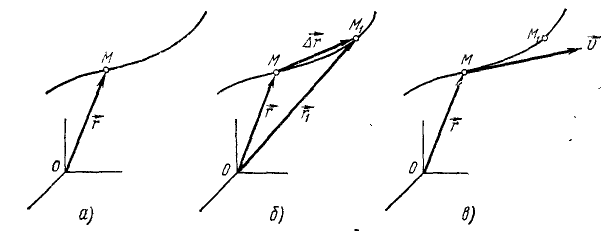
Рис. 80

Перемещение—пространственная мера движения точки и выражается в единицах длины. Оно характеризует передвижение точки только с геометрической стороны, вне зависимости от времени, и, κаκ и траектория точки, является геометрическим понятием.

Но между перемещением точки за какой-либо промежуток времени и траекторией, описанной точкой за то же время, есть существенное различие: перемещение—это вектор, соединяющий положения точки в начальное и конечное мгновения данного промежутка времени, а траектория—совокупность всех положений, которые занимала точка в различные мгновения этого промежутка времени. Так, например, если теплоход вышел из Москвы, по каналу прошел в Волгу, спустился по Волге до Волго-Донского канала, перешел в Дон и доплыл до Ростова, то перемещение его изобразится вектором, проведенным из Москвы в Ростов по хорде земного шара, а траекторией является вся пройденная теплоходом трасса.

К понятиям траектории и перемещения близко примыкает понятие «путь», с которым мы сейчас ознакомимся. Пусть в начальное мгновение точка занимает на своей траектории положение M (рис. 81, а), а через промежуток времени Δt—конечное положение M_n. Вектор 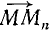является перемещением точки за время Δt. Разбив интервал времени Δt на части, мы отметим промежуточные положения точки (M_l, M₂, M₃, ...) и все их последовательно соединим хордами. Мы получим ломаную MM₁M₂M₃.. .M_n (рис. 81, б). Чем меньше отрезки времени, на которые мы разбили Δt , тем ближе ломаная соответствует траектории точки и тем меньше длина ломаной отличается от длины дуги, пройденной точкой за время Δt. Назовем путем точки предел суммы абсолютных значений элементарных перемещений точки за данный конечный промежуток времени. Следует обратить внимание на то, что для получения пути мы взяли предел арифметической суммы абсолютных значений (модулей) элементарных перемещений, а не геометрической суммы этих перемещений. Если бы эти перемещения мы складывали геометрически (рис. 81, в), то получили бы перемещение .

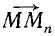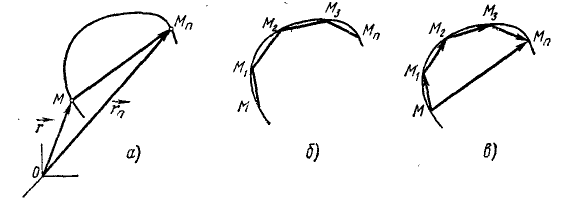
Рис. 81

Путь не надо смешивать с расстоянием s. Отличие заключается в следующем: путь всегда положителен и с течением времени возрастает, расстояние же определяется величиной и знаком « + » или «—» и с течением времени может увеличиваться или уменьшаться в зависимости от направления движения точки. Если точка (см. рис. 81), двигаясь по траектории из пункта М, достигла пункта М_n, а затем вернулась в пункт M₃, то путь точки равняется сумме дуг MM_n+M_nM₃, а расстояние от точки M (если этот пункт принят за начало отсчета расстояний) равно длине дуги MM₃, причем ему cледует приписать знак «+» или «—» в зависимости от того, какое направление принято за положительное при отсчете расстояний.

Скорость выражается пределом отношения элементарного перемещения к соответствующему промежутку времени, т. е. первой производной от радиуса-вектора по времени:

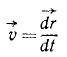
Вектор скорости

Для характеристики движения точки не только в пространстве, но и во времени возьмем отношение перемещения точки ко времени, в течение которого происходило это перемещение:

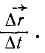
Такое отношение является вектором, направленным по вектору перемещения точки, потому что от деления на скалярную величину вектор не меняет направления. Будем уменьшать промежуток времени ∆t, оставляя неизменным начало этого промежутка. Тогда вектор 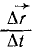 будет приближаться к определенному вектору 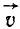как к своему пределу:

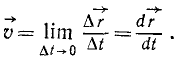      (55)

Вектор 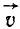выражает скорость точки и характеризует с кинематической (а не только с геометрической) стороны изменение положения точки в данное мгновение.

Следовательно, скорость точки—это пространственно-временная мера движения, характеризующая изменение положения точки в данное мгновение в данной системе отсчета, выражающаяся пределом отношения элементарного перемещения к соответствующему промежутку времени, т. е. первой геометрической производной от радиуса-вектора по скалярному аргументу—времени.

Определим направление 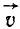. Вектор  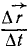направлен по хорде траектории в сторону движения точки. Пусть промежуток времени Δt стремится к нулю, но начало этого промежутка остается неизменным. Одновременно хорда (точнее, секущая) стремится к касательной, следовательно, вектор 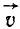в данной точке траектории направлен по касательной к траектории в сторону движения точки (см. рис. 80, в).

Заметим, что всякую кривую, являющуюся геометрическим местом концов переменного вектора, выходящего из одной точки и выраженного функцией времени, называют годографом вектора. Следовательно, траектория точки является годографом ее радиуса-вектора.

Ускорение выражается пределом отношения изменения скорости к соответствующему промежутку времени, т. е. первой производной от вектора скорости по времени:

• Заказать решение задач по теоретической механике

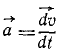
Вектор ускорения

При равномерном прямолинейном движении точки скорость сохраняет свою величину и свое направление. При неравномерном и криволинейном движении скорость изменяется по величине и по направлению. Изменение величины и направления скорости происходит с течением времени. Пространственно-временной мерой изменения скорости точки в данное мгновение ив данной системе отсчета, является ускорение точки.

Пусть скорость точки в некоторое мгновение изображается вектором 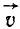(рис. 82, а), а через промежуток времени Δt она изменилась и стала 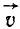. Изменение скорости за время Δt изобразится разностью этих векторов (рис. 82, б):

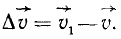
Возьмем отношение вектора ∆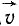 изменения скорости ко времени ∆t, в течение которого это изменение произошло, и будем уменьшать ∆t, сохраняя начало этого промежутка, тогда вектор 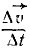будет изменяться, приближаясь к определенному вектору 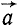, как к своему пределу. Этот предельный вектор  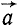изображает ускорение точки. Следовательно, ускорение точки выражается пределом отношения изменения вектора скорости к соответствующему промежутку времени при стремлении этого промежутка к нулю:

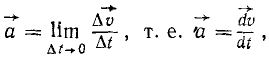        (56)

или 

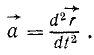        (57)

Рис. 82

Размерность ускорения—это размерность скорости, деленной на размерность времени, или, что то же, размерность длины, деленной на квадрат размерности времени:

[α] =L¹T^-2.

Единицей ускорения может быть км/сек², м/сек² и т. п.

Формулы (56) и (57) часто применяют при выводе различных теорем кинематики и динамики, но ими не всегда удобно пользоваться при практических подсчетах и при решении различных технических задач. Более удобные для практики формулы будут выведены в следующих параграфах.

Метод Роберваля построения касательных к кривым

Задача №2

Построить касательную к эллипсу.

Решение. Рассмотрим эллипс как траекторию точки M (рис. 83, а). Приняв фокус Ф₁ за начало системы отсчета, мы можем считать эллипс годографом радиуса-вектора 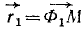, выраженного в функции времени. Скорость точки M всегда направлена по касательной к траектории и, чтобы найти эту касательную, предположим, что мы разложили вектор скорости на две составляющие, одна из которых выражает быстроту изменения величины радиуса-вектора, следовательно, направлена по Φ₁M и по величине равна первой производной от модуля радиуса-вектора по времени 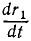. Назовем ее радиальной компонентой скорости и отложим
вдоль радиуса-вектора в виде произвольного отрезка MP₁, так как величина этой компоненты неизвестна. Вторая составляющая скорости направлена перпендикулярно к первой и характеризует быстроту поворота радиуса-вектора 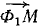. Эту компоненту вектора скорости называют трансверсальной. Изобразим ее отрезком P₁T₁ произвольной длины, перпендикулярным к MP₁, так как величина этой компоненты также неизвестна. Если бы отрезки MP1 и P1T1 были нам известны, то скорость точки M изобразилась бы вектором MT₁ и мы нашли бы направление касательной к эллипсу в точке М.

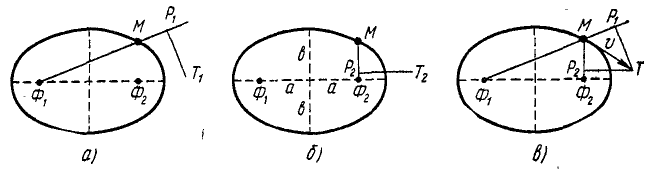
Рис. 83

Примем теперь за начало отсчета фокус Ф₂ (рис. 83, б). Тогда эллипс станет годографом радиуса-вектора 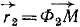, радиальная компонента скорости будет направлена по радиусу-вектору и по величине равна 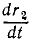. Припомним, что арифметическая сумма расстояний точки М, описывающей эллипс, от фокусов есть величина постоянная:

r₁+r₂ = const.

Дифференцируя это равенство по времени, мы найдем, что величины радиальных компонент скорости на рис. 83, а и б равны между собой:

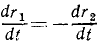
Знак минус показывает, что если увеличивается один радиус-вектор, то одновременно уменьшается другой и, как видно, на такую же величину. Поэтому на рис. 83, б мы отложим от M к Ф₂ отрезок MP₂ = MP₁, а затем от точки P₂ перпендикулярно к MΦ₂—отрезок P₂T₂, представляющий трансверсальную компоненту скорости. Величина этого отрезка нам неизвестна, поэтому неизвестно и направление касательной MT₂.

Но если мы соединим оба чертежа вместе, то получим (рис. 83, в) точку T на пересечении перпендикуляров P₁T и P₂T. Отрезок MT в некотором масштабе изображает скорость точки М, а его направление дает нам касательную.

В эпоху, предшествующую открытию дифференциального и интегрального исчислений, проблема построения касательных к кривым имела исключительное значение (см. также стр. 227). Метод, примененный нами к решению этой задачи, был предложен Робервалем и основан на сделанном им открытии, что скорость точки всегда направлена по касательной к траектории.