Энергия в электрических цепях

Содержание:

Энергия в электрических цепях и ее прямое и обратное преобразование в механическую энергию:

В современной электротехнике используются процессы прямого и обратного преобразования электрической энергии — энергии электромагнитного поля —в другие виды энергии. В большинстве электротехнических устройств распределение энергии электромагнитного поля между электрическим и магнитным полями таково, что одним из этих полей можно пренебречь. Поэтому далее теория преобразования энергии электрического поля системы заряженных тел и энергии магнитного поля контуров с токами излагается раздельно применительно к наиболее важному преобразованию в механическую энергию.

Силы, возникающие в этих полях, используются для создания не только преобразователей энергии, но и измерительных приборов различных систем, а также служат для управления движением заряженных частиц, что широко используется в различных электротехнических устройствах — электронных осциллографах, различных вакуумных и ионных приборах, ускорителях различных систем, установках для нанесения различных покрытий, а также в новых прямых преобразователях тепловой энергии в электрическую.

Энергия системы заряженных проводящих тел

Пусть в диэлектрической среде с постоянной проницаемостью ε находятся n неподвижных проводящих тел (рис. 2. 1); потенциал каждого из тел ϕ_k заряд Q_k, где k = 1, 2, ..., п.

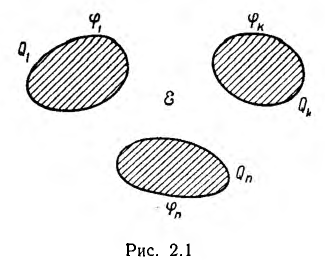
Для сообщения зарядов этой системе тел они подключаются к источникам электрической энергии; по соединительным проводам пойдут токи, прекращающиеся с окончанием зарядки.

Работа, совершаемая источниками, идет на сообщение зарядов телам системы, нагрев соединительных проводов и образование магнитного поля. Энергия, запасаемая в магнитном поле при возрастании тока, возвращается источникам при убывании тока, за исключением излученной в окружающее пространство, так как провод с изменяющимся током представляет собой антенну. Энергия, затраченная на сообщение зарядов, запасается в системе; нагрев и излучение являются потерями.

Так как величина энергии системы определяется потенциалами и зарядами тел и не зависит от скорости зарядки, для облегчения расчета предполагается, что зарядка системы совершается бесконечно медленно, т. е. токи зарядки бесконечно малы и постоянны. Это позволяет пользоваться зависимостями, установленными для электростатического поля, и пренебречь потерями и энергией магнитного поля, так как энергия тепловых потерь и энергия магнитного поля, пропорциональные квадрату тока, будут бесконечно малыми второго порядка, а излучение при постоянном токе отсутствует.

Тогда работа А источников равна энергии W, запасенной в системе заряженных тел. При возрастании на величину dq_k промежуточного значения заряда q_k тела k, с промежуточным значением потенциала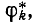

Для всей системы тел элементарная работа источников

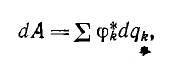
а вся энергия, запасенная в системе,

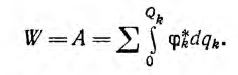
Потенциал каждого из тел связан с зарядами всех тел линейной зависимостью:

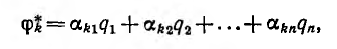
где 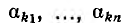— постоянные.

Согласно закону сохранения энергии, работа, затраченная на создание энергии системы, не зависит от порядка сообщения заряда отдельным телам системы. Если для расчета принять, что заряды всех тел изменяются пропорционально друг другу:

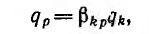
где 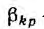— постоянные, то потенциал тела

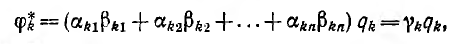
где 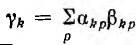— величина постоянная.

Подстановка равенства 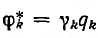в выражение для энергии даст

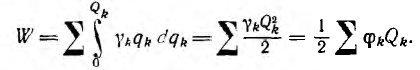
В этом выражении для энергии под 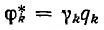понимаются значения потенциала и заряда по окончании зарядки.

Для уединенного тела

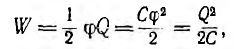
где С = Q/ϕ — емкость тела.
Для конденсатора, т. е. системы из двух тел 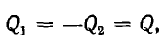напряжение U = ϕ₁ — ϕ₂ и энергия

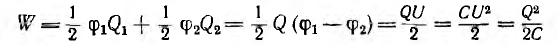
является квадратичной функцией заряда Q или напряжения U.

Энергия системы из двух конденсаторов, связанных взаимоемкостью, заряды которых определены выражениями (1.2),

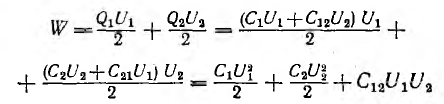
состоит из суммы собственных энергий каждого из конденсаторов и взаимной энергии 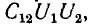зависящей от расположения конденсаторов. Взаимная энергия может иметь разный знак; поэтому энергия системы будет больше суммы собственных энергий конденсаторов при совпадении знаков собственного и взаимного зарядов или меньше — при противоположных знаках этих зарядов. Однако суммарная энергия системы заряженных конденсаторов всегда положительна.

Энергия системы из нескольких конденсаторов, состоящая из суммы собственных и взаимных энергий конденсаторов,

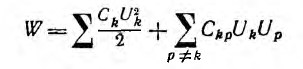
также всегда положительна. Энергия измеряется в джоулях (дж).

Энергия нелинейного конденсатора

Энергия линейного конденсатора 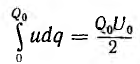с зарядом Q₀ и О напряжением U₀ равна площади заштрихованного треугольника на кулонвольтной характеристике (рис. 2.2, а).

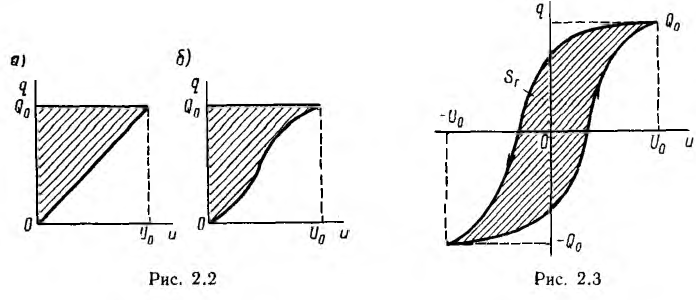
Работа источника, затраченная на зарядку нелинейного конденсатора и равная запасенной в нем энергии, определяется заштрихованной площадью, также ограниченной кулонвольтной характеристикой (рис. 2.2, б). Эта площадь может быть больше, равна или меньше площади треугольника 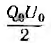в зависимости от вида характеристики и от значения напряжения U0, т. е. энергия нелинейного конденсатора не определяется конечными значениями Q₀ и U₀.
При периодическом изменении напряжения в пределах от U₀ до —U₀ на нелинейном конденсаторе в нем проявляется диэлектрический гистерезис. Если петля гистерезиса построена в координатах q и u (рис. 2.3), то потеря энергии за один цикл

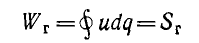
равна площади петли гистерезиса. Эти потери, превращающиеся в тепло, в большинстве современных сегнетоэлектриков пока еще значительны. В настоящее время ведется большая работа по устранению этого недостатка.

Распределение энергии электрического поля

Энергия электрического поля всегда распределена в пространстве, занятом полем. Энергия плоского конденсатора, поле которого однородно,

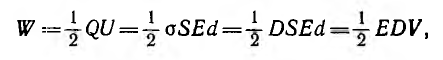
где Q —поверхностная плотность заряда, равная смещению D; V = Sd — объем, занятый полем.
Энергия в единице объема — плотность энергии —

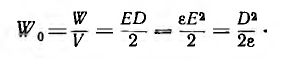
В случае неоднородного поля эти выражения могут быть использованы для бесконечно малого объема dV, в пределах которого поле может считаться однородным. Для конечного объема V энергия поля

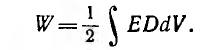
Эти формулы, выведенные для однородной изотропной среды, где векторы Е и D совпадают по направлению, могут быть записаны и так:

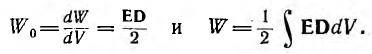
В таком виде выражение для энергии было постулировано Максвеллом для любых линейных и нелинейных сред и полей, как угодно изменяющихся во времени и пространстве. Это обобщение, используемое в теории электромагнитного поля, подтверждается совпадением выводов этой теории с опытом.

Взаимные преобразования энергии электрического поля и механической энергии

В системе подвижных заряженных тел энергия электрического поля изменяется, преобразуясь в другие виды энергии, в том числе в механическую. Если пренебречь тепловыми потерями и излучением, что теоретически справедливо при бесконечно медленном движении тел, то, согласно закону сохранения энергии, работа внешних источников 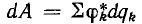равна сумме изменения энергии системы dW и механической работы dA_Mex:

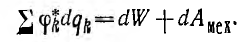
Отдельные члены этого равенства могут иметь различные знаки в зависимости от характера преобразования энергии — электрической в механическую (двигатели) или механической в электрическую (генераторы).
Известно, что состояние системы тел, как механической системы, может быть описано с помощью обобщенных геометрических координат X, число которых равно числу степеней свободы. В соответствии с обобщенными координатами вводятся совпадающие с ними по направлению обобщенные силы F, умножение которых на изменение обобщенной координаты дает механическую работу, совершаемую при «перемещении» по обобщенной координате, так что

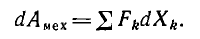
Если обобщенной координатой является обычная координата, то обобщенной силой — обычная сила; если X — угол поворота, то F — вращающий момент и т. п.

Пусть в рассматриваемой системе заряженных тел изменяется лишь одна из обобщенных координат, тогда основное соотношение примет вид

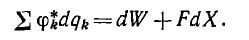
Это равенство, справедливое при любых соотношениях между зарядами и потенциалами тел, легко может быть исследовано лишь в двух частных случаях, рассматриваемых далее.

1. Если система отключена от источников, то заряды тел не изменяются (dq_k =0) и

откуда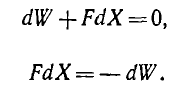

Это означает, что механическая работа в системе совершается за счет уменьшения энергии, запасенной в ней. В реальных условиях механическая работа будет меньше энергии, отданной системой, так как часть этой энергии идет на покрытие неизбежных потерь.

Итак, можно сделать общий вывод, что система, отключенная от источников, всегда стремится занять положение, соответствующее возможному для этой системы минимуму ее энергии.

2. Для системы заряженных тел, подключенных к источникам постоянных потенциалов (ϕ_k = const), из выражения энергии

следует, что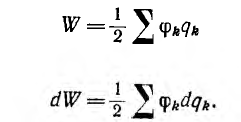

Тогда основное соотношение принимает вид:

откуда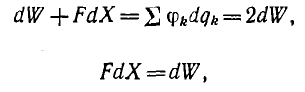

т. e. при совершении системой механической работы энергия системы возрастает на такую же величину, а работа, совершенная источниками и равная сумме механической работы и увеличения энергии, вдвое больше.

Следовательно, система, подключенная к источникам с постоянными потенциалами, всегда стремится занять положение, соответствующее возможному для этой системы максимуму ее энергии, т. е. максимуму зарядов.

Так как в реальной системе может быть сосредоточена лишь конечная энергия, то и в случае 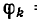= const система не может служить для непрерывного преобразования энергии электрического поля в механическую.
Из приведенных соотношений могут быть вычислены обобщенные силы, действующие на тела, находящиеся в электрическом поле. При постоянстве зарядов обобщенная сила

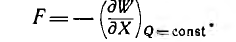
Здесь взята частная производная, так как в рассматриваемом случае изменение энергии соответствует изменению лишь одной из обобщенных координат.
При постоянстве потенциалов обобщенная сила

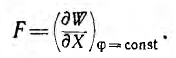
Это выражение отличается от приведенного выше. Однако результаты вычисления по этим формулам всегда совпадают, так как сила в данный момент определяется значениями зарядов и потенциалов тел в этот момент и не зависит от характера их изменения в дальнейшем.

Силы в электрическом поле действуют не только на проводящие тела, но и на диэлектрические, если их проницаемость отличается от проницаемости окружающей среды. Это объясняется возникновением с обеих сторон поверхности раздела разноименных зарядов, разных по величине; силы определяются алгебраической суммой этих зарядов.
Таким образом, силы в электрическом поле всегда проявляются у поверхности раздела различных сред: диэлектрик — проводник и диэлектрик —диэлектрик.

Вольтметр электростатической системы

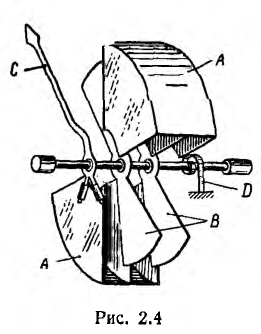
Примером системы двух заряженных тел может служить вольтметр электростатической системы (рис. 2.4). Он состоит из соединенных между собой неподвижных пластин А и укрепленных на оси подвижных пластин В. С осью прибора связана стрелка С, перемещающаяся по шкале. Под действием измеряемого напряжения, приложенного к пластинам А и В, возникают силы притяжения и вращающий момент, поворачивающий подвижную часть.
Если угол поворота а подвижной части прибора принять за обобщенную координату, то обобщенной силой будет вращающий момент:

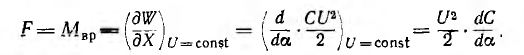
Спиральной пружиной D, осуществляющей электрический контакт с подвижной частью прибора, создается также противодействующий момент, пропорциональный углу поворота:

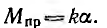
Под действием вращающего момента подвижные пластины будут поворачиваться до тех пор, пока этот момент не уравновесится противодействующим моментом пружины:

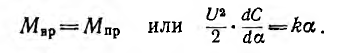
В измерительных приборах предпочтительна равномерная шкала, у которой а = k₁U, что приводит к уравнению

откуда получается необходимая зависимость емкости от угла поворота:

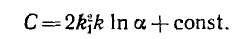
Придав соответствующие формы пластинам, удается получить равномерную
шкалу, за исключением ее начала, так как по мере приближения а к нулю |In а| стремится к бесконечности.

Замечательной особенностью электростатического вольтметра при постоянном
напряжении является отсутствие тока, потребляемого прибором в режиме установившегося отклонения.

Кроме вращающего и противодействующего моментов, во всех измерительных приборах создают момент успокоения М_усп. В электростатическом вольтметре используется магнитоиндукционный успокоитель (не показанный на рис. 2.4), состоящий из алюминиевой пластинки, закрепленной на оси прибора и расположенной в магнитном поле постоянного магнита. При движении подвижной части прибора в пластинке будут индуктироваться токи, тормозящие движение.

Таким образом успокаиваются колебания подвижной части прибора, что ускоряет получение установившегося отклонения; тогда M_усп = 0.

Емкостная машина постоянного тока

Машины, в которых производится прямое и обратное преобразование механической энергии в электрическую через посредство электрического поля, можно назвать емкостными, так как их работа основана на периодическом изменении взаимоемкости.

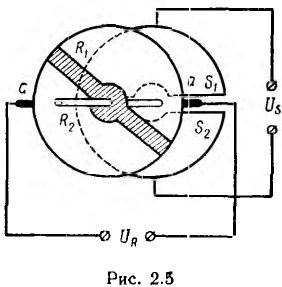
Емкостная машина постоянного тока (рис. 2.5) состоит из двух дисков: статора S_lS2 и ротора R₁R₂ вращающегося относительно статора. Каждый диск содержит два полудиска, изолированных друг от друга. Статорные полудиски образуют систему возбуждения. На роторные полудиски наложены щетки а, с помощью которых ротор подключается к сети при работе двигателем или к нагрузке при работе генератором. Напряжения U_s на статоре и U_r на роторе принимаются
постоянными.

Таким образом, емкостная машина состоит из двух конденсаторов R₁R₂ и S₁S₂ и подобна удвоенному электростатическому вольтметру, но без противодействующей пружины.

В соответствии с заряды роторного q_k и статорного q_s полудисков будут:

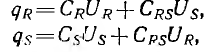
где C_R — собственная емкость ротора при накоротко замкнутых полудисках статора ;
C_s — собственная емкость статора при накоротко замкнутых полудисках ротора;
С_RS— взаимоемкость между статором и ротором.

Энергия электрического поля машины

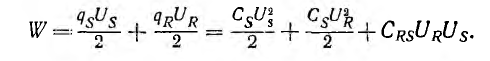
Пренебрегая влиянием изолирующего промежутка между полудисками, можно считать, что при вращении ротора емкости С_R и C_s остаются постоянными, а взаимоемкость C_RS будет периодически меняться. Поэтому появляющийся в машине вращающий момент

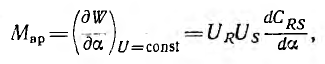
где a — угол поворота ротора.

В цепи ротора появляется ток

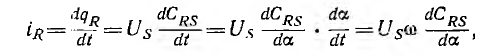
где 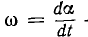— угловая скорость вращения.
Как видно из выражений для вращающего момента и индуктированного тока машины, они сохраняют постоянный знак только при сохранении знака производной 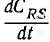. Для этого взаимоемкость должна непрерывно монотонно изменяться, что физически невозможно. В машине рис. 2.5 взаимоемкость изменяется от нуля до максимального значения и от максимального до нуля дважды за один оборот ротора. Для сохранения знаков вращающего момента и индуктированного тока необходимо использовать переключение — коммутацию, осуществляемую с помощью двух щеток а, скользящих по ободу
роторного диска и включенных в сеть.
Коммутация должна происходить при перемене знака производной 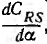, т. е. при переходе взаимоемкости через максимум, в момент совпадения положения полудисков ротора с полудисками статора.

При этом знак вращающего момента

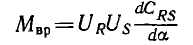
сохранится из-за одновременного изменения знака U_R, а ток ротора

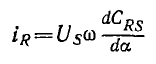
хотя и изменит свой знак внутри машины, но из-за переключения сохранит во внешней цепи свое направление.
Сказанное не противоречит установленному в п. 1 этого параграфа положению о невозможности непрерывного преобразования энергии электрического поля в механическую энергию в системе тел с постоянными потенциалами (напряжениями). Возбуждаясь от внешнего источника постоянного напряжения, такая машина благодаря коммутации представляет собой систему с переменным напряжением ротора.

Емкостная машина может работать как в генераторном, так и в двигательном режиме, но независимо от режима в ней всегда возникает вращающий момент и ток в цепи ротора.

В генераторе используется ток в цепи ротора. Проходя по нагрузке, он создает напряжение U_R ротора, которое вместе с напряжением U_$ создает вращающий момент. Этот момент в генераторе направлен против вращения, и его преодолевает первичный двигатель, вращающий генератор. Отдаваемая первичным двигателем механическая энергия преобразуется в генераторе в электрическую.

В двигателе, наоборот, используется вращающий момент, а ток, создаваемый машиной, преодолевается встречно направленным током сети и результирующий ток равен их разности. Электрическая энергия, отдаваемая сетью, преобразуется двигателем в механическую энергию.
Таким образом, емкостную машину постоянного тока независимо от того, будет ли она работать в режиме генератора или двигателя, осуществить без коммутации невозможно.

Движение заряженной частицы в электрическом поле

В современной технике широко применяется управление движущимися заряженными частицами с помощью электрического поля. Сюда относятся электронные и газоразрядные лампы, электронно-ионные приборы, электронные осциллографы, устройства для окраски в электрическом поле, для сепарации частиц электрическим полем и т. п.

Сила, действующая на частицу с зарядом Q, находящуюся в электрическом поле напряженности Е, равна

f = QE.

В соответствии с этим уравнения движения заряженной частицы с массой m имеют вид:

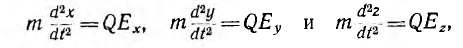
где E_x, E_y и Е_z — составляющие вектора напряженности поля по координатным осям XYZ.

Интегрирование этих уравнений при заданной напряженности поля как функции координат и заданных начальных условиях дает траекторию движущейся частицы.

В простейшем случае движения заряженной частицы вдоль однородного поля (Е_х = Е, Е_у = E_z = 0) при начальной скорости v₀, совпадающей по направлению с вектором Е, будет происходить вдоль оси X.
Тогда уравнение движения имеет вид:

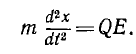
Интегрирование этого уравнения дает выражения:

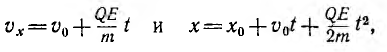
где х₀ — координата заряженной частицы в начальный момент времени.
Иными словами, заряженная частица движется вдоль однородного поля равноускоренно.

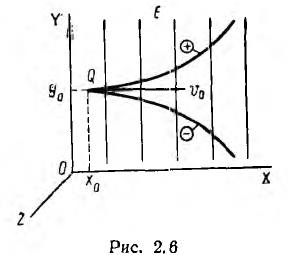
Если однородное поле направлено перпендикулярно в: направлению начальной скорости v₀ (рис. 2.6), как это имеет место, например, в электронном осциллографе с электрическим отклоняющим полем, то уравнения движения при Е_х — 0, Е_у = Е и Е_r = 0 будут:

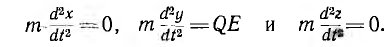
Их интегрирование дает

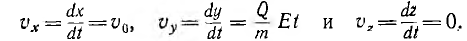
Таким образом, движение заряженной частицы совершается в координатной плоскости XOY. Вторичным интегрированием получаются уравнения траектории в параметрической форме, где у₀ — ордината частицы в начальный
момент:

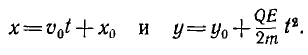
Исключение времени из этих уравнений дает уравнение траектории:

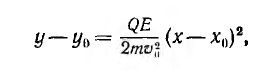
представляющее собой квадратичную параболу.

В электронном осциллографе движутся не положительно заряженные частицы, а электроны, что соответствует отклонению электронного луча не в направлении поля, а в обратном направлении, т. е. вниз на рис. 2.6.

Электронный осциллограф позволяет наблюдать и записывать на фотопленку кривые зависимости напряжения, подаваемого на отклоняющие пластины для создания электрического поля, от времени.

Основной особенностью электронного осциллографа является возможность использования его для исследования весьма быстро протекающих процессов, так как электронный луч практически безынерционен.

Энергия системы контуров с токами

Энергия линейной системы контуров с токами:

При создании магнитного поля током контура лишь часть работы, совершаемой внешними источниками, переходит в энергию магнитного поля; остальная часть расходуется на нагрев проводов, на излучение, на механическую работу, совершаемую силами поля. Уже созданное постоянное магнитное поле не требует затраты энергии для своего существования и энергия источника постоянного тока расходуется лишь на покрытие джоулевых потерь в контуре.

Пусть в системе n неподвижных контуров, находящихся в среде с постоянной магнитной проницаемостью, каждый контур питается от своего источника с постоянным напряжением U_k. Это напряжение в процессе установления тока и потокосцепления должно равняться сумме напряжения на сопротивлении R_k контура и напряжения, преодолевающего э. д. с. индукции

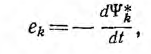
определяемой скоростью изменения потокосцепления 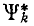контура:

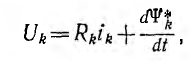
где 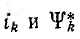— ток и потокосцепление контура k в процессе их установления до значений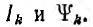

Тогда работа, совершаемая Ј-ым источником за бесконечно малое время dt, равна

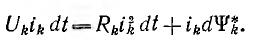
Второй член определяет потери энергии на джоулево тепло, третий — работу dA_k источника, идущую на изменение потокосцепления. Вся работа, затраченная на создание установившихся значений потокосцеплений во всех контурах системы,

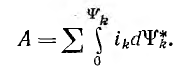
При достаточно медленном изменении токов можно пренебречь излучением и считать, что вся работа А равна энергии №, запасенной в системе контуров. Связь между токами и потокосцеплениями определяется как при постоянных токах:

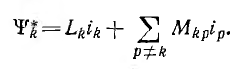
Согласно закону сохранения энергии, работа, затраченная на создание энергии системы, не зависит от порядка установления токов и потоков в контурах системы. Если для расчета выбрать порядок, когда токи всех контуров пропорциональны друг другу:

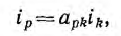
где a_Pk — постоянные, потокосцепление k-то контура будет равно

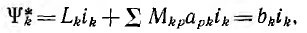
где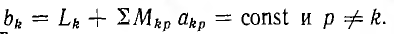

Тогда энергия системы

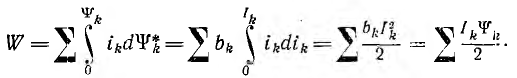
Для уединенного контура потокосцепление 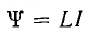и энергия

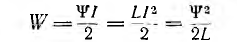
является квадратичной функцией тока или потокосцепления.

Энергия системы из двух контуров, связанных взаимной индукцией, потокосцепления которых определены,

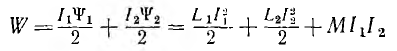
состоит из суммы собственных энергий каждого из контуров и взаим
ной энергии 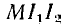зависящей от расположения контуров. В зависимости от направления токов в контурах член 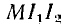может иметь разный знак, поэтому энергия системы будет больше суммы собственных энергий контуров при совпадении потоков само- и взаимоиндукции или меньше при встречном направлении потоков взаимоиндукции.

Однако суммарная энергия системы контуров с токами всегда положительна. Энергия системы нескольких контуров, состоящая из суммы собственных и взаимных энергий контуров,

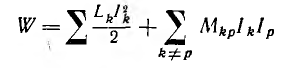
также всегда положительна.

Энергия нелинейного тороида

Аналогично энергии нелинейного конденсатора 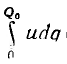  энергия тороида с сердечником из ферромагнитного материала, по обмотке которого проходит ток I₀,

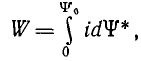
где i — устанавливающийся ток до значения I₀.
В зависимости от характера веберамперной характеристики эта энергия может быть меньше, равна или больше энергии 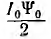линейного тороида с теми же конечными значениями тока 1₀ и потокосцепления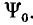
При периодическом изменении тока в обмотке нелинейного тороида от I₀ до —I₀ в нем проявляется магнитный гистерезис (см. рис. 1.19).

Если перемагничиваемый сердечник тороида имеет среднюю длину I и площадь поперечного сечения 5, то энергия, затраченная за один цикл перемагничивания, т.е. за один обход по петле гистерезиса, построенной в координатах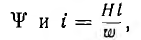

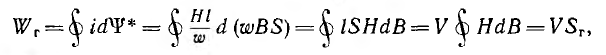
где V — SI — объем ферромагнетика;
S_r — площадь петли гистерезиса.

Так как эта площадь аналитически не вычисляется, то в технике пользуются приближенной формулой, установленной Штейнмецом экспериментальным путем:

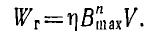
Коэффициент Штейнмеца η зависит от материала, показатель степени n — от материала и от величины максимальной индукции В_mах.
Для электротехнической стали при 0,25 < В_mах < 1 mл принимают n = 1,6, а при 1 < В_mах < 1,6 mл показатель степени n= 2.

Распределение анергии магнитного поля

Энергия магнитного поля распределена по всему объему, занимаемому полем.
Энергия тороида, имеющего w витков, длину средней линии I, площадь поперечного сечения S (см. рис. 1.14), если считать поле в сечении однородным, будет

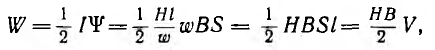
где V=SI — объем тороида и одновременно объем, занятый полем.

Тогда энергия на единицу объема — плотность энергии —

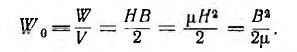
В случае неоднородного поля эти выражения могут быть использованы для бесконечно малого объема dV, в пределах которого поле может считаться однородным. Для конечного объема V энергия поля

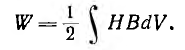
Эти формулы, выведенные для однородной изотропной среды, где векторы Н и В совпадают по направлению, могут быть записаны и так:

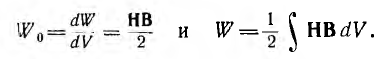
В таком виде выражение для энергии было постулировано Максвеллом для любых линейных и нелинейных сред и полей, как угодно изменяющихся во времени и в пространстве. Это обобщение, используемой теории электромагнитного поля, подтверждается совпадением выводов этой теории с опытом.

Взаимные преобразования энергии магнитного поля и механической энергии

Преобразование анергии и обобщенные силы:

В системе подвижных контуров с токами работа dA внешних источников равна сумме изменения энергии магнитного поля dW системы, механической работы dAMex и энергии потерь dA_n, преобразуемой в другие виды (тепловую и энергию излучения):

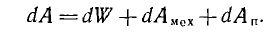
Если принять, что движение контуров и изменение токов происходит бесконечно медленно, то энергия dA_n будет содержать только тепловые потери dA_тепл. Так как механическая работа совершается за счет магнитного поля, создаваемого источниками, а доля работы источников

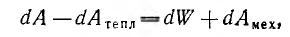
Пусть в системе контуров, описываемой с помощью обобщенных координат, возможно изменение лишь одной из них, например X, тогда механическая работа, совершаемая в системе, идущая на изменение поля, равна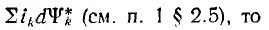

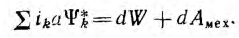
Пусть в системе контуров, описываемой с помощью обобщенных
координат, возможно изменение лишь одной из них, например X,
тогда механическая работа, совершаемая в системе,

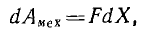
где F — обобщенная сила.
Исходное уравнение

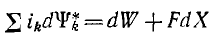
может быть исследовано лишь в двух частных случаях, рассматриваемых далее.
1. Если при изменениях, происходящих в системе, потокосцепления остаются постоянными 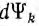= 0), исходное уравнение принимает вид:

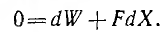
Источники не совершают работы, связанной с изменениями в системе, они покрывают лишь расход энергии на нагрев контуров.
В этом случае

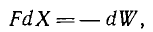
т. е. механическая работа совершается за счет убыли энергии системы.

Таким образом, при постоянных потокосцеплениях в системе она стремится под действием возникающих сил занять положение, соответствующее возможному в этой системе минимуму ее энергии.
2. Если источники поддерживают неизменными токи контуров (I_k = const), то дифференцирование выражения для энергии системы дает:

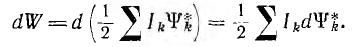
Тогда исходное равенство

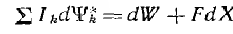
может быть приведено к виду:

откуда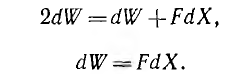

Это означает, что совершаемая системой механическая работа равна половине энергии, отдаваемой источниками; вторая половина идет на увеличение энергии системы.

Таким образом, система контуров с постоянными токами под действием возникающих в ней сил стремится занять положение, соответствующее возможному в этой системе максимуму ее энергии. Поскольку энергия при постоянных токах определяется величиной потокосцеплений, то система стремится занять положение, соответствующее максимуму потокосцеплений.

Так как в реальной системе может быть запасена лишь конечная энергия, то такая система при i_k = const также не может служить для непрерывного преобразования энергии магнитного поля в механическую.

Из приведенных соотношений могут быть вычислены обобщенные силы, действующие на контуры, находящиеся в магнитном поле. В случае постоянства потокосцеплений обобщенная сила

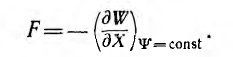
Здесь взята частная производная, так как рассматривается изменение энергии, соответствующее изменению лишь одной из обобщенных координат.
При постоянстве токов контуров выражение для обобщенной силы

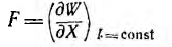
отличается от полученного выше. Однако результаты вычисления по этим формулам всегда совпадают, так как силы в системе в данный момент времени определяются значениями токов и потокосцеилений в этот момент времени
и не зависят от того, каким изменениям они будут подвергаться в дальнейшем.

Прибор электромагнитной системы

Примером одиночного контура с током может служить прибор электромагнитной системы (рис. 2.7), состоящий из неподвижной катушки А, в которую при прохождении по ней тока втягивается ферромагнитный сердечник В в виде фигурной пластинки, установленной на оси; на этой же оси укреплена стрелка С, перемещающаяся по шкале. Противодействующий
момент создается спиральной пружиной D.

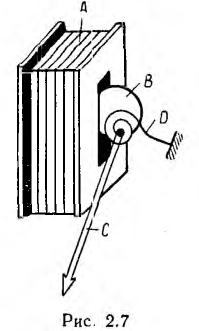
Успокоитель этого прибора — воздушный (на рис. 2.7 не показан). Он состоит из закрытой с одной стороны камеры, внутри которой может перемещаться легкий поршень, связанный с подвижной частью прибора. При ее повороте возникает разность давлений воздуха по обеим сторонам поршня, что оказывает тормозящее действие на колебания подвижной части и ускоряет получение установившегося отклонения; тогда момент успокоения М_усп = 0.

Если в качестве обобщенной координаты взять угол поворота а подвижной системы, то обобщенной силой будет вращающий момент

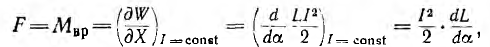
где L — индуктивность неподвижной обмотки, возрастающая при втягивании сердечника.
Уравнение равновесия подвижной части прибора — равенство вращающего и противодействующего моментов — имеет вид:

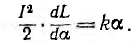
Требование равномерной шкалы а = k₁I приводит к уравнению:

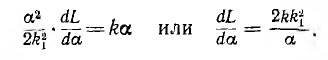
Следовательно, индуктивность должна изменяться в функции угла поворота по следующему закону:

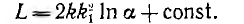
Путем придания сердечнику соответствующей формы удается получить равномерную шкалу, за исключением ее начала, так как по мере приближения а к нулю |In а| стремится к бесконечности.
Прибор электромагнитной системы может быть использован как амперметр, если его включить последовательно с приемником; тогда ток обмотки прибора равен измеряемому току. При использовании прибора в качестве вольтметра он включается параллельно приемнику; тогда ток обмотки и показания прибора пропорциональны измеряемому напряжению. При этом обмотка амперметра выполняется из относительно малого числа витков с сечением, рассчитанным на измеряемый ток, обмотка вольтметра — из большого числа витков малого сечения, рассчитанного на малый ток, обеспечивающий н. с. обмотки, равную н. с. обмотки амперметра.

Основным преимуществом прибора электромагнитной системы, наряду с простотой конструкции, является отсутствие токоподвода в подвижную часть.

Прибор электродинамической системы

Примером системы из двух контуров с токами является прибор электродинамической системы (рис. 2.8), состоящий из неподвижной катушки А и подвижной катушки В, укрепленной на оси, с которой скреплена стрелка С, перемещающаяся по шкале. Ток в подвижную катушку подводится через спиральные пружины D, служащие также для создания противодействующего момента. Успокоитель этого прибора — воздушный (см. п. 2 этого параграфа).

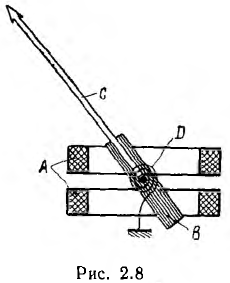
При повороте подвижной части индуктивности L₁ и L₂ обеих катушек остаются постоянными, а взаимоиндуктивность М изменяется. Если принять угол поворота а подвижной части прибора за обобщенную координату, то обобщенной силой будет вращающий момент

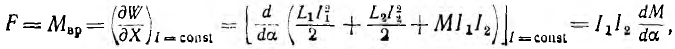
пропорциональный произведению токов обеих катушек. Он уравновешивается противодействующим моментом М_пр = ka. Прибор электродинамической системы может быть использован в качестве амперметра и вольтметра.

Например, в амперметре, предназначенном для измерения малых токов, неподвижная и подвижная катушки соединяются последовательно; тогда 1₁=I₂ =I и, следовательно,

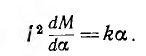
Требование равномерной шкалы для амперметра а = k₁l определяет зависимость взаимоиндуктивности М от угла поворота, выводимую из уравнения равновесия подвижной части прибора:

откуда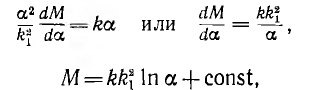

что невыполнимо в начале шкалы, так как |ln a |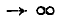 при а →0.

При использовании этого прибора в качестве вольтметра он включается параллельно нагрузке через добавочное сопротивление; тогда ток прибора пропорционален напряжению и его шкала также 1 не может быть выполнена равномерной.
Электродинамическая система используется также в ваттметрах; неподвижная
катушка включается последовательно с нагрузкой, и ее ток 1₁ равен току нагрузки I , а подвижная — параллельно приемнику, и ее ток I₂ пропорционален напряжению U цепи: 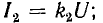тогда момент вращения будет пропорционален UI, т. е. мощности Р.

Требование равномерной шкалы для ваттметра a = k₁P приводит к уравнению

откуда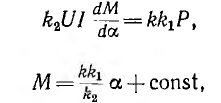

что выполнимо для всей шкалы.

Так как момент вращения амперметров и вольтметров электромагнитной и электродинамической систем пропорционален квадрату измеряемой величины, полярность их включения, т. е. направление тока в них, безразлична, но, как видно из выражения для момента вращения, его знак для ваттметра зависит от направлений токов в обеих катушках. Поэтому для получения положительного отклонения ваттметр должен включаться по схеме рис. 2.9, где точками отмечены условные «начала» катушек, указанные на приборе.

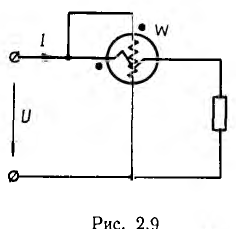
На рис. 2.9 для наглядности катушки ваттметра изображены с отступлением от ГОСТ 2. 729 - 68.

Индуктивная машина постоянного тока

В принципе обычная электрическая машина подобна рассмотренному в п. 3 этого параграфа прибору электродинамической системы, состоящему из неподвижной и подвижной катушек, но машина не имеет пружин, создающих противодействующий момент, и подвижная катушка (ротор) может вращаться. Так как процессы в этой системе вызваны изменением взаимоиндуктивности, такая машина может быть названа индуктивной.

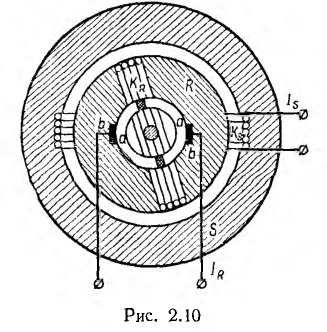
Индуктивная машина постоянного тока, принципиальное устройство которой показано на рис. 2. 10, имеет цилиндрические стальные магнитопроводы статора S и ротора R с минимальным зазором между ними, служащие для уменьшения магнитного сопротивления путей потока, благодаря чему увеличиваются потокосцепления при тех же токах.

Обмотка K_s образует поле возбуждения, обмотка ротора K_r подключена к сети или сопротивлению нагрузки. Если обмотки статора K_s и ротора K_r обтекаются постоянными токами I_s и I_r, потокосцепление обмотки ротора 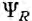и энергия W системы, соответственно, равны:

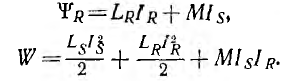
При вращении ротора индуктивности L_s и L_R обмоток статора и ротора, если пренебречь влиянием пазов, в которые уложены обмотки, остаются неизменными, а взаимоиндуктивность М между ними будет периодически меняться. Появляющийся в машине вращающий момент, равный производной энергии по углу а поворота ротора,

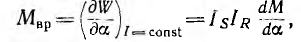
а э. д. с. индукции в обмотке ротора

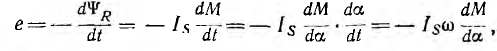
где 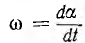— угловая скорость вращения.
Как видно из выражений для вращающего момента и э. д. с., они сохраняют постоянный знак только при сохранении знака производной 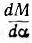. Для этого взаимоиндуктивность М должна непрерывно монотонно изменяться, что физически невозможно. В машине рис. 2.10 взаимоиндуктивность изменяется от нуля до максимального значения и от максимального значения до нуля дважды за один оборот ротора. Чтобы знаки вращающего момента и э. д. с. при этом не менялись, приходится применять переключение с помощью коммутатора, обычно выполняемого в виде коллектора. В машине рис. 2.10 он представляет собой соединенные с концами обмотки ротора два контактных
полукольца а, по которым скользят щетки b, приключенные к сети.

Коммутация должна происходить при перемене знака производной 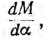т. е. при переходе взаимоиндуктивности через максимум в момент совпадения осей обмоток статора и ротора. Как видно из выражений для вращающего момента и э. д. с., момент сохранит свой знак благодаря одновременному изменению знака I_R, а изменившая свой знак э. д. с. оказывается переключенной и относительно зажимов сети также сохранит свой знак.

Работа такой машины не противоречит установленному выше положению о невозможности непрерывного преобразования энергии магнитного поля в механическую в системе контуров с постоянными токами, так как такая машина, питаясь постоянным током от внешнего источника, из-за коммутации представляет собой систему контуров с переменными токами.

В соответствии с принципом обратимости Ленца индуктивная машина может работать и генератором и двигателем, но независимо от режима работы в ней всегда возникают вращающий момент и э. д. с. индукции.
В генераторе используется э. д. с. машины, вызывающая при включении нагрузки ток I_R, который вместе с током I_S создает вращающий момент. Этот момент в генераторе направлен против направления вращения и его преодолевает первичный двигатель, вращающий генератор. Отдаваемая первичным двигателем механическая энергия преобразуется генератором в электрическую энергию.

В электрическом двигателе, наоборот, используется вращающий момент, а э. д.с. машины преодолевается встречно направленным напряжением источника. Электрическая энергия, поступающая от источника, преобразуется в механическую работу. Таким образом, индуктивная машина постоянного тока, независимо от того, работает ли она генератором или двигателем, без коммутации неосуществима.

Сравнение индуктивной и емкостной машин

В любой — индуктивной или емкостной — идеальной 'электрической машине без потерь при работе в двигательном режиме энергия W, запасенная в поле машины, полностью преобразуется в механическую работу за половину ее оборота. Тогда мощность машины

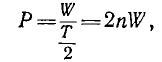
где Т — период вращения; п — число оборотов в единицу времени.

Это выражение из-за обратимости машин остается справедливым и для генераторного режима.

Обычно, сравнивая между собой емкостные и индуктивные машины, сопоставляют плотности энергии электрического и магнитного полей в зазоре машин, где сосредоточена основная доля энергии поля.

В емкостной машине удается достичь напряженности поля свыше 600 кв/см, что соответствует плотности энергии электрического поля

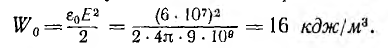
Плотность энергии магнитного поля при индукции В=1 mл

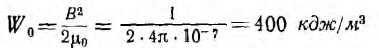
в 25 раз превышает плотность энергии в емкостной машине. На этом основании делают вывод о преимуществе индуктивных машин над емкостными.
Однако нужно сравнивать не плотности энергии магнитного и электрических полей в зазоре машин, а отношения энергии, запасенной в рабочем объеме машин, к объему всей машины.

В индуктивных машинах значительную часть их объема занимает ферромагнитный потокопровод, служащий для замыкания непрерывного магнитного потока. Поток же вектора смещения прерывен, начинаясь и кончаясь на заряженных проводниках. Поэтому емкостная машина не имеет потокопровода, и рабочий объем между взаимодействующими поверхностями составляет значительную долю всего объема машины. Таким образом, даже при меньшей плотности энергии электрического поля емкостная машина может не уступать индуктивной по величине энергии и мощности, приходящихся на единицу полного объема машины.

В отличие от индуктивных машин, являющихся машинами относительно невысокого напряжения и больших токов, емкостные машины — машины высокого напряжения (сотни и тысячи киловольт) и малых токов.
Индуктивные машины широко применяются во всех отраслях техники. Емкостные машины, получившие сравнительно узкую область применения, используются при исследовании атомного ядра, для окраски в электрическом поле, в электронно-ионной технике, для электросепарации и т. п.

Проводник с током в магнитном поле

Сила, действующая на проводник с током в магнитном поле:

Возникающие в системе контуров с токами силы нужно рассматривать как результат взаимодействия провода с током с магнитным полем других контуров. Это позволяет определить силы и в том случае, когда один из контуров в явном виде отсутствует, например в системах, содержащих постоянные магниты.

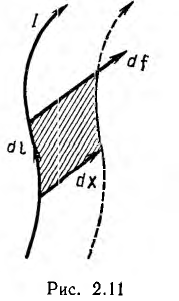
Пусть элемент dl провода, представляющего часть замкнутого контура с током I (рис. 2 .11), находится в магнитном поле с индукцией В. Под действием возникающей силы df элемент занял новое положение, переместившись на величину dx.
Тогда механическая работа

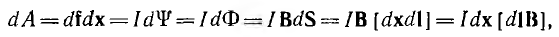
откуда сила, действующая на элемент длины dl провода с током,

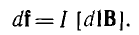
В соответствии с векторным произведением IdlB] направление силы связано с направлением тока (dl) и поля (В) правилом правого винта:
вращение правого винта от тока к полю (по меньшему углу) дает направление силы, совпадающее с направлением поступательного движения винта.
Для провода длиной I

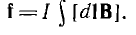
Если прямой провод длиной I находится в однородном поле, образуя угол а с направлением поля, то

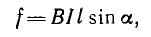
а в частном случае прямого провода, перпендикулярного направлению поля,

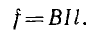
Следует помнить, что магнитное поле действует непосредственно на ток, а не на провод. Передача действия на провод осуществляется за счет связи свободных электронов с веществом провода. Поэтому это выражение для силы сохраняется и в случае, когда ток существует без провода, как, например, ток переноса.

Прибор магнитоэлектрической системы

В приборе магнитоэлектрической системы (рис. 2.12, ) легкая рамка А, представляющая собой катушку из w витков, находится в магнитном поле постоянного магнита М, снабженного полюсными наконечниками и сердечником из мягкой стали. При прохождении тока через рамку последняя поворачивается вместе с укрепленной на оси стрелкой С, конец которой перемещается по шкале. Противодействующий момент создается спиральными пружинами D, одновременно служащими токоподводами в подвижную рамку.

Для создания успокоения используется магнитоиндукционный принцип: катушка прибора намотана на алюминиевый каркас, в котором
во время поворота подвижной части магнитным полем магнита индуктируется ток, тормозящий движение.
Обычно в магнитоэлектрических приборах поле в воздушном зазоре радиально-однородно (рис. 2 . 12, б): в любом месте в пределах рабочей части индукция равна В.

В этом случае силы, действующие на рамку высотой I и шириной а,

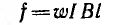
направлены всегда по касательной к окружности с диаметром а.
Вращающий момент, действующий на рамку,

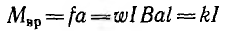
пропорционален току рамки. Следовательно, такой прибор при про
тиводействующем моменте М_пр= k₁a имеет равномерную шкалу.

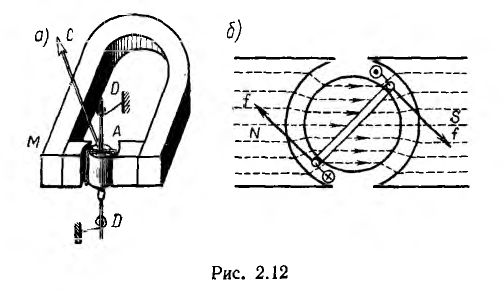
Магнитоэлектрический прибор также может быть использован в качестве амперметра или вольтметра.

Как видно из выражения для момента вращения, его знак зависит от направления тока в катушке. Поэтому на зажимах прибора показана его полярность, обеспечивающая отклонение подвижной части в нужную сторону.

Заряженная частица в магнитном поле

Сила, действующая на движущийся в магнитном поле заряд:

Пусть заряд dq движется в магнитном поле индукции В со скоростью 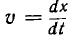в направлении оси х. Такой движущийся заряд эквивалентен току 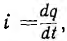текущему в том же направлении. На элемент длиной dx этого тока действует сила

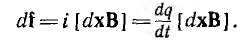
После введения dt под знак векторного произведения и замены 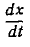скоростью v получается выражение для силы Лоренца:

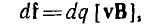
действующей на движущийся в магнитном поле заряд. Эта сила направлена перпендикулярно плоскости, в которой расположены векторы v и В. Так как на заряд может воздействовать только электрическое поле напряженностью Е, из сопоставления силы этого воздействия df = dqE с силой Лоренца di = dq [vB] видно, что в движущемся проводнике возникает электрическое поле напряженностью Е = [vB].

Из этого выражения видно, что на неподвижный (v=0) заряд или заряд, движущийся вдоль магнитного поля, оно не действует, так как при этом Е =[vB] = 0.

Направление вектора Е определяется правилом правого винта:
вращение винта от вектора скорости к вектору индукции дает направление электрического поля, совпадающее с направлением поступательного движения винта.
Следовательно, в проводнике возникает э. д. с.

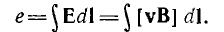
Это выражение является законом электромагнитной индукции в формулировке Фарадея.
В частном случае, широко используемом в технике, когда прямой
провод движется в однородном магнитном иоле перпендикулярно
полю и самому себе, э. д. с. в нем e = Blv.

Движение заряженной частицы в магнитном поле

Наряду с управлением движения заряженных частиц электрическим полем в электронно-ионной технике — электронных осциллографах, в ускорителях частиц, используемых при исследовании атомного ядра, фотоэлектронных умножителях и т. п. применяется также управление магнитным полем.
Если в магнитном поле с индукцией В иод действием силы Лоренца движется заряженная частица с массой m и зарядом Q, то ее уравнение движения имеет вид:

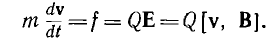
Раскладывая вектор скорости на две составляющие: v₁ параллельную вектору магнитной индукции, и 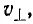перпендикулярную В, и учитывая, что 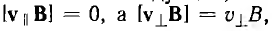можно получить из уравнения движения два уравнения:

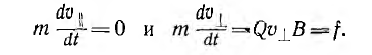
Первое уравнение, решением которого является v₁ = con‘t, описывает равномерное движение частицы, параллельное направлению вектора магнитной индукции В.

Из второго уравнения следует, что частица движется в плоскости,
перпендикулярной В, с постоянным ускорением

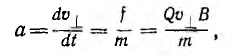
направленным, как и сила f, перпендикулярно составляющей скорости 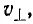. Как известно, такое движение есть равномерное движение по окружности, радиус которой

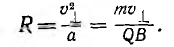
Таким образом, в однородном поле, когда величина и направление вектора магнитной индукции неизменны, заряженная частица движется по винтовой линии, расположенной по боковой поверхности прямого кругового цилиндра радиуса R.

Ось этого цилиндра совпадает по направлению с вектором В.В частном случае, когда 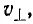= О, заряженная частица движется вдоль линии магнитной индукции — вдоль поля, причем последнее не оказывает никакого действия на движение частицы.

В неоднородном магнитном поле при движении заряженной частицы в направлении возрастания поля силовые линии будут сходящимися, и движение происходит по винтовой линии с уменьшающимся радиусом (рис. 2.13).

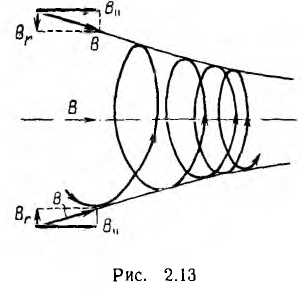
Вектор магнитной индукции В имеет, кроме продольной В₁ и, еще и поперечную составляющую В_г, направленную к оси винтовой линии. Эта составляющая вектора магнитной индукции создает силу, равную 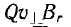и направленную против продольной составляющей скорости v₁. Под действием этой силы уменьшается расстояние между соседними витками траектории — шаг винтовой линии. Если составляющая скорости, обусловленная действием этой силы, превысит величину v₁, то частица, продолжая движение по винтовой линии, начнет двигаться в противоположном B₁ направлении с увеличением
радиуса R витков, сохраняя направление вращения.

Изучение движения заряженных частиц в магнитном поле представляет также интерес для теории северных сияний, магнитных бурь, поведения космических частиц в магнитном поле Земли и образования радиационных поясов Земли.