
Энергия магнитного поля
Содержание:
Энергия электрического и магнитного полей:
Электрическое и магнитное поля обладают энергией, которая накапливается при образовании заряда в электрической системе или образовании тока в электромагнитной системе. В данной главе получены количественные выражения энергии электрического и магнитного полей, а также электрических и электромагнитных сил.
Энергия электрического поля
При зарядке конденсатора энергия запасается в виде энергии электрического поля и может быть возвращена источнику при преобразовании в другой вид энергии.
Выражение энергии через характеристики конденсатора
Заряд конденсатора образуется переносом заряженных частиц с одной обкладки на другую под действием внешнего источника энергии. Работа, совершенная при переносе единицы заряда, численно равна напряжению между обкладками.
Если бы напряжение в процессе зарядки не изменялось, то энергию можно было бы определить произведением напряжения и заряда [см. формулу (1.5)]. Однако в процессе накопления заряда растет и напряжение, поэтому при определении энергии, затраченной на образование заряда, нужно учесть зависимость между напряжением и зарядом (7.28). Если емкость конденсатора — величина постоянная, зависимость между напряжением и зарядом графически выражается прямой линией (рис. 11.1).
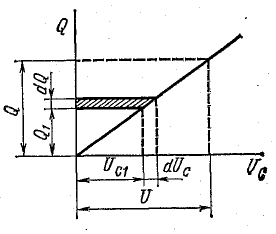
Рис. 11.1. К определению энергии электрического поля
Предположим, что заряд Q1 увеличился на dQ — величину столь малую, что в пределах изменения заряда напряжение можно считать неизменным: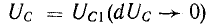
Выражение энергии через характеристики электрического поля
Выражение (11.2) получено на основе закона сохранения энергии; однако из него непосредственно не следует, что энергия Wэ является энергией электрического поля. Можно показать, что эта энергия распределена в электрическом поле.
Для примера рассмотрим равномерное электрическое поле плоского конденсатора (см. рис. 1.6, а).
Поток вектора электрического смещения через любую поверхность, проведенную в диэлектрике параллельно пластинам, равен заряду Q конденсатора, что следует из формулы (7.33): DS = Q.
Напряженность равномерного электрического поля Е = U/l.
Следовательно,
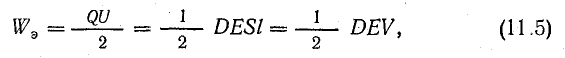
где V — объем диэлектрика, в котором распределено поле, связанное с заряженными пластинами конденсатора.
Отношение энергии к объему диэлектрика дает объемную плотность энергии электрического поля:
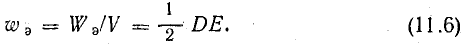
Энергия, определенная формулой (11.2) через характеристики проводников, выражена также формулой (11.5) через характеристики электрического поля. Эквивалентность этих формул свидетельствует о том, что энергия системы заряженных тел является энергией электрического поля.
Задача 11.1.
Плоский воздушный конденсатор емкостью 600 пФ при расстоянии между электродами 2 см заряжен до напряжения U = 4 кВ и отключен от источника напряжения. Определить изменение энергии и напряженности электрического поля конденсатора при уменьшении расстояния между электродами вдвое.
Решение. До изменения расстояния между обкладками энергия электрического поля, по формуле (11.3),
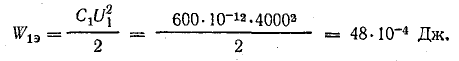
Напряженность электрического поля [см. (1.5)]
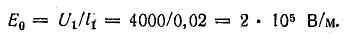
При уменьшении расстояния между обкладками вдвое емкость конденсатора согласно формуле (7.29) увеличивается вдвое. При этом заряд конденсатора не изменяется (предполагается, что утечки заряда нет).
Вследствие увеличения емкости конденсатора напряжение между обкладками уменьшится во столько же раз [см. формулу (7.28)]:
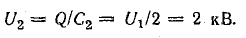
Энергия электрического поля
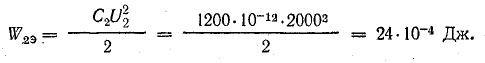
Напряженность электрического поля
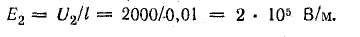
Механические силы в электрическом поле
Вопрос о механических силах в электрическом поле рассмотрим на примере плоского конденсатора, заряженного от внешнего источника энергии, имеющего напряжение U. Электрическое поле конденсатора будем полагать равномерным.
Энергетический баланс в электростатической системе
Силы Fэ, возникающие вследствие взаимодействия пластин с электрическим полем, приложены к пластинам и направлены так, что они притягиваются. Предположим, что одна из пластин конденсатора свободна, и возможное малое перемещение ее под действием силы Fэ обозначим через dх (рис. 11.2).
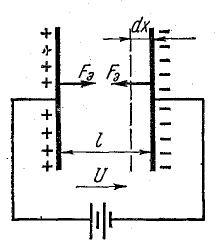
Рис. 11.2. Механические силы в электрическом поле
В дальнейших рассуждениях будем исходить из того, что при изменении заряда конденсатора не возникает потерь энергии в проводниках в связи с перемещением заряженных частиц и в диэлектрике вследствие изменения напряженности поля.
При таких условиях в соответствии с законом сохранения энергии при изменении заряда конденсатора на dQ за счет энергии внешнего источника изменяется энергия электрического поля на dWэ и совершается механическая работа Fэdx:
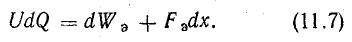
Обобщенное выражение электрической силы (первый случай)
Заряд конденсатора остается неизменным (Q = const), т. е. заряженный конденсатор отключен от внешнего источника энергии.
При dQ = 0 работа внешнего источника UdQ = 0. Поэтому
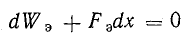 или
или 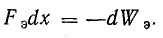
Последнее равенство показывает, что механическая работа, связанная с перемещением пластины, совершается за счет энергии электрического поля.
Действительно, механическая работа, совершаемая электрической силой, положительна (Fэdх > 0), следовательно, изменение энергии электрического поля отрицательно (dWэ < 0). Это значит, что энергия электрического поля в данном случае уменьшается.
Механическую силу, стремящуюся изменить положение пластины конденсатора, можно выразить отношением
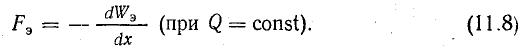
Рассуждая аналогично, можно получить зависимость между механическим моментом и углом поворота α, если механическое движение осуществляется в виде вращения одной пластины по отношению к другой:

Изменение расстояния l между пластинами на dх изменит емкость конденсатора. При уменьшении расстояния емкость увеличивается, а напряжение между пластинами уменьшается, что непосредственно следует из формулы (7.28).
Предположим, что расстояние между пластинами увеличивается благодаря действию на пластины внешних механических сил. Энергия в системе возрастает на величину работы, совершенной внешним источником механической энергии. При этом емкость конденсатора уменьшится, а напряжение между пластинами увеличится.
Обобщенное выражение электрической силы (второй случай)
Напряжение между пластинами остается постоянным (U = const), т. е. во время движения пластины конденсатор не отключается от внешнего источника энергии.
При уменьшении расстояния между пластинами увеличивается емкость конденсатора, что при неизменном напряжении влечет за собой увеличение заряда.
Внешний источник энергии должен затратить энергию на увеличение заряда конденсатора в количестве UdQ.
Изменение энергии электрического поля dWэ при изменении заряда, согласно формуле (11.2), 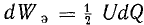 , т. е. составляет половину энергии внешнего источника, израсходованной при увеличении заряда конденсатора. Вторая половина энергии расходуется на покрытие механической работы Fэdх, следовательно,
, т. е. составляет половину энергии внешнего источника, израсходованной при увеличении заряда конденсатора. Вторая половина энергии расходуется на покрытие механической работы Fэdх, следовательно,
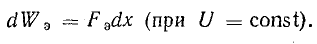
Отсюда

Аналогично, при вращательном движении

Увеличение расстояния между пластинами в результате действия внешних механических сил приведет к уменьшению емкости. Но при постоянном напряжении за уменьшением емкости последуют уменьшение заряда конденсатора и уменьшение энергии электрического поля. В этом случае механическая работа, связанная с перемещением пластины, совершается внешними механическими силами. Величина этой работы численно равна уменьшению энергии электрического поля. Таким образом, источнику электрической энергии возвращается энергия, численно равная удвоенному значению механической работы.
Энергия магнитного поля
При возникновении электрического тока в проводящем контуре одна часть энергии источника питания расходуется на преодоление электрического сопротивления контура и превращается в тепло, а другая запасается в виде энергии магнитного поля.
Энергия магнитного поля уединенного контура или катушки с током
Определим вначале энергию магнитного поля уединенного контура с током I, пользуясь формулой (8.21), согласно которой изменение энергии в магнитной системе связано с изменением потокосцепления.
При этом нужно принять во внимание, что в процессе возникновения тока в контуре его величина не остается постоянной, а увеличивается от 0 до I. Вместе с изменением тока изменяется и потокосцепление [см. формулу (8.23)].
При таких условиях оба множителя в формуле (8.21) являются переменными, поэтому при помощи этой формулы можно определить лишь приращение энергии dWм за некоторый весьма малый промежуток времени, в течение которого ток в контуре можно считать неизменным:

где i — некоторое промежуточное значение тока между 0 и I, принятое неизменным в течение бесконечно малого промежутка времени; dψ —приращение потокосцепления за тот же промежуток времени.
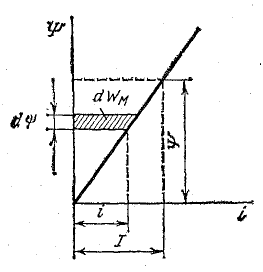
Рис. 11.3. К определению энергии магнитного поля
Если индуктивность контура постоянна, то зависимость между потокосцеплением и током графически изображается прямой линией (рис. 11.3). Изменение энергии при токе i выразится заштрихованным элементом площади [см. формулу (11.12)]. Энергию при потокосцеплении ψ и токе I можно определить суммой таких элементов, т. е. площадью прямоугольного треугольника с катетами ψ и I:
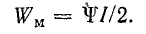
Учитывая формулу (8.23), запишем и другие выражения для определения энергии магнитного поля:
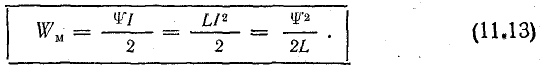
Энергия магнитного поля в системе магнитно-связанных контуров (катушек)
Определим энергию магнитного поля в системе двух магнитно-связанных контуров (катушек) с токами.
Энергия магнитного поля этой системы накапливается в процессе установления токов в обоих контурах, причем в процессе накопления определенное влияние оказывает взаимное потокосцепление.
По закону сохранения энергии, общий запас энергии в магнитном поле не зависит от последовательности установления тока в контурах.
Учитывая это, зададим определенную последовательность установления токов в контурах: сначала ток увеличивается от 0 до I1 в первом контуре, а после этого — от 0 до I2 во втором контуре.
При изменении тока в первом контуре изменяется собственное потокосцепление первого контура от 0 до ψ1.1 и взаимное потокосцепление второго контура от 0 до ψ1.2.
Энергия в системе определяется только изменением собственного потокосцепления и при установившемся токе I1 выражается формулой (11.13):
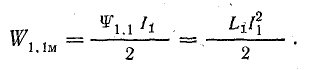
Энергия, определяемая изменением взаимного потокосцепления, равна нулю, так как во втором контуре ток равен нулю.
При изменении тока во втором контуре изменяются собственное потокосцепление второго контура от 0 до ψ2.2 и взаимное потокосцепление первого контура от 0 до ψ2.1.
Взаимное потокосцепление второго контура при этом не изменяется, так как ток в первом контуре уже установился.
К запасу энергии W1.1м добавляются энергия, определяемая изменением собственного потокосцепления второго контура:
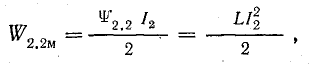
н энергия, определяемая изменением взаимного потокосцепления первого контура:
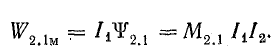
Последняя часть энергии выражена по формуле (8.21), так как магнитное поле второго контура взаимодействует с постоянным током первого контура.
Энергия магнитного поля системы двух контуров с токами
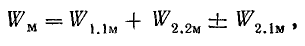
или
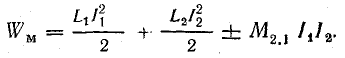
Учитывая независимость энергии магнитного поля от последовательности установления токов в контурах или принимая во внимание, что М2.1 = М1.2 = М, получим окончательно
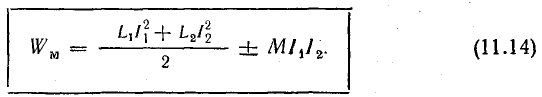
Знак перед выражением МI1I2 в уравнении (11.14) зависит от способа включения контуров (катушек).
При согласном включении взаимное потокосцепление совпадает по направлению с собственным, поэтому энергия взаимосвязи входит в уравнение со знаком плюс. При встречном включении взаимное потокосцепление направлено против собственного, поэтому энергию взаимосвязи в той же формуле нужно взять со знаком минус.
Индуктивность в системе магнитно-связанных катушек
Рассмотрим частный случай, когда две магнитно-связанные катушки электрически соединены между собой последовательно, в результате чего в обеих катушках ток I один и тот же (см. рис. 8.22).
Энергия магнитного поля такой системы
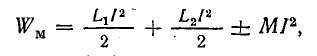
или
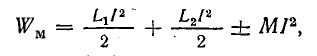
где 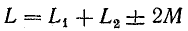 — индуктивность системы магнитно-связанных катушек.
— индуктивность системы магнитно-связанных катушек.
При согласном включении
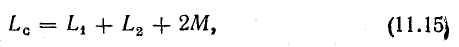
при встречном включении
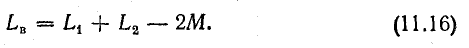
Выражение энергии через характеристики магнитного поля
Формулами (11.13) и (11.14) энергия выражена через характеристики контуров с токами.
Можно показать, что в данном случае энергия распределена в магнитном поле, окружающем проводники с токами.
Для примера возьмем поле катушки с кольцевым сердечником. Если диаметр сечения сердечника много меньше диаметра самого сердечника, поле можно считать равномерным:
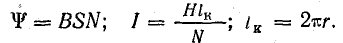
Тогда
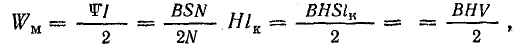
где 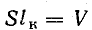 — объем сердечника.
— объем сердечника.
Энергия магнитного поля в единице объема

Здесь энергия выражена через характеристики магнитного поля, что свидетельствует о ее принадлежности магнитному полю.
Задача 11.8.
Определить энергию магнитного поля в системе двух обмоток (задача 8.21) при согласном и встречном их включении, если ток в первой обмотке I1 = 5 А, а во второй I2 = З А.
Решение. Для определения энергии в магнитно-связанной системе двух обмоток воспользуемся формулой (11.14).
Величины индуктивностей катушек и взаимной индуктивности при неферромагнитном сердечнике не зависят от тока в них, поэтому возьмем их по результатам решения задачи 8.21:
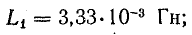
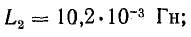
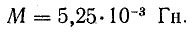
При согласном включении обмоток
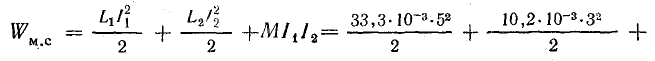
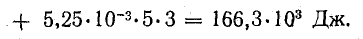
При встречном включении
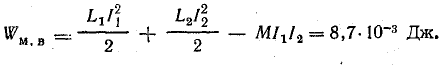
Задача 11.9.
Общая индуктивность двух последовательно соединенных катушек (см. рис. 8.22) при согласном включении равна 1,52 мГн, при встречном — 0,88 мГн. Определить взаимную индуктивность катушек.
Решение. Найдем взаимоиндуктивность катушек, решив совместно уравнения (11.15) и (11.16):
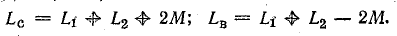
Вычтем второе уравнение из первого:
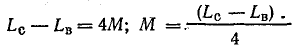 .
.
В данном случае 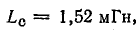
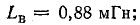
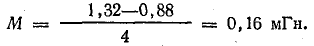
Механические силы в магнитном поле
В технике широко применяются устройства, в основе работы которых лежит силовое действие магнитного поля (электродвигатели, реле, тяговые и подъемные электромагниты, электроизмерительные приборы и др.).
Электромагнитные силы приходится учитывать при расчете электрических аппаратов, проектировании распределительных устройств электростанций и в других случаях.
Энергетический баланс в электромагнитной системе
Определение электромагнитной силы Fм рассмотрим на примере взаимодействия полюсов электромагнита (рис. 11.4), полагая магнитное поле в воздушном зазоре между полюсами равномерным.
Обозначим ток в обмотке электромагнита через i, сопротивление обмотки — R, возможное малое перемещение одного из полюсов (якоря электромагнита) — dх.
Работа внешнего источника энергии, к зажимам которого подключена обмотка электромагнита, в общем случае расходуется на выделение тепла в обмотке (i2Rdt), на изменение энергии в магнитном поле (dWм) и механическую работу (Fмdх).
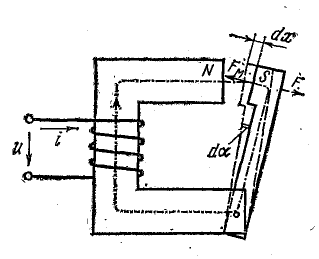
Рис. 11.4. Взаимодействие полюсов электромагнита
Согласно закону сохранения энергии, за малый отрезок времени энергетический баланс в системе выражается уравнением
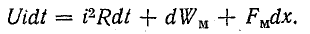
Два последних слагаемых в правой части уравнения выражают изменение энергии в магнитной системе. Рассмотрим их более подробно. При этом учтем выводы о том, что изменение энергии магнитного поля и работа электромагнитных сил определяются изменением потокосцепления:
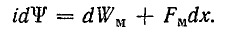
Обобщенное выражение электромагнитной силы (первый случай)
Потокосцепление в магнитной системе не изменяется (ψ = const, dψ = 0); это условие обычно соблюдается в электромагнитах переменного тока. Тогда
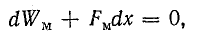
а
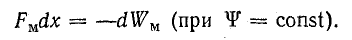
Последнее равенство показывает, что механическая работа, связанная с перемещением якоря электромагнита, совершается за счет энергии магнитного поля. Внешний источник расходует энергию только на выделение тепла.
Механическая работа электромагнитной силы положительна (Fмdx > 0); следовательно, изменение энергии магнитного поля отрицательно (dWм < 0), т. е. она убывает.
Механическая сила, стремящаяся изменить положение якоря, может быть выражена отношением

Аналогично можно получить зависимость между механическим моментом и углом поворота якоря:

Обобщенное выражение электромагнитной силы (второй случай)
Ток в обмотке электромагнита поддерживается постоянный (i = const). При уменьшении расстояния между полюсами увеличивается индуктивность, что при неизменном токе повлечет за собой увеличение потокосцепления. Внешний источник должен затратить энергию на увеличение потокосцепления в количестве idψ.
Согласно формуле (11.13), энергия магнитного поля изменяется на величину
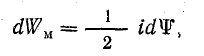
что составляет половину энергии внешнего источника, а другая расходуется на покрытие механической работы Fмdx.
Следовательно,
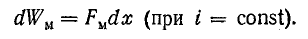
Отсюда

Аналогично, для вращательного движения

Таким образом, механическая сила (или момент), стремящаяся изменить положение якоря электромагнита, равна увеличению энергии магнитного поля в расчете на единицу изменения пути (или угла), если ток в обмотке не изменяется.
Увеличение воздушного зазора в результате действия внешней механической силы приведет к уменьшению индуктивности. Но при неизменном токе за этим последует уменьшение потокосцепления и энергии магнитного поля.
Механическая работа, связанная с перемещением якоря, совершается внешними механическими силами. Величина этой работы численно равна уменьшению энергии магнитного поля. Таким образом, источнику электрической энергии возвращается энергия, численно равная удвоенной величине механической работы.
Используя общие выводы и формулы, полученные ранее, найдем выражения для определения электромагнитных сил в конкретных случаях, встречающихся на практике.
Тяговое усилие электромагнита
Отрывная сила (груза, пружины и т. д.) стремится увеличить воздушный зазор между полюсами электромагнита. Предположим, что этот зазор увеличится на dx. При этом объем, в котором распределено магнитное поле, увеличится на (dV = Sdx, где S — площадь полюса.
Изменение энергии магнитного поля составит
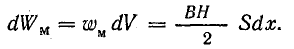
Согласно формуле (11.20),
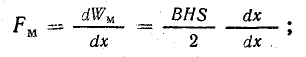
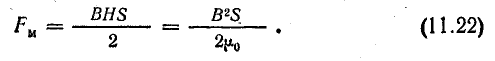
Силы взаимодействия двух параллельных проводов с токами
На практике часто встречается параллельное расположение проводов с токами. Таким образом, например, монтируются шины распределительных устройств электрических станций и подстанций. Для того чтобы правильно выбрать шины и изоляторы, на которых они закреплены, необходимо определить электромагнитные силы взаимодействия между шинами.
В данном случае силу взаимодействия можно рассматривать как действие магнитного поля тока первого провода I на ток второго II, или наоборот (рис. 11.5).
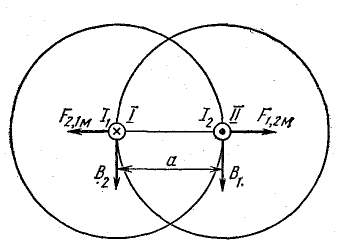
Рис. 11.5. К определению сил взаимодействия двух параллельных проводов
Согласно формуле (8.10), магнитное поле тока первого провода в месте расположения второго провода характеризуется индукцией
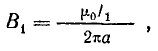
где а — расстояние между осями проводов.
Между направлениями В1 и I2 угол α = 90°.
По формуле (8.4), сила, действующая на ток второго провода в поле первого провода,
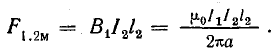
Аналогичное выражение получается для силы, действующей на ток первого провода в магнитном поле тока второго провода:
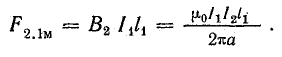
Рассматривая взаимодействие равных участков l двух проводов, получим общую формулу

Действие магнитного поля на свободно заряженную частицу
Действие магнитного поля на заряженные частицы, движущиеся вне проводника, например в вакууме, широко используется в технике.
Примерами такого использования могут служить: фокусировка или смещение электронного пучка (луча) в электроннолучевых трубках телевизора и осциллографов или электронных микроскопах, ускорение заряженных частиц для исследования ядерных процессов и т. д.
Для определения силы, которая действует на частицу с зарядом Q, движущуюся в равномерном магнитном поле, можно использовать формулу (8.5), подставив в нее 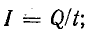
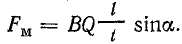
Рассматривая длину проводника l как путь, пройденный заряженной частицей за время t, отношение l/t можно считать скоростью движения частицы
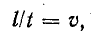
тогда

где α — угол между направлениями линий магнитной индукции и направлением движения заряженной частицы. При а α= 90º

Сила Fм, согласно правилу левой руки, направлена перпендикулярно направлению линий магнитной индукции и направлению скорости.
Из механики известно, что при действии на тело постоянной по величине силы перпендикулярно направлению скорости тело движется по окружности радиуса
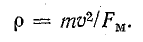
Подставляя в последнее выражение силу из формулы (11.25), получим

где m — масса заряженной частицы.
Если все величины правой части уравнения (11.26) постоянны, то заряженная частица движется по окружности радиуса ρ в плоскости, перпендикулярной направлению линий магнитной индукции. Угловая скорость движения

Задача 11.11.
В вершинах А, В, С равностороннего треугольника со стороной а = 10 см расположены три параллельных прямых провода (рис. 11.6). Токи в проводах В и С равны по величине: IB = IC = 6000 А и направлены в одну сторону, а ток в третьем проводе IA = 12 000 А направлен в противоположную сторону. Определить силу, действующую на 1 м длины каждого провода.
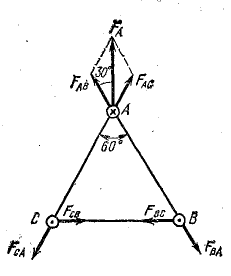
Рис. 11.6. К задаче 11.11
Решение. Рассматривая отдельно каждую пару проводов, определим направление сил взаимодействия между ними. При этом будем иметь в виду, что при одинаковом направлении токов провода притягиваются друг к другу, а при разном — отталкиваются. Направления сил показаны на рис. 11.6. Величину их определим по формуле (11.23):
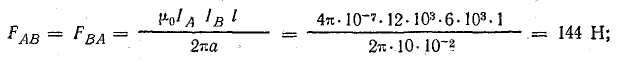
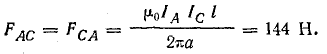
Величину и направление силы FA, действующей на провод А, определяют векторным сложением составляющих: 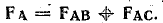 В данном случае складываются две равные силы с углом 60° между их направлениями.
В данном случае складываются две равные силы с углом 60° между их направлениями.
Результирующая сила направлена посредине между составляющими и имеет величину 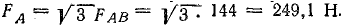
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
- Резонанс в электрических цепях
- Соединение звездой и треугольником в трехфазных цепях
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Электрическое поле и его расчёт
- Расчет неразветвленной однородной магнитной цепи